舵机驱动的足式机器人腿部运动性能优化策略
2015-08-10邓学磊杨灿军范锦昌尚伟燕
邓学磊,杨灿军,毕 千,范锦昌,尚伟燕
(浙江大学 流体动力与机电系统国家重点实验室,浙江 杭州310027)
随着我国科学的快速发展以及资源的日渐匮乏,面向海洋的开发已经成为我国21世纪最重要的方向.面对水下极端、复杂的环境,大深度、大范围和高危险的资源考察和开发任务,水下机器人受到广泛关注.本文旨在减小水下足式爬壁机器人步态控制误差.
国内外对足式机器人的研究很多,其中美国Case Western Reserve University(CWRU)大学研制的Robot系列机器人有一定的代表意义.他们对每一代的驱动方式都作出了很大的改进,从最简单的舵机驱动到复杂的仿生肌肉驱动都进行了尝试[1-2].国内,王倩等[3]研制出六足机器人HIT-Spi-der,每条腿拥有3 个自由度,由舵机驱动.由此可见,舵机是一种简单易行的机器人控制方法.
本文的研究对象是一个四足机器人,每条腿拥有4个自由度,由舵机驱动.该机器人在控制方面主要有以下几个问题.
1)与小型爬行仿生机器人不同,该机器人需要在水下极端环境中工作,并带有一定负载,需要较大的驱动力.
2)为了对抗海浪等外界干扰,机器人的整体设计重量较大.
3)在实际工作过程中,机器人可能在重力方向上爬行,故机器人自重是一个重要的负载,这要求机器人腿部足够强壮,不能像传统仿生机器人一样,将重量集中在机身.
4)在舵机控制中一般采用开环的控制方法.
5)舵机在运行的过程中会受到摩擦力以及齿轮间隙的因素的影响.
这些问题的共同影响会导致舵机运行轨迹与理想轨迹之间产生误差,并会表现出一些非线性的现象.针对这些问题,国内外的学者提出了很多解决方案.
林忠万等[4-6]在舵机外加入传感器,构成闭环系统,采用传统PID 方法和分形修正PID 算法对舵机进行控制,用反馈信号短时分形维数估计舵机实际转角与电机驱动力之间的相背离程度,利用该估计函数修正PID 输出值.刘兴中等[7]利用了更简单的PI调节器,达到了不错的效果.李全福等[8-9]采用模糊PID 算法,明显改善了系统的动态特性,并最终得出结论:可以利用模糊PID 混合控制改善控制系统的动态性能,同时利用常规PID 改善模糊控制的稳态性能.近几年,胡林等[10-11]提出加入鲁棒控制,得到了不错的效果.这些研究工作均建立在加入传感器,并将控制系统变为闭环系统后的基础上,并且这些算法较复杂.
为了令机器人结构更加轻便,控制算法更加精简,本文旨在不加入传感器的基础上,利用前馈补偿,达到减小控制误差的目的.本文方法的优点在于,在水下极端环境下,过多的设备不仅会增加机器人的负担,也有可能因为工作环境成为机器人不稳定的因素.本文以单腿为例,首先对单腿进行运动学分析,仿真出理想运动轨迹;然后通过实验检测出实际运行轨迹与理想轨迹之间的误差,通过数学表达式描述其非线性特性;最终通过增加前馈补偿的方法,减小其控制中的误差.
1 运动学分析与仿真
1.1 运动学正解
受控对象如图1所示,为四自由度腿部结构,其中髋关节二自由度,膝关节、踝关节各一个自由度.建立如图1所示的D-H 坐标[12-13],其中各关节参数如表1所示.
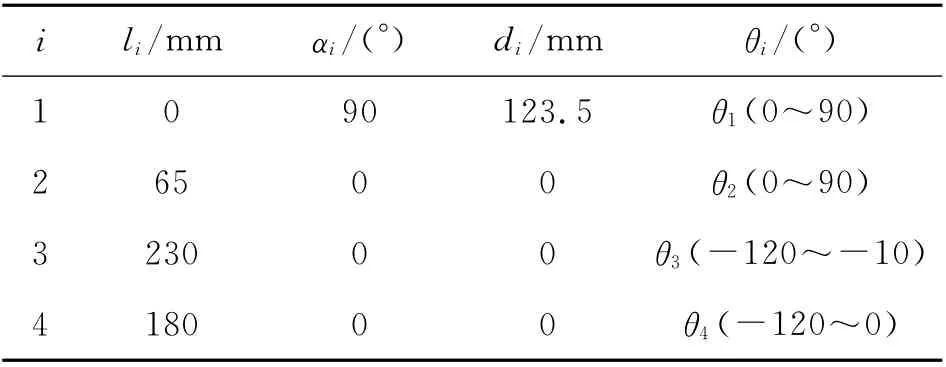
表1 D-H 坐标参数Tab.1 D-H parameters
根据建立的D-H 坐标,对机器人进行运动学求解,得到单腿变换矩阵为

式中:
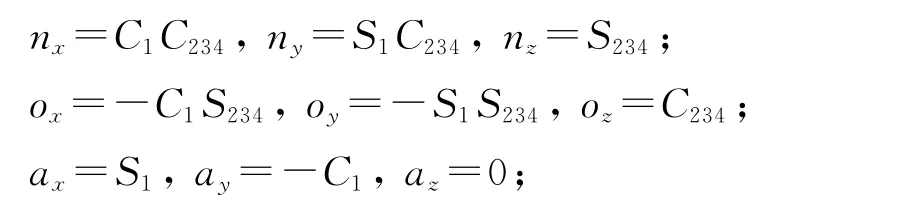
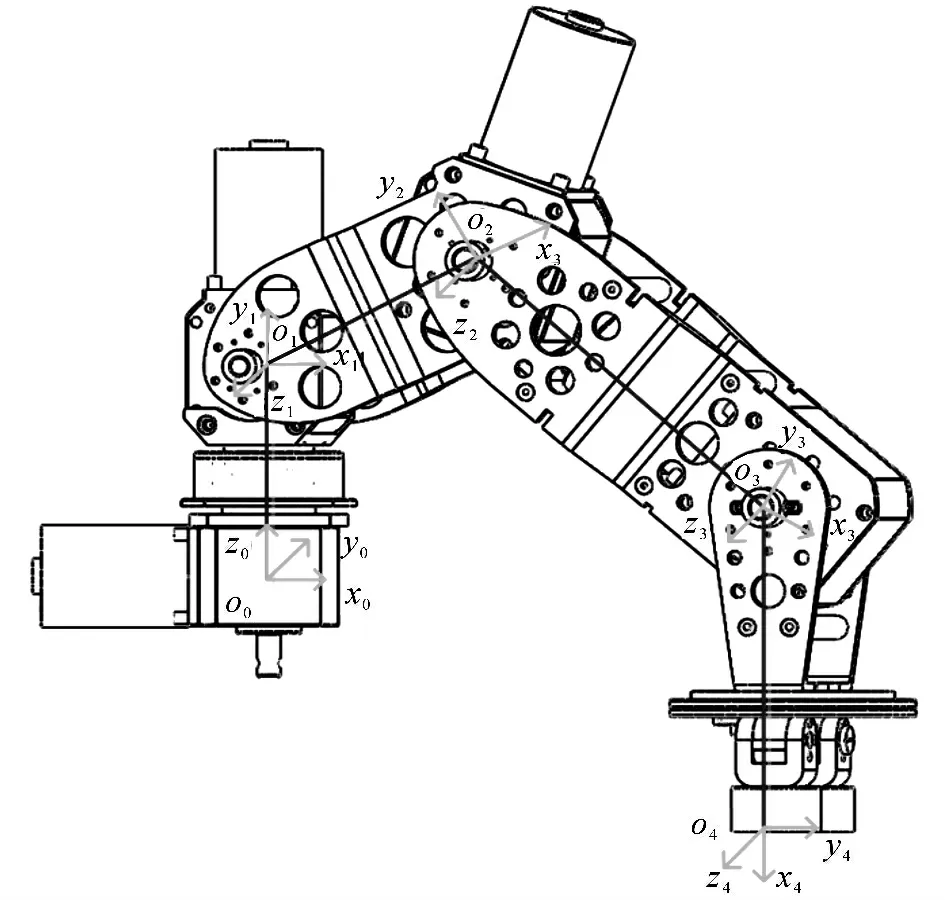
图1 机器人D-H 坐标建立Fig.1 Establishment of D-H coordinate
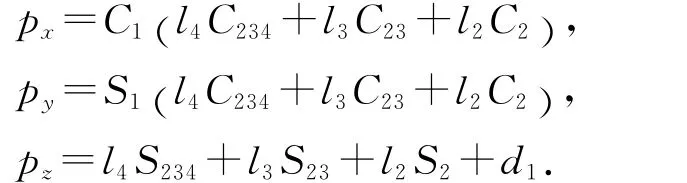
1.2 运动学逆解
在爬行过程中,足底需要进行吸附,需要腿部最后关节与地面始终垂直,得到限定条件θ1+θ2+θ3=-90°.可以逆解出各个关节角度:
式中:
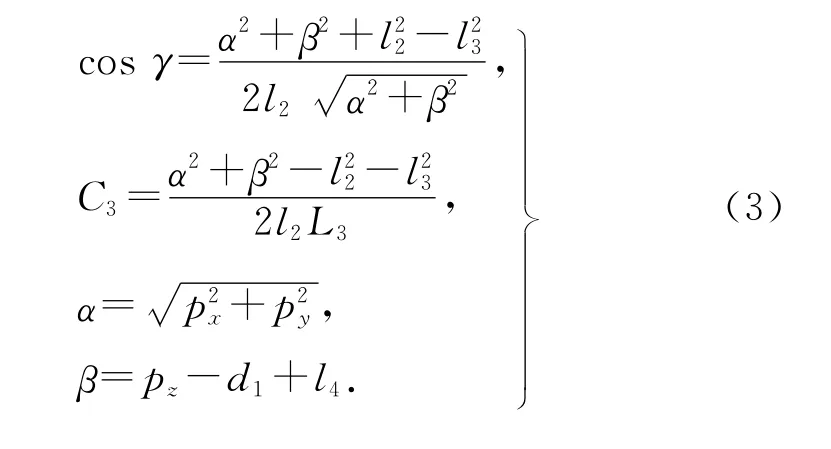
2 运动控制误差
首先将前文计算的各关节角度作为输入量来验证运动学分析的正确性.在进行实验之前,已对舵机进行标定,消除了由于安装造成的基础误差以及可能由舵机内部电路产生的线性误差.
通过摄像系统对受控对象进行精确测量,将摄像头分布在一个球面上,可以有效地提高采集及标定精度,如图2(a)所示.同时,在每个关节以及足底附近位置上粘贴了标记点,便于摄像系统采集关节位置,如图2(b)所示.
通过采集数据的分析处理得到各关节角度,如图3所示.通过计算得到各个关节的平均相对误差均在5%以内,但是由于关节机器人每个关节误差的累积,导致足底末端的轨迹与理想轨迹产生了较大的误差.
3 误差消除策略
为了消除足底末端位置的误差,提高各个关节的控制精度.为了使机器人结构更加轻便,以适应水下极端的工作环境,本文未对各关节舵机加入传感器构成反馈,采用前馈补偿的方式,对误差进行估计,并加以消除.

图2 水下足式机器人实验装置Fig.2 Experiment equipment of underwater multi-legged robot
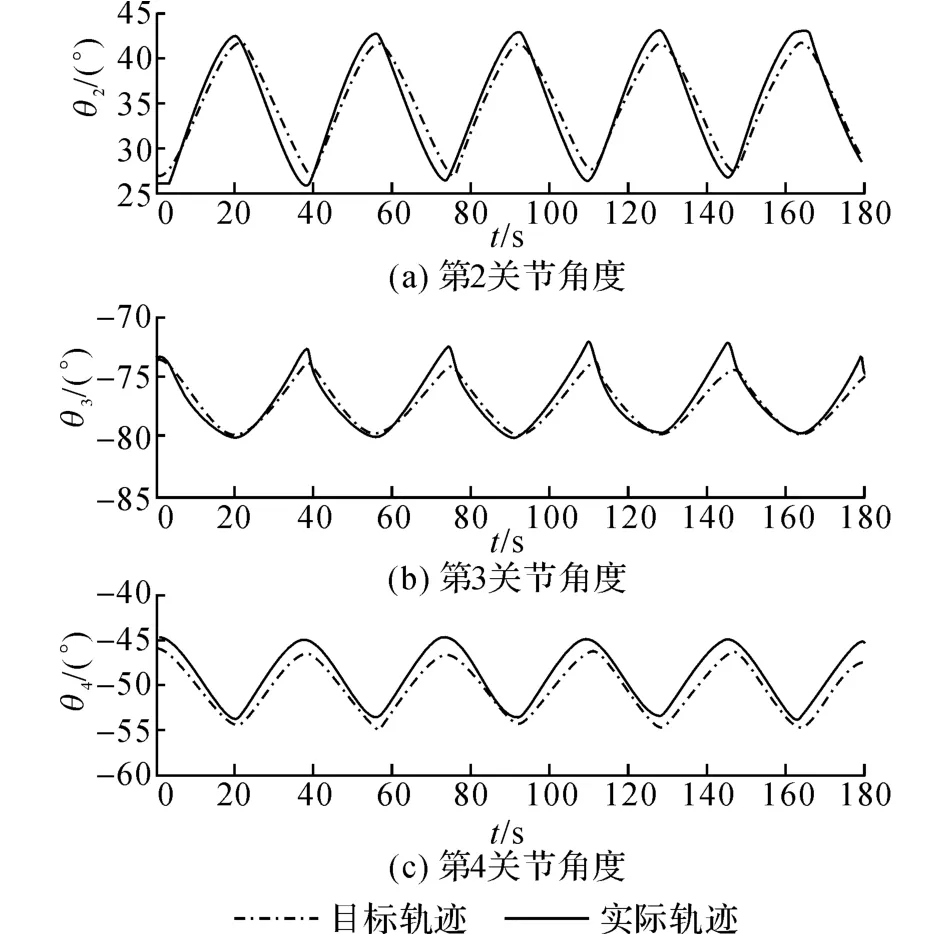
图3 竖直直线运动实验数据Fig.3 Experiment data during vertical linear motion
3.1 前馈补偿
为了消除控制上的误差,拟增加一个前馈补偿环节.前文已经提到,本文的设计基础是不加入传感器,采用开环控制,利用舵机内部电路进行闭环控制.在机器人运行的过程中,对于机器人的位置是未知的,只能通过对机器人动作完成情况的估计,得到各关节角度与理想角度之间的误差,从而利用前馈补偿的方法对误差加以消除.需要消除的误差主要有以下两类.
1)线性误差.线性误差产生的原因非常简单,主要是电路中各元器件自身的精度造成的,使得系统出现粗大误差,如初始位置不一致,理想轨迹与真实轨迹的斜率不一致等.线性误差不包括外界因素对舵机本身工作的影响.该误差的消除方法较简单,通过空载线性拟合得到,并非本文重点,后文不再进行分析.
2)非线性误差.产生非线性的因素有很多,如减速箱齿轮间隙导致回程差、摩擦等,尤其在大负载的情况下,摩擦的影响更突出.
利用前馈补偿的方式对上述误差进行消除,控制框图如图4所示.图中,θtgt为目标角度,elin、enln分别为当前状态下估计出的线性误差和非线性误差,θcmd为实际输入给舵机的指令角度,θout为实际输出角度.
系统包括2个前馈补偿环节,根据机器人当前位姿和目标位姿2个状态,估计运行过程中的elin和enln,对θtgt进行前馈补偿,得到θcmd,将其输入给舵机,即可输出误差较小的角度θout.
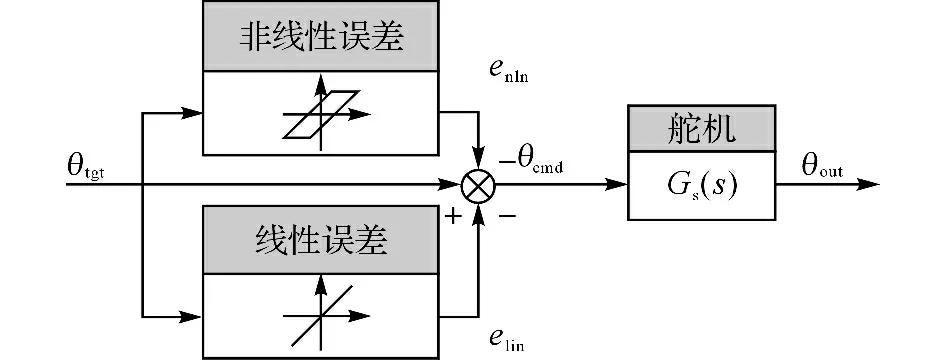
图4 前馈补偿控制方法Fig.4 Feedforward control method
3.2 非线性误差分析
分析产生非线性误差的原因有2个:1)机器人选用的是大功率舵机驱动,减速箱选用蜗轮蜗杆减速箱,在往复运动时可能会产生回程差以及较大的摩擦,导致某些非线性现象的出现.2)由于设计的需要,整个腿的重量很大,重量会导致机构的形变以及往复运动时可能导致运动性质不同,对信号的响应效果不一样.各关节受到的重力力矩不同,越靠近机身,重力矩越大,对舵机运动的影响越明显,其中以第二关节受重力影响最明显.下面关于非线性的分析均以第二关节为对象.
将5次实验结果进行滤波后,与理论轨迹进行对比,得到如图5所示的效果.图中,θr为实际运行轨迹.可以看出,这是一个非线性的环节,以图5的抬腿轨迹曲线为例,运动开始有一段回程差造成的饱和环节,后半部分是先滞后、后超前的摩擦环节,落腿轨迹也是同样的现象.本文参考LuGre摩擦模型[14],对该非线性环节进行描述.
为了方便分析,首先利用巴特沃兹方法对多组试验数据进行低通滤波,得到图6的点划线所示的滤波后试验数据.
为了描述方便,将该非线性环节分为2部分.其中,前后部分是斜率为0的饱和环节,中间用平行四边形描述摩擦造成的非线性环节,可得如下表达式:
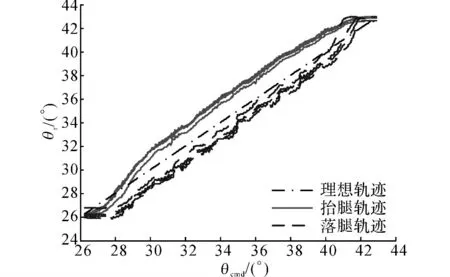
图5 单关节轨迹的非线性现象Fig.5 Nonlinear phenomenon of single joint trajectory

式中:(x0,y0)点为图中黑色直线的中点;a、b 分别代表红色轨迹饱和环节结束,进入摩擦环节的转折点距离中点x、y 方向上的偏移量;k1、k2分别为平行四边形两线段的斜率,k1为较短边;x1为平行四边形另一交点距离中点x 方向上的距离,可以通过其他已知量表达.
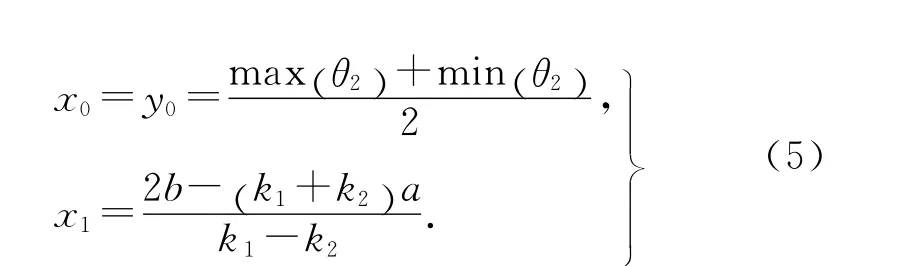
通过线性回归的方法,可得

图6 非线性现象的拟合结果Fig.6 Fit result of nonlinear phenomenon

将理论非线性线型与实际试验轨迹的滤波后结果进行对比,如图6 所示.线型回归的相关性系数R2=0.998 4,即线性回归的效果较好,可以利用该轨迹作为控制策略的设计依据.
4 试验验证
在加入前馈补偿后,再次控制机械腿完成同样的动作,并与前一次实验的数据进行对比,验证该前馈补偿环节对精度提高的效果.
4.1 竖直直线运动
在加入前馈补偿后,第二关节角度的曲线如图7所示.与图5对比可以看出,在中间段的误差得到了很好的消除,证明了该方法的可行性.在增加前馈补偿环节前,数据的平均误差为3.53%;其后,平均误差下降到1.02%,进一步证明了该方法的可行性.
分析数据可以发现,两端的误差较大,分析原因可能是在两端,非线性环节的正向是饱和阶段,为水平直线.在做逆解的过程中,该阶段的斜率无穷大;在实际控制中,该方程不存在,故给定大斜率进行逼近,这样可能造成两端刚进入饱和阶段时,系统出现偏离理论轨迹的现象,这是需要进一步改进的地方.
对第3和第4关节进行前馈补偿,以消除重力及回程差带来的非线性现象,足底轨迹误差得到了很好的消除,效果如图8所示.图中,z 为足底在机器人基坐标系中的足底的理想高度,e为足底实际位置与真实位置的误差距离.通过对比发现,加入补偿前后误差有了明显的减小,平均绝对误差为5.09 mm,满足了精度的要求.
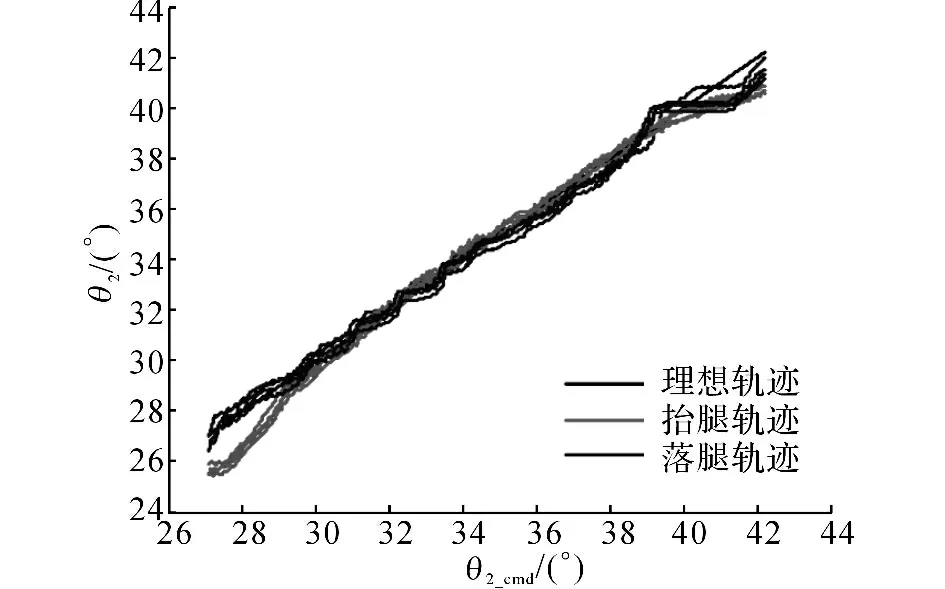
图7 加入前馈补偿后的结果Fig.7 Experiment result with feedforward compensation
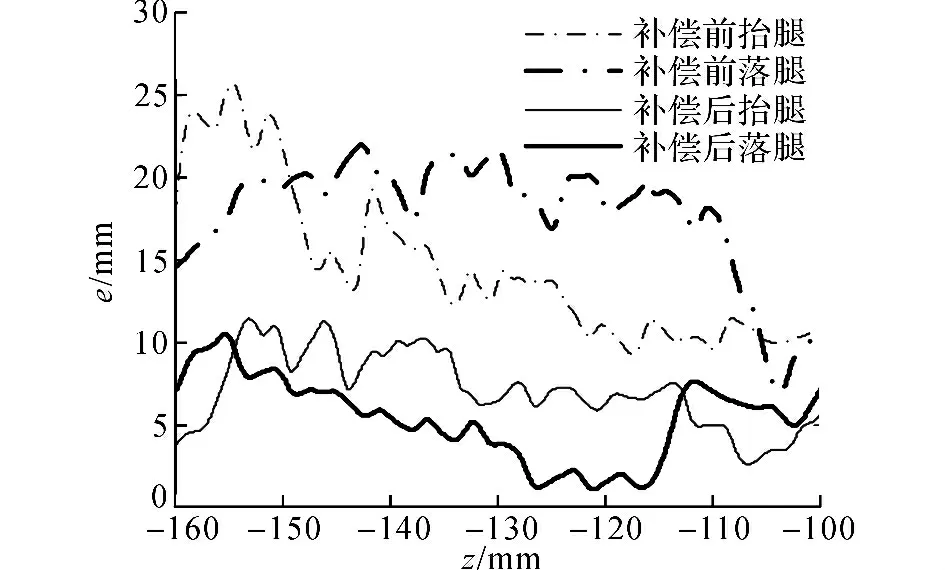
图8 竖直直线运动位置误差对比Fig.8 Comparison of position error during vertical linear motion
4.2 抛物线运动
为了更好地验证该策略的实用性,利用同样的控制策略,采用更广泛的足底抛物线的步态进行实验.抛物线轨迹如图9所示,轨迹为z=-0.028×(x-300)2-70,即初始高度为机器人机身坐标系的-140mm,向上抬起70mm;横向从250mm 处向外迈出100mm.

图9 抛物线运动机器人位姿Fig.9 Posture during parabola motion
由于抛物线结合了水平运动和竖直运动,且竖直方向上是往复运动,在加入前馈补偿前,机器人基本无法跟随理想轨迹,三关节的平均相对误差达到9.82%、3.50%、1.22%.在加入前馈补偿后,情况有明显改观,如图10所示.可以看出,多次试验的结果与理想轨迹基本重合,三关节的平均相对误差仅为1.06%、0.80%、0.96%.
对足底位置误差进行对比,如图11所示.在加入前馈补偿前,误差基本在30mm 以上,难以跟随;在加入前馈补偿后,误差基本可以稳定在10mm 内.
通过2种不同轨迹的验证可以发现,在加入前馈补偿后,单关节的跟随更加接近理想值,整个机器人表现的足底误差明显减小,充分证明了该控制策略的可行性.

图10 抛物线运动实验数据Fig.10 Experiment data during parabola motion
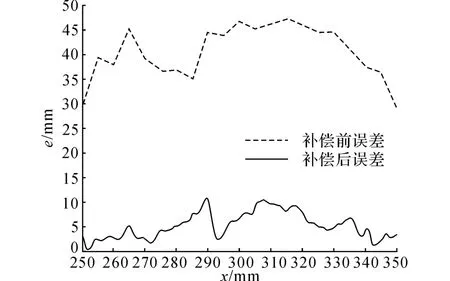
图11 抛物线运动位置误差对比Fig.11 Comparison of position error during parabola motion
5 结 语
本文建立机器人单腿运动模型,正确推导运动学正逆解,通过足底位置可以反算出各个关节的理论输入角度.通过完成运动学仿真,得到不同步态下,机器人足底运动轨迹以及各个关节理论输入角度的曲线.通过试验发现,由于回程差、重力等因素造成的滞环和饱和相结合的非线性环节,推导出理论表达式,并通过线性回归的方法得到参数.
在控制策略中加入了前馈补偿的环节,通过足底竖直直线和抛物线运动2种轨迹,验证加入该方法后角度相对误差稳定在1%左右.证明了该方法可以有效地减小轨迹跟随误差,使舵机可以较好地跟随理想曲线,从而验证了该方法的可行性.在负载较大或负载对舵机运行产生一定影响时,可以利用该方法有效地消除误差.
(
):
[1]NELSON G M,QUINN R D,BACHMANN R J.Design and simulation of a cockroach like hexapod robot[C]∥Proceedings of Robotics and Automation.Albuquerque:[s.n.],1997.
[2]KINGSLEY D A,QUINN R D,RITZMANN R E.A cockroach inspired robot with artificial muscles[C]∥Intelligent Robots and Systems.Beijing:[s.n.],2006:1837-1842.
[3]王倩,陈甫,臧希喆,等.新型六足机器人机构与控制系统设计[J].机械设计与制造,2008,3(3):148-150.WANG Qian,CHEN Fu,ZANG Xi-zhe,et al.Design of mechanism and control system of a new hexapod robot[J].Machinery Design and Manufacture,2008,3(3):148-150.
[4]林忠万,符强,李玉忍.基于DSP的导弹舵机控制系统的研究[J].航天控制,2004,22(1):46-49.LIN Zhong-wan,FU Qiang,LI Yu-ren.Study on missile actuation system based on DSP[J].Aerospace Control,2004,22(1):46-49.
[5]李赛辉,雷金奎.基于DSP 的数字舵机控制系统的设计与实现[J].计算机测量与控制,2009,17(3):484-486.LI Sai-hui,LEI Jin-kui.Design and implementation of digital rudder control system based on DSP[J].Computer Measurement and Control,2009,17(3):484-486.
[6]万彦辉,李存志,郭华,等.一种基于分形修正PID 算法的弹上舵机控制器[J].西安电子科技大学学报:自然科学版,2007,34(1):145-148.WAN Yan-hui,LI Cun-zhi,GUO Hua,et al.A steering gear system controller in missiles based on the fractal modified PID algorithm[J].Journal of Xidian University:Natural Science,2007,34(1):145-148.
[7]刘兴中,唐德宇,郑自伟,等.一种四轴舵机控制系统关键技术研究[J].微电机,2011,44(10):64-68.LIU Xing-zhong,TANG De-yu,ZHENG Zi-wei,et al.Research on several techniques of four axis rudder control system[J].Micromotors,2011,44(10):64-68.
[8]李全福,万彦辉,郭华.模糊PID 控制算法在电动舵机控制中的应用[J].微电机,2007,44(12):28-30.LI Quan-fu,WAN Yan-hui,GUO Hua.Study on fuzzy-PID control of electrical control actuator based on DSP[J].Micromotors,2007,44(12):28-30.
[9]董真,姜新建.舵机伺服系统优化控制策略的研究[J].微电机,2012,45(10):48-52.DONG Zhen,JIANG Xin-jian.Study on optimized control strategy of rudder servo system [J].Micromotors,2012,45(10):48-52.
[10]胡林.高精度舵机控制器的研制[D].西安:西安工业大学,2006.
[11]骆光照.电动舵机的鲁棒控制研究[D].西安:西安工业大学,2003.
[12]金波,陈诚,李伟.基于能耗优化的六足步行机器人力矩分配[J].浙江大学学报:工学版,2012,46(7):1168-1174.JIN Bo,CHEN Cheng,LI Wei.Optimization of energy-efficient torque distribution for hexapod walking robot[J].Journal of Zhejiang University:Engineering Science,2012,46(7):1168-1174.
[13]徐生林,刘艳娜.两足机器人的SimMechanics建模[J].浙大学报:工学版,2010(7):1361-1367.XU Sheng-lin,LIU Yan-na.Modeling of biped robot by SimMechanics[J].Journal of Zhejiang University:Engineering Science,2010(7):1361-1367.
[14]DE WIT C C,OLSSON H,ASTROM K J,et al.A new model for control of systems with friction [J].IEEE Transactions on Automatic Control,1995,40(3):419-425.
