Water Supply Networks as Cyber-physical Systems and Controllability Analysis
2015-08-09YongsongWeiandShaoyuanLi
Yongsong Wei and Shaoyuan Li
Water Supply Networks as Cyber-physical Systems and Controllability Analysis
Yongsong Wei and Shaoyuan Li
—Cyber-physical systems(CPS)is a system of systems which consists of many subsystems that can stand alone in an individual manner and can be taken as a typical complex network. CPS can be applied in the critical infrastructures such as water supply networks,energy supply systems,and so on.In this paper, we analyze the structure of modern city water supply networks from the view of CPS theory.we use complex network theory to build an undirected and unweighted complex network model for the water supply networks to investigate the structural properties, and present the structure of the water supply networks and detect communities by a spectral analysis of the Laplacian matrix.Then, we analyze the structure and controllability of water supply networks by the structural controllability method.The results show the feasibility and effectiveness of the proposed complex network model.
Index Terms—Cyber-physical system(CPS),water supply networks,spectral information,controllability
I.INTRODUCTION
Nowadays,certain infrastructures,such as water supply system,energy supply system,and transportation system,etc are consisted as the keystone and critical infrastructures of society development.The quality of the normal city life depends on these critical infrastructures.Critical infrastructures are increasing in complexity,because of the successful application of information and communication technologies.The current water supply system is a large and distributed network,and it is expanding rapidly to meet the increasing demands from industry and normal life in the bigger cities.These integrated systems are not only traditional embedded systems but also cyber-physical systems(CPSs).CPSs mainly take into account the interaction between the physical elements in the real world and the computing elements in the cyber space[1-4]. As described in[1],there are three key characteristics of CPSs.Firstly,the CPSs is a system of systems which consists of many subsystems that can stand alone in an individual manner.Secondly,there are novel interactions among control,communication,and computation.Last,the computing element in the cyber world should be tightly coupled with the physical systems in the real world.These three key characteristics bring a lot of challenges.Few of the challenges are robustness,safety and security[1,3].
The intrinsic nature of CPSs can be leveraged by exploiting the physical information on location and timing of the system[1].This paper focuses on the subsystems’interrelationship such as connectivity and controllability.The subsystems in the CPS can be taken as nodes in a complex network. The communications between subsystems can be taken as edges in a complex network.The CPS can be abstracted as a complex network system from the view of the data-accessing perspective of the subsystems.The paper[2]considers vehicular ad hoc networking(VANET)connectivity of platoon-based vehicular cyber-physical systems(VCPSs)where all vehicles drive in platoon-based patterns,which facilitate better traf fi c performance as well as information services.The number of the subsystems in the paper[2]is small and the connectivity condition is simple.In the complex network area,there are lots of results in connectivity and controllability.Capocci et al.[5]proposes a correlation in the spectral methods to detect community in complex network.Diao et al.[6]proposes an approach that could create boundaries for district metered areas automatically on the basis of the community structure of water distribution systems.Sheng et al.[7]improves the Capocci’s method by proposing addimensional eigenvector space.This paper uses complex network theory to analyze the complex network system modeling the water supply networks, and combine Capocci’s method and Sheng’s algorithm to detect communities in different states in a complex network system.
As it is well known,the CPSs grand challenges are in lots of areas such as biomedical and healthcare systems,nextgeneration air transportation systems and smart grid and renewable energy which are all critical areas.The controllability are the keys to these CPSs.For a classical CPS,it can be abstracted as a complex network system.As is known to all, it is hard to fi nd a suitable way to design controllers for a complex network system[8-9].In the year 2011,Liu et al.[10]developed analytical tools to study the controllability of an arbitrary complex directed network by identifying the set of driver nodes with time-dependent control that can guide the system’s entire dynamics.Liu also found that the number of driver nodes is determined mainly by the network’s degree distribution.Yuan et al.[11]proposes a framework of exact controllability as an alternative to the structural controllability framework,which offers a more general tool to treat the con-trollability of complex networks with arbitrary structures and link weights.In this paper we take a water supply network as an undirected and unweighted complex network and fi nd out driver nodes by Yuan’s method.
The remainder of this paper is organized as follows.Section II analyzes a cyber-physical system structure for the water supply networks and proposes a complex network model. Section III introduces a spectral analysis method to detect the communities in the complex network,then use this method to detect the water supply networks.Section IV discusses the structural controllability of the water supply networks and design controllers for a complex network system.Section V discusses the limitation and improvement of this research.
II.PROBLEM STATEMENT
The area of the Shanghai water supply is more than 190 square kilometres.The length of the pipe network is 2848 kilometres,and the pipe diameter is between 500mm and 2000mm.Main pipes are directly connected to the water distribution system.The water of the Shanghai city is supplied by four water supply companies which are South City Water Supply Company,North City Water Supply Company,Pudong Veolia Water Supply Company and Minhang Water Supply Company.These four companies contain 14 water plants and 51 boostering pumps which can supply 6 million tons water per-day for the whole city.The real water supply network is very complicated as in Fig.1,which is the Shanghai water supply system made up with pipes having diameter over 800mm.In Fig.1,dots represent the main pumps and water plants in the water supply system.
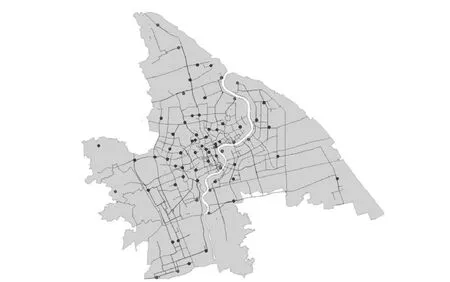
Fig.1.The geographic information system of Shanghai water supply networks.
The city water supply networks contain water plants,pump stations,reservoirs and pipes shown in Fig.2.In the water plant,the raw water undergoes a process of pretreatment, dosing,precipitation, fi ltration and advanced treatment,then the pure water is stored in the reservoir of the water plants. The high power pump stations transport the pure water to the water supply network.In the network,there are lots of pump stations which can guarantee the pipe pressure at a suitable level which can supply water to every customer,considering the loss of water head.
Supervisory control and data acquisition(SCADA)systems are widely used in the modern water supply system.Fig.3 shows the interactions between distributed areas and SCADA systems.Based on the information from the SCADA systems, we can get the node model and the predictive instantaneous demand,then the optimal setpoints can be sent to the distributed areas via SCADA systems.
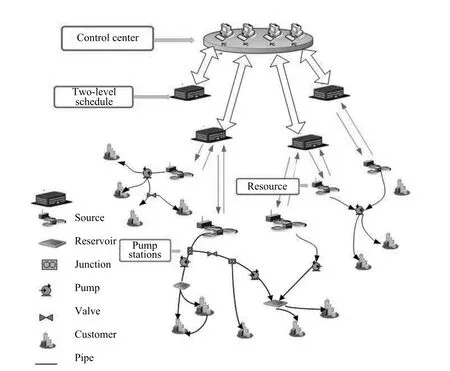
Fig.2.Distributed network of water supply networks.

Fig.3.SCADA information structure of water supply networks.
A water supply system is a critical infrastructure which can be modeled as a complex network of pipelines CPS.The distribution center contains an embedded computer that coordinates directly with physical components such as actuators via actuating signals to maintain control over the pipeline shown in Fig.4.An embedded computer comprises long-term control and automation control subsystems.The long-term control is used to communicate with neighboring distribution areas and coordinate the distributed setpoints of water.There areNdistributed areas in the water supply network.

Fig.4.Interactions with in pipelines network with cooperating distributed areas.
In the complex network theory,we use lots of symbols from the graph theory to describe a complex network.LetG=(V,E)be an undirected graph withnnodes andmundirected edges.
N={1,2,...,n}denotes the sets of all vertices andL={l1,l2,...,lm}denotes the sets of all edges.For an edgelconnecting nodeiand nodej,we de fi ne a column vectoral∈Rn,whereali=1,alj=1,and other elements are zeros. We can get an adjacency matrixAwhich is used to illustrate the connection of a graph.Generally,there are lots of nodes or subsystems in the CPS,we take those nodes or subsystems as nodes in a complex network.
According to these de fi nitions,we can get a complex network system from a water supply system which is a part of water supply networks in the Shanghai city shown in Fig.5. There are 198 nodes and 298 edges in Fig.2.The nodes which have the same color has the same degree.Actually,in the real water supply system,most links are bilateral except a small number of inlet branches.In order to simplify the network,all bilateral links are taken as unilateral shown in Fig.5,which is the ForceAtlas2 layout graph[12].Each node has a unique ID number.
In order to get more topological information,we need the Laplacian matrix of the complex network.Laplacian matrixLis de fi ned as follows:

whereAis the adjacency matrix of the topology which can be written as

Dis the diagonal matrix which can be written as

Fig.5.The complex network of pipeline CPSs.

diis the degree of the nodeiwhich means the connection from nodeito other nodes.
The spectrum of Laplacian matrix contains much topological information of the complex network.We de fi ne the eigenvalues of the Laplacian matrix asλ(L)=λ1,λ2,...,λn. Without loss the generality,we assumeλ1≤λ2≤λ3≤···≤λn.Then we can get some properties of the Laplacian matrix[7].
1)Lhas only real eigenvalues;
2)λ1=0 andλ2≥0 if and only if the graph is full connected;
3)λ1=0 and its corresponding eigenvector is constant (all components of this vector are the same).The multiplicity of zero eigenvalues is determined by the number of splitting components of the graph.
In the complex network like Fig.2,we can getλ1=0 andλ2=0.0127,other eigenvalues are real.According to the properties of the Laplacian matrix,the graph is full connected, and has no isolation part.
III.SPECTRAL ANALYSIS OF THE PIPELINESCPSOF WATER SUPPLY NETWORKS
A.Spectral Analysis Theory
The traditional spectral bisection method is based on that components in the eigenvectors corresponding nonvanishing eigenvalues have approximately equal value corresponding nodes in the same community.It is very useful to have a clear partition in the network.As long as the partition is suf fi ciently sharp,the components in the eigenvectors are step-like.
However,in the real large complex network systems,there is no clear partitioning and the precise value of the eigenvectorcomponents is of little use.In the pipelines CPS,the typical eigenvector pro fi le is not step-like[5].However,such characteristic patterns are much clear ind(d≥2)dimensional eigenvector space,which is consisted ofdeigenvectors of the fi rstdnonvanishing eigenvalues[7].Then we can get the community detection algorithm as follows:
Step 1.Use the data of the pipelines CPS network,and transfer the real network to the complex network.
Step 2.Get the adjacency matrixAand the Laplacian matrixL.
Step 3.Get the eigenvalues of the Laplacian matrixL:λ(L) =λ1,λ2,...,λn.
Step 4.If the multiplicity of vanishing eigenvalues of the Laplacian matrixLis 1,then there is no isolated community in the network.Get the fi rst 2 dimensional eigenvector space,and identify the communities in the network.Then the algorithm is done.If the multiplicity of vanishing eigenvalues is not 1, then there is isolated community.Identify communities,and fi nd potential communities.Go to the Step 2.
Remark 1.If the graph of the network is not full connected or there are some isolate nodes,the multiplicity of vanishing eigenvalues of the matrixLis bigger than 1 via the properties of the Laplacian matrix,we should choose the eigenvector space of the fi rst 2 nonvanishing eigenvalues.All isolate nodes are at the(0,0)in the eigenvector space.
B.The Application of Spectral Analysis Theory:the Pipelines CPS of Water Supply Networks
We take the pipelines CPS of part of water supply networks in the Shanghai city as an example.We assume two states of the pipelines CPS:the original state,and state 2(edgel177,145and edgel127,112burst in an unexpected event.That means communications between distribution area 177 and distribution area 145,distribution area 127 and distribution area 112 have got broken).The proposed algorithm is applied to detect isolated communities.
We use the software“Gephi”and“Pajek”to get the adjacency matrixAand the Laplacian matrixL,which have 198×198 dimension.Then,we use Matlab to get the eigenvalues and the eigenvectors of the Laplacian matrixL.According to the algorithm,λ1=0 andλ2=0.0127,and the multiplicity of vanishing eigenvalues of the Laplacian matrixLis 1.Then, we get the 2 dimensional eigenvector space made up with two eigenvectors according to the fi rst 2 nonvanishing eigenvalues shown in Fig.6.
In the original state of the pipelines shown in Fig.6,we can get three areas roughly according to the spectral distribution shown in Table I.There are 80 nodes in Area1,67 nodes in Area2,and 51 nodes in Area3.All the three areas are connected.
In the state 2,l177,145andl127,112burst in an unexpected event[13].By the same method,we can get the spectral information shown in Fig.6.From the eigenvalues of the Laplacian matrixL,we can see the multiplicity of vanishing eigenvalues of the Laplacian matrixLis 2 so that there is an isolated community,which are the spot(0,0)in Fig.7.There are 80 nodes in the new isolated community.The details about the new Area1 are shown in Table II.

Fig.6.Original state of the pipelines.
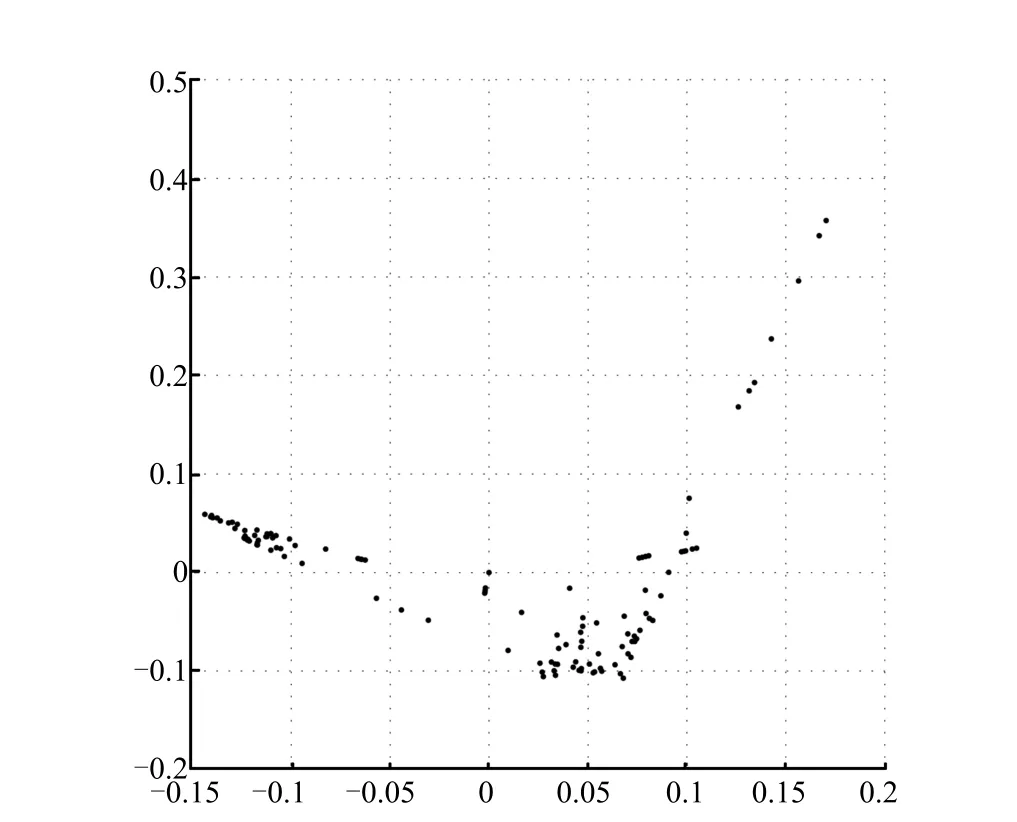
Fig.7.State 2 of the pipelines.
The spectral analysis can provide a deep analysis of the pipelines including the structural connectivity and the vulnerability,and it is also useful to devise countermeasures when unexpected events happen.The spectral analysis can also be suitable for other CPSs.
IV.STRUCTURAL CONTROLLABILITY OF THE PIPELINE CPSOF WATER SUPPLY NETWORKS
A.Structural Controllability of Complex Networks
Consider a network ofNnodes described by the following set of ordinary differential equations:

where the vectorxxstands for the states of nodes,A∈RN×Nstands for adjacent matrix of the network,in whichaijrepresents the weight of a directed link from the nodeitoj(for undirected unweighted network,aij=aji=1).uuis the controller.Bis control matrix.The standard way to address the controllability problem is to fi nd a suitable control matrixBof a minimum number of driver nodes so as to satisfy the stability condition[10-11].

TABLE I SPECTRAL INFORMATION OF ORIGINAL STATE

TABLE II SPECTRAL INFORMATION OF STATE 2
Yuan et al.[11]developed a general theory to calculate the minimum numberNDof independent drivers or controllers based on the Popov-Belevitch-Hautus(PBH)rank condition (ND=min{rank(B)}).For arbitrary matrixA,the minimum numberNDis determined by the maximum geometric multiplicityµ(λi)of the eigenvalueλiofA.From the idea in the paper[11],we can get the algorithm as follows:
Step 1.Get the adjacency matrixAand eigenvalues of the adjacency matrix.
Step 2.Get theA-λi×IN,λiis the eigenvalue which has the algebraic multiplicity bigger than one.Convert theA-λi×INto the column canonical form by Gaussian elimination method.Find the maximum geometric multiplicityµ(λM).
Step 3.Find the minimum driver node or controllers by linearly dependent rows in theA-λM×IN.
Remark 2.By the algorithm,we can get the minimum number of the driver nodes for a complex network and the driver nodes set which contains all possible driver nodes. Without loss of generality,we get the driver nodes group as one of the groups in the driver nodes set in the sequel.
罗爹爹说:“有钱了也要对我们穷人好呀。不能光是屁颠屁颠地跟在有钱人后面跑,是不是?不说别的,那个 样子都蛮掉底子。”
B.Structural Controllability of the Pipelines CPS of Water Supply Networks
To count the algebraic multiplicity,we set a small threshold 10-8.If the absolute difference between two eigenvalues is less than threshold,the two are regarded as identical.We use the original state of part of Shanghai pipelines system as the control plant.We can get eigenvalues of the adjacency matrixA.
There are two eigenvalues 1 and-1 which have the algebraic multiplicity bigger than 1.The algebraic multiplicity of the eigenvalue 1 is two,and the other is four.By the algorithm mentioned,the geometric multiplicity of the eigenvalue 1 is two,the geometric multiplicity of the eigenvalue-1 is four shown in Fig.8(the arrow points out four nodes).So we can get that


Fig.8.Original eigenvalues of the pipelines.
The maximum geometric multiplicityµ(λM)is four.So we can get the column canonical form of matrixA-λM×INand fi nd linear dependent rows:149,185,194,195.The number 149 is the node 149 in the pipelines system,others are,251, 215,196 as shown in Fig.9.
In the original state,the node 40,149 and 251 are in Area3, the node 215 is in Area2,and the node 196 is in Area1.These four nodes are minimum drivers nodes.The minimum driver nodes set is the same as in the original state when we use the algorithm to analyze the state 2 in which there is an isolatedcommunity while the edgel177,145and the edgel127,112are out of order.

Fig.9.Driver nodes in the complex network of the pipelines.
In the state 2,there are 80 nodes in the isolated community as shown in Table II.we use the algorithm to analyze the 80 nodes,and get the driver nodes 196,215 which are the same as two driver nodes in the original state with 198 nodes(the number of the driver nodes is the same and the driver nodes are not the same,we pick the same driver nodes from the driver nodes set).
In order to testify whether we can control all of the 80 nodes with the driver node 196 and 215,we choose the system which has the discrete state spaceA80×80just as the same as the structural matrix formed by the topology in Table II.
The control matrixB80×2is constructed by the method mentioned in the supplementary material of the Yuan et al.[11]. Using the nonsingular transformation
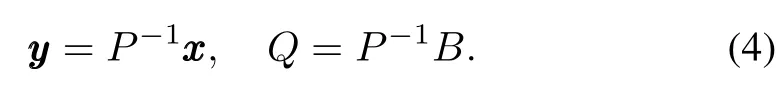
The system can be rewritten in the following Jordan form:

Based on the method mentioned in the supplementary material of the Yuan et al.[11],we can get the simplestQand constructQby assigning value one to the row ofQcorresponding to the last row of every Jordan sub-block ofJ(λi).Then,we can get the complete structure information ofBby the following

For a node in a CPS network of water supply system,the node dynamic process system can be described as follows:
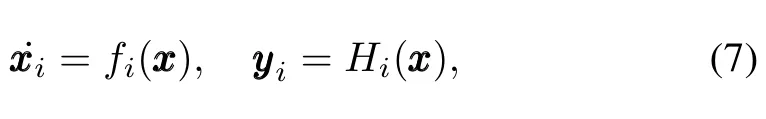
wherexxiis the node state,yyiis the node output,andfi(xx) is a linear or nonlinear function.According to the network,a node’s output may be the neighbor nodes’input.The dynamic process system for a node in the CPS network can be written:

wherec>0 is the coupling strength between nodes,lijis the element of the Laplacian matrixLmentioned above.
C.Simulations for the Application of Structural Controllability
Without loss of generality,we choosefi(xx)=xxi,c=1,H(xxi)=1 to show the structural controllability of the CPS network here.Then,we can design controllers to control all 80 nodes according to the system parametersAandB.As we know,there are two driver nodes in the 80 nodes,we just need to design a controller to control two nodes.The number of the controllers are causal,one can choose a single controller or any number of controllers.In order to show the result is feasible,we design two PID controllers for the system shown in the Fig.10.There are two closed loops in order to control two nodes’state respectively.

Fig.10.The control block diagram with two driver nodes.
Based on the state matrixA,each node is an integrator. The connectivity relationship between nodes are also described in the state matrixA.The driver nodes 196 and 215 are nodes 36 and 37 in Fig.10 which are controlled by two PID controllers.We regulate some PID parameters to get appropriate performance as shown in Fig.11.Fig.12 shows that non-driver nodes can be stable while the two diver nodes are stable.
Remark 3.According to the algorithm,we can get the minimum number of driver nodes in the pipelines CPS of water supply networks and speci fi c driver nodes set.Choosing appropriate control inputs can guarantee the structural controllability of the CPS network.If the systemAis in canonical Jordan form,we can see the difference between the driver nodes and normal nodes obviously.The result of the driver nodes is useful for engineers to design the controllers and choose the control inputs in the pipelines CPS of water supply networks or other CPSs networks.
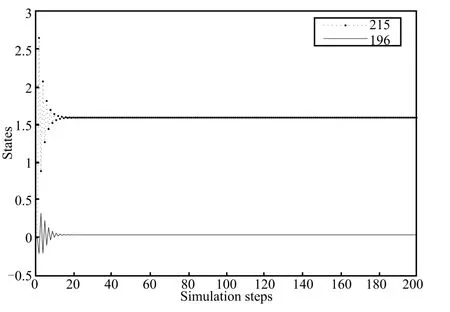
Fig.11.Simulation results of driver nodes with two PID controllers.

Fig.12.Simulation results with two PID controllers.
V.CONCLUSION
In this paper,we use the complex network and graph theory to analyze the structural properties of the pipelines CPS of water supply networks.We build a complex network model for the pipelines CPS of water supply networks,and use some metrics mentioned above to investigate the structural properties of the pipelines CPS,which can be used to guide the construction of the of water supply networks and improve the robustness of water supply networks.The algorithms mentioned in the paper are also useful for complex networks of other CPSs.
REFERENCES
[1]Park K J,Zheng R,Liu X.Cyber-physical systems:milestones and research challenges.Computer Communications,2012,36(1):1-7
[2]Jia D Y,Lu K J,Wang J P.On the network connectivity of platoonbased vehicular cyber-physical systems.Transportation Research Part C: Emerging Technologies,2014,40:215-230
[3]Akella R,Tang H,McMillin B M.Analysis of information fl ow security in cyber physical systems.International Journal of Critical Infrastructure Protection,2010,3(3-4):157-173
[4]Park S,Kim J H,Fox G.Effective real-time scheduling algorithm for cyber physical systems society.Future Generation Computer Systems, 2014,32:253-259
[5]Capocci A,Servedio V D P,Caldarelli G,Colaiori F.Detecting communities in large networks.Physica A:Statistical Mechanics and Its Applications,2005,352(2-4):669-676
[6]Diao K G,Zhou Y W,Rauch W.Automated creation of district metered area boundaries in water distribution systems.Journal of Water Resources Planning and Management,2012,139(2):184-190
[7]Sheng N,Jia Y W,Xu Z,Ho S L,Kan C W.A complex network based model for detecting isolated communities in water distribution networks.Chaos:An Interdisciplinary Journal of Nonlinear Science,2013,23(4): 043012
[8]Lombardi A,H¨ornquist M.Controllability analysis of networks.Physical Review E,2007,75(5):056110
[9]Nepusz T,Vicsek T.Controlling edge dynamics in complex networks.Nature Physics,2012,8(7):568-573
[10]Liu Y Y,Slotine J J,Barab´asi A L.Controllability of complex networks.Nature,2011,473(7346):167-173
[11]Yuan Z Z,Zhao C,Di Z R,Wang W X,Lai Y C.Exact controllability of complex networks.Nature Communications,2013,4:Article number: 2447,doi:10.1038/ncomms3447
[12]Jacomy M,Heymann S,Venturini T,Bastian M.Forceatlas2,a continuous graph layout algorithm for handy network visualization.Medialab Center of Research,2011,560-1-22
[13]Wang S L,Hong L,Ouyang M,Zhang J H,Chen X G.Vulnerability analysis of interdependent infrastructure systems under edge attack strategies.Safety Science,2013,51(1):328-337

Wei
the B.Sc.and M.Sc.degrees from Shanghai Jiao Tong University,China in 2008 and 2013,respectively.Now he is a Ph.D. candidate in the Department of Automation,Shanghai Jiao Tong University,China.His research interests include distributed model predictive control and large-scale systems.

Manuscript received November 3,2014;accepted February 9,2015.This work was supported by National Natural Science Foundation of China(612 33004,61221003,61374109,61104091,61304078,61473184),National Basic Research Program of China(973 Program)(2013CB035500),the International Cooperation Program of Shanghai Science and Technology Commission(12230709600),the Higher Education Research Fund for the Doctoral Program of China(20120073130006,20110073110018),and the China Postdoctoral Science Foundation(2013M540364).Recommended by Associate Editor Xinping Guan.
:Yongsong Wei,Shaoyuan Li.Water supply networks as cyberphysical systems and controllability analysis.IEEE/CAA Journal of Automatica Sinica,2015,2(3):313-319
Yongsong Wei and Shaoyuan Li are with the Department of Automation, Shanghai Jiao Tong University,and Key Laboratory of System Control and Information Processing,Ministry of Education of China,Shanghai 200240, China(e-mail:yswei@sjtu.eud.cn;syli@sjtu.edu.cn).
Shaoyuan Li received the B.Sc.and M.Sc.degrees in the Department of Automatic Control, Hebei University of Technology in 1987 and 1992, respectively,and the Ph.D.degree from Nankai University in 1997,all in China.He is currently a Distinguished Professor with the Department of Automation,Shanghai Jiao Tong University,China. His research interests include distributed predictive control,networked control systems,dynamic system optimization,and performance assessment.Corresponding author of this paper.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- End-to-end Delay Analysis for Mixed-criticality WirelessHART Networks
- An Algebraic Detection Approach for Control Systems under Multiple Stochastic Cyber-attacks
- A Stochastic Programming Strategy in Microgrid Cyber Physical Energy System for Energy Optimal Operation
- Distributed Secondary Control and Optimal Power Sharing in Microgrids
- Cost Minimization of Wireless Sensor Networks with Unlimited-lifetime Energy for Monitoring Oil Pipelines
- Guest Editorial for Special Issue on Cyber-Physical Systems
