Distributed Secondary Control and Optimal Power Sharing in Microgrids
2015-08-09GangChenandEningFeng
Gang Chen and Ening Feng
Distributed Secondary Control and Optimal Power Sharing in Microgrids
Gang Chen and Ening Feng
—We address the control problem of microgrids and present a fully distributed control system which consists of primary controller,secondary controller,and optimal active power sharing controller.Different from the existing control structure in microgrids,all these controllers are implemented as local controllers at each distributed generator.Thus,the requirement for a central controller is obviated.The performance analysis of the proposed control systems is provided,and the fi nite-time convergence properties for distributed secondary frequency and voltage controllers are achieved.Moreover,the distributed control system possesses the optimal active power sharing property.In the end,a microgrid test system is investigated to validate the effectiveness of the proposed control strategies.
Index Terms—Microgrid,droop control,distributed control, optimal control.
I.INTRODUCTION
CONCERNS about increased energy demand,energy reliability,and environmental pollution have increased interest in the application of renewable energy.The traditional electrical power grid will undergo some structural change with the penetration of renewable energies.The renewable energies are often widely distributed.A promising solution to interfacing the distributed energy with grid is the microgrid paradigm[1-2]. A microgrid may comprise a cluster of loads and a variety of inverter-interfaced distributed generation systems such as photovoltaic arrays,wind turbines,fuel cells,and geothermal energy.Microgrid can be operated either in grid connected or islanded(autonomous)modes[2].
The distributed renewable resources generate either variable frequency AC power or DC power,and are interfaced with a synchronous AC grid via power electronic AC/DC/AC or DC/AC inverters.In islanded operation,inverters generally operate as voltage source inverters.Each distributed generator (DG)is connected to the microgrid through a voltage source inverter.The main challenge for autonomous microgrid is the coordination of the generators for the active and reactive power sharing and the control of system voltage and frequency.The early work[2-5]introduced the concept of conventional frequency and voltage droop control to microgrid in inductive networks.The droop control is a proportional control law and enables good sharing for loads[2-3].To enhance redundancy and enable plug-and-play functionality of microgrids,the decentralized droop control has been extensively studied[4-8].Once a microgrid is islanded from themain power grid,the primary droop control cannot avoid voltage and frequency deviations from nominal values.A way to restore the microgrid voltage and frequency is to employ the secondary integral control schemes[9-12].The conventional secondary control system is centralized such that complicated communication networks are required to collect information globally and a powerful central controller is used to process the huge amount of data[10,13].To minimize the communication complexity and allow the plug-and-play operation of microgrids,the distributed secondary control schemes are proposed and investigated in recent years.The work in [12]presented a distributed averaging-proportional-integral controller to regulate the system frequency by applying the ideas from multi-agent systems[14-18].The work in[9,14] formulated the secondary control problem of microgrids as a tracking synchronization problem of multi-agent systems where the voltages and frequencies of distributed generators are required to track their nominal values.The above work only considered the case that the inverters share the total load proportionally according to their power ratings.To guarantee the lowest operating cost while maintaining system generationdemand balance constraints,we need to fi nd an optimal power output combination of all generators.That is,a highlevel tertiary controller should be designed to facilitate an economical operation.The tertiary controllers in the traditional power systems are implemented in a centralized computing unit.Considering the fl exibility structure and plug-and-play property of microgrids,decentralized optimal control is more preferable.
Although signi fi cant progress has been made for the microgrid control system design,several important issues left to be further considered include the following:1)designing a fully distributed control system that allows a plug-and-play operation;2)achieving the distributed and optimal power sharing control among the distributed generators;3)guaranteeing the prescribed control performance for the distributed secondary control and the optimal power sharing properties.
Comparison with existing work in the literature:Motivated by the hierarchical structure of power systems,we consider a totally distributed implementation of the primary,secondary, and tertiary control levels.The hierarchical structure proposed in[10,13]needs a central controller.In contrast,the central controller is not required in our work.The distributed secondary strategies presented in[9,12]only guarantee the asymptotical voltage and frequency restoration control.Our strategy achieves the fi nite-time voltage and frequency restoration control.Compared with the works in[9,12,14]where only the proportional power sharing property is guaranteed, our method achieves the optimal power sharing.The major contributions of this paper can be summarized as follows.
1)We present a new control system for autonomous microgrid,where the primary control,secondary control,and tertiary control are locally implemented at each DG.In contrast to the existing literatures[1-14],the proposed control schemes arefully distributed.
2)A distributed architecture for optimal dispatch of generations in microgrids is proposed.Each generator only communicates with its neighbors to achieve a minimal generation cost while satisfying the demand constraint.
3)A class of distributed secondary controllers,which possess the fi nite-time convergence property,are presented in this paper.The convergence performances of the secondary control are improved.
The rest of the paper is organized as follows.Section II gives the microgrid structure.Distributed secondary voltage and frequency control is presented in Section III.Distributed and optimal active power sharing scheme is developed in Section IV.To demonstrate the effectiveness of the proposed algorithms,numerical examples are presented in Section V. Finally,we conclude the paper in Section VI.
II.MICROGRID STRUCTURE
Since the centralized control structure in microgrids requires a central controller,this structure decreases the systems reliability and scalability.A solution to this problem is to employ the distributed control structure which has the capability of enhancing redundancy and enabling plug-and-play function in microgrids.Inspired by the hierarchical control scheme of microgrids,we present a fully distributed control structure as shown in Fig.1.The microgrid system,which is a typical cyber-physical system,comprises the physical electric power network(see Fig.1(a))and the cyber communication network(see Fig.1(b)).The control structure(see Fig.1(c)) consists of the primary controller,the secondary voltage and frequency controller,and the active power sharing controller. Different from the traditional hierarchical control scheme of microgrids,the primary,secondary,and tertiary controllers are implemented as the local controllers at each DG.We fi rst analyze the primary controller.The other control modules will be discussed in the subsequent sections.
Droop control is widely used in the control of large-scale power networks.This technique has been adapted to inverterbased microgrids[2-5].The power controller,shown in Fig.2, is based on microgrid frequency and voltage droop method. Droop technique gives a relation between the active power and the frequency and a relation between the reactive power and the voltage magnitude.Let the output voltage be expressed in the direct-quadratic(d-q)reference frame.The output voltage magnitude reference is aligned to the d-axis.The q-axis reference is set to zero.As in[2,9],the frequency and voltage droop characteristics can be expressed as:
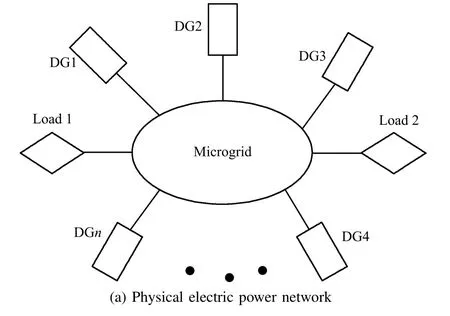

Fig.1.A fully distributed microgrid control system.
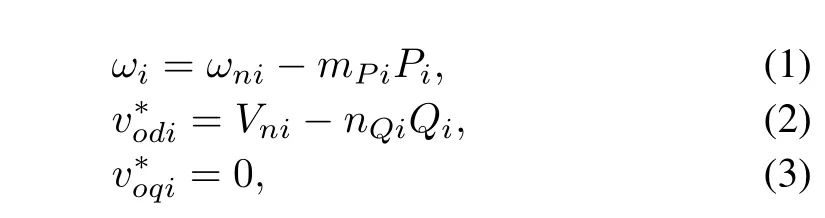
whereωiandare the reference frequency and magnitude of DG output voltage,respectively.mPiandnQiare the droop coef fi cients.ωniandVniare the primary control references.PiandQiare the measured active and reactive powers at the DGs terminal,which are generated by a low pass fi lter with cutoff frequency equal toωci.The differential equation of the power controller can be written as
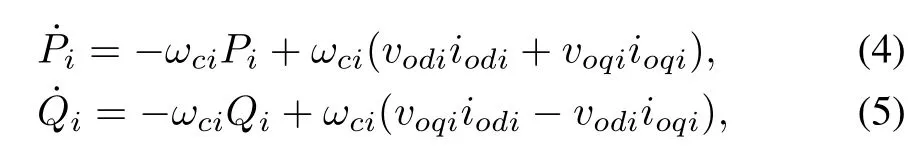
wherevodi,voqi,iodi,andioqiare the direct and quadratic components of output voltage and output current,respectively.
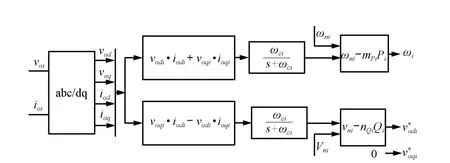
Fig.2.Power controller.
Remark 1.The cyber communication network can be different from the physical electric power network.A sparse communication network can be designed such that the complexity of the whole systems is reduced.The sparse commu-nication network is accommodated by utilizing the following distributed secondary and tertiary control strategies.
III.DISTRIBUTED SECONDARY VOLTAGE AND FREQUENCY CONTROL
A.Distributed Secondary Voltage Control
Since the dynamics of the voltage and current controllers are much faster than the dynamics of the power controller[5,9], the voltage droop characteristics can be written as
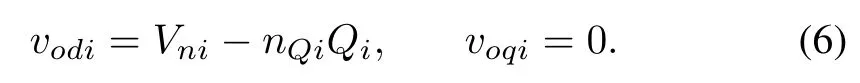
The amplitude of the DG output voltage is

Thus,the synchronization of the voltage amplitude can be achieved by choosing the control inputVni,such thatvodi→vref,wherevrefis the output voltage magnitude reference.
Differentiating the voltage-droop characteristic in(6)yields
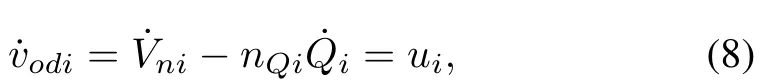
whereuiis an auxiliary controller to be designed.The secondary voltage control inputVnican be calculated based on the auxiliary control inputui.Since the microgrid structure is distributed and there is no central controller,only a subset of DGs has access to the voltage magnitude reference.To achieve the synchronization forvodi,the distributed cooperative control schemes are applied such that the auxiliary controller is constructed by only using the own information of each DG and the information of its neighbors.The distributed algorithm can realize the plug-and-play capability of microgrid.A graph is used to describe the communication topology in microgrids. DGs are considered as the nodes of the communication graph. The edges of the graph denote the communication links.A graph is usually expressed asG=(ν,ε,A)with a non-empty fi nite set ofnnodes,a set of edgesε⊂ν×ν,and the associated adjacency matrixA=[aij]∈Rn×n,whereaii=0 andaij≥0 for all.aij>0 if and only if there is an edge between vertexjand vertexi.Ni={j∈ν:(j,i)∈ε}denotes the set of the neighbors of nodei.A diagonal matrixD=diag{di}withdi=Pj∈Niaijis called a degree matrix ofG.The matrixL=D-Ais called the Laplacian matrix. A path is a sequence of edges of the form(i1,i2),(i2,i3),...,whereij∈ν.A graph is called connected if there exists a path between any distinct pair of nodes.
Let the node with index 0 denote the virtual leader which provides the voltage reference value.According to(8),we have

Letsig(x)α=sign(x)|x|α,wherex∈R,α>0, and sign(·)denotes the signum function.For any vectorsp=(p1,p2,...,pn)Tandq=(q1,q2,...,qn)T,denotep⊙q=(p1q1,p2q2,...,pnqn)T.For a vectorx=(x1,...,xn)T,sig(x)α=sign(x)⊙|x|αwith sign(x)= (sign(x1),sign(x2),...,sign(xn))Tand|x|α=(|x1|α,|x2|α,...,|xn|α)T.Note thatsig(x)αis a continuous function with respect toxwhenαis bigger than 0.
To guarantee the fi nite-time synchronization of the voltage control systems,the following distributed controller is proposed
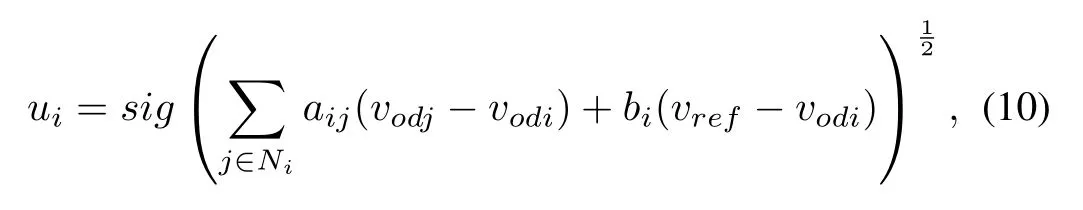
wherebi≥0 is the weight of the edge by which thei-th DG has access to the voltage reference.Let

Furthermore,we have
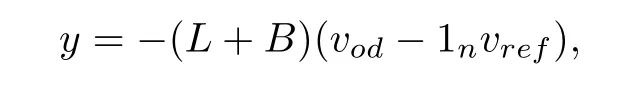
wherey=(y1,y2,...,yn)T,vod=(vod1,vod2,...,vodn)T,B=diag{bi}is a diagonal matrix with thei-th entry beingbi,and 1ndenotes then-th vector with all the entries being 1.
The following lemmas are required in the subsequent analysis.
Lemma 1[15].If the graphGis undirected and connected, thenL+Bis positive de fi nite.
Lemma 2[18].Let the graphGbe connected andB/=0. Then
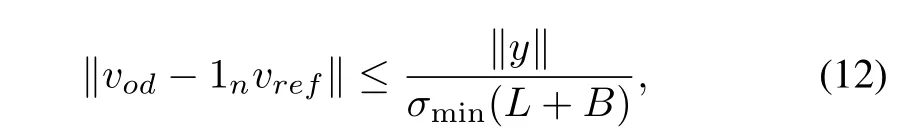
withσmin(L+B)as the minimum singular value ofL+B, andy=0 if and only if the output voltages of each DG synchronize,that is,vod=1nvref.
Lemma 3[19].Letr1,r2,...,rn≥0 and let 0<ρ≤1, then
Lemma 4[20].Consider the continuous function˙x=f(x) withf(0)=0.Suppose that there isC1functionV(x)de fi ned on a neighborhood of the origin,and there are real numbersc>0 and 0<α<1 such thatV(x)>0 and˙V(x)+cVα(x)≤0.Then the origin of the system is locally fi nitetime stable.Moreover,the settling time,depending on the initial statex(0)=x0,satis fi esT(x0)
Now we give one of the main results.
Theorem 1.Consider the secondary voltage control system (8).Let the communication topology be connected andbi/=0 for at least one DG.Under the auxiliary control inputuigiven in(10),the output voltage direct termvodiof each DG synchronizes with the reference valuevrefin fi nite time.
Proof.Choose the Lyapunov function
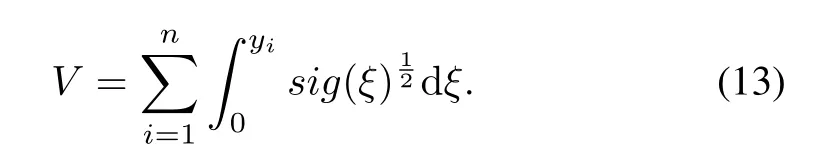
It is obvious thatV≥0 andV=0 if and only ify=(y1,y2,...,yn)T=0.The time derivative ofVis
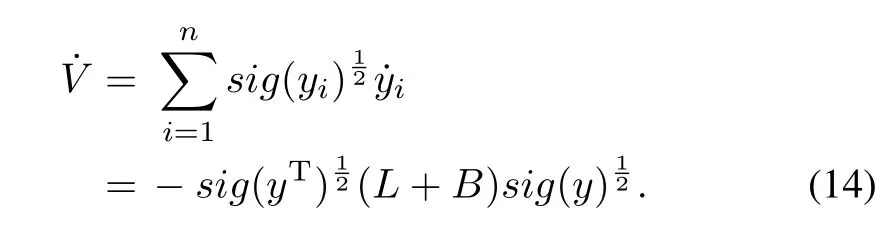
According to Lemma 1,one has thatL+Bis positive de fi nite as long asbi/=0 for at least one DG.Denote thesmallest eigenvalue ofL+Basλ1(L+B).Suppose thatV /=0,i.e.,y/=0.Thus,we have

B.Distributed Secondary Frequency Control
The frequency droop characteristic is given by

whereωniis the primary frequency control reference andmPiis the frequency-active power droop coef fi cient.The secondary frequency control is to design the control referenceωnisuch that the frequency of each DG synchronizes with the nominal valueωref.Differentiating(20)yields

whereµiis an auxiliary controller to be designed.Similar to the distributed voltage control problem,the distributed frequency control problem can be transformed into the following leader-following problem

Let the auxiliary control input be
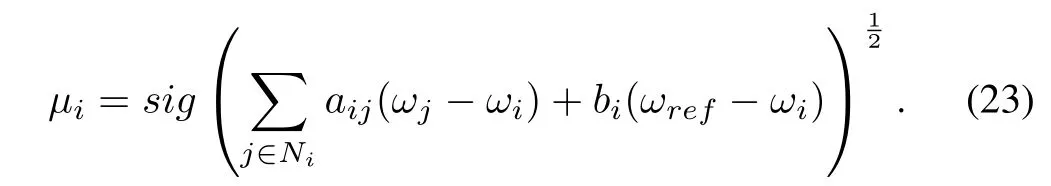
Applying the same analysis as that in the proof of Theorem 1,we get the following result.
Theorem 2.Consider the secondary frequency control system(21).Let the communication topology be connected andbi/=0 for at least one DG.Under the auxiliary control inputµigiven in(23),the output frequencyωiof each DG synchronizes with the reference valueωrefin fi nite time.
Remark 2.The distributed secondary voltage and frequency control schemes are motivated by the cooperative control theory of multi-agent systems[15-18].The droop-based primary control will cause the voltage and frequency deviations from nominal values once a microgrid is islanded.The proposed secondary control schemes can restore the voltage and frequency to their nominal values in fi nite time.
IV.DISTRIBUTED AND OPTIMAL ACTIVE POWER SHARING SCHEME
To minimize the total cost of generation while satisfying system active-power balance requirement,we need to schedule each generator’s active power output.The generation cost for thei-th generator can be approximated by[21]
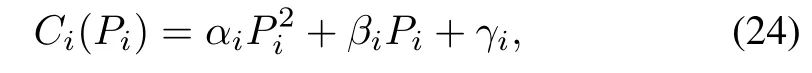
whereαi,βi,andγiare the cost parameters.Optimization of generation cost in microgrids can be described as
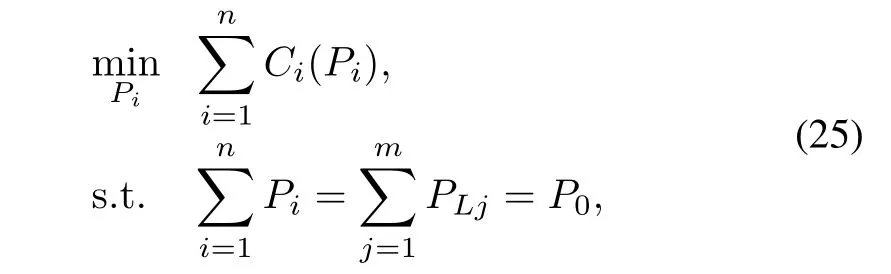
wherePLjis the power consumed by the loadjandP0denotes the total load in microgrid.The Lagrange function for the optimal problem in(25)can be written as
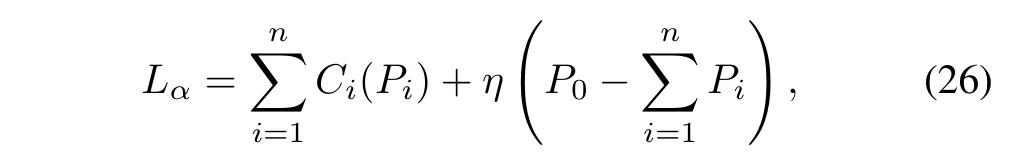
whereηis the Lagrange multiplier.
From the fi rst order optimality conditions,we have
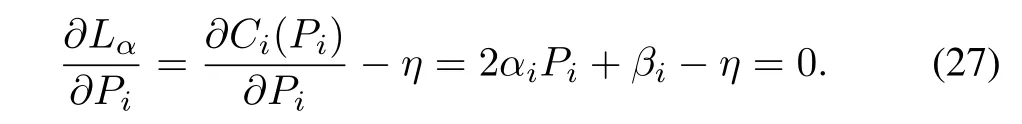
According to(27),we get the following optimal solution

i.e.,the optimal dispatch corresponds to the dispatch for which the incremental cost of each generator is equal toη∗.
From(28),we have
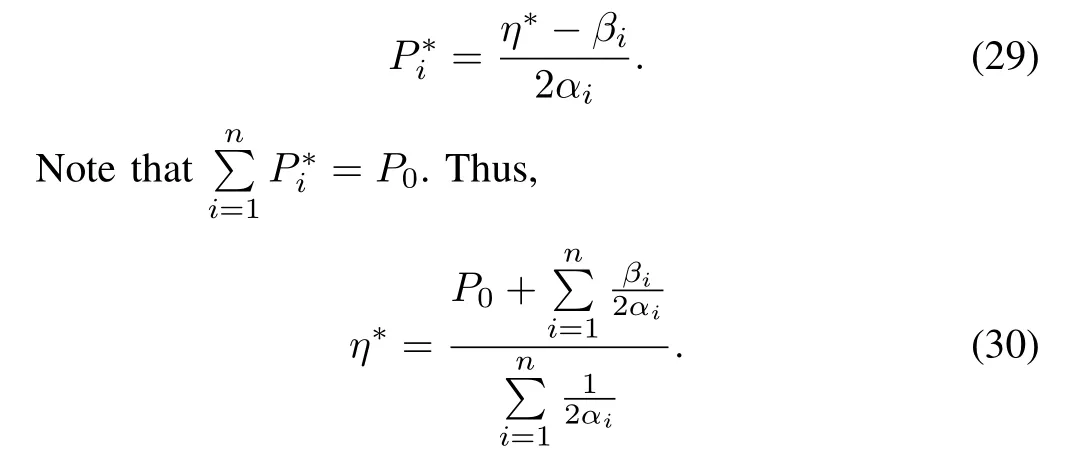
From(30),we see that the optimal value is related to the entire network information.Consider that the microgrid structure is fully distributed.This optimal value cannot be calculated directly.In what follows,we provide a distributed algorithm to solve the optimal problem(25).We fi rst introduce some auxiliary variablesζiand consider the following transformation
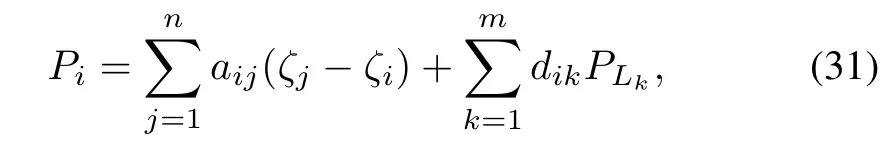
whereaijdenotes the weight of the edge between the generatoriandjanddikrepresents the weight of the edge between the generatorsiand the loadk.dik=1 if the loadkis in the neighborhood of the generatorianddik=0 otherwise.The cyber network is constructed so that a load just communicates with one of the nearest generator.Thus,
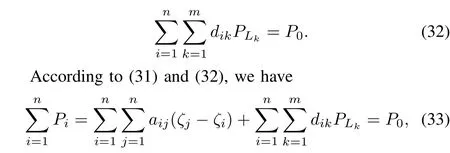
which implies the constraint in(25)is satis fi ed.
Now we are ready to present one of the main results. The following distributed algorithm is proposed to solve the optimal dispatch problem(25).

Theorem 3.Let the communication topology among the DGs be connected.The distributed algorithms(34)-(37)solve the optimal dispatch problem(25),i.e.,ηi→η∗andPi→(i=1,2,...,n)exponentially.Moreover,the exponential convergence rate is not worse than
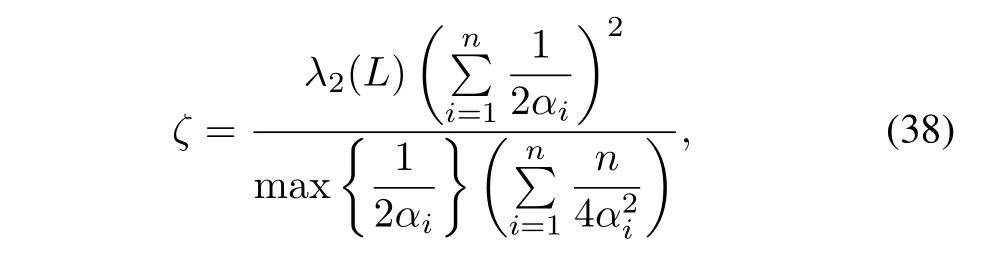
withλ2(L)denoting the smallest nonzero eigenvalue ofL.
Proof.According to(34)and(36),we have

Furthermore

withλ2(L)denoting the smallest nonzero eigenvalue ofL.The norm of¯δis‖¯δ‖=‖δ‖cos(θ)withθbeing the angle between the vectorsδand¯δ.Sinceθis not greater than the dihedral angleψwhich is equal to the angle between the normal vectors

It is shown that the disagreement vectorδexponentially vanishes with a speed of at leastζ.□
To achieve the optimal active power generation in microgrid, we introduce another auxiliary control inputτi


V.SIMULATION STUDIES
The effectiveness of the proposed control scheme is veri fi ed by simulating an islanded microgrid in Matlab/SimPowerSystems.Fig.3 gives a microgrid test system.This microgrid consists of four DGs.The parameters of the test system are shown in Table I.
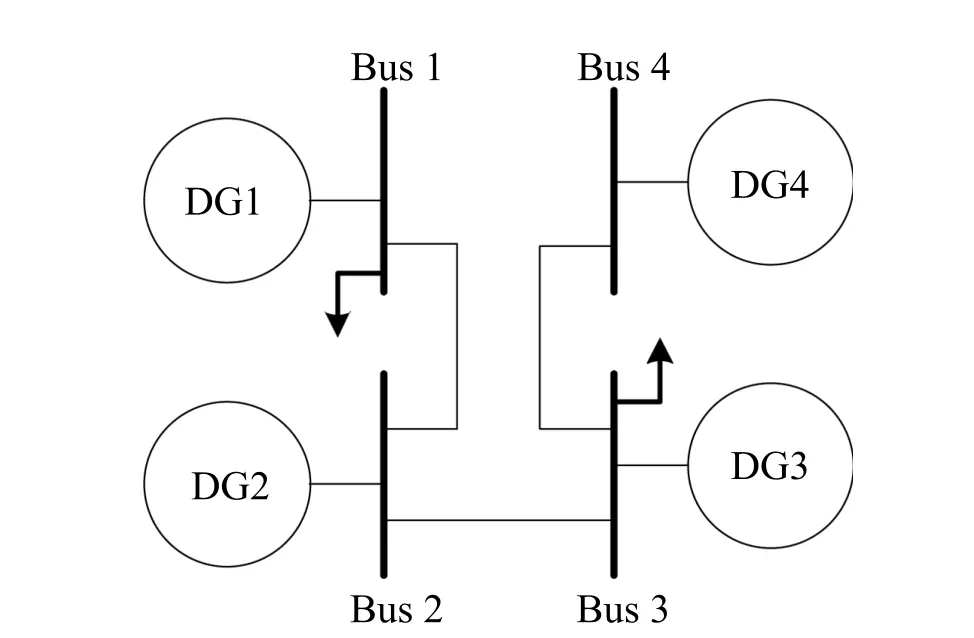
Fig.3.Block diagram of the microgrid test system.
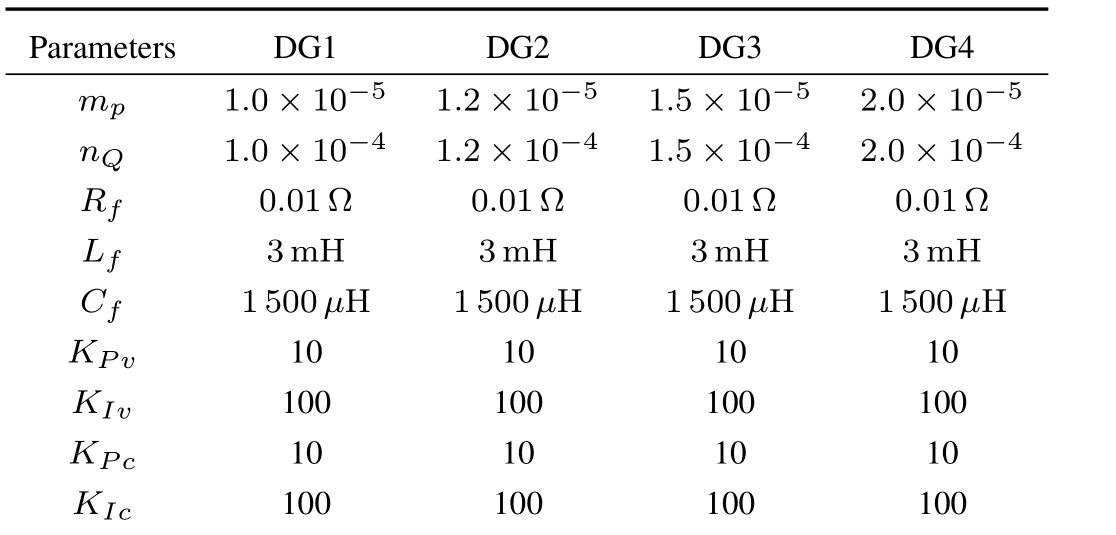
TABLE I PARAMETERS OF THE MICROGRID TEST SYSTEM
It is assumed that the DGs communicate with each other through the communication topology depicted in Fig.4.The communication topology is chosen based on the geographical location of DGs.The associated adjacency matrix of the graph in Fig.4 is

DG1 is the only DG that is connected to the virtual leader node with the pinning gain ofb1=1.
The cost parameters for the DGs are given in Table II.We fi rst calculate the optimal active power generation values for each DG.According to the centralized optimal solution shown in(30),we get the optimal incremental costη∗=16.15$/kW. The corresponding optimal active power outputs for the DGs are as follows:=79.44kW,=81.69kW,=64.88kW,and=73.99kW.Next we utilize the distributed optimal dispatch algorithm to solve this economic dispatch problem.Assume that this algorithm is activated att=5s.Fig.5(a)shows the incremental costsηi.It is seen that the incremental costsηiconverge to the same value 16.15.That is,we get the exact optimal solutions by using the proposed distributed algorithms.Fig.5(b)shows that the active power generation references exponentially converge to the optimal values.

Fig.4.Communication topology 1.

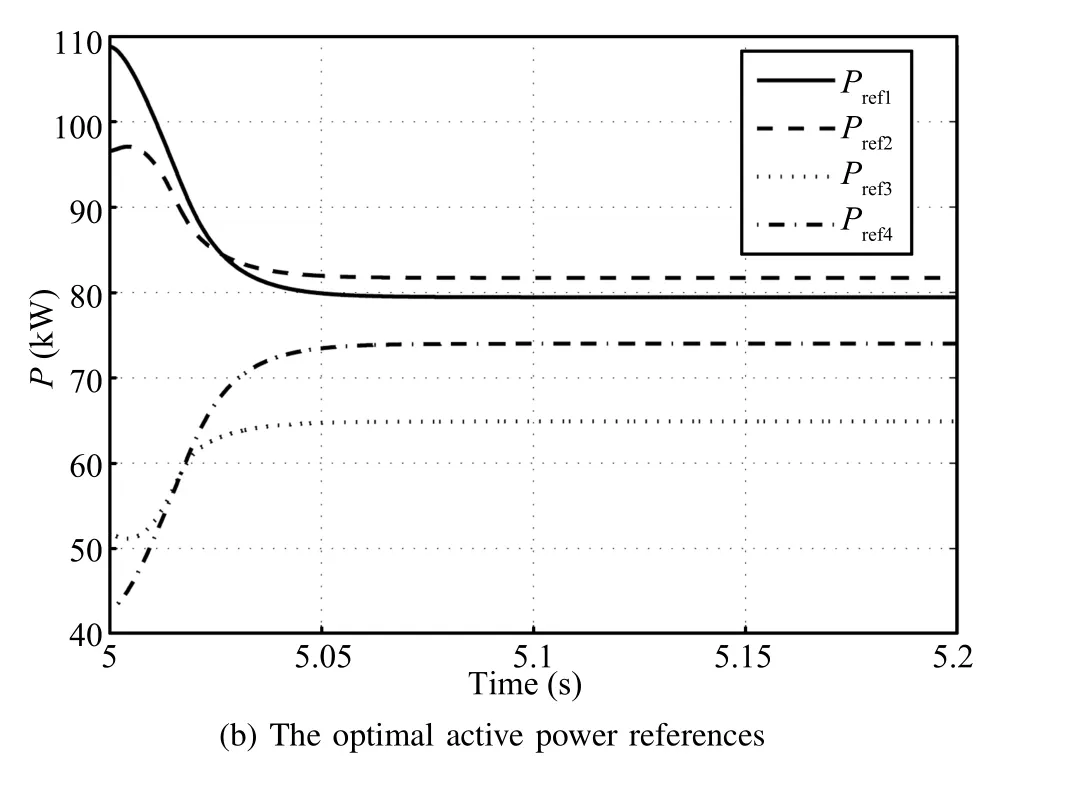
Fig.5.Distributed solutions for optimal active powers.
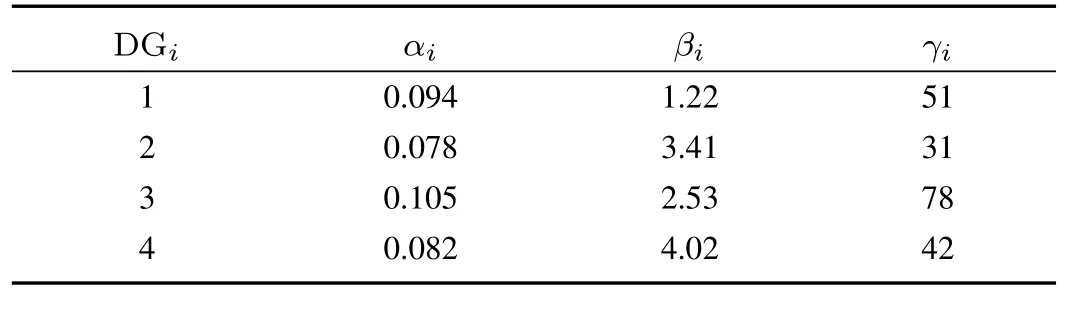
TABLE II THE DG COST PARAMETERS
The nominal values for the terminal voltagevrefof DGs and the frequencyωrefare set as 380V and 314.16rad/s, respectively.It is assumed that the microgrid is operated in an autonomous mode.Firstly,only the primary controllers are used.As seen from Fig.6,the values of the direct terms of the DG output voltagevodiand the DG terminal voltage amplitudevoiare less than the nominal referencevref.The primary voltage controller cannot avoid the deviations from the nominal values.To regulate the microgrid voltage to the nominal values,the distributed secondary voltage controllers are utilized att=3s.The direct and quadratic terms of the DG output voltages,vodiandvoqi,synchronize with the nominal values 380V and 0V in fi nite time,respectively.The DG terminal voltage amplitude returns to 380V ast≥3.5s.Fig.7 shows the frequency of each DG before and after applying the distributed secondary frequency control.As seen from Fig.7, once the proposed secondary frequency controller is applied, the operating frequencies of the DGs converge toωrefast≥3.5s.Fig.8 gives the active power outputs of the DGs. Although the demand-generation balance is guaranteed,theactive power outputs of the DGs are not optimal before the optimal dispatch algorithms are activated.After the optimal dispatch algorithms are applied,we can see that the DG active power outputs converge to the optimized references in fi nite time.

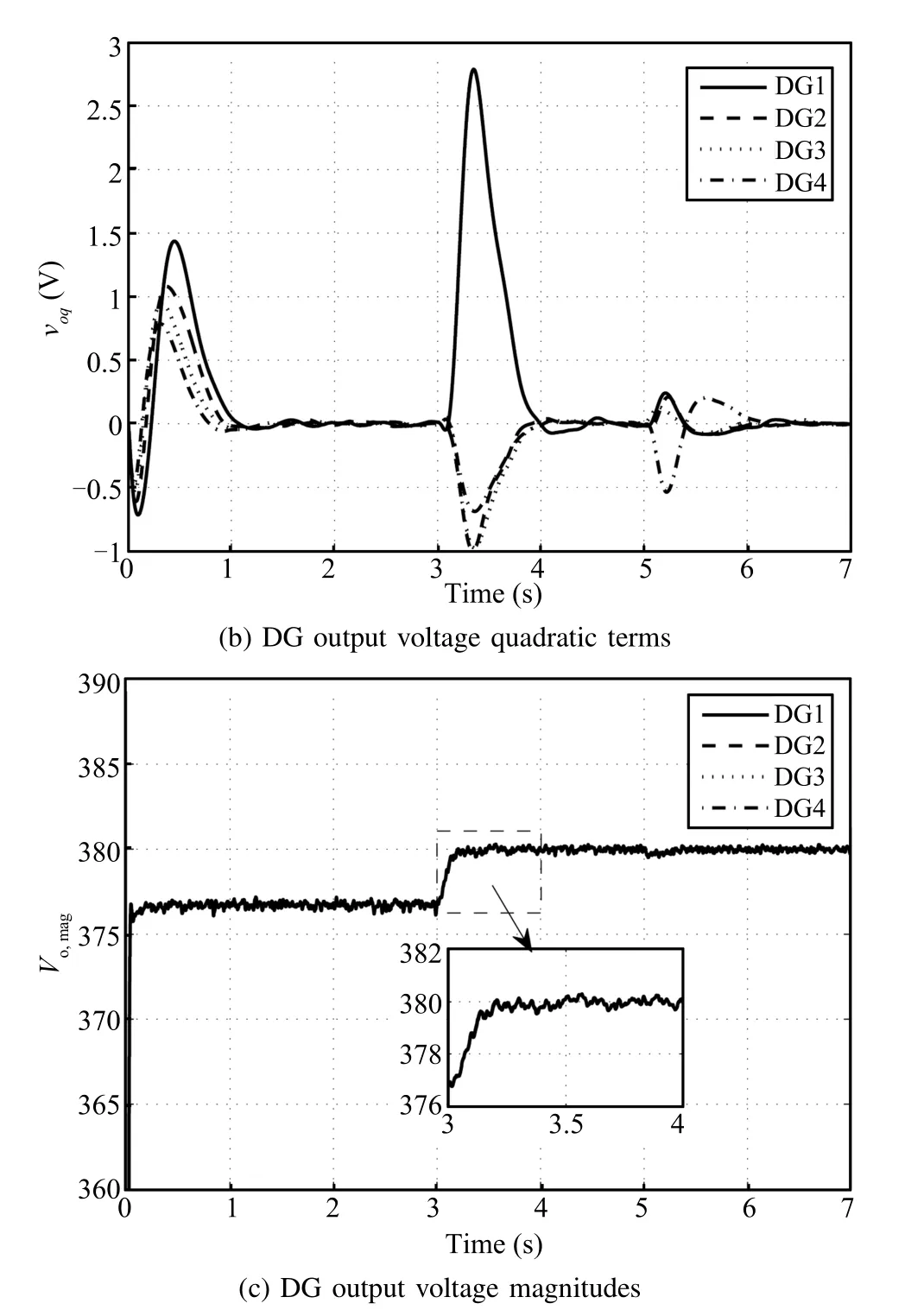
Fig.6.DG output voltage values.
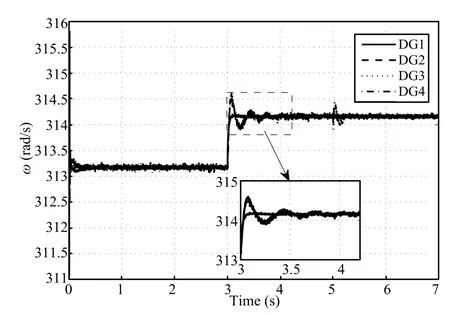
Fig.7.The frequency of each DG.
In the above case,the parameterαin the secondary controllers is set as 1/2 such that the fi nite-time convergence is achieved.To give a comparison,another set of simulation is made under the same parameter settings except that the parameterαis set as 1.In this case,only the asymptotical convergence property is guaranteed.The tracking performance is shown in Fig.9.Compared with Fig.6(c)and Fig.7,the tracking performance has become slower.

Fig.8.The active power output of each DG.
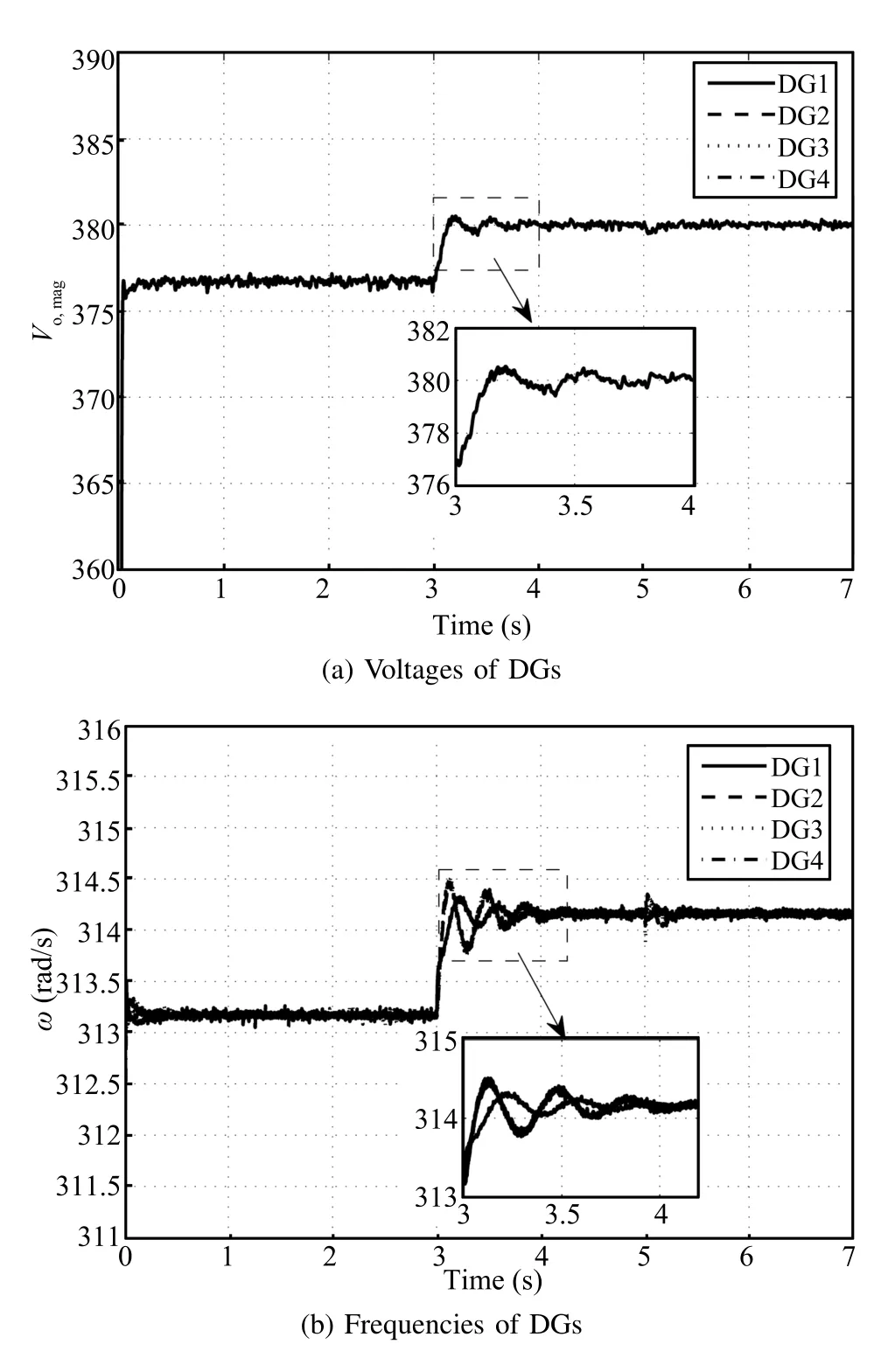
Fig.9.The asymptotical tracking performance.
The communication topology also affects the tracking performance of the secondary control systems.We assume that only DG2 has access to the reference trajectory.Fig.10 shows the communication topology.Under this scenario,the voltage output is given in Fig.11.The convergence performance is different from Fig.6(c)because of the change of the smallest eigenvalueλ1(L+B)for the Laplacian matrixL+B.

Fig.10.Communication topology 2.

Fig.11.The voltage tracking performance.
VI.CONCLUSION
A new control structure for autonomous microgrid was proposed in this paper.The distributed secondary voltage control module,the optimal active power sharing module, and the distributed secondary frequency control module were proposed to enable plug-and-play functionality of microgrids. The whole system was fully distributed such that each generator only requires its own information and the information of its neighbors.Different from the previous work,the optimal power sharing properties of the primary droop controllers are achieved and the satisfactory dynamic performances of the secondary controllers are guaranteed.
REFERENCES
[1]Lasseter R H,Paigi P.Microgrid:a conceptual solution.In:Proceedings of the 35th IEEE Annual Power Electronics Specialists Conference. Aachen,Germany:IEEE,2004,6:4285-4290
[2]Lasseter R H,Piagi P.Control and Design of Microgrid Components. Project Report,New York:Power Systems Engineering Research Center Publication,2006.
[3]Chandorkar M C,Divan D M,Adapa R.Control of parallel connected inverters in standalone AC supply systems.IEEE Transactions on Industry Applications,1993,29(1):136-143
[4]Mohamed Y A-R I,El-Saadany E F.Adaptive decentralized droop controller to preserve power sharing stability of paralleled inverters in distributed generation microgrids.IEEE Transactions on Power Electronics,2008,23(6):2806-2816
[5]Pogaku N,Prodanovi M,Green T C.Modeling,analysis and testing of autonomous operation of an inverter-based microgrid.IEEETransactions on Power Electronics,2007,22(2):613-625
[6]Peas Lopes J A,Moreira C L,Madureira A G.De fi ning control strategies for microgrids islanded operation.IEEE Transactions on Power Systems, 2006,21(2):916-924
[7]Li Y W,Kao C N.An accurate power control strategy for power electronics-interfaced distributed generation units operating in a lowvoltage multibus microgrid.IEEE Transactions on Power Electronics, 2009,24(12):2977-2988
[8]Marwali M N,Jung J W,Keyhani A.Stability analysis of load sharing control for distributed generation systems.IEEE Transactions on Energy Conversion,2007,22(3):737-745
[9]Biddram A,Davoudi A,Lewis F L,Qu Z H.Secondary control of microgrids based on distributed cooperative control of multi-agent systems.IET Generation,Transmission and Distribution,2013,7(8):822-831
[10]Guerrero J M,Vasquez J C,Matas J,de Vicu˜na L G,Castilla M. Hierarchical control of droop-controlled AC and DC microgrids-a general approach toward standardization.IEEE Transactions on Industrial Electronics,2011,58(1):158-172
[11]Savaghebi M,Jalilian A,Vasquez J C,Guerrero J M.Secondary control scheme for voltage unbalance compensation in an islanded droopcontrolled microgrid.IEEE Transactions on Smart Grid,2010,3(2):797-807
[12]Simpson-Porco J W,D¨or fl er F,Bullo F.Synchronization and power sharing for droop-controlled inverters in islanded microgrids.Automatica, 2013,49(9):2603-2611
[13]Ilic M D,Liu S.Hierarchical Power Systems Control:Its Value in a Changing Industry.London:Springer,1996.
[14]Xin H H,Qu Z H,Seuss J,Maknouninejad A.A self-organizing strategy for power fl ow control of photovoltaic generators in a distribution network.IEEE Transactions on Power System,2011,26(3):1462-1473
[15]Ren W,Beard R W.Distributed Consensus in Multi-vehicle Cooperative Control.Berlin:Springer,2008.
[16]Chen G,Lewis F L,Xie L H.Finite-time distributed consensus via binary control protocols.Automatica,2011,47(9):962-1968
[17]Chen G,Yue Y L,Lin Q.Cooperative tracking control for networked Lagrange systems:algorithms and experiments.Acta Automatica Sinica, 2014,40(11):2563-2572
[18]Chen G,Lewis F L.Distributed adaptive tracking control for synchronization of unknown networked Lagrangian systems.IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2011,42(3):805-816
[19]Hardy G H,Littlewood J E,P´olya G.Inequalities.Cambridge:Cambridge University Press,1952.
[20]Bhat S P,Bernstein D S.Finite-time stability of continuous autonomous systems.SIAM Journal on Control and Optimization,2000,38(3):751-766
[21]Wood A J,Wollenberg B F.Power Generation,Operation,and Control. New York,NY,USA:Wiley,1996.

received his Ph.D.degree in control engineering from Zhejiang University,China,in 2006.From 2009 to 2010,he has been a visiting scholar with the Automation and Robotics Research Institute,University of Texas at Arlington.He is currently a professor at the College of Automation, Chongqing University.His research interests include distributed control,cooperative control,intelligent control,cyber-physical system,power system,nonlinear control and control applications.Corresponding author of this paper.
Manuscript received October 8,2014;accepted March 10,2015.This work was supported by National Natural Science Foundation of China(61273108), the Fundamental Research Funds for the Central Universities(106112013CDJZR175501),and the Scienti fi c Research Foundation for the Returned Overseas Chinese Scholars,State Education Ministry.Recommended by Associate Editor Jiming Chen.
:Gang Chen,Ening Feng.Distributed secondary control and optimal power sharing in microgrids.IEEE/CAAJournalofAutomaticaSinica, 2015,2(3):304-312
Gang Chen and Ening Feng are with the Key Laboratory of Dependable Service Computing in Cyber Physical Society of Ministry of Education and the College of Automation,Chongqing University,Chongqing 400044,China (e-mail:chengang@cqu.edu.cn;fengening@cqu.edu.cn).
Ening Feng graduated from Xinyang Normal University,China,in 2012.He is currently a master student at the College of Automation,Chongqing University.His research interests include cooperative control,cyber-physical system,and power system.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- End-to-end Delay Analysis for Mixed-criticality WirelessHART Networks
- An Algebraic Detection Approach for Control Systems under Multiple Stochastic Cyber-attacks
- A Stochastic Programming Strategy in Microgrid Cyber Physical Energy System for Energy Optimal Operation
- Cost Minimization of Wireless Sensor Networks with Unlimited-lifetime Energy for Monitoring Oil Pipelines
- Water Supply Networks as Cyber-physical Systems and Controllability Analysis
- Guest Editorial for Special Issue on Cyber-Physical Systems
