具有不确定内部干扰的薛定谔系统的追踪控制

刘 镇，崔皓月

(天津大学数学系，天津300072)

近几年来，追踪控制一直是国际工程学和应用数学领域的一个热点课题，在军事，生物以及计算机等领域都有广泛的应用.早期对追踪控制的研究大多是在有限维空间内，控制系统用常微分方程描述，这方面的研究已经取得了很好的结果.然而，由于偏微分方程控制系统的复杂性，带干扰的偏微分系统的控制问题一直是控制领域的一个难题.随着无穷维系统理论的日益完善，带不确定干扰的控制问题成为了分布参数系统的研究热点，许多数学家以及工程学者都投入到这方面的研究中.由于系统存在干扰，在研究追踪问题的同时必须考虑干扰的消除.众所周知，在有限维系统中，滑膜控制具有很多优良的特性，比如对系统的鲁棒性.此外，选择合适的滑模面可以大大降低控制器设计的困难性.因此，滑膜控制广泛应用于抗干扰和追踪控制问题.在文献[1]中Shifman考虑了具有特殊边界条件的欧拉梁系统，通过设计控制器实现了轨迹的渐近追踪.在文献[2]中，Mounier讨论了一类带有载荷的波方程的追踪问题，将其看作线性衰减系统进行考虑，设计了一种新型控制器解决了追踪问题.其他的结果可以参照文献[3-7].

本文将滑膜控制技术应用于无穷维系统中.考虑了带有不确定干扰的薛定谔系统的追踪问题，假定干扰一致有界并且绝对光滑，设计了一种带增益的单位向量控制器追踪指定的目标轨迹，通过构造李雅普诺夫函数的方法证明了追踪误差系统是渐近稳定的，即追踪系统可以渐近追踪到目标轨迹.除此之外，此种控制器设计方法的研究还有着重要的理论价值，可以为解决弹性系统包括弦系统，梁系统等的追踪控制问题以及抗干扰问题提供可行方案.

1 模型建立与控制器设计

本文主要研究一类分布式追踪控制问题，已知目标轨迹的系统信息，且追踪系统内部含有不确定的干扰.

目标轨迹通过如下的偏微分方程描述:

其中:q(x，t)表示时刻在x点处的位移.假定系统在左右端点是固定的.

追踪系统用类似系统(1)的二阶偏微分方程描述:

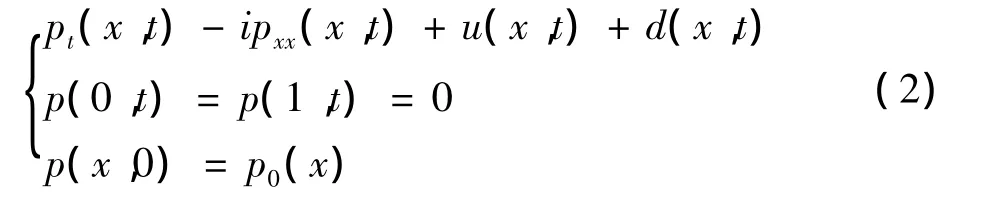
其中:p(x，t)表示t时刻在x点处的位移，u(t)表示控制输入，d(x，t)表示输入干扰，并且d(x，t)满足如下的假设条件.

假设:d(x，t)∈H4，2(0，1)，其中 H4，2(0，1)是索伯列夫空间，并且d(x，t)满足边界条件.dxx(0，t)=dxx(1，t)=0假定d(x，t)是有界的，即存在常数 M1以及 M3使得‖d(x，t)‖2≤M1，‖dxxxx(x，t)‖2≤M3，∀t≥0.

设追踪系统与目标轨迹的误差为:

e(x，t)=p(x，t)-q(x，t)

则追踪误差满足如下方程:

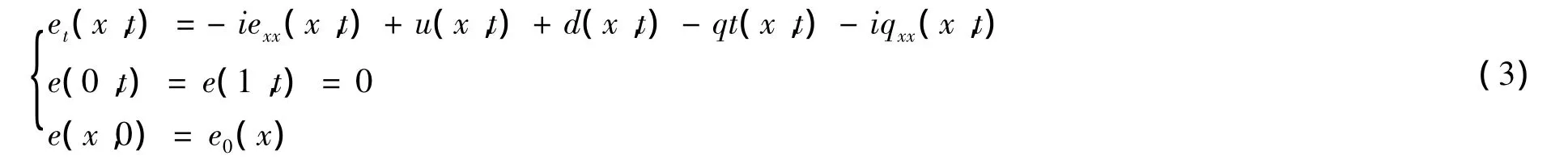
为使误差系统的能量衰减，选取如下控制略:

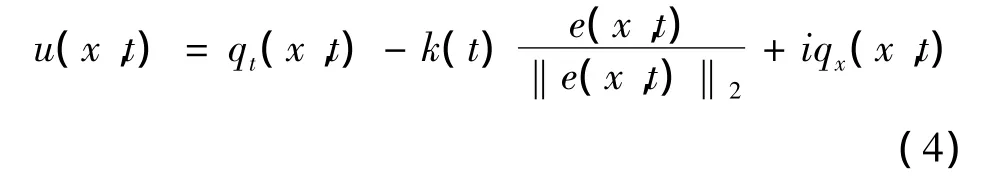
将式(4)带入到式(3)，误差系统变为如下形式:

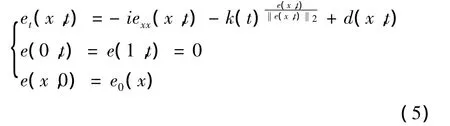
下面，我们只需证明系统(5)是稳定的.

2 系统(5)的稳定性分析

定理1对于追踪误差系统(5)，d(x，t)满足假设条件，则在控制策略(4)下误差系统(5)是渐近稳定的.即系统(1)可以渐近追踪到系统(2).

证明:定义如下的Lyapunov函数:

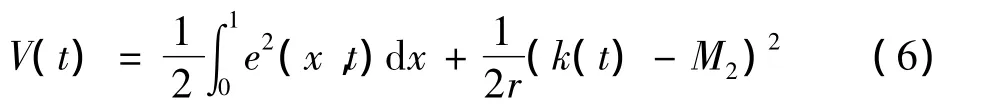
其中:M1＜M2.

对式(6)关于t求导，运用复变函数的知识[8]，分布积分并且利用边界条件计算得

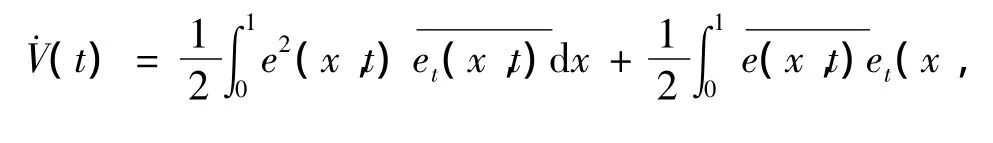
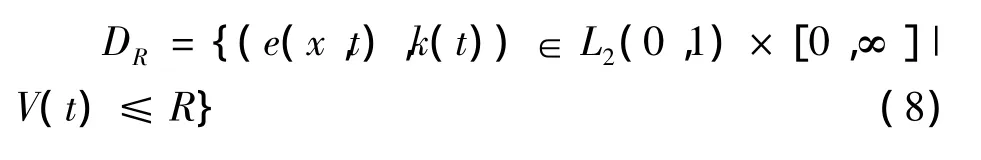
显然，DR是关于误差轨迹的不变集.

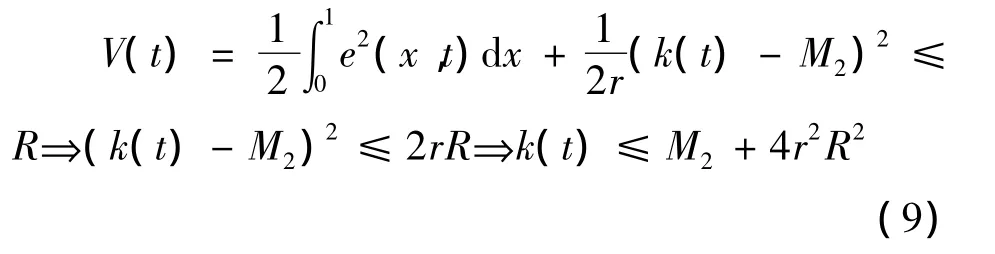
为证明ζ(t)=‖e(x，t)‖2的一致有界性，对t求导得Hölder不等式表明

下一步，将对‖et(x，t)‖2的一致有界性进行讨论，对(5)的第一部分进行估计

设常数M4满足M3＜M4，Lyapunov函数定义为

对 V2(x，t)求导

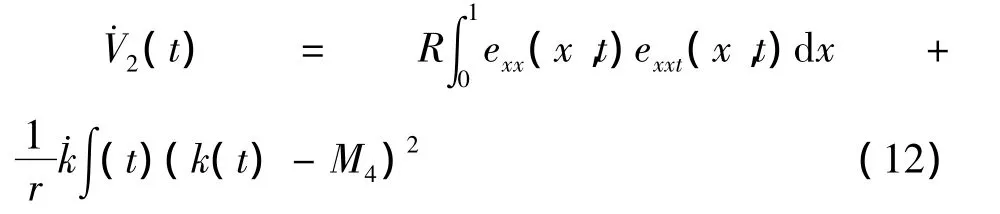
对式(5)求导两次，利用边界条件

根据假设条件对干扰边界的设置，作为式(13)边界条件的补充:

将式(13)带入(12)，有

对于右边的第一项，利用边界条件(14)得

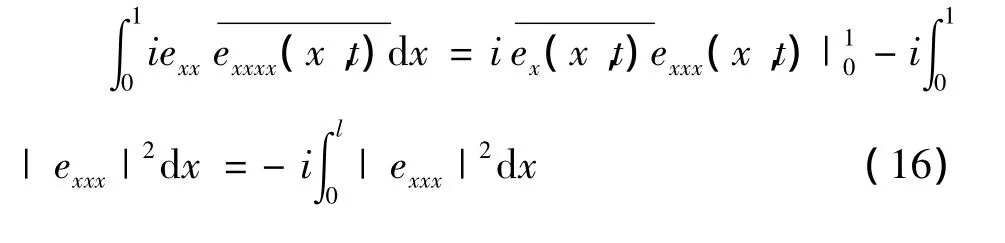
对右边的第三项分布积分两次，利用边界条件以及假设条件

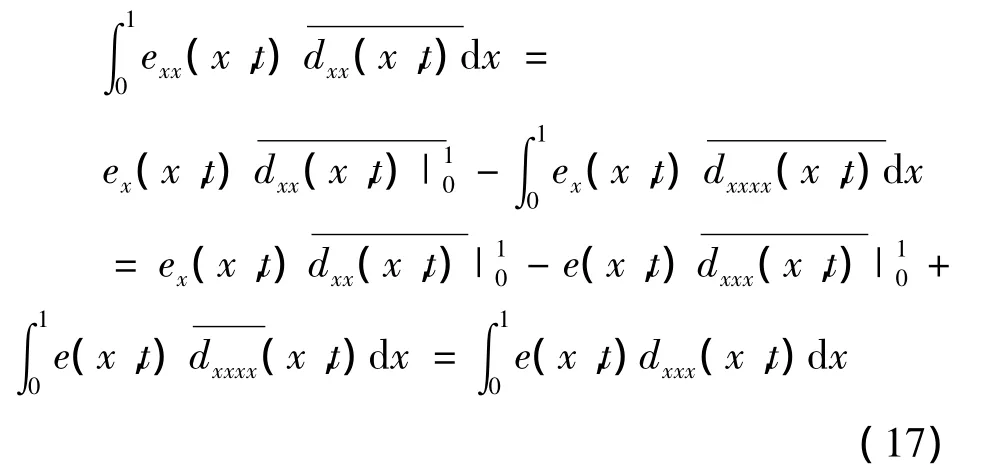
利用Hölder不等式，得

因此Lyapunov函数的导数可以表示为:

引理1 设 z(·)∈H2，2(0，1)是一个标量函数满足 z(1)=z(0)=0，则‖zx‖2≥π‖z‖2，‖zxx(·)‖2≥π‖zx(·)‖2≥π2‖z‖2

由增益k(t)的定义，存在k0使得k(t)≥k0＞0利用引理1对式(19)进行估计

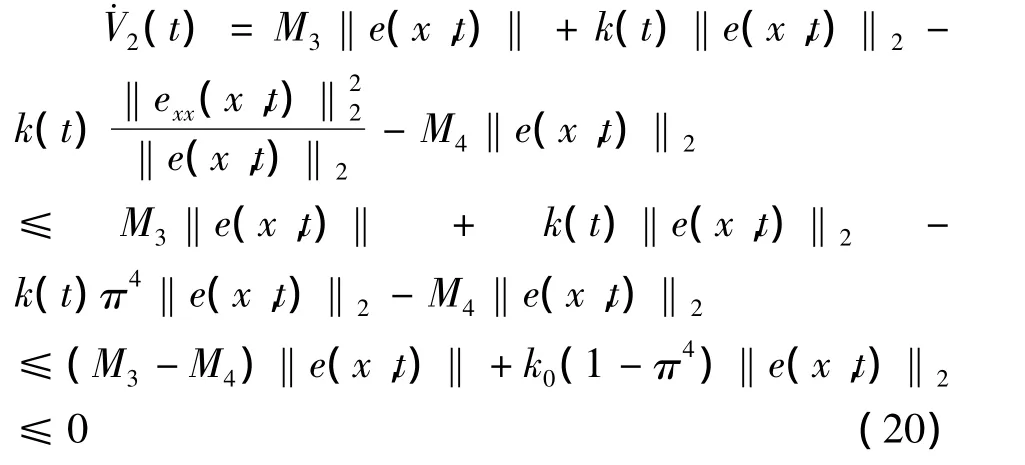
所以V2(t)是半负定的，因此李雅普诺夫函数V2(t)是非增的，对任意的R＞V(0)，设

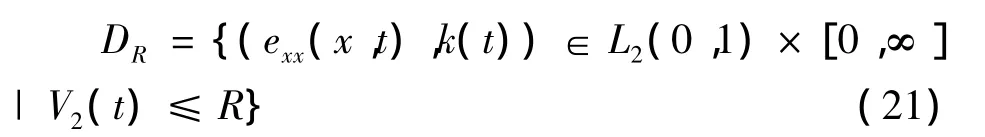
显然是DR是不变集，为证明‖exx(x，t)‖2的一致有界性，有下列的链式估计

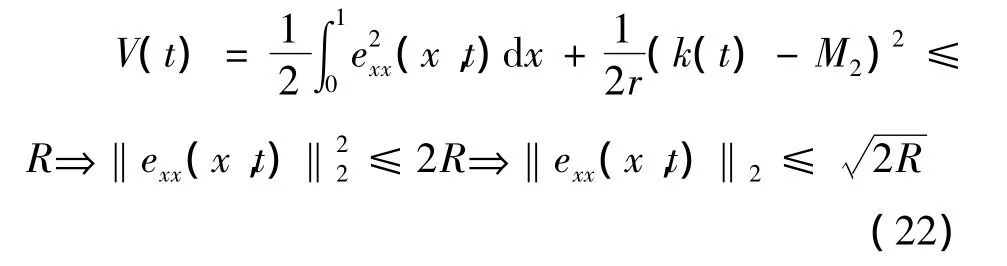
所以‖exx(x，t)‖2是一致有界的.根据式(9)和(10)可以得出et(x，t)是有界的，即存在 ~M，使得‖et(x，t)‖2≤~M.

引理2(Barbalat引理)设x:[0，∞]→R为Lp空间的一个函数，其中p∈[1，∞)，且(t)，t∈[0，∞)，是有界的，那么

根据Barbalat引理可以证明t→∞ 时‖e(x，t)‖2→0.进而，当t→∞ 时，e(x，t)→0，因此误差系统(5)是渐近稳定的，即追踪系统(2)可以渐近追踪到目标轨迹(1).至此，完成了定理1的证明.

3 结语

本文考虑了一类具有不确定内部干扰的薛定谔方程的追踪问题，设计了一个分布式单位向量控制器抵抗干扰.干扰给出合理的假设条件下，通过构造李雅普诺夫函数给出了误差系统是渐近稳定的，即追踪系统可以渐近追踪到目标轨迹.今后的工作是如何将本控制策略推广到其他弹性系统，例如波方程，梁方程等.

[1]SHIFMAN J J.A Tracking Controller for the Euler-Bernoulli Beam[C]//IEEE International Conference on Robotics and Automation，Cincinnati，OH，1990.

[2]MOUNIER H，RUDOLPH J，FLIESS M，et al.Tracking control of a vibrating string with an interior mass viewed as delay system[J].ESAIM，Control，Optimization and Calculus of Variations，1998，3(1):315-321.

[3]MEURER T，KUGI A.Tracking control design for a wave equation with dynamic boundary conditions modeling a piezoelectric stack actuator[J].International Journal of Robust and Nonlinear Control，2011，21(5):542-562.

[4]MEURER T，KUGI A.Tracking control for boundary controlled parabolic PDEs with varying parameters:combining backstepping and flatness[J].Automatica，2009，45(5):1182-1194.

[5]MEURER T，THULL D，KUGI A.Flatness-based tracking control of a piezo actuated Euler-Bernoulli beam with non-collocated output feedback:theory and experiments[J].International Journal of Control，2008，81(3):475-493.

[6]MEURER T，M ZEITZ.Feedforward and feedback tracking control of nonlinear diffusion convection-reaction systems using summability methods[J].Industrial and Engineering Chemistry Research，2005(44):2532-2548.

[7]DIECI L，LOPEZ L.Sliding motion in filippov differential systems:theoretical results and a computational approach[J].SIAM J.Numer.Anal.，2009，47(3):2023 – 2051.

[8]钟玉泉.复变函数论[M].北京:高等教育出版社，1988.121-125，201-204.