从一道概率题谈起
2015-08-04周海燕
周海燕
有这样一道题:“一道选择题共有四个选择答案,其中只有一个答案是正确,小明因不会做此题,就随意选了一个答案,小明做对此题的成功率是多少?”分析:由于一道选择题有四个答案,其中只有一个正确答案,随意选一个答案做对本题成功率25%。解:P(答对)=25%.用到的知识点为:概率=所求情况数与总情况数的比。以上是运用古典概型的方法来解的,但在实际过程中,如果是一次考试,是不是就是25%呢。这就是一个很复杂的问题,这就需要对出卷者和做卷者进行研究了。
首先我们来研究出卷者,出卷者会考虑到很多考生都要猜的,除非绝顶高手。你不猜你就吃亏。而出卷者知道这一点,所以也鼓励大家猜, 当然也要体现公平的原则,即让大家猜到的可能性较小, 最好是平均 25%, 甚至因为心理因素而低于 25%。所以很多题目出好后,要把答案打乱,使正确答案平均分配。特别是现在的中考或高考有的可能运用计算机程序进行设计,尽可能的将几种常见序列猜中的可能性大大低于 25% 的。这时,只有单选某一项,如全A, 全 B, 全 C, 或全 D, 这样猜中的可能性就是 25%,减少瞎猜猜对的可能性,增加考试的公平。
我们再来说答卷者,他每道题都可以随便选四个选项,但他也不是真的随便选,他们也会看一下这四个选项,然后凭感觉随便猜一个(感觉比胡猜好得多),这种方法虽然比胡猜花的时间多一点,但稍微增加了它的猜中率。甚至有的考生在解题时发现这样选C选项的越来越多,同学中有了出现全选C的“C王”, 所以近些年专家们觉得比较好的答案分配是: 23℅, 23℅,28℅, 26℅。 从这个角度讲,现在猜 C 比较好。但也有的学生他不是全不会,可能会排除已知的错误选项,也有的就能正确答出的,他们就根据各个选项所占的比例为25%来猜想,这样也大大的提高了猜中的概率。有及个别的题目甚至出现猜中率为100%。还有学生用自制的四面体骰子随机的抛掷,掷到谁就是谁。还有些学生运用一、两句话用笔随机的点,这还取决于从哪个选项开始,和那一、两句话的字数来确定成功率。还有的用掷骰子的方法来“解答”选择题.如在某次单元测验卷上,小明共有两道选择题不会,每题都有四个选项,且恰有一项是符合题意的.小明准备抛掷一枚质地均匀的正方体骰子来确定“答案”.并作规定:若掷得1、2、3、4点,则分别代表A、B、C、D;若掷得5、6点,则无效并重新抛掷.我们可以用“画树状图”的方法求出小明两道题都碰对概率.
【分析】根据有两道题目,相当于分两步事件,利用树状图法列举出即可.
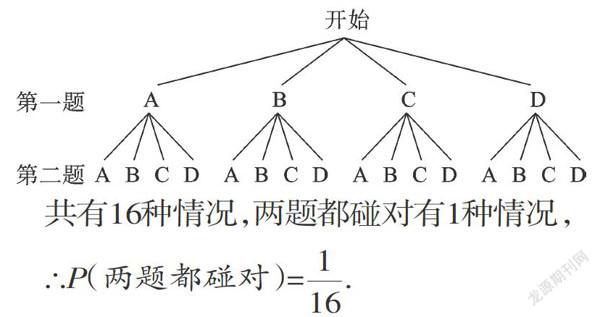
【解析】再如2013年南京市中考题中也出现类似的题目:某次考试有6道选择题,每道题所给出的4个选项中,恰有一项是正确的,如果小明从每道题的4个选项中随机地选择1个,那么他6道选择题全部选择正确的概率是( )
(A) 1 4 (B) ( 1 4 )6 (C) 1( 1 4 )6 (D) 1( 3 4 )6
正确选项是B,这就是说,如果全部靠猜题的话,猜中的概率是很低很低的。
也许专家们和考生之间永远在战斗。专家在将来一定也会改变策略。我个人认为无论怎么改,总有一些考生会比较幸运,专家们能做的,是尽量减少平均猜中率,这是对会做的人的奖赏。此外,可以设计不鼓励猜题的选择题型,这样使选择题型可能更公平,比如答对得四分,不答一分,答错零分。但是在可操作性等方面都值得研究。
