基于蚁群算法的单克隆菌落挑选仪路径规划

邱实　程金光　张荣福

摘要： 单克隆菌落挑选仪是集光学成像、图像识别和自动控制等技术于一身，应用于生物工程领域的一种高端仪器。对12×8阵列挑选针和无序排列的菌落目标，只有对挑选路径和顺序进行优化，才能有效提高挑选通量。针对这一需求，利用蚁群算法的基本原理，对单克隆菌落挑选仪挑选路径进行了优化。仿真实验结果表明，该算法可以有效提高挑选效率。

关键词： 蚁群算法； 信息素策略； 能见度

中图分类号： TP 391.4文献标志码： Adoi： 10.3969/j.issn.10055630.2015.03.016

Abstract： The highthroughput monoclonal colony selection instrument is a highend equipment applied to biological cell engineering which contains the technologies of optical imaging， image recognition and automatic control. For the 12×8 probe array and the targets in random order， only the optimization of selected path and order can improve the throughput. Thus， this paper presents the principle of the basic ant colony algorithm and optimizes the selection path based on the algorithm. Then results of the experiment prove the method can greatly improve the selection efficiency.

Keywords： ant colony algorithm； pheromone update strategy； visiability

引言单克隆菌落挑选仪是集光学成像、图像识别和自动控制等技术于一身，应用于生物工程领域的一种高端仪器，在我国处于起步研制阶段。在经过诱变和培养的数以万计的菌株中，仅有百分之几是符合要求的高性能菌株。传统的挑选菌株方式是通过目视菌落形态颜色等特征，人工方式取出优质菌株，该方法不仅重复性差，而且效率极低。为了提高挑选效率和可靠性，美国、德国、瑞士等国相继开发出基于光学成像和图像识别技术的单克隆菌落挑选仪。其工作原理是对菌落图像进行分析，通过分析菌落形态、大小、圆度、长短径比和颜色等特征，进而标记出高性能菌落[12]，并利用机械手带动探针实现菌落的挑取和转移。单克隆菌落挑选仪的一个重要考核指标是单位时间内能完成的操作数量（即通量），通量与机械手行走的路径直接相关。因此为了实现高通量，需要找到最科学合理的挑选路径，这也是仪器研发面临的重要问题之一。图1菌落挑选仪探针阵列

Fig.1Probe array on selection instrument菌落挑选仪探针阵列如图1所示，机械手末端为12×8的探针阵列，菌落目标则随机分布在圆形培养皿区域内。随机械手移动到相应位置，探针逐一伸出，每根探针挑取一个目标后，一次性放入标准96孔深孔板。在设计初期，每次挑选匹配间隔距离最小的探针和菌落目标，以期通过减小单次运动量缩短总路径长度，该方法称为最近点法。最近点法是一种贪心算法，单次运动量对路径优化具有启发性，但不是决定性的。针对这一典型的组合优化问题，本文使用蚁群算法进行优化。

1蚁群算法及其在路径优化中的实现

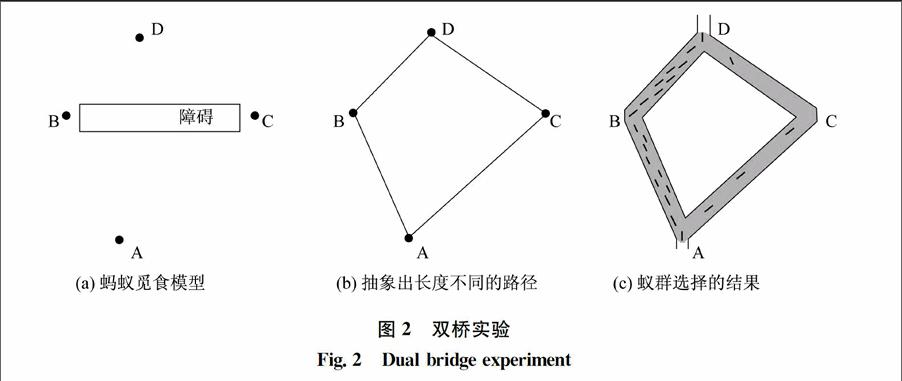
1.1蚁群算法蚁群算法是一种模拟蚂蚁群体觅食行为的仿生优化算法[3]，觅食过程中，虽然每只蚂蚁的智能和认知水平有限，但是通过个体与个体之间基于生物化学物质的通信，相互影响，最终能适应苛刻的环境，解决复杂的问题，这是一种群体智能。图2为反映群体智能的双桥实验。

如图2（a）所示蚁穴A与食物D之间存在障碍，起初蚁穴中的蚂蚁随机地寻找能绕过障碍搬运食物的路径，同时在这些路径上留下能被同伴嗅觉捕捉的信息素。不同的路径长度不一，如图（b）中的ABD、ACD，蚂蚁往返在较短的路径上将留下更多的信息素，随着信息素的浓度的差异，大多数的蚂蚁将选择较短的路径如图（c）所示。蚁群算法即仿照蚂蚁群的这种行为特征，利用一组数据作为算子间通信的生物信息素，启发算法进行寻优搜索，可以解决复杂的组合优化问题。假设有n个目标地点，开始有m只蚂蚁随机地分布在n个地点上，记t时刻i到j的路径lij上的信息素强度为τij（t），在t+1时刻，m只蚂蚁各自向下一目标移动，为了防止蚂蚁反复经过同一目标，需设置禁忌表tabu，记录已经去过的目标，随移动进程变动。蚂蚁k在t时间内选择i到j的路径lij的概率可以根据路径上的信息素计算出[4]Pkij（t）=[τij（t）]α·[ηij（t）]β∑sallowedk[τis（t）]α·[ηis（t）]βjallowedk

0else（1）式中：allowedk表示蚂蚁k下一步允许选择的目标，即全部目标集合C减去k的禁忌表集合；α为信息启发因子，表征信息素在路径选择时的作用；β为期望启发因子，表征距离启发因素（能见度）在路径选择时的作用；ηij为启发函数，是路径长度dij的倒数。每次蚂蚁完成了一条路径，就会更新各处的信息素。遍历过n个城市后在路径lij上的信息素为τij（t+n）=ρτij（t）+Δτij（2）

Δτij =∑mk=1Δτkij（3）式中，ρ为挥发系数，Δτij为在该次移动中由其他蚂蚁留下的信息素，Δτkij为蚂蚁k在路径lij上留下的信息素。根据基本的信息素策略[3]，信息素表达式为Δτkij=QLk第k只蚂蚁经过路径lij

0第k只蚂蚁并未经过路径lij（4）式中，Q为为信息素强度，Lk为蚂蚁走过的长度。

1.2蚁群算法在挑选仪单克隆菌落挑选仪优化中的实现蚁群算法可用在求解旅行商问题，旅行商问题（travelling salesman problem，TSP）即为一名旅行商需要去拜访若干城市，寻找只拜访各城市一次后返回出发点的最短路线的问题。其数学模型描述[5]为C={c1，c2，…，cn}为城市，L={lijci，cjC} 是集合C中元素两两之间的路径集合，dij为lij长度。G=（C，L）是一个有向图，求解旅行商问题是从G中找到长度最短的Hamilton圈。区别于传统旅行商问题，在对挑选仪进行优化时，需要做以下处理：（1）在对挑选仪路径优化时，相对目标移动的不是一个点，而是矩形探针阵列（以下称运动针盘），算法中的每次移动取决于运动针盘上要使用的探针p以及目标菌落t，组合集合C={（p，t）p∈P，t∈T}（P，T分别为96枚探针的集合和96处菌落目标的集合），由于探针和菌落均不重复使用，故约束任意两个C的元素ck=（pi，ti）和cl=（pj，tj），有pi≠pj且ti≠tj。（2）运动针盘安装在正交的二维导轨组成的机械手上，由伺服电机驱动，以脉冲信号控制。在常加速度模式下，伺服电机接收到指定脉冲信号开始以a=0.3 g起步加速，加速至预先设定的工作速率vm，脉冲停止时开始减速刹车[6]。在统计行程时依据机械手运动的两个特点①两条导轨分别由各自电机驱动，定位时间由两条导轨中行程长的一维决定；②电机的行程和时间对应关系可视为为线性关系t=vma+svm。（3）蚁群算法工作建立在个体通信的基础上，对于大规模TSP问题，使用蚁群算法会产生极其庞大的运算开销，本文研究的探针与目标组合数达到了962，完整的信息素记录可能多达几千万组，因此平衡通信开销和搜索空间的充分性是改进蚁群算法的必要工作。算法工作者为改进蚁群算法提出了多种信息素更新策略[7]。在解决本问题时，引入能见度阈值的概念，运动针盘可选路径很多时（如在最开始的几步），决定运动方向前先根据各目标位置进行初步过滤，忽略运动跨度较大的路径上的信息素，这种跨越必然是不合理的。一种阈值设置方法Qd=w（dmin+dmax），其中系数w∈（0，1），dmin、dmax分别为未使用的各探针与各目标的距离的最小、最大值。此外，在算法程序中设置信息素字典动态记录路径被采用的概率，信息素持续挥发值小于一定值时，将此记录删除以节省存储空间。

2模拟仿真实验

2.1实验设计本文根据蚁群算法编写了优化程序，并设计了仿真实验测试优化效果。在直径9 cm的区域内随机生成96个点作为菌落目标，探针排列为12列8行，相邻间隔9 mm，在菌落区域移动仿真图见图3。根据菌落挑选仪在图像捕获时刻的位置关系，将两者初始相对位置设定为常数。目标排列的形状与探针形状相符的程度决定着最优解的大小，极端情况下，目标排列与探针阵列完全相同，则整个挑选过程只需一次移动。为了减少“巧合”造成的影响，实验通过对多组目标优化，分析最优解的收敛情况。

2.2实验结果实验参数[89]中α=2.5、β=4.5、ρ=0.5、Q=400、m=20。绘制出平均路径长度收敛曲线如图4，由图中可见，算法在1次迭代将最优解值收敛到415 mm，在5次内开始优于最近点法，随迭代次数增加，收敛逐渐趋于平缓。图5反映了不同样本分别用最近点法和蚁群算法优化最终结果的差异。经过蚁群算法优化，路径总长度相比最近点法得到进一步缩短，而且没有因样本差异产生显著波动。

3结论本文针对单克隆挑选仪研发中遇到的挑选路径优化问题，结合机械手运动特点，将探针与目标组合，构成抽象城市的概念，根据蚁群算法，对最优挑选步骤进行了启发式优化，并采取适当的信息素策略控制运算规模。模拟实验结果表明，蚁群算法的应用有效地减少了菌落挑选探针的移动距离，从而提高了仪器通量。参考文献：

[1]周莹莉，曾立波，刘均堂，等.基于图像处理的菌落自动计数方法及其实现[J].数据采集与处理，2003，18（4）：460464.

[2]陈东科.加强形态学检查提高细菌鉴定的准确性[J].实验与检测医学，2012，30（5）：419422.

[3]ERIC B，MARCO D，GUY T.Swarm intelligence：from natural to artificial systems[M].Oxford：Oxford University Press，1999.

[4]李士勇，陈永强，李研.蚁群算法及其应用[M].哈尔滨：哈尔滨工业大学出版社，2004.

[5]段海滨.蚁群算法原理及其应用[M].北京：科学出版社，2005.

[6]黄兆斌，黄云龙，余世明.几种步进电机加减速方法的对比研究及其应用[J].机电工程，2011，28（8）：951974.

[7]岑宇森，熊芳敏，曾碧卿.基于新型信息素更新策略的蚁群算法[J].计算机应用研究，2010，27（6）：20802083.

[8]詹士昌，徐婕，吴俊.蚁群算法中有关算法参数的最优选择[J].科技通报，2003，19（5）：381386.

[9]吴春明，陈治，姜明.蚁群算法中系统初始化及系统参数的研究[J].电子学报，2006，（8）：15301533.

（编辑：张磊）