基于MATLAB 的Nomarski棱镜优化设计
2015-08-04李弥高黄敏健胡丽娟
李弥高 黄敏健 胡丽娟
摘要: 根据落射式微分干涉相衬显微镜中Nomarski棱镜的光学原理,通过几何光学运算,推导出棱镜主要结构参数的理论关系式,利用MATLAB程序将关系式转化为二维曲线,再根据关系曲线的变化趋势来确定适合于Nomarski棱镜主要结构的参数取值范围,从而实现优化设计的目的。
关键词: 落射式微分干涉; Nomarski棱镜; MATLAB
中图分类号: TH 742.4文献标志码: Adoi: 10.3969/j.issn.10055630.2015.03.011
Abstract: According to the optical principle of Nomarski prism of the reflected differential interference contrast microscope, the theoretical relationship of the main parameters of the prism structure is derived. By using MATLAB program, the theoretical relationship is transformed into a 2D curve. Then, according to the changing trends of the 2D curve, the parameter range is confirmed which is suitable for the main structure of Nomarski prism. Finally, the optimized design is achieved.
Keywords: reflected differential interference; Nomarski prism; MATLAB
引言随着现代信息产业的发展,落射式微分干涉相衬显微镜的应用越来越广泛,其关键技术之一是Nomarski偏振分光棱镜设计[1]。为了满足显微镜光学与机械系统要求,需对Nomarski棱镜主参数进行优化设计,从而使棱镜相干平面与物镜后焦平面重合,以获取对比度较高的伪浮雕图像。本文基于Nomarski棱镜光学原理,推导出棱镜相干平面高度与棱镜主要结构参数的关系,运用MATLAB程序将理论关系转换成关系曲线,寻求最优化棱镜设计与制造工艺方案,进一步推动落射式微分干涉相衬显微镜产业化发展。
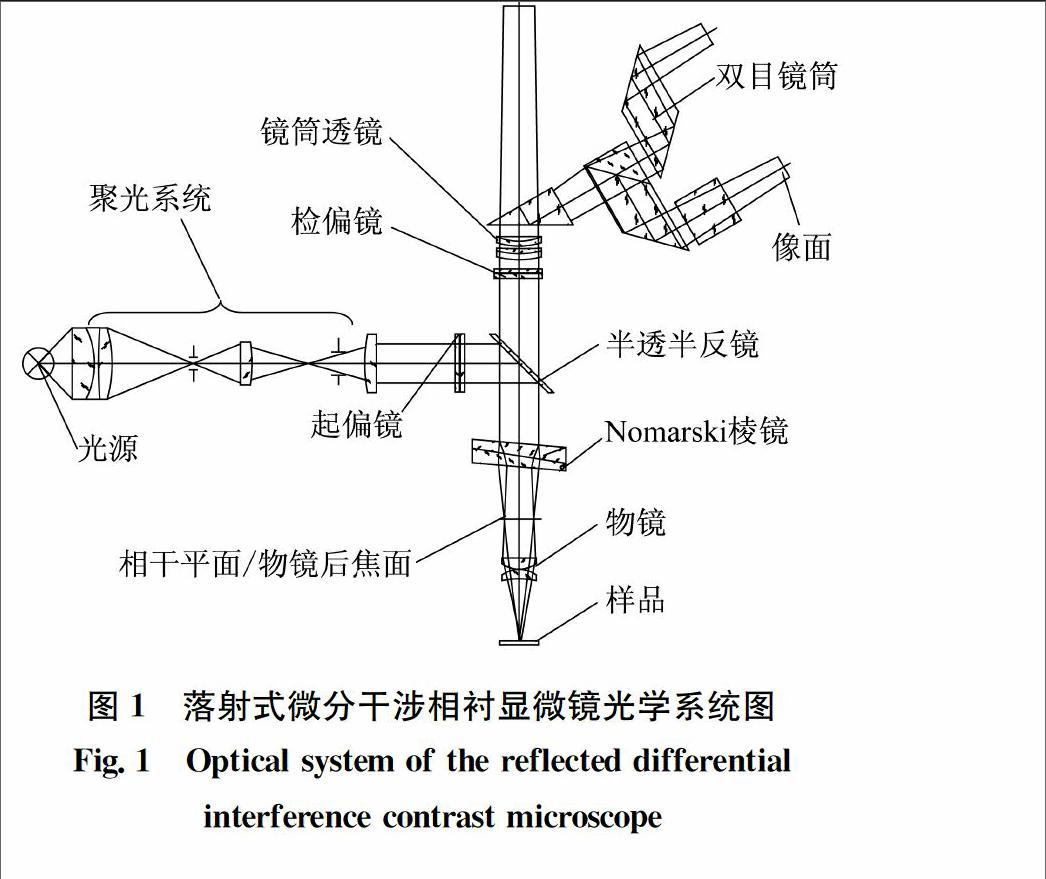
落射式微分干涉相衬显微术的基本原理微分干涉相衬显微术是一种双光束(偏振光)干涉显微术[2],落射式微分干涉相衬显微镜的光学系统如图1所示,从光源发出的光线经过聚光系统后进入起偏器,使光束变为线偏振光,线偏振光经半透半反镜反射,入射到Nomarski棱镜。由于棱镜是由两块单晶且晶轴方向互相垂直的楔形棱镜胶合而成的平板[3],单轴晶体具有双折射特性,可将入射的线偏振光分裂成两束具有某夹角的偏振光,其中一束偏振光的传播速度不随着入射方向的改变而改变,即它的折射率为常数,称为寻常光o光,另一束偏振光的传播速度则随着入射方向的改变而改变,即它的折射率为变数[4],称为非常光e光,o光与e光的振动方向相互垂直,且振幅相等。当两束光波进入胶合面时,原来的e光由于其电矢量振动方向垂直于入射楔镜的光轴,故变为o光;同样原来的o光变成e光,最后从棱镜折射出两束光的交点轨迹重合于棱镜外的某一平面,该平面称之为相干平面。这两束光经过物镜后,产生具有一定剪切量的平行光,落射到被测物体表面。光线经反射,再次进入棱镜以后两束光重新汇合在一起,根据光的干涉原理,两束光波只有在频率相同、位相差稳定、振动方向一致时才会产生干涉现象,因此从样品反射回来经过Nomarski棱镜后的线偏振光,由于偏振方向相互垂直,故不发生干涉。只要用检偏镜将光振动面都投影到同一平面上,两束光就会发生干涉[5]。在微分干涉相衬显微镜中要观察到具有立体感的浮雕像,必须具备下列条件[6]:(1)经Nomarski棱镜和物镜后的两束光波形成的横向剪切量应小于显微物镜的分辨率,从样品表面反射进入物镜与Nomarski棱镜后的两束光波,能将样品中横向分离值的光学梯度以光强衬度表现出来,而成为可见。
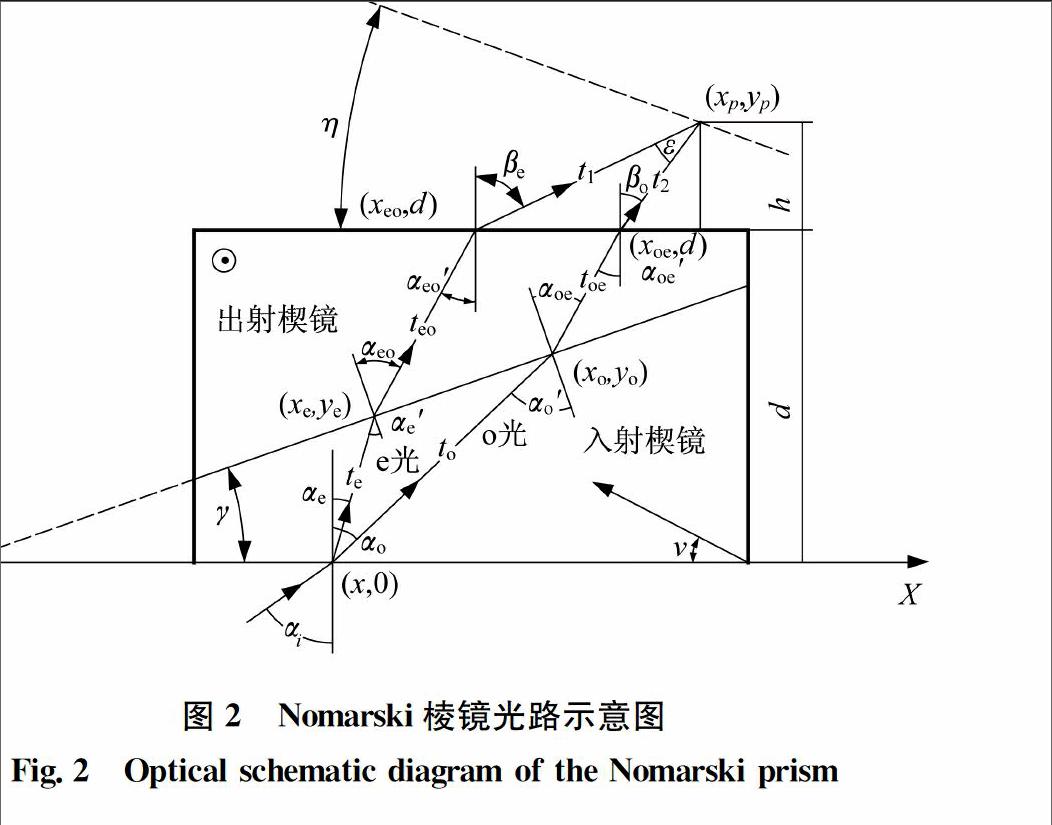
(2)从样品表面反射进入物镜与Nomarski棱镜后的两束光波在纵向上产生一个合适的光程差,以便样品纵向厚度也以光强衬度表现出来,呈现阴暗效果。(3)Nomarski棱镜的相干平面必须与物镜后焦平面重合。2Nomarski棱镜主要设计参数及其计算根据落射式微分干涉相衬显微镜中Nomarski棱镜相干平面与物镜后焦平面重合,且与入射线偏振光垂直的准则,建立如图2所示的线偏振光在Nomarski棱镜中传播的几何光学图解。图中,胶合棱镜楔角为γ,厚度为d,入射楔镜光轴倾角为ν,偏振光入射角为αi,通过棱镜后形成两束光波的分束角为ε,o光的主折射率为no,e光的主折射率为ne。现对线偏振光进入楔镜胶合镜组后形成的o光与e光进行光路追迹计算:(1)偏振光由空气进入到入射楔镜,假设入射点的坐标为(x,0),根据Snell 定律,可得到o光的波法线折射角αo为no·sinαo=n·sinαi(1)式中空气介质的折射率n为1。
(5)线偏振光由空气介质进入到入射楔镜,其振动方向与入射楔镜光轴方向处于同一平面时,即e光的主平面与入射面重合,根据文献[3]可建立图3所示的e光波法线与光线的关系示意图。图中波法线与光轴的夹角为θ,波法线折射角为αk,光线与波法线的夹角为α,即离散角,光线的折射角为αe,可通过先求出波法线方向的折射率与折射角,再求出光线的折射角,最后确定光线在棱镜中的传播方向。
干涉显微镜的Nomarski棱镜通常设置在平行光路中,通过改变偏振光线的入射点坐标,可得到出射光束交点(xp,yp)轨迹,而通过棱镜后形成的分束光程差Δ不随入射点的坐标变化而改变,由式(29)可知出射光束的位相差稳定,即聚焦于该平面上的偏振光束通过检偏镜后,满足发生干涉的条件,通过坐标取值可以求得相干平面倾角η。3Nomarski棱镜主要设计参数优化分析落射式微分干涉相衬显微镜的Nomarski棱镜组件一般设置在物镜与观察头座之间,常采用无限远成像光学系统,因此棱镜相干平面距离h设计在30~35 mm之间比较适宜于结构设计与装调。同时考虑入射照明光束与相干平面垂直,需将棱镜组倾斜安装在成像光学系统中,因此照明光束的入射角不宜过大或过小,入射角αi一般设计在10°以内。
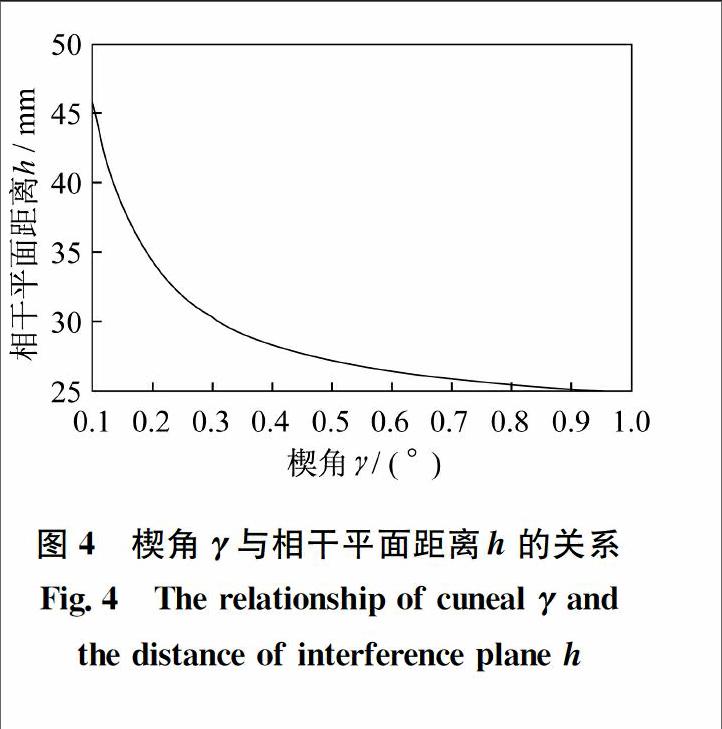
3.1棱镜楔角γ与相干平面距离h间的关系取棱镜材料为石英晶体,假设光轴倾角ν=-9.5°,偏振光入射角αi=-4.5°,晶体厚度d=2.5 mm,入射点坐标x=325 mm。以楔角γ和相干平面距离h作为变量,得到关系曲线如图4所示。从曲线图可以看出,相干平面距离h随楔角γ的增加单调递减。当γ∈[0.1°,0.2°]区间递减时,相干平面距离h随楔角的变化显著,而当γ≥0.8°时,相干平面距离随楔角变化越来越少。根据相干平面与物镜后焦平面重合特性,以及结构尺寸来确定合理的相干平面距离,从而选取合适的楔角γ。
3.2晶体光轴倾角ν与相干平面距离h间的关系取楔角γ为0.2°,将光轴倾角ν与相干平面距离h设置为变量,其余参数与讨论γh关系相同,利用MATLAB程序得到光轴倾角ν与相干平面距离h的关系曲线如图5所示。从曲线图可知,ν与h呈近似余弦变化。当ν∈[-90°,0°]时,h为正值;当ν=-55°左右时h有最大值;而ν∈[0°,90°]时,h为负值,即相干平面进入到棱镜里面,且在ν=55°左右时h有最小值,这时就相当于一个Wollaston棱镜。在高倍物镜中,后焦面往往是在物镜里面,因此从系统整体结构要求来说,Wollaston棱镜是不可能符合落射式微分干涉相衬显微镜的设计要求。
3.3偏振光入射角αi与相干平面距离h间的关系在不改变其他参数的情况下,假设光轴倾角ν=-9.5°,在MATLAB程序中将入射角αi及相干平面距离h设为变量,可得到关系曲线如图6所示。从图中可以看出,h的正负与αi的大小无关,只影响h值的大小,相干平面距离正负性是由光轴倾角ν决定,入射角αi的取值范围在±10°以内能取得良好的相干平面距离。
3.4晶体光轴倾角ν与分束角ε的关系取楔角γ=0.2°,入射角αi=-4.5°,晶体厚度d=2.5 mm,入射点坐标x=325 mm,将光轴倾角ν设置为变量,取值范围为0°~180°,通过MATLAB程序可得到ν与出射光线夹角βo、βe的曲线关系如图7所示,由图可知出射角βo不随光轴倾角的变化而改变,出射角βe则随光轴倾角呈函数变化。当ν=-90°时,出射角βe=-4.5°,即入射角αi=βe=-4.5°。当ν=0°、-180°时出射角βe有最大值,因为分束角ε=βe-βo,此时分束角具有最大值,也证明了当楔角为一确定值时,Wollaston棱镜具有最大分束角。根据分束角与出射光束角βo、βe的关系,通过MATLAB程序可得到光轴倾角ν与分束角ε的关系曲线如图8所示。分束角ε直接决定出射光束横向剪切量的大小,且横向剪切量应小于或等于物镜的最小分辨率。显微物镜的分辨率可由下式求得[9]:σ=0.61λNA(30)式中NA为显微物镜的数值孔径。
由式(30)求得显微物镜最小分辨率,再根据物镜的焦距可以确定棱镜分束角ε,由于分束角非常小,可以近似于ε≤σ×180f×π(31)式中f为物镜焦距。
3.5偏振光入射角αi与相干平面倾角η间的关系在微分干涉相衬显微成像系统中,Nomarski棱镜干涉场是倾斜的,所以必须转动棱镜改变入射角αi,使干涉场与系统光轴相互垂直,由图2可知,当αi与η大小相等、方向相反时,可满足干涉场与系统光轴相互垂直的条件,在MATLAB程序中,将αi与η作为变量,其余参数不变,可得到两者间关系曲线如图9所示,从曲线图可以看出相干平面倾角η随入射角αi呈波动变化,而入射角αi在±10°以内可以取得符合条件的倾角η值。4实例应用分析与设计现以10倍无限远平场消色差物镜为例,优化设计与之相匹配的Nomarski棱镜。设偏振光束主波长λd=587.56 nm,物镜主要技术参数:数值孔径NA=0.25,焦距f=-20 mm,物镜后焦平面距离L=-8.2 mm。Nomarski棱镜组通过一块金属拉板安装在物镜转换器座内,Nomarski棱镜组安装结构示意如图10所示,图示中h为棱镜相干平面距离,从系统结构分析,h值要求在35 mm左右比较理想。
由图4和图5可知,当楔角γ∈[0.1°,0.3°],光轴倾角ν∈[-20°,0°]时,相干平面距离h可能符合设计要求。当γ值较小时,相干倾角η随楔角γ变化不大而基本上由光轴倾角ν决定[10],在MATLAB程序中将光轴倾角ν设为变量,假设楔角γ=0.1°,厚度d=2.0,得到αi、η与ν值见表1。在MATLAB程序中,将楔角γ与厚度d作为变量,以表1中的入射角αi对应的倾角ν作为设计取值,求取符合相干平面距离h与分束角要求的几组棱镜主要结构参数值,见表2。根据分束角ε≤0.004 1°,同时考虑棱镜制造工艺,要求楔角与厚度值大一些,因此本设计实例选择入射角αi=-4.05°,光轴倾角ν=-8.889°,棱镜楔角γ=0.20°,棱镜厚度d=3.333 mm,得到棱镜相干平面处于棱镜外部,与棱镜出射表面相距34.90 mm,分束角ε=0.003 571°,小于显微物镜分辨率角0.004 1°。光程差Δ=0.009 6 mm,即通过棱镜的偏振光束产生的纵向剪切量接近于显微物镜1倍焦深值。5结论在Nomarski棱镜优化设计过程中,要综合考虑显微镜系统结构与光学制造工艺,优先确立相干平面距离h、棱镜厚度d以及入射角度αi的取值范围,这样有利于运用MATLAB程序对棱镜主要结构参数之间的关系进行优化分析,可得到更加直观的关系变化曲线,使复杂的数据计算转变为系统结构与工艺性能分析,得到的设计结果更具有应用价值。参考文献:
[1]杨险峰,叶梅,叶虎年.Nomarski偏光棱镜设计[J].光学仪器,2002,24(6):3034.
[2]陈峻堂.微分干涉相衬显微术[J].光学仪器,1984,6(1):115.
[3]徐福候.诺马斯基棱镜的原理及其计算方法[J].光学仪器,1983,5(2):1319.
[4]汪相.晶体光学[M].江苏:南京大学出版社,2009:67.
[5]李家泽,朱保亮,魏光辉.晶体光学[M].北京:北京理工大学出版社,1989:256278.
[6]PLUTA M.Nomarskis DIC microscopy:a review[J].SPIE,1994,1846:1024.
[7]李景镇.光学手册[M].西安:陕西科学技术出版社,1986:498502.
[8]王之江.实用光学技术手册[M].北京:机械工业出版社,2007:791793.
[9]迟泽英,陈文建.应用光学与光学设计基础[M].南京:东南大学出版社,2008:335337.
[10]WILK J.Localization of the point of beam shearing in birefringent prisms[J].Optyka,1976,11:187192.
(编辑:刘铁英)
