基于ANP与模糊TOPSIS的城市地下物流系统集装单元选择决策方法

马成林，杨学春，董景峰，马 超，安立华

（1.东北林业大学，黑龙江 哈尔滨 150040；2.合肥学院，安徽 合肥 230601）

基于ANP与模糊TOPSIS的城市地下物流系统集装单元选择决策方法

马成林1，杨学春2，董景峰1，马 超1，安立华1

（1.东北林业大学，黑龙江 哈尔滨 150040；2.合肥学院，安徽 合肥 230601）

目前城市地下物流系统多采用托盘作为集装单元，但其规格繁多需要从中选择，基于此提出了多准则托盘选择决策方法。首先，确定托盘选择评价指标并进行量化，进而分析评价指标之间的制约关系，建立ANP评价指标关系结构模型并确定评价指标权重，从而构建模糊评价模型并设计模糊TOPSIS求解算法，求得托盘尺寸。最后，给出了一般内陆城市地下物流系统托盘选择算例。结果表明：该方法可以确定城市地下物流系统托盘尺寸，统一系统基础单元规格，其中一般内陆城市地下物流系统托盘选择尺寸宜为1 200×1 000mm。

地下物流系统；集装单元；ANP；模糊TOPSIS

1 引言

建设城市地下物流系统首先就要解决地下物流系统集装单元标准化问题，同时城市地下物流系统功能要求地下物流系统集装单元的标准化程度必须很高。钱七虎，郭东军（2007）；马祖军（2004）认为集装单元对地下物流系统运输效率、货运周转、管道直径等很多因素都有影响，比如集装单元越大，通道直径越大，建设成本越高，单位时间运输的货物越多，收益越大，这种背反关系需要合理的权衡[1-2]。目前，各国地下物流系统的托盘尺寸不一（见表1），我国托盘标准和使用的种类又很多（见表2），需要从6种托盘中选择一种作为城市地下物流系统的集装单元。

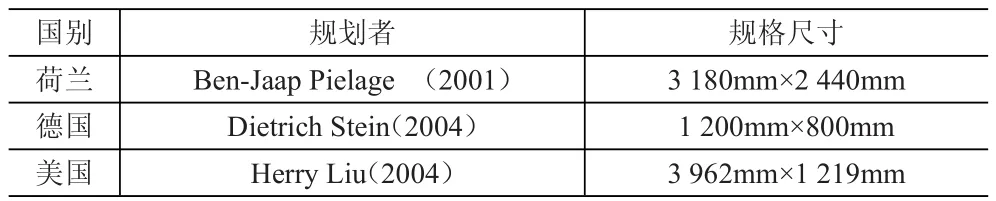
表1 地下物流系统托盘主要规格[3-6]

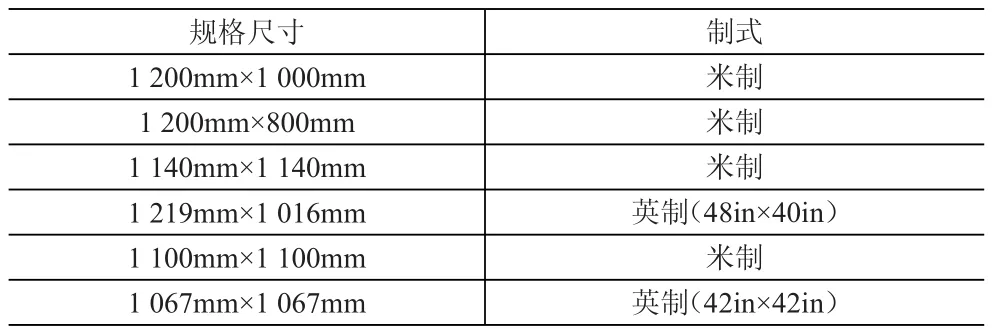
表2 托盘的类别与尺寸[7-8]

由于托盘选择的影响因素较多，宜采用多准则决策方法进行解决[9]。在以往的托盘选择过程中，决策者或规划者往往从单一因素进行决策，如李太平分别从货运列车载货效率[10]、商品出口市场[11]、托盘标准应用现状[12]、托盘载货效率[13]、选用国际标准数量[14]和增进商品出口[11]角度论述了托盘标准的选择，缺少多属性综合性托盘选择研究。另外，关于城市地下物流系统托盘选择的研究尚处于“真空期”，已建或者尚在研究的城市地下物流系统往往针对单一运输方式或者单一行业进行托盘选择，如荷兰OLS-ASH系统用来衔接Schiphol机场与Aalsmeer花卉市场之间的货运，其托盘选择了10英尺飞机托盘3 180mm×2 440mm，其选择过程缺乏对公路运输、城市配送、仓储等问题的考虑。

2 托盘选择决策思路

城市地下物流系统的托盘选择决策模型思路如图1所示。首先，构建托盘选择准则并进行比较分析，构建准则间的关系矩阵，利用ANP法得到准则直接关系矩阵，再利用DEMATEL法得到最终关系结构矩阵；其次，应用ANP法进行指标的计算，得到各个指标的模糊评价权重值；最后应用模糊TOPSIS法进行托盘的评价指标排序，找到地下物流系统的最佳托盘尺寸。

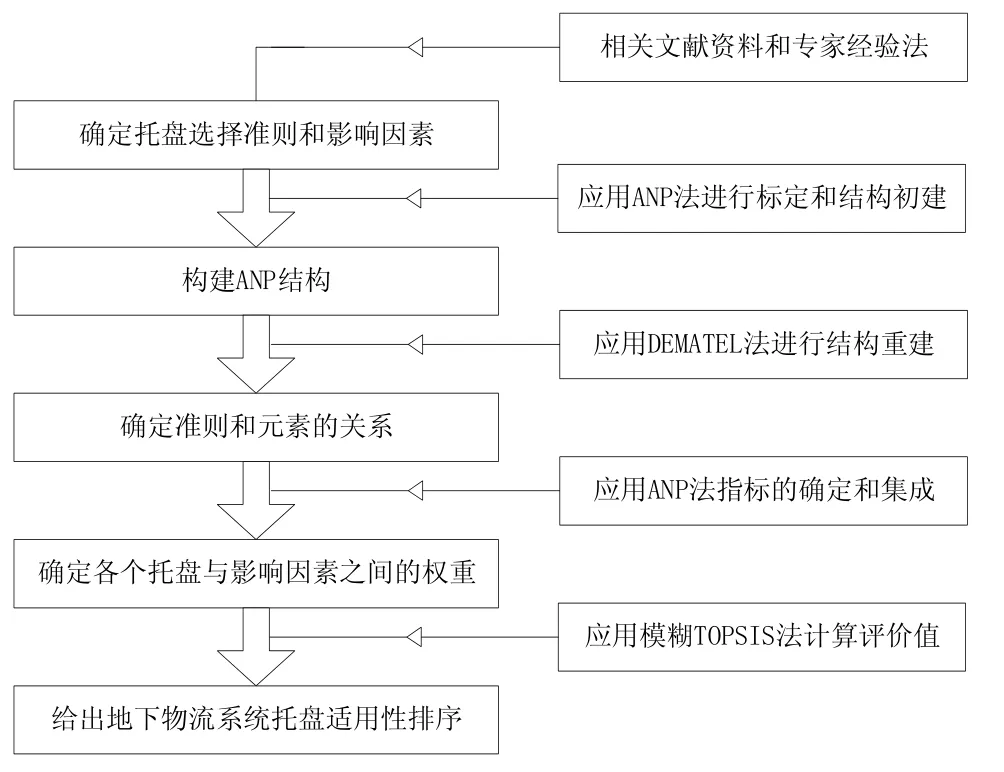
图1 地下物流系统托盘选择思路图

3 评价指标

城市地下物流系统的托盘选择要从多个方面去衡量和评价，不能仅仅局限于托盘自身的特性，也不能单一地从城市地下物流系统发展的角度，要立足于整个城市物流的发展，着眼于城市当前发展情况和未来发展趋势，多层次、多角度地分析城市地下物流系统托盘选择的相关影响因素，从托盘选择导致的后果和影响托盘选择的因素两个方面建立评价指标体系，见表3。

表3 城市地下物流系统托盘选择指标

4 托盘选择的模型与步骤

步骤1：建立托盘选择影响关系的ANP结构。建立主因子有向图。通过定位分析确定城市地下物流系统托盘选择的主因子P（P1，P2，…，Pm），次因子p（p11，p12，…，p1n，p21，p22，…，p2l，…，pm1，pm2，…，pmk），其中Pm为备选托盘元素组。初步构架ANP结构和准则之间的相互影响有向图。建立直接关系矩阵。根据ANP初步结构，构建P1，P2，…，Pm之间的直接影响矩阵Z，并将直接矩阵Z转化为标准矩阵Y[18-19]。

其中zij表示在主因子Pi对主因子Pj的影响程度。

其中：

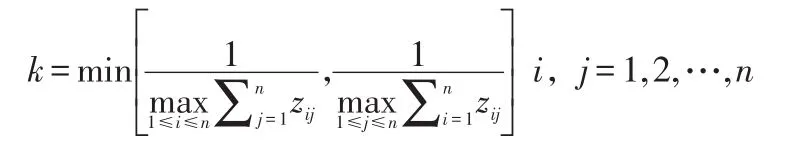
步骤2：计算最终关系矩阵，构建ANP主因子结构图。建立总影响矩阵T，经式（3）转化得到Ti，i=0，1，2，…，m。根据影响因素间实际关系，选取临界值p，经式（4）转化得到最终关系矩阵G，进而重新构建ANP准则间结构。

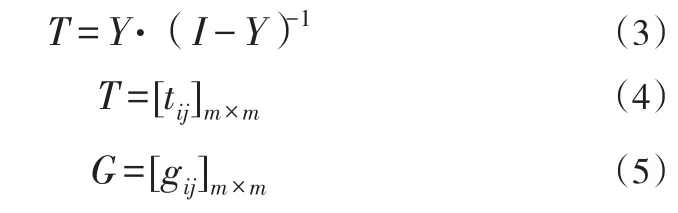
其中：

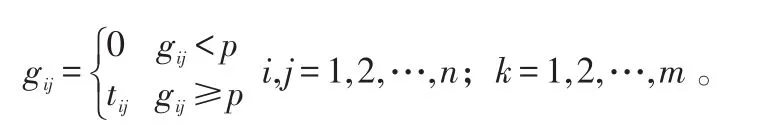
根据ANP主因子间新结构，构建 Pk主因子下pk1,pk2,…,pkn，k∈{1，2,…，m} 之间的直接关系矩阵，从而得到完整ANP结构。

步骤3：确定托盘选择评价指标权重。建立ANP判断矩阵。构建决策者 t（t=1,2,…,n）的判断矩阵。主因子P1,P2,…,Pm对主因子Pj判断矩阵为At（jl）和主因子Pi的元素p,p,…,p对主因子P元素 p影响的判断矩阵为（jl）[18-19]。

i1i2injjl

5 算例分析

选取我国一般内陆城市作为研究对象，进行地下物流系统托盘选择决策计算。按照步骤1、2，建立P1，P2，…，P7之间的直接影响矩阵Z0，如等式（15），其结构如图2所示，根据式（2）-（5）得到ANP总影响矩阵T，如等式（16），选取临界值p=0.111 8，ANP完整关系矩阵G如等式（17），其结构如图3所示。基于SuperDecision和ANP建模方法，建立计算模型（如图3所示）并求得超矩阵（如图4所示），整理后的超矩阵Wt如图5和表4。按照步骤3、4求得超矩阵加权矩阵W__t和加权矩阵Dt，见表5、表6；按照步骤5求得模糊评价矩阵R，见表7。按照步骤6和7，最终得到 p71,p72,…,p76的贴近度C=[0.526 8，0.492 0，0.438 2，0.372 2，0.289 4，0.305 5]，结果托盘1 200mm×1 000mm应作为我国一般内陆城市地下物流系统集装单元。

图2 地下物流系统托盘选择的ANP初始结构图

表4 超矩阵Wt

6 结论

图3 地下物流系统托盘选择的ANP完整结构图

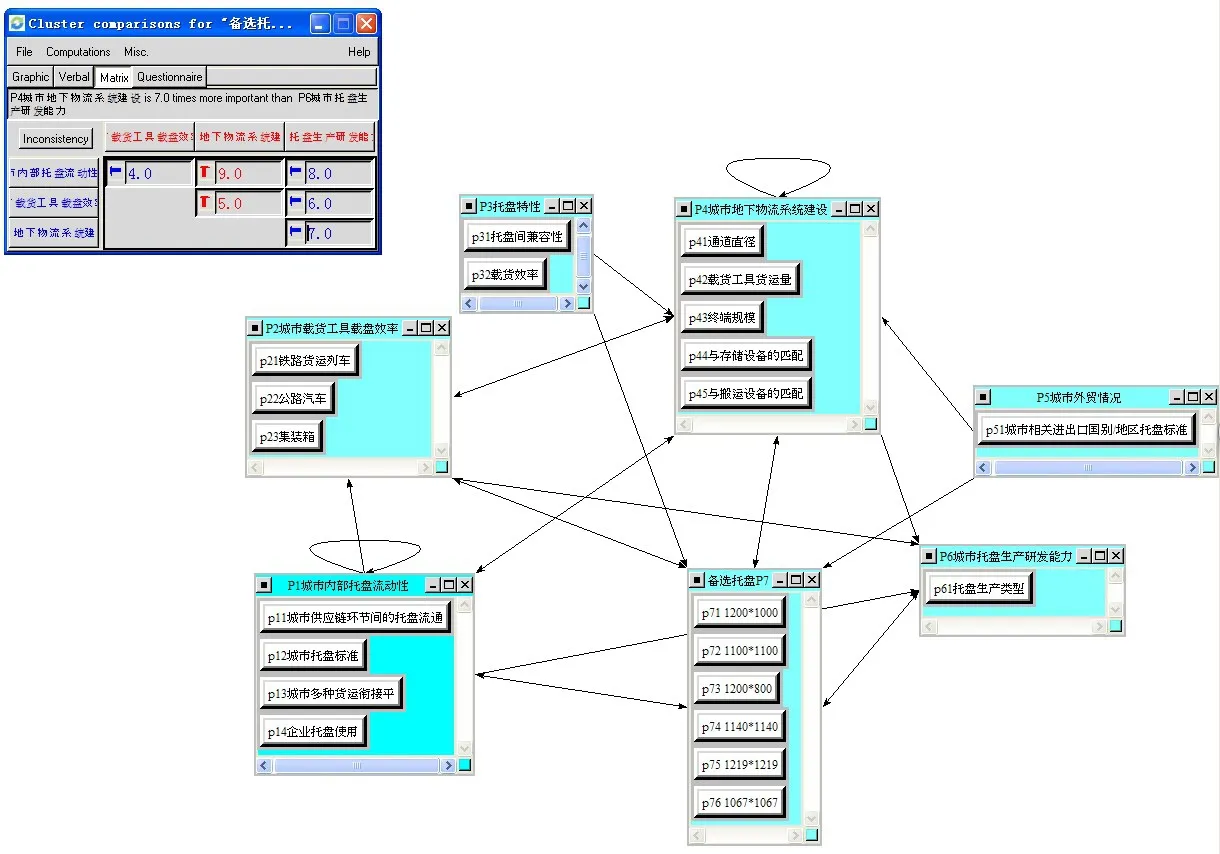
图4 基于SuperDecision的ANP模型和部分关系矩阵

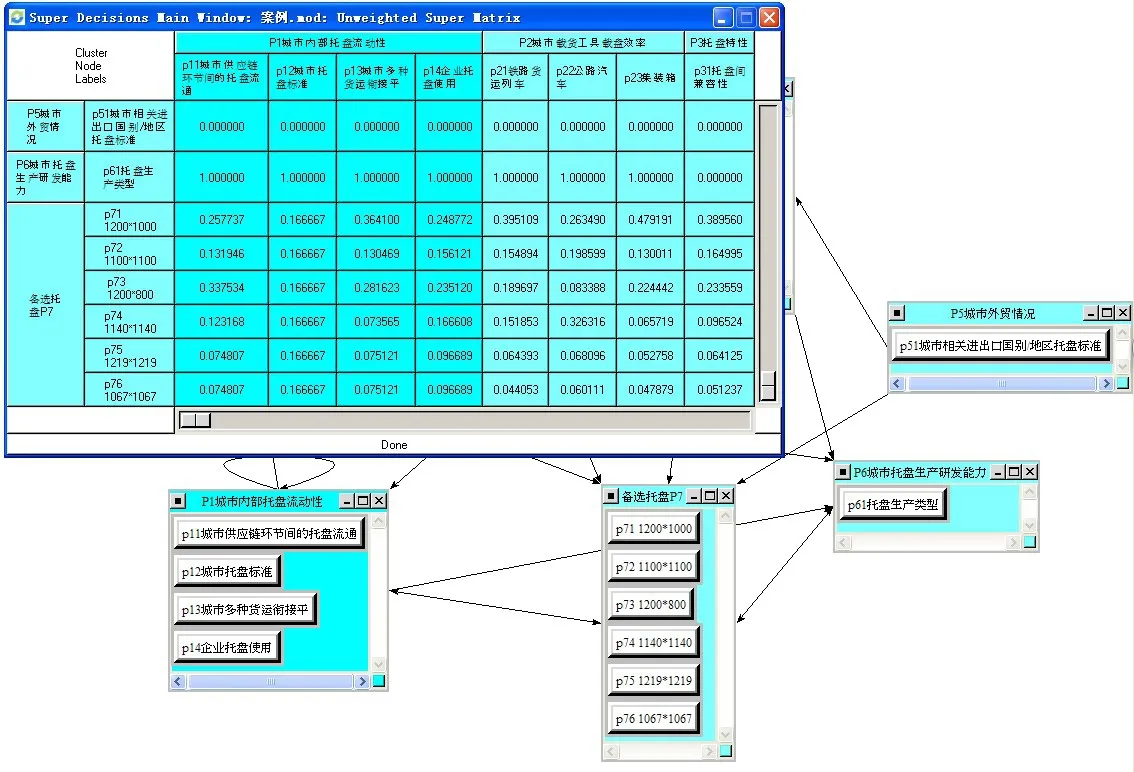
图5 基于SuperDecision求得超矩阵Wt的示意图

本文研究了托盘作为地下物流系统集装单元的选择问题，提出了基于ANP和模糊TOPSIS的地下物流系统托盘选择决策方法，给出了托盘选择决策模型和求解算法，并对一般内陆城市地下物流系统的托盘选择进行了算例研究，结果表明一般内陆城市地下物流系统的托盘规格应为1 200mm× 1 000mm，从而也验证了方法的有效性，为地下物流系统规划研究提供了理论基础。

表5 加权超矩阵

表5 加权超矩阵

p71 p72 p73 p74 p75 p76 p11 0.11 0.06 0.15 0.05 0.03 0.03 p12 0.03 0.03 0.03 0.03 0.03 0.03 p13 0.16 0.06 0.12 0.03 0.03 0.03 p14 0.05 0.03 0.05 0.03 0.02 0.02 p21 0.26 0.10 0.12 0.10 0.04 0.03 p61 0.17 0.17 0.17 0.17 0.17 0.17 p22 0.17 0.13 0.05 0.21 0.04 0.04 p23 0.31 0.09 0.15 0.04 0.03 0.03 p31 0.31 0.13 0.19 0.08 0.05 0.04 p32 0.19 0.07 0.04 0.13 0.33 0.04 p41 0.09 0.07 0.21 0.04 0.03 0.03 p42 0.05 0.09 0.03 0.17 0.29 0.03 p43 0.24 0.07 0.22 0.06 0.04 0.04 p44 0.03 0.10 0.03 0.10 0.10 0.10 p45 0.05 0.10 0.05 0.10 0.10 0.10 p51 0.33 0.12 0.28 0.05 0.04 0.04

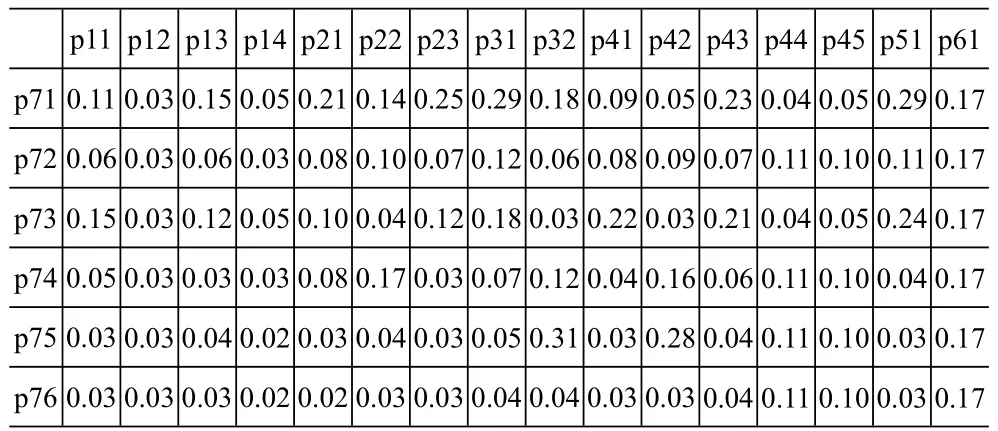
表6 加权超矩阵Dt

表7 模糊评价矩阵R

[1]钱七虎,郭东军.城市地下物流系统导论[M].北京:人民交通出版社, 2007.

[2]马祖军.城市地下物流系统及其设计[J].物流技术,2004,(10):12-15.

[3]Henry L.Feasibility of Using Pneumatic Capsule Pipelines in New York City for Underground Freight Transport[A].Proceedings of the ASCE Pipeline Division Specialty Congress-Pipeline Engineering and Construction[C].2004.

[4]Henry L,Ramesh L,Gandhi M,Robert C,et al.Freight pipelines:current status and anticipated future use[J].Journal of Transportation Engineering,1998,124(4):300-310.

[5]Dietrich S,Robert S,Dietmar B,et al.CargoCap:Feasibility Study of TransportingContainersThrough Underground Pipelines[A].ISUFT 2005 Proceedings[C].2005.

[6]Pielage B-J.Underground Freight Transportation.A New Development for Automated Freight Transportation Systems in the Netherlands[A].2001 IEEE Intelligent Transportation Systems Proceedings,Oakland[C].2001.

[7]吴清一.集装单元化概论[J].物流技术与应用,2007,(1):59-64

[8]吴清一.再论我国托盘共用系统的建立[J].物流技术与应用,2004,(1): 14-19.

[9]徐玖平,吴巍.多属性决策的理论与方法[M].北京:清华大学出版社, 2006.

[10]李太平.论我国物流托盘标准的选择—基于货运列车载盘效率角度[J].物流技术,2007,(3):28-31.

[11]李太平.论我国物流托盘标准的选择—基于增进商品出口角度[J].生产力研究,2006,(8):201-203.

[12]李太平.论我国物流托盘标准的选择—基于托盘标准应用现状角度[J].国际标准化,2005,(12):7-10.

[13]李太平.论我国物流托盘标准的选择—基于托盘载货效率角度[J].企业标准化,2007,(12):28-31.

[14]李太平.论我国物流托盘标准的选择—基于选用国际标准数量角度[J].中国标准化,2006,(4):29-32.

[15]李太平,应瑞瑶.基于启发式算法的物流托盘载货效率研究[J].武汉理工大学学报,2009,33(1):79-82.

[16]汤普金斯,等,著,伊俊敏,袁海波,译.设施规划[M].北京:机械工业出版社,2007.

[17]吴清一,唐英.解读托盘新国标[J].物流技术与应用,2008,(5):82-85.

[18]Ma C L,Mao H J,Li X H,Zhang Y.Study on the reliability measure to select suppliers[A].ICCLTP2008[C].2008.

[19]马成林.我国大城市地下物流系统关键技术研究[D].南京:东南大学,2011.

Study on Decision-making in Selecting Container Units for Urban Underground Logistics Systems Based on ANP and Fuzzy TOPSIS

Ma Chenglin1,Yang Xuechun2,Dong Jingfeng1,Ma Chao1,An Lihua1
(1.Northeast University of Forestry,Harbin 150040;2.Hefei University,Hefei 230601,China)

In this paper,we identified the evaluation indexes in the selection of pallets,then analyzed the restrictive relations among the indexes,built the corresponding ANP structural model,determined the weight of the evaluation indexes and built the fuzzy evaluation model as well as the TOPSIS algorithm for its solution.At the end,we presented a numerical example of pallet selection for the underground logistics system of a generic inland city and determined the suitable pallet size and specification for the city.

underground logistics system;container unit;ANP;fuzzy TOPSIS

F570；F252

A

1005-152X(2015)10-0110-05

2015-09-06

中央高校基本科研业务费专项资金资助项目（DL12BB07）；黑龙江省教育厅科学技术研究项目（12533018）；黑龙江省博士后资助项目（LBH-Z2018）

马成林(1982-)，男，黑龙江人，东北林业大学工程技术学院物流工程系讲师，研究方向：城市地下物流系统、行业物流耦合系统。

10.3969/j.issn.1005-152X.2015.10.031