有限交换环上的广义单位Cayley图的进一步研究

熊腾飞，简国明（.韶关学院 信息科学与工程学院；.韶关学院 数学与统计学院，广东韶关5005）

有限交换环上的广义单位Cayley图的进一步研究

熊腾飞1，简国明2
（1.韶关学院 信息科学与工程学院；2.韶关学院 数学与统计学院，广东韶关512005）

摘要：设R是一个含有非零单位元的有限交换环,U(R)是R的单位群,G是U(R)的一个乘法子群,S是G的一个非空子集并且S-1={s-1|s∈S}⊆S.在研究广义单位Cayley图Γ(R,G,S)的若干性质的基础上，对当S={s}时,Γ(R,U(R), S)的性质作进一步研究，考察Γ(R,U(R),S)的同构问题，得出Γ(R,U(R),S)的团数和顶点着色数,确定Γ(R,U(R),S)是完美图的条件.

关键词：单位Cayley图;团数；顶点着色数;完美图

单位Cayley图是近年来的一个热门研究领域,它们内涵丰富,很好地把图论和代数系统的研究结合起来,提供了研究代数问题的一种新方法.

设n＞1是一个正整数,Zn即模n剩余类环,许多学者对Zn上的单位Cayley图进行了研究,其中文献［1-2］得到了许多很好的结论.2009年,R.Akhtar,M.Boggess等学者提出了一般的有限交换环上单位的Cayley图GR的定义:设R是一个含有非零单位元的有限交换环,U(R)为R的单位群,GR的顶点集是R,顶点x和y相邻当且仅当x-y∈U(R).讨论了GR的直径、围长、自同构群、点连通度、边连通度、团数、着色数、边着色数,而且还解决了GR的平面性和完美性等问题［3］.在此之后,许多专家对环上的单位Cayley图的性质产生了浓厚的兴趣,文献［4-5］得出的一系列成果,使得该领域的成果丰富起来.

在N.Ashrafi等学者提出了一般环上的单位图的概念以后［6］,K.Khashyarmanesh和M.R.Khorsandi推广了单位Cayley图的概念［7］:设R是一个含有非零单位元的有限交换环,U(R)是R的单位群,G是U(R)的一个乘法子群,S是G的一个非空子集并且S-1={s-1|s∈S}⊆S,定义广义单位Cayley图Γ(R,G,S)的顶点集为R,顶点x与y相邻当且仅当存在s∈S,使得x+sy∈G.当G=U(R)时,Γ(R,G,{-1})即单位Cayley图,而Γ(R, G,{-1})就是单位图.文献［3，6-7］的一些结论推广到Γ(R,G,S)中,很好地把环上的单位Cayley图和单位图统一了起来,范围更加宽广,内涵更加丰富.

本文所指的图都是简单图,即没有自环和重边的图.设G是一个图,V(G)表示图G的顶点集;设a,b∈V(G), 若a,b是一条边的两个端点,则称a与b是相邻的.独立集指的是图中两两不相邻的顶点所组成的集合.图G称为二部图,如果V(G),是两个互不相交的独立集的并集,这两个独立集称为图G的部集.

文献［1］确定了当S={s}时,广义单位Cayley图Γ(R,G,S)的正则性,Γ(R,U(R),S)中任意两点的公共邻接点个数以及边着色数.本文主要对Γ(R,U(R),S)的性质作进一步研究,考察当S={s}时,Γ(R,U(R),{1})与Γ(R,U (R),{-1})的同构问题,计算Γ(R,U(R),S)的团数和顶点着色数，确定Γ(R,U(R),S)是完美图的条件.

1　定义及引理

定义1称一个图是完美的,如果它的任意一个诱导子图H,都有χ(H)=ω(H),其中χ(H)和ω(H)分别表示H的顶点着色数和团数［8］.

定义2图G中长度不小于5并且是奇数的诱导圈称为奇洞［2］.

引理1设R是一个含单位元的交换环.若R是Artin环,则R可以表示成有限个Artin局部环的直和:( Ri为Artin局部环).如果又有(Ri为Artin局部环),则t=t,并且有{1,2,…,t}的一个置换σ,使得

引理2设R是一个有限环,则1+1∈U(R)当且仅当|R|是奇数.

引理3设R是一个含非零单位元的交换环,J(R)是R的Jacobson根,G(R)表示环R上的单位图.若x,y∈R,则：

（1）若x+J(R)和y+J(R)在图G(R/J(R))中相邻,则x+J(R)中的每一个元都与y+J(R)的任何一个元在G(R)中相邻;

（2）若(1+1)·x∈U(R),则x+J(R)是G(R)中的一个团［6］.

引理4设R是一个含单位元的交换环,M是R的一个极大理想且|R/M|=2,则图Γ(R,U(R),S)是一个二部图［7］.

引理5设R是一个含非零单位元的有限交换环,J(R)是R的Jacobson根.若S={s},1+s∈J(R),则Γ (R,U(R),S)≅Γ(R,U(R),(-1)).

证由引理1,设是局部环,其极大理想为Mi,i=1,2,…,t.设s=(s1,s2,…,st),则1+s=(11+s1, 12+s2,…,1t+st),1i为Ri的单位元,i=1,2,…,t.x=(x1,x2,…,xt),y=(y1,y2,…,yt)是R的两个不同的元.

若x和y在Γ(R,U(R),{-1})中相邻,则对于i=1,2,…,t,都有xi-yi∈U(Ri),故xi+siyi∈U(Ri),所以x+sy∈U (R),即x和y在Γ(R,U(R),{s})中相邻;反过来,若x和y在Γ(R,U(R),{-1})中不相邻,则存在i∈{1,2,…,t},使得xi-yi∈Mi,所以xi+siyi∈Mi,故x+sy∉U(R),即x和y在Γ(R,U(R),{s})中不相邻.综上所述,若1+s∈J(R), 则Γ(R,U(R),{s})≅Γ(R,U(R),{-1}).

引理7图G是完美的当且仅当G和G的补图G没有奇洞［2］.

2　主要结果及证明

文献［7］证明了,当R是偶数阶局部环时,Γ(R,U(R),{1}和Γ(R,U(R),{-1}是同构的,然而,当R是偶数阶非局部环,且1+1∉J(R)时,Γ(R,U(R),{1})和Γ(R,U(R),{-1})也有可能是同构的.

定理1若n=2αpβ,α,β≥1,p是素数且p＞2,则Γ(Z,nZ,U(Z/nZ),{1})≅Γ(Z,nZ,U(Z/nZ),{-1}).

证设＜2＞为2在Z/nZ中生成的理想,则Γ(Z,nZ,U(Z/nZ),{-1})和Γ(Z,nZ,U(Z/nZ),{1})都是一个以陪集＜2＞和1+＜2＞为部集的二部图.定义映射使得,显然f是一个双射.下面分三种情况讨论:

（1）若x,y∈Z/nZ恰有一个是单位,不妨设x∈U(Z/nZ),则f(y)=y.一方面,若x-y∈U(Z/nZ),则f(x)+f(y)=-x+y=-(x-y)∈(Z/nZ);另一方面,若x+y∈U(Z/nZ),因为存在-x∈U(R),使得f(-x)=x,所以-x-y=-(x+y)∈U (Z/nZ).因此,x-y∈U(Z/nZ)当且仅当f(x)+f(y)∈U(Z/nZ).

（2）若x,y∈U(Z/nZ)⊆1+＜2＞,则x-y∉U(Z/nZ)并且x+y∉U(Z/nZ).

（3）若x,y∉U(Z/nZ),当x-y∈U(Z/nZ)时,不妨设x∈＜2＞,y∈1+＜2＞.因为y∉U(Z/nZ),所以y必为零因子,因此y=mp∈＜p＞,m是一个整数.又因为(x+y)-(x-y)=2y=2mp,因此(x+y)-(x-y)∈＜2＞∩＜p＞.令(x+y)-(xy)=z,注意到Z/nZ只有＜2＞和＜p＞两个素理想,故x+y=z+(x-y)∈U(Z/nZ).同理可证,若x+y∈U(Z/nZ),就有xy∈U(Z/nZ).

综上所述,x与y在Γ(Z,nZ,U(Z/nZ),{-1})中相邻当且仅当f(x)与f(y)在Γ(Z,nZ,U(Z/nZ),{1}中相邻,故Γ(Z, nZ,U(Z/nZ),{1}≅Γ(Z,nZ,U(Z/nZ),{-1}.证毕

设R是一个含非零单位元的有限交换环.当R是一个局部环时,Γ(R,U(R),{-1})是一个完全|R/M|部图, M是R的极大理想,其团数和顶点着色数均为|R/M|.取S={s},下面考察当1+s∈U(R)时,Γ(R,U(R),S)的团数ω(Γ(R,U(R),S))和顶点着色数χ(Γ(R,U(R),S)).

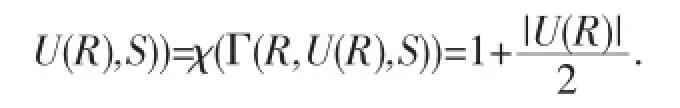
证令u=1+s∈U(R),则su=s(1+s),因为s·s=1,所以又有su=1+s,即su=u,故s=1,这样就有Γ(R,U(R), S)=Γ(R,U(R),{1}).由引理2知|R|是奇数,因为|U(R)|=|R|-|M|,所以是偶数.

接下来证明χ(Γ(R,U(R),S))≤1+|U(R)|.考虑到{0}∪{x∈|∈A}是一个具有1+|U(R)|个顶点的团,用1+ 22给这个团着色.因为M是图Γ(R,U(R),S)的一个独立集,所以可用0的颜色给M的所有点着色.对于A的每一个元,因为,所以中所包含的任意一点与-r中所包含的任意一点在Γ(R,U(R),S)中不相邻,因此可用中已有的|M|种颜色为-r中的所有点着色.因此.注意到.证毕.

(1)f1=2;

(2)1+s∈J(R),且t≤2.

证若f1=2,设M=M1⊕R2⊕…⊕Rt,易知M是R的一个极大理想,且|R/M|=2.由引理4,Γ(R,U(R),S)是一个二部图,所以Γ(R,U(R),S)是一个完美图.

若1+s∈J(R),t≤2,由引理5知Γ(R,U(R),S)≅Γ(R,U(R),S),{-1},再由引理6 Γ(R,U(R),S)是一个完美图.

接下来,考虑当f1≥3时的情形:

(a)若1+s∈J(R)且t≥3,由引理6 Γ(R,U(R),S)不是完美图.

(b)若1+s∉J(R),则t≥2.I={i∈{1,2,…,t}|1i+si∈Mi},易知I和J都是非空集合.取Γ(R,U(R),S)的5个点, a,b,c,d,e,使得:a=(01,02,…,0t);b=(b1,b2,…,bt),若i∈I,则bi=1,否则bi=0;b=(11,12,…,1t);di=(d1,d2,…,dt),若i∈I,则，这里,否则,若以上的0i表示Ri的零元,i∈1,2,…,t.由定理4的证明知,对任意i∈{1,2,…,t}-I,都有si=li,不难看出a,b,c,d,e是Γ(R,U(R),S)的补图的一个长度为5的奇洞,由引理7,Γ(R,U(R),S)不是完美图.命题得证.

参考文献：

［1］熊腾飞,简国明.一类有限交换环上的广义单位Cayley图的若干性质［J］.重庆师范大学学报：自然科学版,2015,32(1):60-63.

［2］Klotz W,Sander T.Some properties of unitary Cayley graphs［J］.Electron J Combin,2007（14）:45.

［3］Akhtar R,Boggess M,Jackson-Henderson T,et al.On the unitary Cayley graph of a finite ring［J］.Electron J Combin,2009 （6）:117.

［4］Kiani D,Aghaei M M H.On the unitary Cayley graph of a ring［J］.Electron J Combin,2012,19(2):10.

［5］Liu X G,Zhou S M.Spectral properties of unitary Cayley graphs of finite commutative rings［J］.Electron J Combin,2012,19(4):13.

［6］Ashrafi N,Maimani H R,Pournaki M R,et al.Unit graphs associated with rings［J］.Comm Algebra,2010（38）:2851-2871.

［7］Khashyarmanesh K,Khorsandi M R.A generalization of the unit and unitary Cayley graphs of a commutative ring［J］.Acta Mathematica Hungarica,2012,137(4):242-253.

［8］West D B.Introduction to Graph theory［M］.2nd ed.New Jersey:Prentice Hall,2000.

［9］冯克勤.交换代数基础［M］.北京:高等教育出版社,1986.2.School of Mathematics and Statistics,Shaoguan University,Shaoguan 512005,Guangdong,China）

（责任编辑：邵晓军）

中图分类号：O157.5

文献标识码：A

文章编号：1007-5348（2015）06-0001-04

［收稿日期］2015-03-26

［作者简介］熊腾飞（1985-），男，广东韶关人，韶关学院信息科学与工程学院教师，硕士；研究方向：环论、代数图论.

Further Study on a Generalization of the Unitary Cayley Graphs of a Finite Commutative Ring

XIONG Teng-fei1,JIAN Guo-ming2
（1.Institute of Information Science and Engineering,Shaoguan University;

Abstract:The paper suggests R be a finite commutative ring with non-zero identity and U(R)be the unit group of R.It also supposes that G is a multiplicative subgroup of U(R),and S is a non-empty subset of G such that S-1= {s-1|s∈S}⊆S.By the structure of a finite commutative ring,［1］have given some properties of a generalization of the unitary Cayley graphs Γ(R,G,S),where S={s}.The paper makes further research on the properties of Γ(R,U(R),S)where S={s},considering the problem of its isomorphism,achieving the clique number and vertex chromatic number of Γ(R,U(R),S).In addition,it decides Γ(R,U(R),S)is a key to perfect graphs.

Key words:unitary Cayley graphs;clique number;vertex chromatic number;perfect graphs