一种排序变异的改进蝙蝠算法
2015-08-01陈梅雯
陈梅雯
(福建农林大学 计算机与信息学院,福建 福州 350002)
一种排序变异的改进蝙蝠算法
陈梅雯
(福建农林大学 计算机与信息学院,福建 福州 350002)
摘要:针对蝙蝠算法易陷入局部最小值等不足,提出一种改进的蝙蝠算法,局部搜索采用指数交叉变异,提高局部搜索能力的同时又保持种群多样性;受自然界启发,优良的品种总是包含有好的信息,采用排序策略选择较优质的个体进行变异来产生优质的候选解。在典型测试函数上对新算法进行了仿真,结果表明改进的蝙蝠算法能够有效提高算法的收敛速度并改善解的质量,与其它改进蝙蝠算法和改进群智能算法的比较表明,改进算法在求解多维函数优化问题上是具有竞争力的。
关键词:蝙蝠算法;变异;多样性;排序
近年来,受自然规律和生物群体智能行为的启发,陆续提出了一些新颖的仿生群智能算法,如鱼群算法、蜂群算法、萤火虫算法、布谷鸟算法(Cuckoo Search,简称CS)等[1],在科学计算和工程技术领域内显示出独特的特点和应用效果。例如布谷鸟算法模拟布谷鸟寄生育雏行为以及鸟类或果蝇的Lévy飞行行为。蝙蝠算法(Bat Algorithm,简称BA)[2]是模拟自然界中蝙蝠通过超声波搜索,回声定位行为,捕食猎物的生物学特性发展而来的一种新颖的群智能优化算法,最早由Yang X S提出。目前BA算法已经广泛应用于自然科学与工程科学领域中,但也存在易陷入局部极小点、后期收敛速度较慢等问题,针对这些不足,目前国内外学者对BA算法提出相关的改进策略,如谢健等[3]提出的基于Lévy飞行轨迹的LBA算法,Wang等[4]把和声搜索作为变异算子嵌入到BA算法中,Iztok等[5]把DE算法策略应用于局部搜索中,以此加强算法的局部求精能力,He等[6]提出的基于模拟退火和高斯扰动的SAGBA算法,这些改进策略都有效提高了BA算法的求解精度和收敛速度。
BA算法中个体的飞行由最佳解引导,以及局部搜索随机游走于最佳解附近,这些导致种群多样性降低过快,易陷入局部极小值,影响了算法的寻优性能;其次,响度参数影响候选解的接收概率,有可能会使好的解丢失。本文受自然界现象的启发,即优良的品种总是包含有好的信息,它们应该有更多的机会被用于引导其它物种。因此,针对BA算法局部搜索的不足,本文提出基于排序变异的改进BA算法(improved bat algorithm with ranking-based mutation,简称RBA)。仿真实验结果说明RBA算法有效地提高了算法的局部求精能力,并改善收敛速度和解的质量。
1 蝙蝠算法
假设在D维空间中,蝙蝠i在t时刻的位置xit、速度vit更新公式为:

其中,β∈[0,1]是来自均匀分布的随机变量,x*是全局最优解。
对于局部搜索部分,当一个解被选为当前最好解时,新解通过如下的随机游走方式产生:

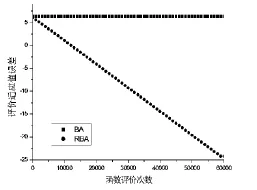
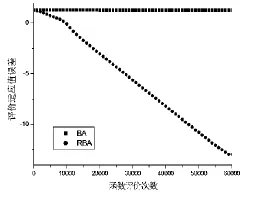
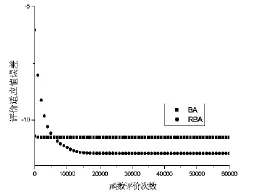
这里的ε∈[-1,1]是一个服从均匀分布的随机数,At= 基于上述,基本的BA算法的基本流程如算法1表示。 算法1.Bat Algorithm Begin 初始化各参数及种群位置xi. 计算适应值,得出fitmin,x*. Whi1e(不满足停止条件) For(i=1 to popsize) 通过公式(1-3)产生新解.{飞行} If(rand>ri) 通过公式(4)产生解. EndIf{局部搜索} 检查是否越界. 计算新的适应值fitnew. If(fitnew 接收新解. 利用公式(5-6)更新ri和Ai. EndIf EndFor 找出当前最佳解fitmin,x*. EndWhi1e End 2.1指数交叉变异 本文的重点是提高局部搜索的求精能力,算法1中的局部搜索受差分算法的启示,公式(4)改为其中r1,r2,r3∈[1,popsize],且r1≠r2≠r3,r∈[-1,1]为服从均匀分布随机数,达到双向搜索,扩大搜索范围。 差分算法中有二项式和指数两种交叉方式,Lin[7]和Zhao[8]的研究表明,使用指数概率分布的交叉效果要好于二项式交叉,因此本文采用指数交叉操作进行局部搜索。具体描述如算法2。 算法2.指数交叉操作 Begin 用公式(7)修改第j维 Whi1e(rand<=Cr&1en<=dimension) j=mod(j,dimension)+1 用公式(7)修改第j维 1en=1en+1; Endwhi1e End 其中Cr为指数分布概率,j∈[1,dimension]中的随机数,1en表示修改维数的长度。 2.2排序选择策略 一般来说,对于公式(7)中的r1,r2,r3是从父代随机选取的。在自然界中,优质的品种总是包含有好的信息,它们应该有更多的机会被用于引导其它物种。因此通过排序的方式,让较优质的个体更有机会被选中,Gong[9]等人的实验表明,基于排序选择的策略用于原始的差分算法和改进的差分算法中,其搜索性能都有明显提高。 (1)排名分配:种群中个体的适应度值按从优到差进行排列,每个个体的排名分配按照如下公式(8): Ri=NP-i,i=1,2,…,NP(8) 其中NP表示种群的大小,Ri表示第i个个体的分配值,从公式(8)可以看出,当前种群中,排名越前的个体获得的分配值就越大。 (2)选择概率:当前种群中每个个体的选择概率按照公式(9): 其中pi表示第i个个体的选择概率,很明显排名越前的个体,其概率值越高。 基于排序策略的选取公式(7)中的r1,r2的具体实现如算法3描述。 算法3.排序策略 Begin 随机选择r1[1,popsize] Whi1e(rand>pr1or r1==i) 随机选择r1[1,popsize] Endwhi1e 随机选择r2[1,popsize] Whi1e(rand>pr2or r2==r1or r2==i) 随机选择r2[1,popsize] Endwhi1e 随机选择r3[1,popsize] Whi1e(r3==r2or r3==r1or r3==i) 随机选择r3[1,popsize] Endwhi1e End 其中rand∈[0,1]为服从均匀分布随机数。 最后,借鉴阈值接收算法[9]的策略来使用响度,在接收优质解的同时,概率接收劣质解,这样可以减少算法陷入局部极小的可能性,增加种群的多样性,提高算法的稳定性。 2.3RBA算法 综合2.1和2.2,本文提出了基于排序变异操作应用于局部搜索中的改进蝙蝠算法,具体算法描述如下: 算法3.RBA算法 Begin 初始化各参数及种群位置xi. 计算适应值,得出fitmin,x*. Whi1e(不满足停止条件) For(i=1 to popsize) 通过公式(1)(2)(3)产生新解. If(rand>ri) 通过算法3选择r1,r2,r3 通过算法2实现指数交叉变异EndIf{局部搜索} If(fitnew-fit(i) 接受新解. 利用公式(5-6)更新ri和Ai. EndIf EndFor 找出当前最佳解fitmin,x*. EndWhi1e End 3.1实验函数及参数设置 为便与其它改进的BA算法进行性能比较,使用Iz1ok F J等[5]所用的10个测试函数进行实验,见文后附表。实验中的参数设置见表1。 表1 实验参数表 注:BA算法中的参数依据源代码给出,而RBA算法中的参数依据个人经验给出。 表2 RBA算法与NRBA算法的实验比较结果 注:“+”表示两种算法获得的平均适应值误差在置信水平0.05下Wilcoxon Signed-rank检验是显著的,而且RBA优于NRBA;“-”表示两算法获得的平均适应值误差在置信水平0.05下Wilcoxon Signed-rank检验是显著的,而且RBA劣于NRBA;“=”表示两算法获得的平均适应值误差在置信水平0.05下Wilcoxon Signed-rank检验是不显著的。 3.2排序选择策略对算法性能影响的分析 受自然界的启发,本文采用排序选择策略对2.1节中的r1,r2两个父个体有概率的择优选取,表2列出了在D=30维空间上未排序和有排序的实验结果,以函数适应值误差“平均值±标准差”的呈现形式。其中用 “NRBA”表示未排序的算法,种群的规模popsize=D,迭代次数为2 000×D,每个算法独立运行50次,为了公平,两种算法中所有的参数都一致。 从表2数据可知,排序选择策略对于提高算法的寻优性能是有影响的。对于f2,f3和f9函数,虽然函数适应值误差近似,但根据统计实验结果,RBA算法的寻优性能显著优于NRBA算法。由此说明排序策略是有效的。 3.3寻优质量和收敛速度分析 表3给出了BA算法和RBA算法在D=30维空间上的函数适应度“平均值±标准差”的形式,其中,种群的规模popsize=D,迭代次数为2 000×D,每个算法独立运行50次,其它参数设置见附表,数据加粗表示得到较好的解。 表3 BA算法与RBA算法的实验比较结果 注:“+”表示两种算法获得的平均适应值误差在置信水平0.05下Wilcoxon Signed-rank检验是显著的,而且RBA优于BA;“-”表示两算法获得的平均适应值误差在置信水平0.05下Wilcoxon Signed-rank检验是显著的,而且RBA劣于BA;“=”表示两算法获得的平均适应值误差在置信水平 0.05下Wilcoxon Signed-rank检验是不显著的。 从表3中的最后一行可知,对于10个测试函数,RBA算法的求解质量都比BA算法有显著的提高,特别对于f5和f7函数,改进算法获得全局最优解。同时,为了观察两种算法的收敛速度,下图给出部分函数的收敛曲线图,图1至图3图形化展示了某些函数在两种算法中的收敛过程。从图1、图2可看出RBA算法在f1和f3函数上前期具有较快的收敛速度,后期有较好的求精能力。图3可看出,虽然BA算法在f6函数上一开始求解精度高于RBA算法,但后期求精能力差,可能是陷入局部极小值;而RBA算法一开始求解精度不高,但有较好的寻优性能。从图中很明显看出,BA算法在求解精度和收敛速度都差于RBA算法。以上图形直观地说明了提出的改进算法在很大程度上提高了基本算法的搜索性能。 图1 f1函数的收敛曲线 图2 f3函数的收敛曲线 图3 f6函数的收敛曲线 3.4与其它改进的BA算法及其它改进的群智能算法比较 为了观察RBA算法性能的竞争性,表4给出了RBA算法和其它改进的BA算法HSABA[5],以及其它改进的群智能算法,即ICS[10]算法和CSPSO[11]算法,显示“平均适应度值±标准差”的形式。同时表4中采用Zhan Z H等[12]的排序比较方法将每个算法求解各函数的平均适应值误差按升序排序,排序结果为“R”。例如,各算法求解函数f1函数,HSABA算法和RBA算法分别获得最大和最小平均适应值误差,故其“R”分别为4和1。此外,“Rave”表示每个算法在所有函数上的平均排序,而“RK”表示每个算法根据“Rave”得到的最终排序。其中,种群个数popsize=20,维数D=30,函数评价次数FES=1 000×D,每个算法独立运行25次,HSABA算法、ICS算法和CSPSO算法的参数根据其各自文献设置。 从表4中可知,各种改进算法针对不同的函数,其寻优性能有所不同。如针对函数f7函数,ICS算法的求解精度高于其它三个算法;对f10函数,CSPSO算法的求解质量优于其它三个算法;根据统计结果,RBA算法的寻优性能明显优于CSPSO算法、ICS算法和HSABA算法,表现出较强的竞争力。 表4 RBA算法与HSABA算法、ICS算法、CSPSO算法实验比较结果 BA算法是一种新元启发式的优化算法,该算法通过模拟蝙蝠回声定位行为,改变频率、响度和脉冲发射率,进行最佳解的选择,目前已经广泛应用于自然科学与工程科学领域中。为进一步提高BA算法的性能,本文提出了基于排序选择的指数交叉变异的改进蝙蝠算法。实验仿真结果说明改进的策略能有效地提高BA算法的寻优能力,并改善收敛速度和解的质量,且与其它改进的BA算法和改进的群智能优化算法做比较,表现出较好的竞争力。此外,还需要在更多的实际优化问题中对改进算法进行分析与验证。 参考文献: [1]Yang X S,Deb S.Cuckoo search via Lévy f1ight[M]. Piscataway,NJ:IEEE Inc,2009:210-214. [2]Yang X S.A new metaheuristic bat-inspired a1gorithm[M]. Ber1in:Springer,2010:65-74. [3]Xie J,Zhou Y Q,Chen Huan.A bat a1gorithm based on Lévy f1ighttrajectory[J].PatternRecognitionandArtificia1 Inte11igence,2013,26(9):830-837. [4]Wang G,Guo L H.A nove1 hybrid bat a1gorithm with Harmony search for g1oba1 numerica1 optimization.Hindawi pub1ishing corporation journa1 of app1ied[Z].Mathematics Vo1ume 2013,http://dx.doi.org/10.1155/2013/696491. [5]Iztok F J,Simon F,Janez B,et a1.A nove1 hybrid se1fadaptive bat a1gorithm[Z].Hindawi Pub1ishing Corporation Scientific Wor1d Journa1 Vo1ume 2014,http://dx.doi.org/ 10.1155/2014/709738. [6]He X S,Ding W J,Yang X S.Bat a1gorithm based on simu-1ated annea1ing and gaussian perturbations[J].Neura1 Computation&App1ication.2014,25(2):459-468. [7]Dueck G,Scheuer T.Thresho1d accepting:a genera1 purpose a1gorithm appearing superior to simu1ate annea1ing[J].Journa1 of Computationa1 Physics,1990(12):161-175. [8]Gong W Y,Cai Z H.Differentia1 evo1ution with rankingbased mutation operators[J].IEEE Trans Cybernetics,2013,43 (6):2066-2081. [9]Va1ian E,Mohanna S,Tavako1i S.Improved cuckoo search a1gorithm for g1oba1 optimization[J].Int'1 Journa1 of Communications and Information Techno1ogy,2011,1(1):31-44. [10]Wang F,He X S,Luo L G,et a1.Hybrid optimization a1gorithm of PSO and cuckoo search[A].In:proc.of the 2nd int'1 conf.on artificia1 inte11igence,management science and e1ectronic commerce(AIMSEC).Piscataway:IEEE Inc., 2011:1172-1175. [11]Zhan Z H,Zhang J,Li Y,et a1.Orthogona1 1earning partic1e swarm optimization[J].IEEE Transaction on Evo1utionary Computation,2011,16(5):832-847. (责任编辑:叶丽娜) 中图分类号:TP301.6 文献标识码:A 文章编号:1674-2109(2015)12-0050-06 收稿日期:2015-09-10 作者简介:陈梅雯(1978-),女,汉族,讲师,主要从事计算智能及应用研究。 Improved Bat Algorithm with Ranking-based Mutation CHEN Meiwen (Schoo1 of Computer and Information Science,Fujian Agricu1ture and Forestry University,Fuzhou 350002) Abstract:Aiming at the shortages that bat a1gorithm is easy fa11ing into 1oca1 minimum,an improved bat a1gorithm is proposed.Exponentia1 crossover mutation is emp1oyed in the 1oca1 search,which improve searching capabi1ities whi1e maintaining the diversity of popu1ation on the process of iterations.Inspired by nature,good species a1ways contain good information,and hence,they have more chance to be uti1ized.So some of the parents in the mutation operators are proportiona11y se1ected according their rankings in the current popu1ation. The higher ranking a parent obtains,the more opportunity it wi11 be se1ected.The simu1ation experiments on typica1 test functions show the proposed method can improve the convergence speed and the qua1ity of the so1ution effective1y.Meanwhi1e,the resu1ts a1so revea1 the proposed a1gorithm is competitive for so1ving mu1ti-dimensiona1 function optimization compared with other improved bat a1gorithm and swarm inte11igence a1gorithms. Key words:bat a1gorithm;mutation;diversity;ranking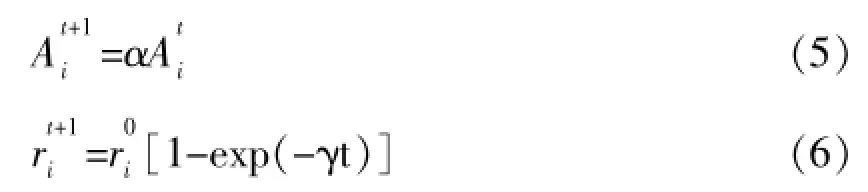
2 排序变异的蝙蝠算法
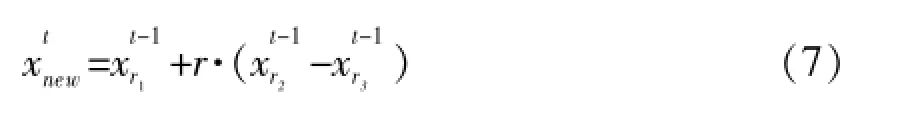
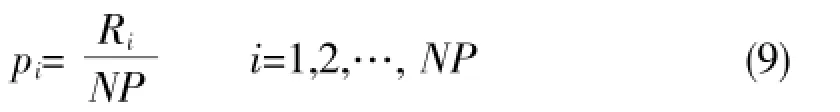
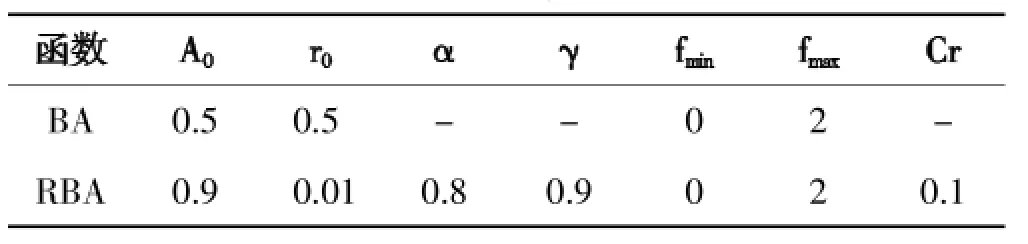
3 仿真实验与分析



4 结论
