当前行为金融研究中数学建模应用的价值分析

2015-08-01南开大学马思远

财经界(学术版) 2015年1期

南开大学　马思远

南开大学马思远

摘要:行为金融学是在传统金融学基础上建立的一种金融理论，能够在理论上弥补个体行为分析的不足和缺陷，当前已经成为一种独立的学科，与数学专业息息相关。与传统的金融体系相比，行为金融学不仅在经济学和数学方面有更深的研究，还涉及到了心理学、行为学以及社会学等，重视决策过程中的人行为以及心理影响。随着行为金融学的不断发展，数学建模手段被广泛的使用，本文先简单分析了行为金融的相关知识，研究数学建模在金融研究中的应用，并以具体的实体分析行为金融中数学建模的应用。

关键词:行为金融学数学建模股指预测

在实际的金融市场中，有很多的现象是传统金融体系所不能解释的，如投资者的意愿以及行为等，在金融系统中，这些是非常重要的影响因素，因此有必要研究投资者的的心理对金融的影响，行为金融应运而生。当前金融用于得到迅速的发展，数学建模的应用极大的推进了金融证券研究的发展，当前在行为学的研究领域中主要的经典理论模式主要是期望理论、DHS模型、BPT模型以及HS模型等，本文主要研究当前行为金融研究中数学建模的使用，希望能为相关人员带来一些帮助。

一、行为金融研究概述

在传统金融理论中，主要包括投资者理论以及市场有效性，在行为金融学中理论基础则不太相同，行为金融学认为信息纰漏不充分、投资者信息的不对称是非常重要的影响因此，市场竞争并不是有效的。在决策的风险测量方法上，行为金融学认为，实际投资者的小于初始资本的结果才是风险，从投资者的心理感受出发，采用变量的实际值的概率表示风险，更加重视投资损失的风险度量方法。从决策模型上分析，行为金融学影响较大的模型包括DHS以及BSV等，认为投资者的行为会导致股价过度反应。

二、期望理论研究

期望理论是行为金融学的基础理论之一，投资者的效应是基于参考点的收益和损失的函数，凸函数才是标准效用函数收益部分。价值函数是期望理论的重要函数，定义中时基于参考点判断盈利，损失比盈利更加陡峭。权重函数也是也是期望理论的重要函数之一，主要是主观判断结果出现概率的大小。通过这两个函数选择具有最大期望值PS的方案。

三、BSV模型研究

BSV模型的建立中，假设投资者在进行决策的过程中，偏差分为选择性偏差（相似性偏差）和保守性偏差，选择性偏差是基于近期数据与模型的相似性来预测，非常重视近期数据。保守性偏差意思是指投资者不能根据信息变化来改变决策，造成保守性偏差，针对这两种误差，建立模型。

模型1qt+1=[(1-λ1)qt+λ2(1-qt)]ΠL/{(1-λ1)qt+λ2(1-qt)+[λ1qt+(1-λ2)(1-qt)] ΠH}描述反应不足，模型2qt+1=[(1-λ1)qt+λ2(1-qt)](1-qt)/{[(1-λ1)qt+λ2(1-qt)] (1-ΠL)+[λ1qt+(1-λ2)(1-qt)](1-ΠH)}描述反应过度。证券价格pt=Nt/δ+yt(pp2qt),此外代表性误差以及保守性误差之间转换遵循讯贝叶斯法则，这个模型的建立能够解释收益惯性等现象。

四、DHS模型研究

投资者在进行投资中会存在反应不足或者是反应过度情况，DHS建立的模型正是建立在了二者统一上，在此模型的建立中，把投资者分为了有信息的投资和无信息的投资两种类型，针对无信息的投资者就不会存在心理偏差，而有信息的投资者会存在过度自行和归因偏差。在投资中，常会出现自我评价过高的问题，低估公开信息所具有的价值。在DHS模型的构建中，当发生噪声的公开信息到来时，无效偏差会得到部分矫正，如果公开信息逐渐增多，就会出现无效偏差反转的情况。把投资者的投资分为4期，0期表示投资者具有相同的先验理念，1期证券价格过度反应，2其引发进一步的交易，3其价格最终回到理论。

1期证券的均衡价格为p1=Ec[θ/θ+ε]=δ2θ(θ+ε)/(δ2θ+δ2c)，2期证券的均衡价格为p2=Ec[θ/θ+ε,θ+η]=δ2θ(δ2c+δ2p)θ/D+δ2θδ2pε/D+δ2θδ2cη/D，价格变化过程见图1所示。

五、HS模型、BCAPM模型和BHS模型研究

HS模型的建立假设消息观测者和惯性交易者，这两种投资者仅仅能够出列公开信息，消息观测者依照信息来对未来基本情况做出预测，受到当前和过去价格的影响。惯性交易者则是完全相反，预测是根据过去的价格变化进行的，在长远的投资中存在反应不足的情况。

AHS模型的建立归纳总结偏差的基础上，投资者在投投资决策中除了直觉偏差之外还存在着框架依赖偏差，前提结果对风险选择存在影响，前提结果的过分依赖就导致投资者的损失。BCAPM模型又可以称为行为资产定价模型，投资者范围内噪声交易者和信息交易者两类，信息交易者不受到认知偏差的影响，不存在严格的偏好。

六、数学建模在行为金融研究中的应用

在这里以股指预测模型为例说明数学建模在行为金融研究中的应用。

(一)行为金融体系的建构

股指波动受到多方面因素的影响，如宏观经济、市场变化等，这些都会影响投资者行为，对股权的走向产生影响。在实际的股票交易市场中，外界的变化会对投资者的心理产生影响，进而改变股指的走向。

在本研究中采用因子分析方法对T检验筛选的治疗进行降维，寻找影响投资者行为的因素。先进行KMO和Battlett检验，KMO值为0.838，可以分析因子。对因子命名方便后期行为指标的因果分析，市场交易因子包括了上期月末指数、上期最低点等，宏观经济因子包括了CPI、资产负债率等指标，市场情绪因子在这里只包括封闭式基金折价率指标，根据不同指标与股指的线性组合关系，判断影响因素，表达式为：

F1=0.102X1+0.465X2+…+0.155X14

F2=0.916X1+0.014X3+…+0.134X14

……

F5=0.240X1+0.134X2+…+0.837X14

筛选出影响股指的五大因子，进行命名，确定经济涵义，为验证因子对上证指数的相关性管理，检验平稳性，若是不具备平稳性，就需要进一步的一阶差分转化为平稳序列，对金融指标进行ADF检验，结果见表1所示。

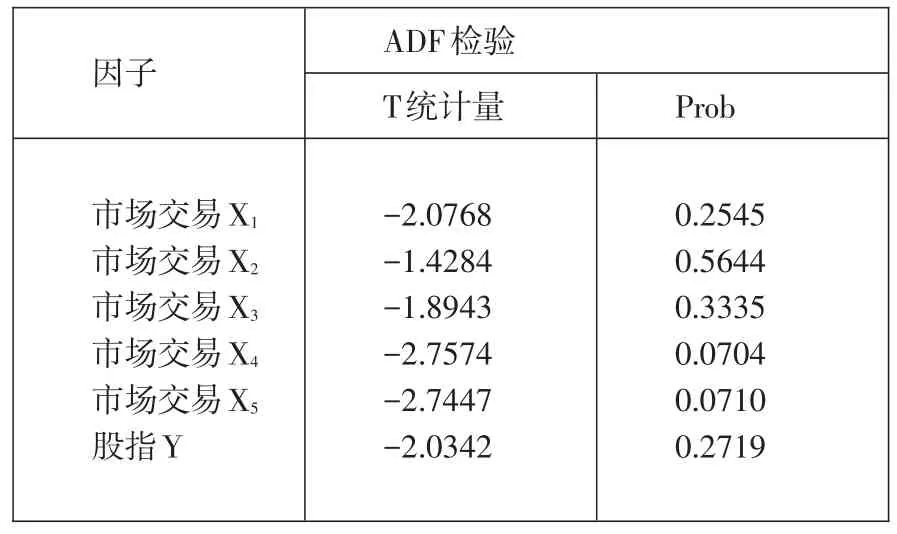
表1　行为金融因子单位根检验结果

行为金融因子全部是非稳定需要采取一阶差分进行SDF检验，各序列的T统计量都高于1%置信下的临界值3.513344，可以采用格兰杰因果检验。基于此建立金融指标体系，影响股指的以及一级行为指标包括市场交易指标、宏观经济指标、货币政策指标、市场情绪指标和市场政策指标，其中市场交易指标包括上期月末指数、上期最高点、机构持股比例等。

(二)股指预测模型的建立

在核函数的确定中需要先确定样本输入输出变量，针对不同阶次的多项式进行比较，再采用RBF核函数对样本数量拟合回归，比较回归拟合结果，确定最佳的核函数。在本研究中评价模型采用的是系数和均方差，在实验前设定不同核函数的SVM模型，选出最佳的损失函数的惩罚参数，通过回归拟合效应发现，径向基RBF核函数构建的股指均方差最小，在此采用RBF核函数。

在当前的非线性预测模型的参数中，还没有统一的理论，需要进行试验，在本研究中采用仿生算法进行优化，确定拟合精确度。先分析每个参数的取值范围，优化选取模型的参数，设定适应度函数，再检验参数选取的效果。结果表明在[0.01,1]范围内，MSE随着ε值的增大而增大，在这里ε定为0.01。

应用遗传算法前需要先设定参数，应用粒子群算设定参数，加速度因袭c1=c2=1.5，最大迭代次数200情况下模型的拟合效果最佳，优化后所获的参数C=3，δ=0.7176.应用基于遗传算法优化的SVM股指预测模型，训练和预测行为金融指标样本数据，先利用输出变量的原始数据进行预处理，将输出数据分为测试样本和训练样本，筛选出核函数作为模型，建立最佳数值构建预测模型，再进行数据拟合预测。基于支持向量机的股权预测建立的模型，获取预测结果，见图2所示，有非常好的拟合结果，但是也能够看出第4和第15个样本值之间存在偏差，模型还需要进一步的完善。

基于BP神经网络的模型在建设中采用单一隐含层建立神经网络模型，输入层神经节点共5个，变量是月末上证股指，在此建立的模型综采用的传递函数以及学习函数等是常见的隐含层含住。神经网络训练隐含层神经节点（4～15）的训练误差分别为0.0016、0.0019、0.0014、0.0012、0.0014、0.0015、0.0011、0.0012、0.0016、0.0013、0.0016、0.0015. BP神经网络建模模型在拟合中存在一些问题，预测不准确。

表2　不同方法对上证股指月末值的预测

基于Elman神经网络的股指预测建立模型与BP神经网络方法比较类似，输出神经节点数目同样为5，传递函数选择为newelm和elmannet函数，elman网络训练隐含层神经节点（4～15）的训练误差分别为0.0017、0.0019、0.0017、0.0019、0.0011、0.0013、0.0012、0.0017、0.0012、0.0017、0.0018、0.0014.预测效果不佳，不能正确反映股指的波动性。以上三种方法分别非测试样本值进行拟合，结果见表2所示，支持向量机预测数据与真实值之间最为接近，预测效果最好。