基于内模控制的工业控制系统仿真器鲁棒PID控制器设计

王佳伟,杨亚非,钱玉恒,赵新宇

(哈尔滨工业大学 飞行器控制实验教学中心,黑龙江 哈尔滨 150001)

基于内模控制的工业控制系统仿真器鲁棒PID控制器设计

王佳伟,杨亚非,钱玉恒,赵新宇

(哈尔滨工业大学 飞行器控制实验教学中心,黑龙江 哈尔滨 150001)

内模控制是一种基于被控对象数学模型的新型控制器设计方法,所设计的控制器具有鲁棒性强、参数整定方便等优点,已经在一些工业场合中得到了应用。为了提高学生对于内模控制方法的理解水平,该文首先简要介绍了内模控制的基本原理和内模PID控制器设计方法,介绍了工业系统仿真器实验平台的构成,并推导了其数学模型的表达式,然后利用内模控制原理为其设计了鲁棒PID控制器,通过仿真软件进行了实验验证,结果证明了内模控制方法的有效性。

内模控制;工业控制系统仿真器;鲁棒PID;控制器设计

内模控制(internal model control,IMC)是一种基于过程数学模型设计的新型控制策略,被广泛应用于现代控制系统,是一种实用的先进控制算法。内模控制的特点是设计简单，参数整定直观、方便，鲁棒性强,并且对纯滞后有补偿作用,所在工程控制领域受到重视[1-4]。近年来,内模控制已被应用于多变量系统和非线性系统。基于内模控制原理设计的PID控制器在鲁棒性上要优于一般的PID控制器,是目前一种流行的鲁棒PID控制器设计方法。

工业控制系统仿真器可以模拟现代工业中使用的许多设备,例如:主轴传动机构[5]、单轴转台[6-8]、输送带[9-10]、机床[11-13]、自动装配机器[14-15],模拟这些设备的控制性能以及加入摩擦、改变齿轮间隙[16-17]或加入扰动后系统的响应情况。本文把工业控制系统仿真器配置为刚体模型,使用内模原理为其设计鲁棒PID控制器。通过这一过程,使学生掌握工业系统仿真器的控制原理及控制算法,为进一步研究工业系统的控制方法打下基础。

1 内模控制原理

典型的内模控制结构如图1所示,其中,P(s)为被控过程,M(s)为被控过程的数学模型,即内部模型,Q(s)为内模控制器,r、y和d分别为控制系统的输入、输出和干扰信号。控制目标是保持y逼近参考值r。D(s)表示扰动对输出的影响。

图1 内模控制原理结构

为求取输入r与过程输出y之间的传递函数,可以先将图1等效变换为图2所示的经典反馈控制形式,图中虚线内为等效的反馈控制器C(s)。

图2 等效反馈控制系统结构

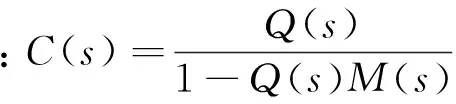
2 内模PID控制器的设计

为了得到内模PID控制器,采用三步法设计:第一步是对过程模型的分解;第二步是针对控制系统模型的不确定性进行鲁棒稳定性和鲁棒性能的设计,主要是通过加入低通滤波环节F(s)来实现;第三步是得到包含内模控制器Q(s)和过程模型M(s)的等效反馈控制器C(s),并将其展开为理想PID的结构,得到P、I、D参数。

步骤1:过程模型M(s)的分解。

M(s)可分解成两项:M+(s)和M-(s),有:

M(s)=M+(s)×M-(s)

步骤2:内模控制器Q(s)设计。

在设计内模控制器时,需在最小相位的M-(s)上增加低通滤波器F(s),以确保系统的稳定性和鲁棒性。定义内模控制器为:

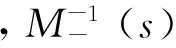
步骤3:内模PID控制器设计。

根据内模控制器Q(s)和过程模型M(s)设计等价反馈控制器C(s):

其中

将f(s)进行Taylor级数展开,可以得到

其中K=f′(0),Ti=f′(0)/f(0),Td=f″(0)/2f′(0)

理想的PID控制器具有如下算式:

按照上面的理想PID控制器结构,将设计好的反馈控制器C(s)进行Taylor级数展开,根据Taylor近似的方法,则可以得到P、I、D三个参数的表达式,他们都与滤波器参数λ有关。

3 工业系统仿真器及其数学模型

该实验装置由图3所示的3个子系统组成:(1)工业系统仿真器的机械部分;(2)基于M56000处理器系列DSP的控制系统,能够以高采样率执行控制律、解释轨迹命令,并支持数据采集、轨迹生成、系统状态及安全检测等功能;(3)系统执行程序,它是系统的用户界面,支持控制器指定、轨迹定义、数据采集、绘图系统执行指令等。

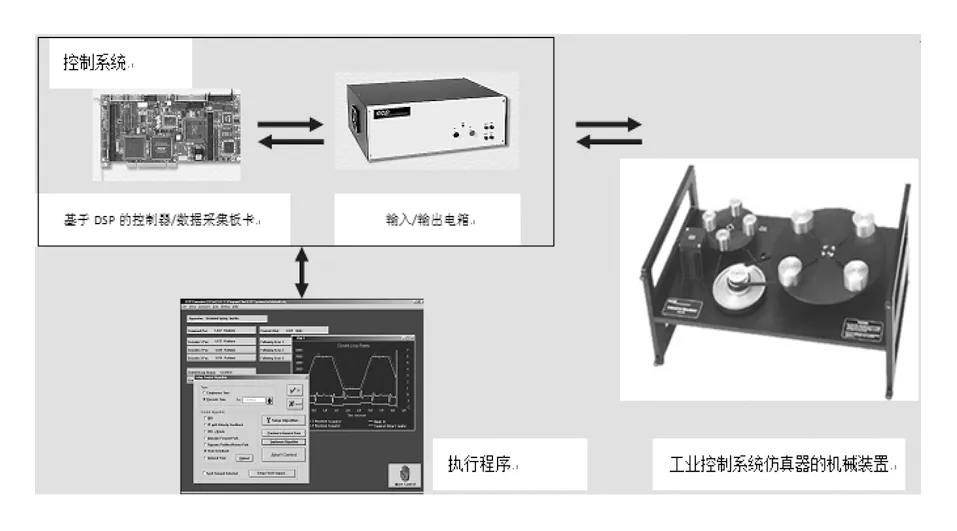
图3 工业控制系统仿真器装置组成

工业控制系统仿真器的机械装置由1个无刷直流伺服驱动电机和2个惯量可调的圆盘(其中1个驱动圆盘,1个负载圆盘)组成(见图4、图5)。伺服电机通过同步皮带与驱动圆盘连接,驱动圆盘通过同步皮带与减速装置连接,传动齿轮组通过同步皮带与负载圆盘连接。负载圆盘与驱动圆盘的惯量变化,可通过加入或移走其上的黄铜砝码来实现。

图4 工业控制系统仿真器的机械部分

图5 简化的动力分析

当忽略驱动器的柔性、齿隙等一些非理想因素或其他非线性因素对系统的影响时,可以将系统看作简单刚体,从而把摩擦看成是黏性的,并从图5推出

和

传递函数为:

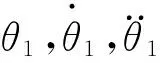
4 控制器参数计算及仿真验证

4.1 控制器参数计算

被控部分数学模型为

根据第2节中的内模PID控制设计方法,得到内模控制器Q(s)为

和等价反馈控制器

将C(s)看作PID控制器的形式,则相应的参数为

微分系数等于0是由于对象中没有滞后环节的存在,其余的P、I两个参数的表达式,都与滤波器参数λ有关。

4.2 仿真验证

使用Matlab软件中的Simulink进行仿真,构建闭环框图如图6所示,图7—图9是λ为不同值时系统的阶跃响应曲线。

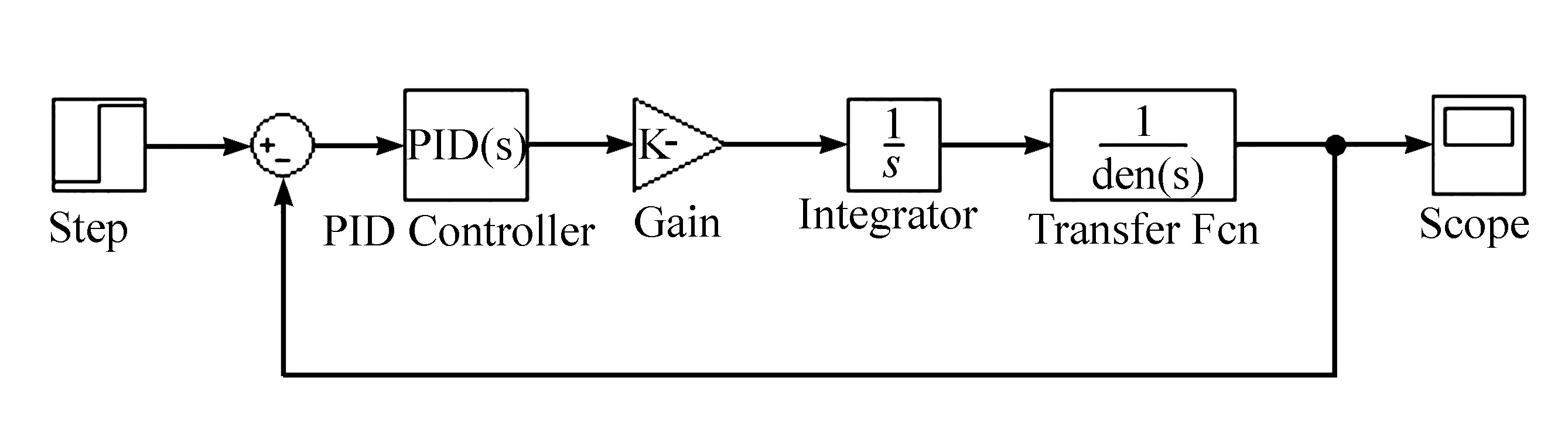
图6 Simulink中的闭环框图

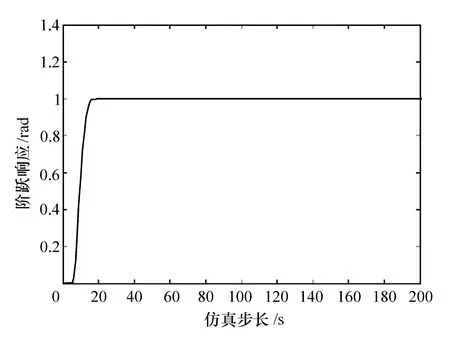
图7 λ=0.05时系统的阶跃响应曲线

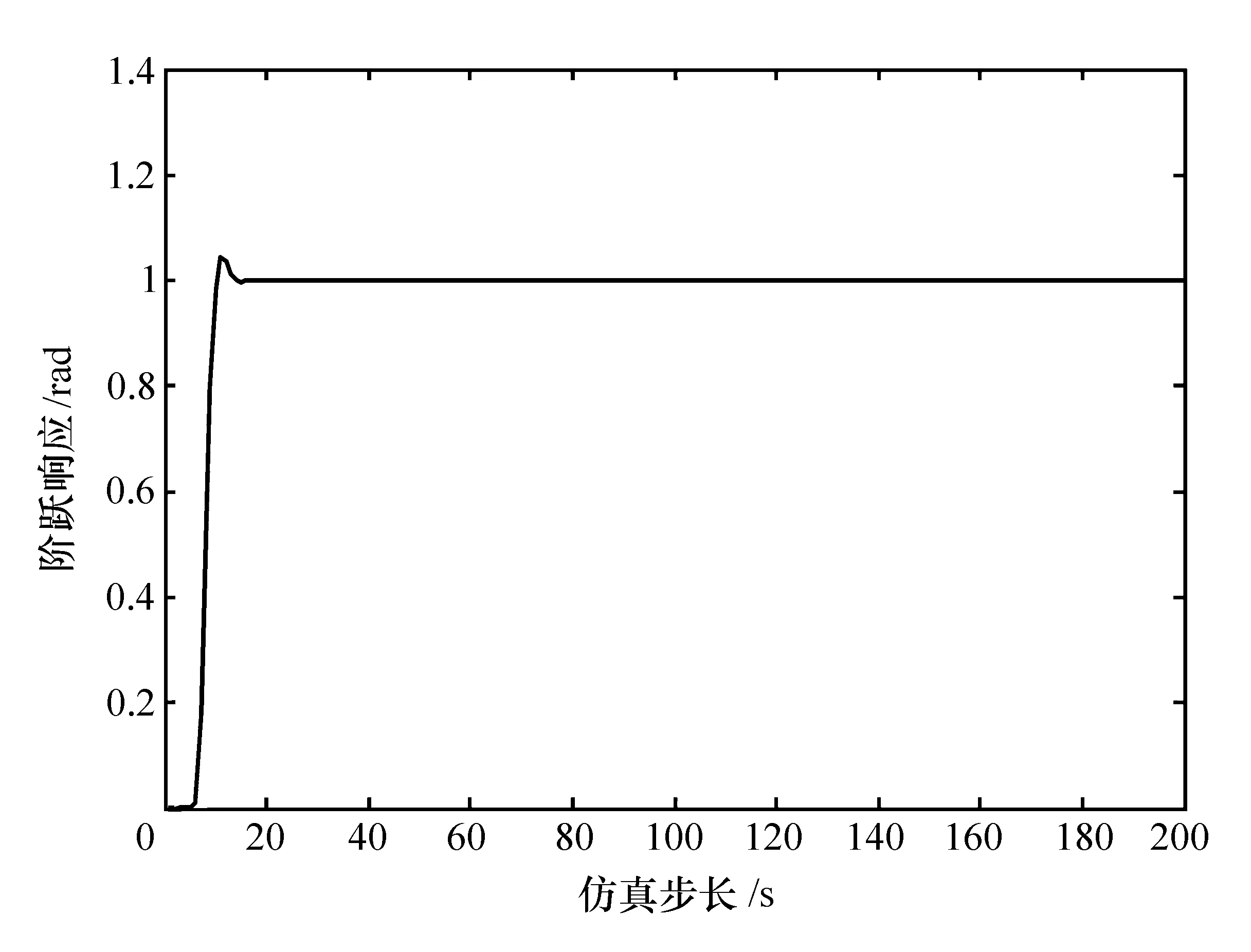
图8 λ=0.02时系统的阶跃响应曲线

图9 λ=0.01时系统的阶跃响应曲线

比较可知,当λ=1时,虽然没有超调量,但反应时间过长;当λ=0.01时,反应时间虽短,但系统超调量较大。相比较而言,当λ=0.02时,不但响应时间短,而且超调量也不高,效果比较好。

5 结束语

内模控制方法是一种基于控制对象数学模型的控制方法,使用其设计的PID控制器的调节参数只有一个,因此参数整定十分容易。除了文中提到的PID方法,内模控制还可以和其他控制方式相结合,进一步改进控制的性能。在应用方面,除了文中的单变量线性系统,内模控制还可以推广到多变量系统和非线性系统中,这些都是以后值得关注的发展方向。

)

[1] 郑泳凌,马龙华,钱积新.鲁棒PID控制器参数整定方法[J].化工自动化及仪表,2001,28(5):14-16.

[2] 李会军,陈明军.基于LMI的H_∞鲁棒PID控制器设计[J].控制工程,2007,14(3):294-296,315.

[3] 张艳兵,王忠庆,姚舜才.基于极小极大原理的内模PID控制器研究[J].测试技术学报,2007,21(2):1-4.

[4] 彭利标,赵辉.基于内模控制原理整定PID参数[J].天津理工大学学报,2009,25(5):1-2.

[5] 杨金鹏,尹存涛,章鸿,等.全齿轮传动主轴的软起节能运行制动器设计[J].新技术新工艺,2012(12):63-65.

[6] 邓正隆,王爽.陀螺漂移测试转台的发展和展望[J].宇航学报,1987(3):91-95.

[7] 宋桂云.常用陀螺测试系统[J].有色金属,2005,57(2):128-130.

[8] 吴南江.一种单轴测试转台设计[J].伺服控制,2007(11):61-62.

[9] 朱立平,韩东劲,许静泉.输送带的动力学模型[J].煤矿机械,2001(2):29-30.

[10] 周广林,陈健,罗凤利,等.输送带的粘弹力学特性[J].煤矿机械,2001(12):22-24.

[11] 覃文洁,左正兴,刘玉桐,等.机床整机的动态特性分析[J].机械设计,2000(10):24-26.

[12] 李军锋,李剑,席平.数控机床加工仿真技术及应用[J].计算机仿真,2003,20(4):92-94.

[13] 孔杰,覃岭.数控车床主轴传动系统的动力学优化设计[J].机械传动,2012,36(7):59-61.

[14] 谢永宏,朱梅,李绍炎,等.自动装配生产线教学演示系统设计研制[J].深圳职业技术学院学报,2004(2):30-33.

[15] 强小拾,罗庚合.机电一体化自动装配教学生产线的应用[J].西安航空技术高等专科学校学报,2009,27(3):63-65.

[16] 李丹.传动装置齿隙位置对伺服系统的影响[J].重型机械科技,2004(2):26-31.

[17] 周金柱,段宝岩,黄进.含有齿隙伺服系统的建模与对开环频率特性的影响[J].中国机械工程,2009,20(14):1722-1726.

Design of robust PID controller for industrial control system emulator based on internal model control

Wang Jiawei,Yang Yafei,Qian Yuheng,Zhao Xinyu

(Experiment and Teaching Center for Flight Vehicle Control,Harbin Institute of Technology,Harbin 150001,China)

The internal model control is a kind of novel control theory,which is based on model of the controlled object. The robustness of designed controller is strong and the procedure of parameter setting is convenient. It has been applied in some industrial situation. In order to improve the students’ understanding of the internal model control method,the principle of internal model control and the method of designing the internal PID controller are introduced briefly. Then,the hardware structure of industrial control system emulator is given and the mathematic model of industrial control system emulator is derived. For the equipment,the robust PID controller is designed,and tested by simulation software.Lastly,the simulation figures show the effectiveness of internal model control method.

internal model control ;industrial control system emulator;robust PID;design of controller

2014- 05- 09

黑龙江省教学研究项目(JG2013010268)

王佳伟(1982—),男,黑龙江哈尔滨,在读博士研究生,工程师,研究方向为控制系统实验与故障诊断技术.

E-mail：wangjiawei1982@163.com

TP271

A

1002-4956(2015)1- 0120- 04