机器学习在党政干部日常考核模型权重赋值中的运用

秦博+徐浩铭

〔摘要〕机器学习方法在领导干部日常考核指标体系设置中被广泛运用。层次结构模型（AHP&FAHP）的基本思路是将复杂问题分解为若干层次和若干要素，通过简单比较、判断和计算，获得不同要素的权重，最后通过加权求和做出最优选择。而SVM作为一种新兴的机器学习方法，也逐渐被引入到领导干部日常考核的指标设计之中。SVM的原则是结构风险最小化，在样本分类误差尽可能小的前提下，充分提高分类器的泛化推广能力，这有助于解决小样本、非线性以及高维模式识别问题;文章总结和比较了AHP、FAHP、SVM三种模型的理论基础和基本方法，试图为领导干部日常考核提供理论依据。

〔关键词〕机器学习;干部考核;权重赋值;层次结构模型;支持向量机模型

〔中图分类号〕D630.3〔文献标识码〕A〔文章编号〕2095-8048-（2015）03-0028-04

一、 引言

理解机器学习的关键概念是学习，然而对于学习这个概念迄今却无精准定义。不同的学科对机器学习的研究侧重不同，其机理和实现很难把握，因为学习是一种综合性、多侧面的心理活动。机器学习是人工智能领域内的重要分支，虽然已经被广泛应用于科学领域，但是在社会科学领域的应用相对较少，对于干部考核这一块少有文献。事实上，机器学习方法能够应用于干部考核。如何科学地权重赋值是建立干部考核体系的技术重点和难点。过去的干部考核方法在为考核因素排序时，往往基于常规的统计分析和定性的经验来赋予不同因素以不同的权重，进而调整不同频度的排序算法。此类方法的缺陷首先在于不能容纳较多的排序因素，否则会致使调整权值变得非常复杂。其次此类方法无法有效应对新的排序因素，因为通常都缺少对这一数据的直观经验，单凭经验不能妥当权衡这些因素的权重。较之于以往的方法，基于机器学习的排序技术就可以弥补缺陷，因为机器学习技术可以引入大量的排序因素，能够快速适应新的权重分配和排序策略，而且无需手动调整各因素的权值。

党政领导干部考核评价工作的基础是设置科学合理的考核评价指标体系，而指标体系的科学与否直接关系到考评的质量和结果。根据《党政领导干部选拔任用工作条例》、《党政领导干部考核工作暂行规定》等相关规定，当前对党政领导干部考核评价内容主要分为 “德、能、勤、绩、廉”五方面，再结合各个部门职能要求以及现阶段发展方向和中心等，设立相应的二级指标乃至三、四级指标。

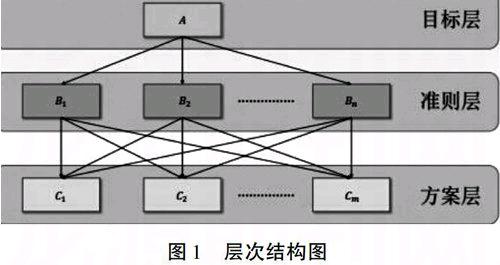
图1层次结构图

图2领导干部日常考核指标层次结构图

考核评判结果分为五个层次，即“好，较好，一般，较差，差”。

指标确立后的重要工作是权重赋值。权重是评价过程中通过不同侧面的重要程度来对评价对象的定量分配，并对各评价因子在总体评价中的作用区别对待。在之前的领导干部考评之中，对于权重的设计虽然已经逐渐引起重视，但仍停留在凭经验分配的阶段，各个地区和部门的权重赋值也是大相径庭的。对某个具体指标过度强调或者过度弱化都可能产生结果上的偏差，因此考核权重的设计对于工作行为来说是至关重要的步骤。换言之，权重设计是测量干部考核绩效和干部真实绩效是否一致的准绳，将权重系数用来调节各类各级干部的特殊性，能够增强考核结果的科学性和可比性。因此，在如今的领导干部日常工作考评体系之中，权重赋值应成为重要环节。

现在普遍的方法是以绩效评估现有理论与方法为基础，通过对党员领导干部考核的各项指标进行打分，应用机器学习，统计分析进行分析和研究，建立考核模型。层次分析法（AHP）和模糊层次分析法（FAHP）是提高权重系数精确测度的比较有代表性的、较成功的方法，在干部日常考核体系中广泛应用，其基本思路是将复杂问题分解为若干层次和若干要素，通过简单比较、判断和计算，获得不同要素的权重，然后通过加权求和做出最优选择，这样一来可以使得考评标准规范，又能让计算方法公开合理，还能使考核体系简便实用。而SVM是一种较新的机器学习方法，它的原则是结构风险最小化，使样本分类误差尽可能小的前提下，充分提高分类器的泛化推广能力。因其在解决小样本、非线性以及高维模式识别问题中表现出许多特有的优点，也逐渐被引入到领导干部日常考核的指标设计之中。本文总结和比较了AHP、FAHP、SVM三种模型的理论基础和基本方法，试图为领导干部日常考核提供理论依据。

二、 层次结构模型（AHP&FAHP）

（一）层次分析法（AHP）

对于准则层B，需要通过对因素c1，c2，…，cn进行两两对比，并选择标度，构造判断矩阵B。具体含义和标度如下表：

标度  含义  1 表示两个元素相比，具有同等重要性  3 表示两个元素相比，一个元素比另一个元素稍微重要  5 表示两个元素相比，一个元素比另一个元素明显重要  7 表示两个元素相比，一个元素比另一个元素强烈重要 9 表示两个元素相比，一个元素比另一个元素极端重要 2，4，6，8 如果量元素差别介于两者之间，取上述相邻判断的中间值  倒数若元素i与元素j重要性之比为cij，那么元素j元素i的重要性之比为cji=1cij 根据判断矩阵进行求解，以确定各个因素的权重：

Wi=（∏nj=1cij） 1n∑nk=1（∏nj=1cij1n），i∈N                                         （1）

特征向量W = 〔 W1， W2， …， Wn 〕T。上层评价为W T * C。

然后计算判断矩阵的最大特征根

λmax=1n∑ni=1∑njcijWjWi                                                （2）

最终，检验判断矩阵的一致性

CI=λmax-nn-1，CR=CIRI                                      （3）

当CR<0.1时，判断矩阵具有满意的一致性。

（二）模糊层次分析法（FAHP）

模糊层次分析法（FAHP） 是基于层次分析法（AHP）的一种改进模型，模型中采用模糊集取代判断矩阵中的数，对矩阵中的各元素求得模糊权重，采用FAHP，是借鉴了AHP的分层思想，基于模糊集合理论中模糊一致矩阵和模糊一致关系而建立，使模糊决策模型与人们的思维习惯相一致，从而在检验判断矩阵的一致性时更为容易。FAHP模型中因素的两两比较判断，采用一个因素比另一个因素的重要程度定量表示，模糊判断矩阵C=（cij）n*n具有如下性质：

cii=0.5，i∈N

cij+cji=1，cij≥0，i，j∈N（i≠j）

其标度和含义如下：

标度 含义  0.5  表示两个元素相比，具有同等重要性 0.6  表示两个元素相比，一个元素比另一个元素稍微重要  0.7 表示两个元素相比，一个元素比另一个元素明显重要 0.8 表示两个元素相比，一个元素比另一个元素强烈重要  0.9  表示两个元素相比，一个元素比另一个元素极端重要  0.1， 0.2， 0.3， 0.4  若元素i和元素j重要性之比为cij，那么元素j与元素i的重要性之比为cji = 1- cij  对于模糊互补判断矩阵，判断矩阵权重公式如下：

Wi=∑nj=1cij+n2-1n（n-1），i∈N                                      （4）

C的权重向量W=（W1，W2，…Wn）T且∑ni=1Wi=1，Wi≥0（i∈N）

构造特征矩阵元素为：

Wij=WiWi+Wj，i，j∈N

则判断矩阵C的特征矩阵为W=（Wij）n*n。

然后检验模糊特征矩阵与互补判断矩阵的一致性：

I（A，W）=1n∑ni=j∑nj=i|cij+Wji-1|≤a

通过对AHP模型和FAHP模型的描述中可以看出，AHP的计算公式对其结果有缩放作用，所求结果会表现出极端性。而FAHP的计算公式对结果不具有缩放作用，且标度间隔差较小，所求结果难以表现出极端性。换句话说，AHP模型能够很好地体现出元素间的极端重要性，而FAHP模型则能很好地体现出元素间的明显重要性和稍微重要性。因此，在层次分析中可以将两者结合使用。

三、支持向量机模型（SVM）

SVM是根据统计学习理论（SLT）提出的一种机器学习方法，对线性分类器提出了另一种设计最佳准则，是针对在有限样本的情况下，其目标是得到当前信息下的最优解，而不仅仅是样本趋于无限大时的最优值。SVM的原理也从线性可分说起，然后扩展到线性不可分的情况：

图3

其中，实心点表示-1，实心点表示+1。直线方程为f（x）=wx+b，该方程也等价于f（x）=w1x1+w2xx+…+Wnxn+b                             （5）

当向量x=2的时候，表示二维空间中的一条直线;当向量x=3的时候，表示三维空间中的一个平面;当向量n>3的时候，表示n维空间中n-1维超平面。

当有一个新的点x需要加入到预测属于哪个分类的时候，采用就可以预测h（x）。当f（x）>0时，h（x）= +1，当f（x）<0时，h（x）= -1。如图所示：

如下图所示：

从实施的角度来说，SVM应该在样本中建立最优分类面，该分类面使被分开的两类样本的间隔最大，这意味着推广能力最强。如图4：

图4

支持向量位于wx+b=1与wx+b=-1的直线上，支持向量的表示为y（wx+b）=1，y是类别属性。

黑色线表示红色线和蓝色线即支持向量所在的面，而两者之间的间隙就是需要最大化的分类间的间隙M=2w·w=2‖w‖                                   （6）

间隔最大化等价于求||w||，优化求解表达式为

max1‖w‖→min12‖w‖2                                            （7）

其限制条件为

min12‖w‖2s.t.，yi（wTxi+b）≥1，i=1，…n                            （8）

采用拉格朗日乘子法求解，则

L（w，b，a）=12‖W‖2-∑ni=1a（yi（wTxi+b）-1）                         （9）

让L关于w，b最小化，分别令L关于w，b的偏导数为0

Lw=0w=∑ni=1aiyixi

Lw=0∑ni=1aiyi=0（10）

将公式10代入L（w，b，a），得到对偶问题的表达式

L（w，b，a）=12∑ni=1ai-12∑ni，j=1aiajyiyjxiTxj                          （11）

maxa12∑ni=1ai-12∑ni，j=1aiajyiyjxiTxjs.t.，ai≥0，i=1，…n

∑ni=1aiyi=0                                              （12）

在公式12中加入惩罚函数，得

min12‖w‖2+λ∑Ri=1εi，s.t.，yi（wTxi+b）≥1-εi，εi≥0                 （13）

四、结语

本文分析了各种领导干部考核评价和模型的理论基础和方法，主要结论有：第一，现在的考核模型在干部考核评价体系中应用会产生不同的得分结果，但是SVM模型在干部考核预测评价中的准确性较高;第二，如果采用不同的模型对干部进行评价，很难得到一致准确的得分结果，在这样的情况下，我们可以考虑采用分等级评估的办法，例如，我们可以对干部划分五个层面：优秀、良好、合格、较差和不合格。第三，传统经验和主观判断的权重赋值方法应逐步被科学的考核模型和量化方法所取代。第四，在实际考核中，应根据不同的领导岗位，列出不同的考核要素，设计差别化的问卷搜集有用信息对领导干部进行富有针对性的考核。

对于目前普遍流行的领导干部日常考核指标体系来说，仍然存在两个方面的缺陷影响着评价结果的客观和有效。首先是指标的制定和细化仍难以兼顾共性和个性，难以实现全面和简便;其次，指标权重仍主要基于前期的强制分配。从理论上说，这两个影响因素虽然不能完全被消除，但可以尽量缩小，不过需要大量的实践数据反馈来进行验证，而如此一来消耗的人力、物力以及时间又会增加。在实际操作中，一套考核指标权重设计很难适应不同地区以及不同岗位的考核需求，应根据层次分析模型和支持向量机模型的各自特点进行有针对性的灵活运用。 〔参考文献〕

〔1〕中共中央《党政领导干部选拔任用工作条例》

〔2〕曹萍，龚勤林，任泰山.基于AHP的西部地区干部考核评价指标体系构建〔J〕.西南民族大学学报，2012，（12）.

〔3〕胡月星. 推进中国领导人才选拔测评面临的挑战和任务〔J〕. 领导科学，2013，（30）.

〔4〕韩世欣，黄梯云，李一军. 基于机器学习理论的智能决策支持系统模型操纵方法的研究〔J〕.决策与决策支持系统，1996，（1）.

〔5〕李嘉佑，何清，史忠植. 机器学习与网络信息处理〔J〕. 计算机工程应用，2004，（33）.

〔6〕陈可佳. 社会网络分析中的机器学习技术综述〔J〕. 南京邮电大学学报，2011，（3）.

【责任编辑：石本惠】党政研究20153