感应加热钎焊金刚石砂轮过程基体温度场变化分析

张美琴,吴海融

(1.厦门理工学院机械与汽车工程学院,福建厦门 361021; 2.华侨大学制造工程研究院,福建厦门 361021)

感应加热钎焊金刚石砂轮过程基体温度场变化分析

张美琴1,吴海融2

(1.厦门理工学院机械与汽车工程学院,福建厦门 361021; 2.华侨大学制造工程研究院,福建厦门 361021)

文章采用ANSYS有限元方法分析了在高频感应加热钎焊金刚石砂轮时砂轮基体的温度场分布规律。建立感应加热的简化模型,运用磁-热耦合的方法求解计算,分析砂轮基体的温度分布随加热时间、加热功率及位置的变化规律。结果表明,砂轮基体温度随加热快速升高;加热功率越高,加热速度越快,基体内孔和外圆表面的温度差越大,且这差值随着时间的增长而增大。砂轮外圈的应力约为内圈应力的两倍,外圈的热变形最大,内圈的热变形最小。热应力作用下,砂轮的内孔扩大。

钎焊;金刚石;砂轮;感应加热;温度;有限元分析

1 引言

由于钎焊金刚石技术可以改善金刚石、钎料、基体间的结合强度,钎焊金刚石砂轮技术已成为加工金刚石砂轮的重要方式,而钎焊加热方式则是影响钎焊金刚石砂轮质量的重要因素之一[1]。作为钎焊金刚石的加热方式之一,高频感应加热的应用极为广泛。国内外学者围绕着加热工艺展开了大量的研究工作,但主要集中在钎焊工艺上,具体可归结为:①钎焊金刚石界面微观物质研究以及表面碳化物形成的动力学研究;②钎焊工艺的研究(包括钎料类型、钎焊温度、钎焊时间、钎焊的加热方式);③钎焊金刚石工具磨削实验的过程研究(包括对磨削力和能量,金刚石的磨损研究以及工具修整的研究)。但对感应加热过程的基体温度分布却鲜有报道,而这恰恰是提高钎焊料层均匀性、控制磨粒等高性的重要因素之一[2-5]。为了更为直观地了解高频感应加热时砂轮基体的温度分布,本文通过ANSYS有限元仿真分析,总结加热功率、加热时间等对砂轮基体温度分布的影响,以期为感应加热法制作钎焊金刚石砂轮提供参考。

2 ANSYS建模过程

感应加热时交流电磁场在被加热工件中产生的涡流作为内热源影响温度的分布,而温度的变化使材料的性能发生变化进而对电磁场产生影响,温度场和电磁场是双向耦合的,是复杂的多场耦合。为此,本文采用多场求解器法,磁-热耦合场的计算流程如图1所示[6]。

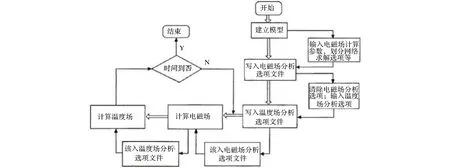
图1 磁-热耦合场的计算流程图Fig.1 The calculation flow chart of magnetic-thermal coupling field

2.1 有限元模型建立

(1)建立轴对称几何模型

图2是有限元分析模型建立示意图。图2a是感应加热钎焊金刚石砂轮的加热模型。由于被加热的基体和感应线圈都呈轴对称结构,基体的电磁场、感生涡流和温度场等的分布也都是轴对称的,假设基体材料均匀连续,可以把实际的空间三维问题简化为二维处理,即取基体截面的1/2部分计算,以提高计算速度。实际感应线圈为空心铜管,但由于在计算中施加的是电流密度载荷,可以用实心代替空心,建立方形实心模型。另外考虑漏磁的影响,需对工件周围的部分空气建模。图2b为简化后的感应加热模型,其中A2是基体,A4是线圈,A1、A3是空气。

(2)定义单元类型

在电磁场分析部分,基体、线圈与空气的网格单元采用相同的PLANE53四边形单元;温度场分析部分,由于只对基体温度分布进行分析,因而采用热分析PLANE55四边形单元。

(3)对截面进行网格划分

由于感应加热时基体上涡流分布具有明显的集肤效应,为确保计算精度,同时为了降低计算量,砂轮基体的网格划分采用映射法划分,越靠近感应线圈部分网格划分越密,网格密度由外表面向中心逐渐递减。其余的部分采用自由网格划分的形式,划分的网格密度适中,网格比较规则,均为四边形网格。整体模型的网格划分和砂轮基体的网格划分分别如图2c所示。

(4)边界条件

电磁场边界条件:假设电流强度通过线圈内侧横截面时是均匀的,线圈部分电流密度的数值可通过式(1)[7]计算得到,该条件同时也是电磁场的激励条件。

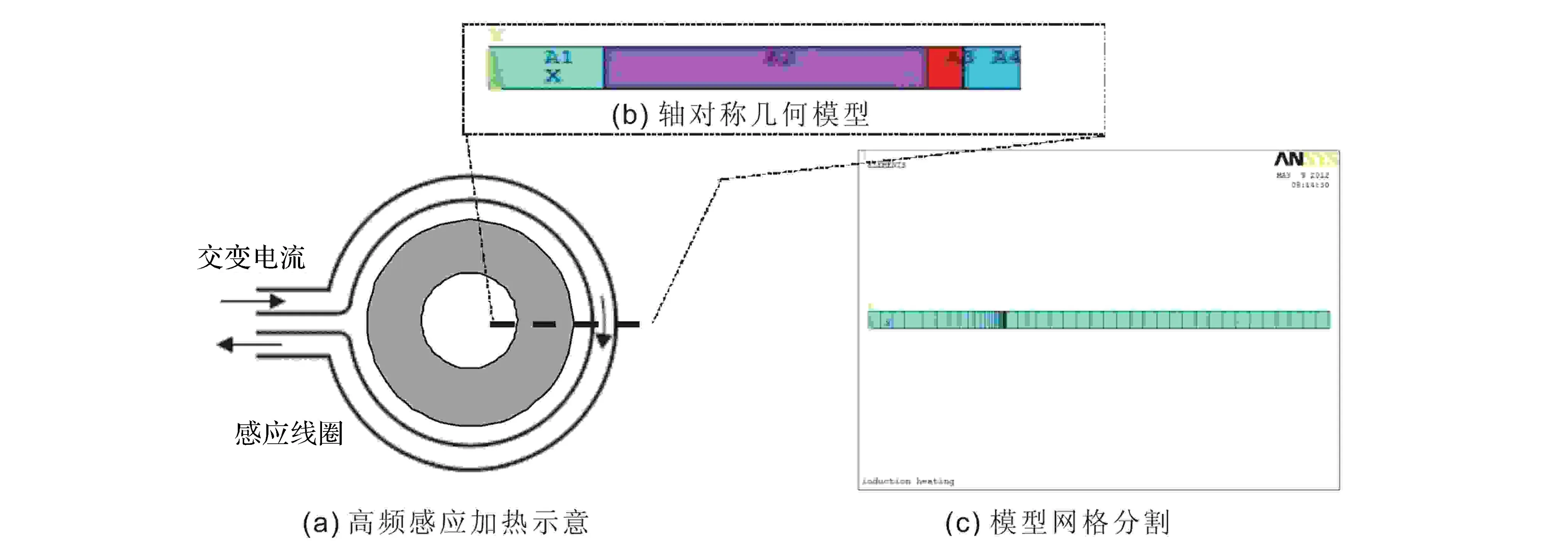
图2 有限元分析模型建立示意图Fig.2 Schematic diagram of finite element modeling

式中:Ie—电流密度;I—线圈电流;N—线圈砸数;ρ—电阻率,μ—工件导磁率,ω—角频率。

热边界条件处理:加热过程中,由于基体与外界存在温度差而与周围介质换热,其中包括对流和辐射换热。在加热过程中,由于基体被包围在感应衬套中,所以对流损失很小。高温下热辐射非常明显,故仿真时假定热损失全部是由辐射产生的。综合各方面因素,本文取辐射率为0.68。

2.2 感应加热工艺参数

砂轮基体材料为45钢,其导热系数、比热容、相对磁导率、电阻率等详见文献[8]。

砂轮规格:外径120mm、内径31.75mm、厚度8mm。

感应线圈:外径146mm、内径130mm、长度1300mm、匝数3,材料T3铜。

电流频率为30k Hz。

3 ANSYS仿真分析结果

3.1 温度场仿真分析结果

图3是感应功率6.4k W(电流密度为930k A/ m2)、加热时间为50s时砂轮基体上温度随时间的变化情况。从图中可以看出,受集肤效应的影响,砂轮外圆表面的温度远要高于内孔的温度,越靠近外圆,温度升高越明显。

图4是同一加热功率下砂轮上沿径向不同半径位置的温度随加热时间的变化趋势。从图中可以看出,越靠近线圈的砂轮基体部分,温度升高越快;基体外圆表面温度升高的速度由快逐渐变慢,而内孔表面温度升高的速度由慢缓慢变快。

图3 加热50s时温度分布云图Fig.3 The could map of temperature distribution when heated for 50s

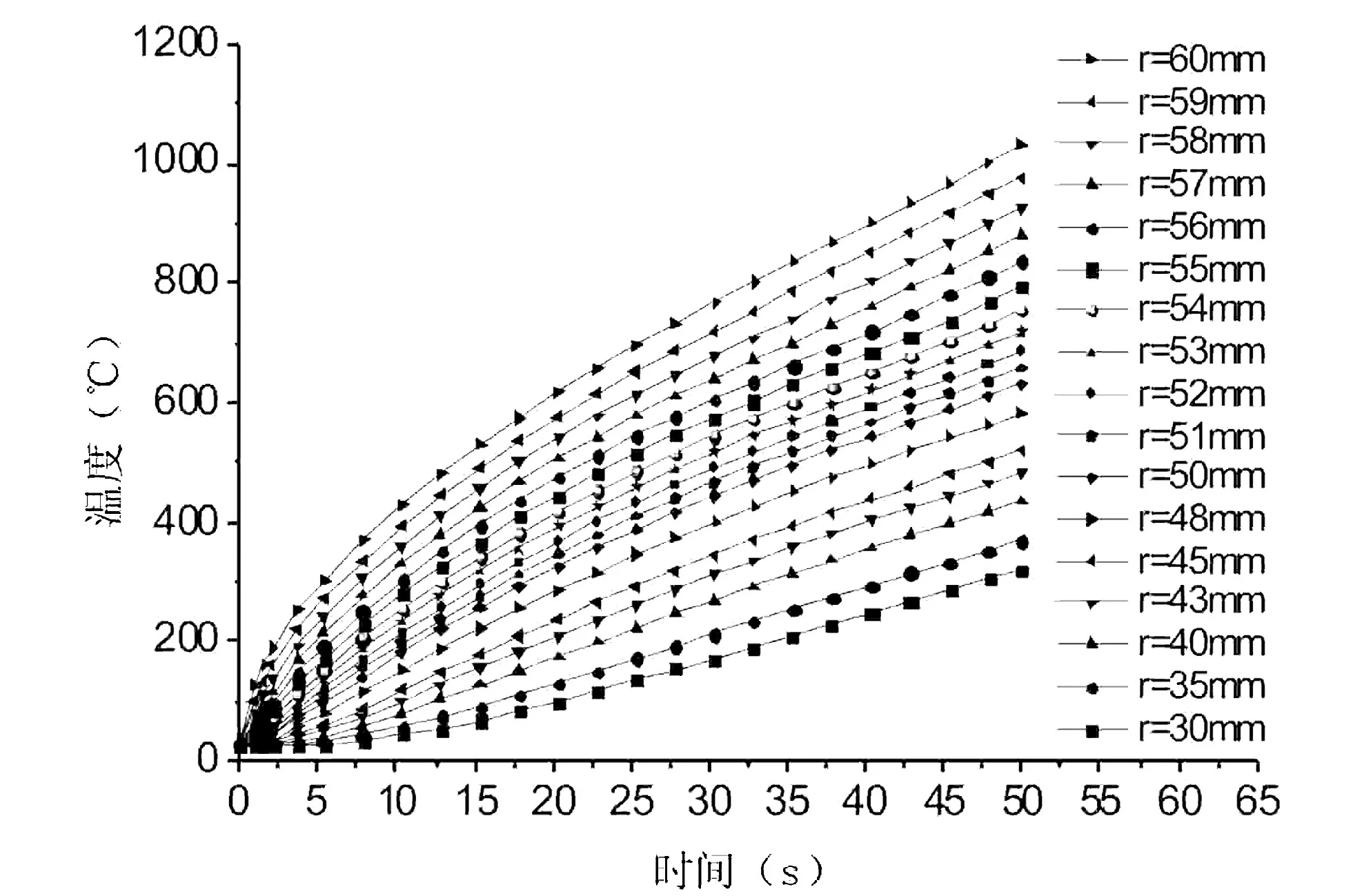
图4 同一功率下砂轮基体不同半径位置温度随时间的变化Fig.4 Temperatures of wheel matrix at different radius position with time changes under the same heating power

图5是当功率分别为6.4k W、8.6k W、10.1k W时砂轮基体内外表面的温度随时间变化曲线。不难看出,三种不同功率下,基体外圆表面的温度随时间变化的曲线差异较大,而内表面的温度变化曲线几乎一致;当加热时间相同时,功率越大基体外圆表面的温度越高,基体内外表面的温度差也越大。

图5 不同功率下砂轮基体r=60和16mm处温度随时间的变化Fig.5 Temperatures of wheel matrix changes with time under the same heating power (r=60mm and 16mm)

3.2 热变形及热应力分析

高频感应加热后砂轮的热变形如图6所示。不难看出,加热后基体内孔扩大。由图6a可知,沿着砂轮轴向同一圆周半径处的变形量相同;而图6b则表明,同一圆周半径处,砂轮基体上下表面的变形量不同,由于下表面受位移约束,所以下表面的变形量比上表面的小。

砂轮基体的径向、轴向、周向应力分布如图7所示。表1是不同加热功率下砂轮基体内外圈的温度、热应力计算结果。不难看出,对于砂轮基体的等效应力,砂轮外圈的应力最大,内圈的应力虽然不是很大,但也不是最小的,约为外圈应力的一半。对于砂轮基体的总变形,在拉应力的作用下,砂轮基体的内孔扩大;基体外圈的变形量最大,内圈的变形量最小;同一圆周半径处上下表面的变形量不一样,上表面的变形量比下表面的稍大;由于受热膨胀,砂轮基体的厚度稍稍有所增加

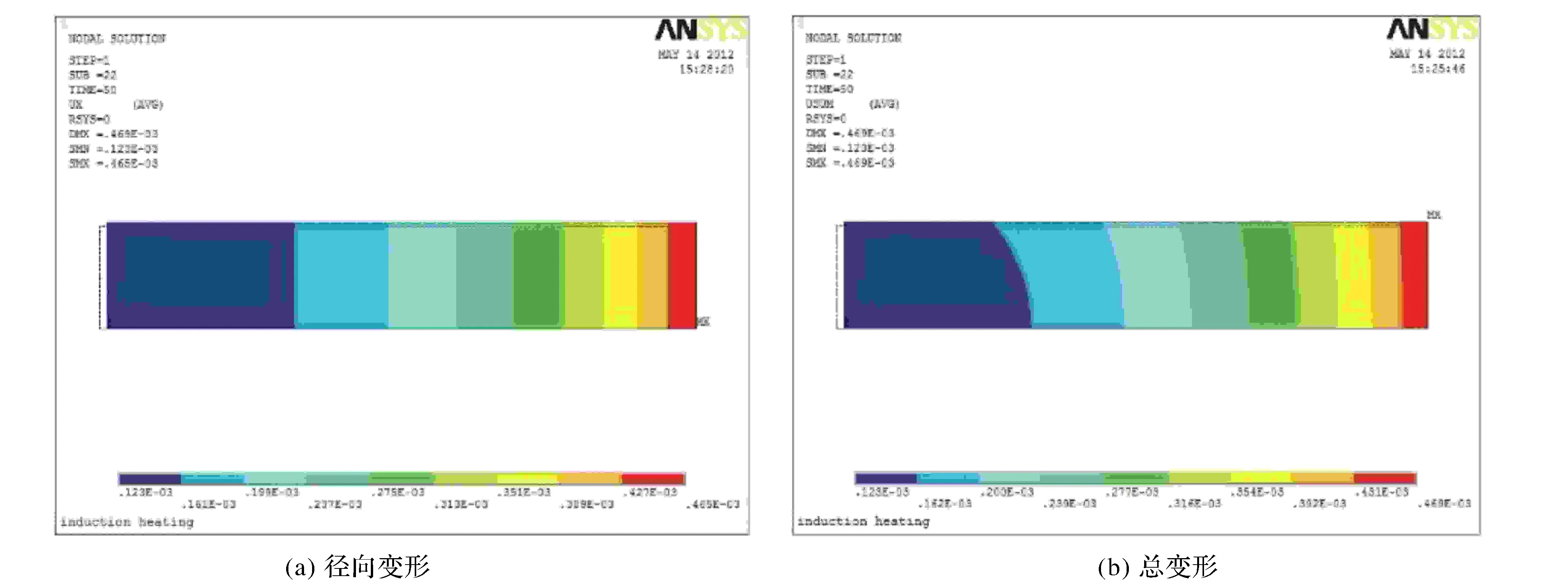
图6 热变形等值线图Fig.6 Contour map of thermal defamation

图7 应力分布等值线图Fig.7 Contour map of stress distribution

表1 砂轮基体内外圈的温度、热应力计算结果Table 1 The values of temperatures and thermal-stress of outer and inner rings of the wheel matrix

总结

本文通过ANSYS有限元仿真方法,分析了高频感应加热钎焊金刚石砂轮时,砂轮基体表面的温度分布状况以及热应力分布和热变形情况。随着加热时间增加,基体外圆温度升高趋缓,内孔表面温度升高速率增加。加热功率越高,基体外表圆表温升越快,基体内外表面的温度差也越大。热应力分析结果砂轮外圈的应力最大,内圈的应力约为外圈应力的一半。在拉应力的作用下,砂轮基体的内孔扩大。砂轮受热变形,基体外圈的变形量最大,内圈的变形量最小。同一圆周半径处,上表面的变形量比下表面的稍大。由于受热膨胀,砂轮基体的厚度稍稍有所增加。

[1] 徐正亚.高频感应钎焊金刚石砂轮的基础研究[D].南京:南京航空航天大学,2008.

[2] A.K.Chattopadhyay,H.E.Hintermann.New generation super abrasive tool with monolayer configuration[J].Diamond and Related Materials,1992,1:1131-1143.

[3] 傅玉灿,徐鸿钧.一种适于国内外引进开发的新型糙硬磨料砂轮——国外单层钎焊糙硬磨料砂轮制造技术评述[J].中国机械工程,1999,10(4):375-377.

[4] 卢金斌.金刚石钎焊机理与工艺基础研究[D].南京:南京航空航天大学,2004.

[5] 张凤林.Cr、Ti金属粉改善Ag-Cu-Zn合金对金刚石的钎焊性能研究[J].金刚石与磨料磨具工程,2007,3(159):22-25.

[6] 姜建华.厚壁筒形坯料连续感应加热处理有限元模拟[J].材料热处理学报,2002,23(2):43-48.

[7] 党沙沙,许洋,张红松,等.ANSYS 12.0多物理耦合场有限元分析从热门到精通[M].北京:机械工业出版社,2010.

[8] 约翰.戴维斯[英]著.感应加热手册[M].张淑芳译.北京:国防工业出版社,1985.

Analysis of the Change of Temperature Field of Brazing Diamond Grinding Wheel Matrix During the Induction Heating Process

ZHANG Mei-qin1,WU Hai-rong2
(1.School of Mechanical and Automotive,Xiamen University of Technology,Xiamen,Fujian,China 361021; 2.Institution of Manufacture Engineering,Huaqiao University,Xiamen,Fujian,China361021)

Distribution regularity of the temperature field of brazing diamond grinding wheel matrix during the high frequency induction heating process has been analyzed through finite element analysis.The regularity of temperature distribution of wheel matrix changing with heating time,heating power and position has been analyzed through simplified model of the induction heating and magneto-thermal coupled analysis.Result shows that the temperature of the wheel matrix increases rapidly when heated;the heating rate becomes higher as the heating power gets higher,and bigger temperature difference between matrix inner hole and cylindrical surface has been produced.This difference becomes bigger as time progresses.The stress of the outer ring of the grinding wheel is twice as much as that of the inner ring.The outer ring has maximum thermal deformation while the inner ring has minimum thermal deformation.The inner hole of the grinding wheel expands under heat stress conditions.

brazing;diamond;grinding wheel;induction heating;temperature;finite element analysis

TQ164

A

1673-1433(2015)06-0022-05

2015-10-10

张美琴(1983-),女,硕士,实验师。E-mail:mqzhang@xmut.edu.cn。

福建省厦门市科技计划指导性项目(3502Z20077003);福建省教育厅A类科技项目(JA13019)

张美琴(1983-),女,硕士,实验师。Email:mqzhang@xmut.edu.cn

张美琴,吴海融.感应加热钎焊金刚石砂轮过程基体温度场变化分析[J].超硬材料工程,2015,27(6):1-5.