轮毂轴承径向迷宫密封齿型角的数值研究

雷贤卿，牛屾，郭长建

（1.河南科技大学 机电工程学院，河南 洛阳 471003；2.人本集团 技术中心，上海 201411）

轮毂轴承是汽车重要的零部件，其主要作用是承载，精确引导轮毂的转动。轮毂轴承的密封性差会导致其内部润滑脂的泄漏和外部泥沙、水汽、灰尘等污染物的侵入，不仅影响轴承的使用寿命，甚至会造成严重的交通事故。因此，对轮毂轴承的密封性有非常严格的要求。

为改善轮毂轴承的密封性，国内外一些专家学者进行了相关研究。文献［1］对轮毂轴承的密封唇采用了大U形结构和主副密封唇结构；文献［2］设计了轴向和径向双唇口互补接触式密封；文献［3］为双列汽车轮毂轴承开发了低摩擦整体式密封。虽然这些研究在一定程度上提高了轴承的密封效果，但大多是生产厂家靠经验或者对某一轴承在某一工况下的多唇接触式密封结构的改进，没有分析轴承漏脂的根本原因，而且参数确定的理论依据也不够充分。

1 轮毂轴承迷宫密封简化模型

密封轴承漏脂的根本原因是轴承运转引起的内部润滑脂的重新分布以及内部空气的温升［4］，高温导致了气压增加，推动密封唇向外扩张，使得润滑脂被挤出，造成了漏脂现象。因此，仅仅依靠改进多唇接触式密封结构并不能从根本上解决轮毂轴承单元的漏脂问题，需要选用能够转化、衰减内部气压聚集的密封结构。

迷宫密封具有摩擦小、寿命长的优点，适用于中高速场合。气流在迷宫密封中通过节流齿隙的节流作用和迷宫空腔的能量耗散达到密封的效果［5］。由于轮毂轴承的轴向尺寸紧凑、径向尺寸较大，因此，径向迷宫密封结构比较适合汽车轮毂轴承。由于该结构本身具有的功能优势，可将其作为研究新型低摩擦力矩密封结构的一个方向［6］。

迷宫密封齿型角是影响迷宫密封结构的重要参数，增大齿型角可以增加密封齿根部的宽度，有利于提高密封圈的强度，但对迷宫密封的性能也会产生很大的影响。目前，对轮毂轴承径向迷宫密封结构最佳齿型角的研究较少。下文以某汽车轮毂轴承单元径向直通式迷宫密封结构为研究对象，应用ANSYSFLUENT软件平台，结合计算流体力学相关理论，研究不同压比下齿型角对泄漏量的影响规律。迷宫密封结构如图1所示，图中θ为齿型角。

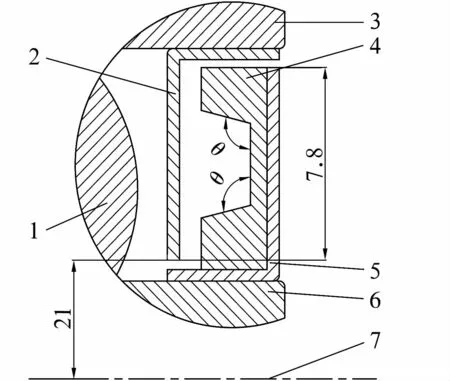
图1 轮毂轴承径向直通式迷宫密封结构

2 流体计算模型和收敛标准

流体在迷宫密封内的流动过程可以认为是二维稳态标准湍流流动［7］。流体在迷宫密封中的流动采用Reynolds平均Navier-Stokes方程和k-ε湍流模型来描述，其中包括连续性方程、能量方程、湍动能方程、动量方程和耗散率方程［8］。使用散度符号可得方程的通用形式

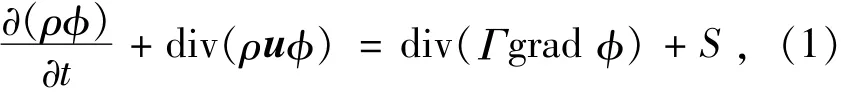
式中：ρ为流体密度；t为时间；ϕ为通用变量；u为流体速度矢量；Γ为广义扩散系数；S为广义源项。

对（1）式的离散采用有限体积法，为保证计算精度，连续性方程、能量方程和动量方程的离散采用二阶迎风格式，湍动能方程和耗散率方程采用一阶迎风格式，压力插值格式采用标准插值。当连续性方程、速度、湍动能及湍动能耗散率的残差都小于1×10-4，能量方程的残差小于1×10-6，进出口流量相差小于0.1%时，可认为计算收敛［9］。

3 边界条件

采用ANSYSFLUENT软件对迷宫密封二维流场进行仿真计算，边界条件设置为：迷宫密封左端采用压力入口，模拟工作总压分别为0.15，0.21，0.27和0.35 MPa，气流方向垂直于入口边界；右端出口压力为大气压，其值为0.1 MPa。轴承模拟内圈工作转速为3 000 r／min，其中芯轴即为迷宫密封模型的旋转轴。轴承内外圈相对运动采用移动参考系模型（MRF）模拟，并将参考坐标系设置在流场区域，边界壁面均采用无滑移无渗透的固体壁面。求解器采用SIMPLE算法。工作介质采用理想气体。计算收敛后，用测得迷宫密封压力出口的质量流速来表示理想气体的仿真泄漏量。仿真泄漏量越小说明轮毂轴承内部聚集的气压势能在迷宫密封内转化、衰减得越充分，密封性能就越好。

4 数值计算与仿真

4.1 几何模型

该轮毂轴承单元径向迷宫密封流场的几何模型如图2所示，几何参数：总长L＝7.8 mm；密封齿高H＝2.5 mm；齿宽M＝2.4 mm；腔室顶端宽度W＝3 mm；间隙宽C＝0.2 mm。齿型角θ为变量，分别取90°，94.5°，99°，103.5°和108°。

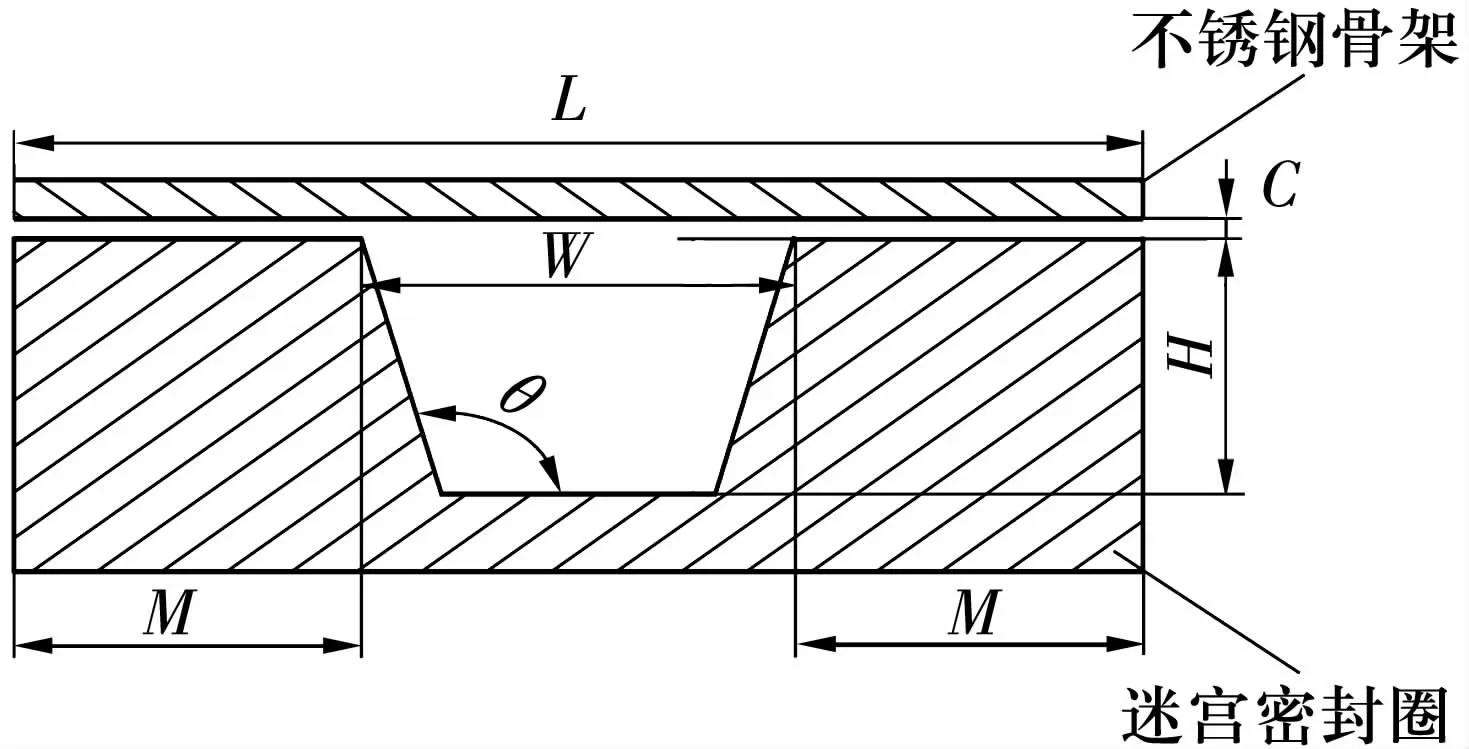
图2 轮毂轴承径向迷宫密封流场的几何模型

4.2 网格划分

采用ANSYS ICEM CFD前处理软件导入几何模型并生成的二维四边形结构化网格如图3所示。为了保证计算精度，最大网格尺寸为0.01 mm，并对流动比较复杂的近壁面处进行网格加密处理［10］。

图3 二维结构化网格划分

4.3 仿真结果

泄漏量随齿型角的变化规律如图4所示。由图可知，4种压比下泄漏量的变化规律基本一致。在所设定的结构尺寸下，随着齿型角的增加，空腔形状由矩形变为等腰梯形，空腔容积逐渐减小，泄漏量呈现出先减小后增大的变化规律。当压比增大时，最佳齿型角（泄漏量最小值对应的齿型角）有所减小。因此，当其他结构尺寸一定时，存在最佳齿型角使得轴承径向迷宫的密封效果最好。

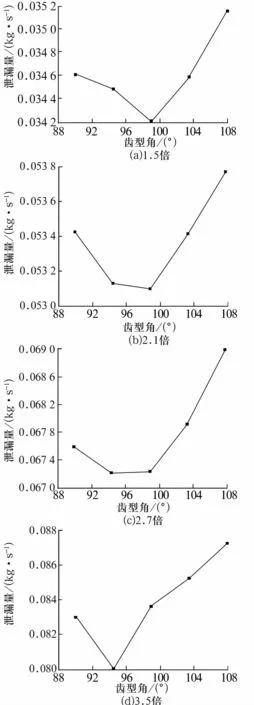
图4 不同压比下泄漏量随齿型角的变化规律

4.4 密封机理分析

在2.1倍压比下，齿型角为99°时轴承迷宫密封流场的仿真压力和速度分布云图如图5所示。

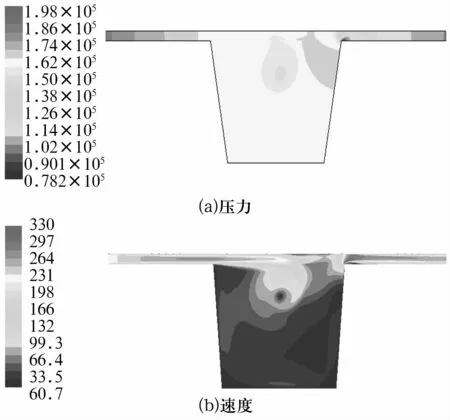
图5 齿型角为99°的密封流场在2.1倍压比下压力和速度分布云图

由图5可知，在压差推动下，气流从左端入口高压侧向右端出口低压侧流动。当气流进入密封间隙时，由于流道变窄，流速增高，压力降低，即压力势能转化为动能；当气流进入空腔时，由于流动截面面积突然增大，从间隙出来形成高速射流的气体，和空腔内部低速湍流的气体之间不断发生摩擦和掺混，产生了剧烈的绕流漩涡，使得气体大部分动能转化为热能，从而达到迷宫密封的效果。

在2.1倍压比下，齿型角分别为90°，94.5°，103.5°和108°时轴承迷宫密封流场的速度分布如图6所示。

对比图5和图6可知，气流经密封间隙流出后，形成强烈的射流冲击到密封空腔中，并且呈一定角度扩散，与壁面和周围介质发生摩擦和掺混，形成一个主涡。当齿型角为90°时，主涡在空腔中部偏左的位置，空腔右下方大部分气流速度较低，几乎静止。随着齿型角的增大，不仅主涡的位置逐渐右移，而且空腔左右下角原先大量静止的气体也开始运动。当齿型角为99°时，主涡在空腔中部，空腔左右下角原先几乎静止的气体不断与主涡周围形成的气流发生摩擦和掺混，并形成了几个小涡，空腔内气体参与能量转换较为充分，此时泄漏量较小。当齿型角继续增大时，空腔容积继续减小，主涡逐渐偏向压力出口，空腔右侧气流速度逐渐增高，使大量气体高速流出，导致泄漏量又增大。

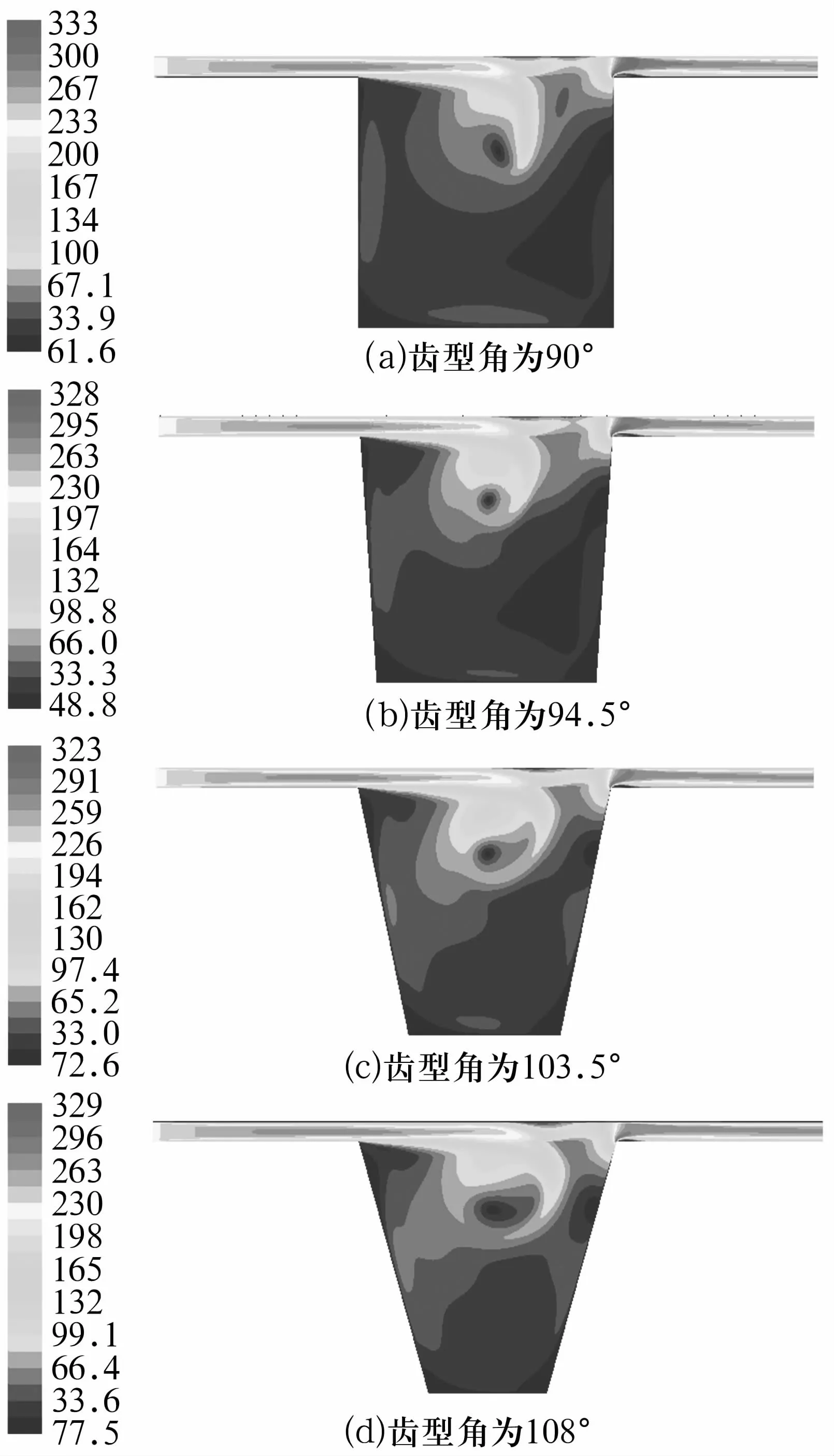
图6 不同齿型角下密封流场的速度分布云图

5 结束语

齿型角的变化对轮毂轴承径向迷宫密封的泄漏量有一定影响，当其他结构尺寸一定，在同一压比下，随着齿型角的增大，迷宫密封的泄漏量先减小后增大。当压比增大时，最佳齿型角减小。对轮毂轴承径向迷宫密封而言，存在最佳齿型角使其泄漏量最小。