轴承套圈超高速离心磨削预应力分析

刘晓初，何铨鹏，代东波，陈凡，郭莹莹

(1．广州大学 机械与电气工程学院，广州 510006；2．广州大学 金属材料强化研磨高性能加工重点实验室，广州 510006)

1 概述

轴承套圈(以下简称工件)的一般加工工艺为：毛坯成形→车削→软磨精整→热处理→磨削→滚道面超精研磨。其中，磨削加工、滚动面超精研加工是轴承生产过程中的关键工序，其质量直接决定轴承的精度、动态性能及可靠性。在磨削过程中，由于磨削热而在工件表面产生的变质层(拉应力层)可使滚道表层硬度下降，且易产生微裂纹，从而降低轴承的疲劳强度。因此，若能在磨削过程中直接控制某些因素，使工件表面层形成残余压应力，将大幅提高轴承的使用寿命。

超高速离心磨削是一种对工件施以高速旋转而带来离心效应和陀螺效应以及周向预应力的新型加工方法。该方法能加工出高精度的、表层具有残余压应力的轴承套圈[1]。

电磁无心夹具具有重复定位精度高、可大幅减小电主轴圆跳动对工件加工精度的影响等优点[2]，所以可采用以工件外圆定位的多磁极式电磁无心夹具来实现超高速磨削的“离心”效果。

文献[3]对硬态切削技术进行了理论研究，结果表明，若加工前预先给工件施加一个弹性范围内的拉应力，加工过程中工件表面会产生塑性变形，加工后将该应力释放，加工表面由于基体的弹性恢复会产生残余压应力，且残余应力与预应力之间成正比关系。

综上所述，超高速离心磨削过程中产生的预应力是影响工件表层残余应力分布状态的主要因素，利用空间应力求解法推导工件预应力表达式，并考察周向应力和轴向应力在工件表面的分布状态，为最终实现残余应力的可控性提供理论基础。

2 磁吸力分析

由电磁原理可知，线圈通电产生磁场，磁场中的磁感线依次通过铁磁芯、磁盘、磁极、支承、支承座、气隙和夹具体后回到铁磁芯，形成一个封闭磁路，从而产生磁吸力[4]。

由于螺管式线圈结构的磁路有气隙，很难准确计算磁吸力，所以引入近似的磁吸力计算公式[5]

(1)

式中：μ0为真空磁导率；B为磁感应强度；S为磁通量横截面面积。

在进行磁力分析时，S一般为常数；μ0为常量，取4π×10-7H/m，因此B是影响Q的主要因素。B的计算式为

(2)

式中：μ为磁导率；H为磁场强度；N为线圈匝数；I为线圈电流；L为磁路的平均长度。

将(2)式代入(1)式得到磁吸力的最终表达式为

(3)

3 工件预应力计算

一方面，由圣维南定理可知，当一个平衡力系作用在物体的某一小部分上，则该平衡力系在物体内所产生的应力分布仅局限于该力系作用区域的附近，在离该区域相当远处会急剧地减小[6-7]，根据电磁无心夹具的工作原理，即使工件与支承之间存在一个平衡力系，但该力系所产生的应力分布只局限于两者接触面的附近，在磨削区域中几乎没有应力产生，所以计算工件预应力时只需考虑磁极对工件的影响；另一方面，在磁极磁场作用下，工件所受磁力与宽度存在函数关系，但实际生产中工件宽度一般较小，且与磁极距离较短，为了简化计算，将工件受到的磁力视为常量，大小与磁极的磁吸力Q相等。此外，考虑到工件内外半径是其宽度的2～5倍，应按空间应力问题求解。

如图1所示，以工件某一表面为基准面，其中心为原点O，建立空间圆柱坐标系，则工件任一点M的圆柱坐标(r,θ,z)和直角坐标(x,y,z)之间的关系分别为x=rcosθ，y=rsinθ，z=z，并规定沿坐标轴r，θ，z方向的物理量分别以下标r，θ，z表示，若物理量有2个下标，则第1个下标表示物理量的作用面，第2个下标表示物理量的方向。

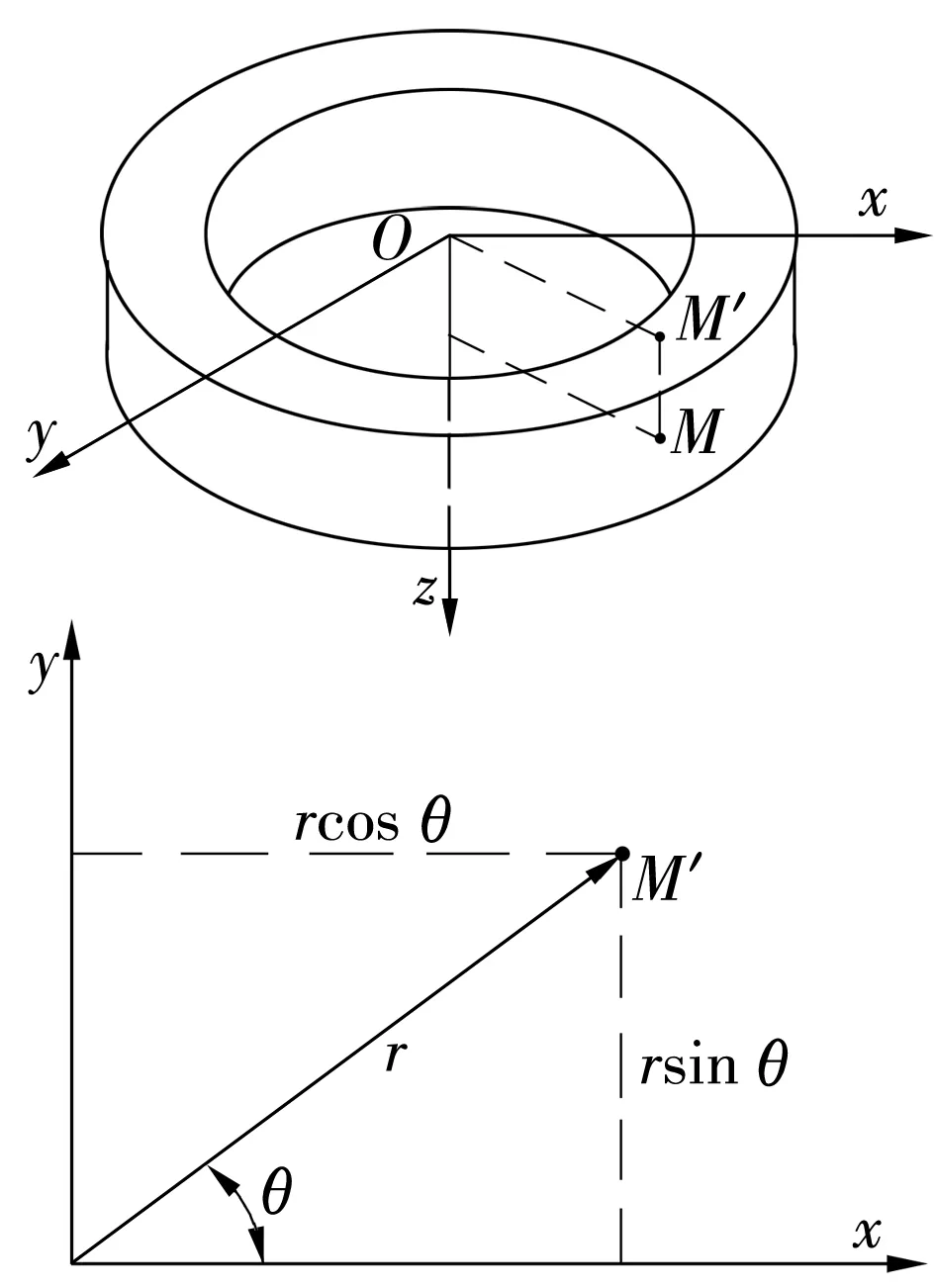
图1 空间坐标下的工件

为简化运算过程，在不计重力作用下将工件受到磁极端面的支持力定义在z=0的平面上，即该表面沿z轴方向的位移量为0，并把惯性力(F=ρω2r)和磁吸力Q作为体积力，已知工件密度为ρ，内圈半径为r0，外圈半径为r1，宽度为B，求工件以角速度ω匀速转动状态下的应力。

通过导出圆柱坐标系形式的基本方程来求解上述弹性力学空间问题，其中包括6个几何方程、3个平衡方程、6个胡克定律下的应力方程[7-8]

(4)

(5)

(6)

ϑ=εr+εθ+εz，

式中：u为位移量；ε为应变量；γ为切应变；σ为正应力；τ为切应力；f为体积力；λ为拉梅系数；G为剪切弹性模量；ϑ为应变张量的第一不变量。

由于工件的几何形状、约束和所受外力均对称于z轴，根据变形对称性，必有uθ=0，γrθ=γzθ=0，τrθ=τzθ=0，其余的位移、应变和应力都与θ角无关[7]。因此在进行轴对称问题求解时，可将(4)～(6)式简化为

(7)

(8)

(9)

将(7)式代入(9)式，然后再代入(8)式，可得平衡方程

(10)

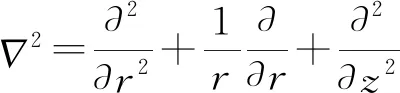
(11)

(11)式的一般解为齐次方程的通解加上一个特解，导出该方程组通解为

为简化计算，设ur=D1rk1，uz=D2zk2，代入(11)式求出其特解为

因此，(11)式的一般解为

(12)

将(12)式代入(7)式导出应变表达式

(13)

再将(13)式代入(9)式可导出应力表达式为

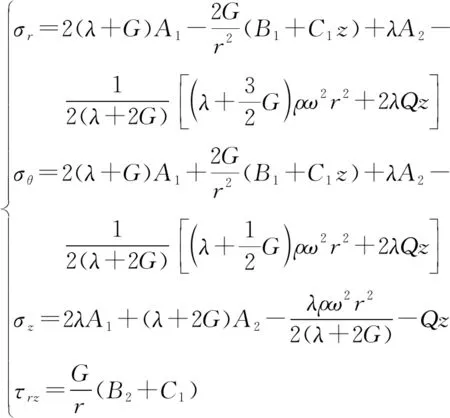
(14)

(12)～(14)式共10个方程，包含5个未知量，所以本问题的边界条件至少有5个，分别为

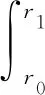
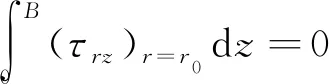
因此，工件高速旋转状态下的应力表达式为

(15)

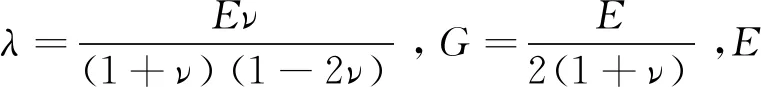
(16)

由(16)式可知，当r，z和Q为定值时，σr，σθ，σz均与ω2成正比，即工件转速越高，所产生的预应力越大。大量实践表明，当周向预应力为拉应力时，加工后工件表面可获得残余压应力，反之则为残余拉应力[9]。经分析，利用超高速离心磨削方法来延长轴承套圈的使用寿命，其本质是通过预应力磨削使工件表面获得良好的残余压应力，轴向预应力σz即使为压应力，但相对周向预应力σθ(拉应力)而言，影响较小。因此，为了进一步说明周向应力和轴向应力的影响程度，需考察二者在工件表面上的分布情况。

4 实例分析

以飞机发动机主轴中用角接触球轴承内圈(QJ1019)磨削为例，套圈相关参数见表1。

表1 QJ1019轴承内圈参数

在考察周向应力和轴向应力的分布时，自变量为nw(r/min)和z(mm)，具体步骤为：

1) 确定自变量的考察范围；

2) 估算出磁吸力Q；

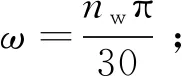
4)根据(15)式导出σθ和σz的具体计算公式；

5)由计算公式，利用MATLAB绘制出相应的应力分布图。

在确定自变量范围时，取nw∈[104，3×104]r/min，z∈[0，24]mm。工件转速大幅度提高，将破坏传统磨削工艺中工件与砂轮转速之间的比例关系，还可能带来其他负面影响，如工件与支承之间滑动速度过高使工件表面形成支点印；离心力过大使工件从支承上飞出等。因此，需通过变速磨削、合理调整电磁无心夹具的几何参数(偏心象限、偏心量、支承角等)、提高套圈与支承间的冷却和润滑效果、以浮动支承来代替固定支承等方法避免上述问题的发生。

在估算磁吸力Q时，μ=μ0μr，通过查阅电工手册[5,10]可知，铸铁的相对磁导率μr为200～400，取μr=300，则μ=300×4π×10-7=3.8×10-4H/m；根据电磁无心夹具结构估算L=0.2 m；在电磁无心夹具的设计中n为1 000～2 500，则取n=2 000；线圈材料一般为铜丝，其电流密度J=2～4 A/mm2，假设铜丝直径为0.5 mm，其横截面积A为0.196 3 mm2，则I=JA=0.39～0.79 A，取I=0.6 A；根据工件尺寸估算S≈3.074×10-3m2。将上述数据代入(3)式估算出磁吸力Q≈6 360 N，方向与z轴相反。

令r=r1，将Q≈6 360 N以及表1中参数代入(15)式，分别导出σθ和σz的具体计算公式

(17)

根据(16)式和自变量取值范围，利用MATLAB绘制σθ和σz的应力分布如图2所示。

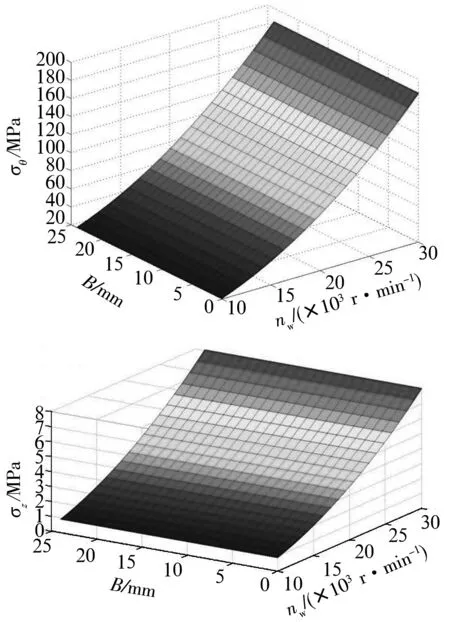
图2 σθ和σz应力分布

由图2可知，工件高速旋转状态下，其表面的周向预应力为拉应力，而轴向预应力为压应力；在σθ和σz的应力曲面上，沿宽度方向的曲线曲率较小，即工件表面的应力分布基本不受磁吸力Q的影响。

令z=12 mm，分别得出周向应力和轴向应力与工件转速的关系曲线，如图3所示。比较二者数值大小，σθ至少是σz的20倍，即磨削过程中工件表面的周向预应力(拉应力)对残余压应力的形成起主导作用。

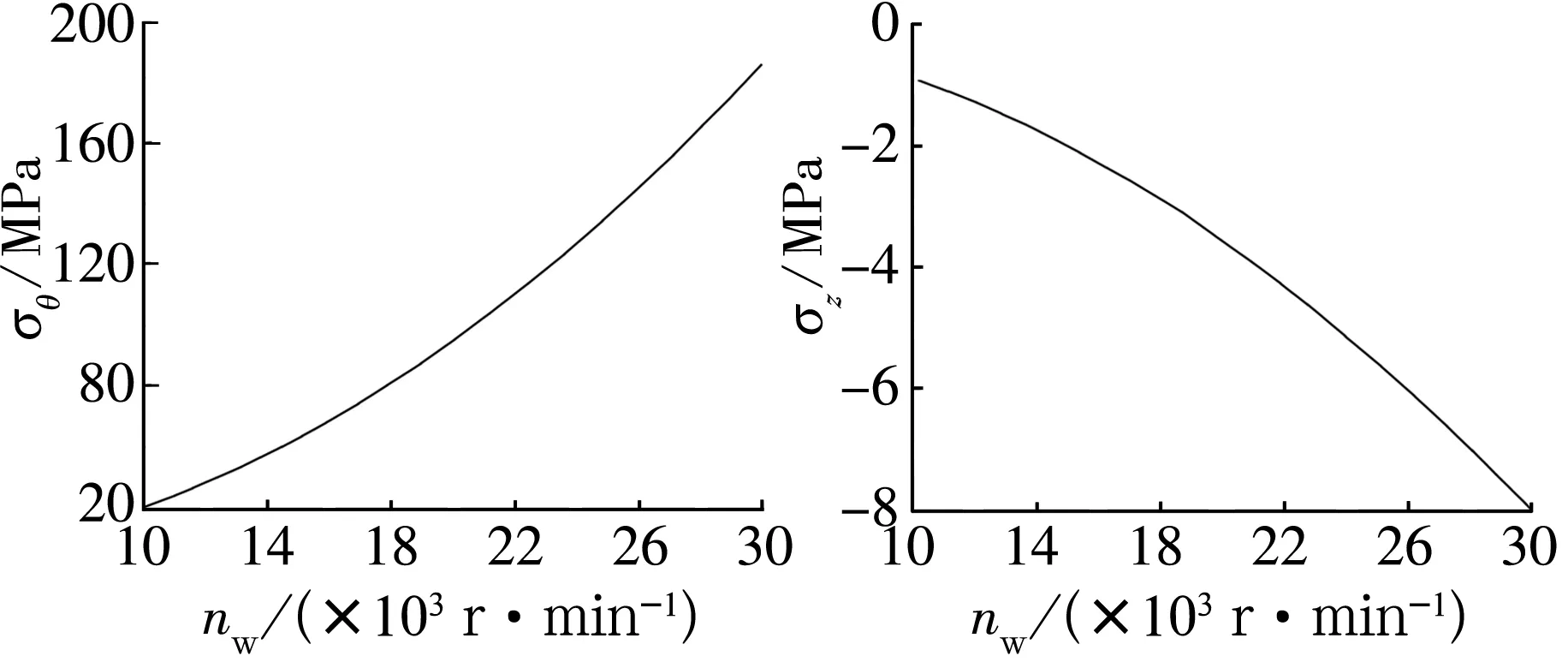
图3 当z=12 mm时，σθ，σz与nw的关系

假设高速旋转下的工件可自由膨胀，利用平面法导出其应力表达式为

(18)

图4 空间法与平面法比较

5 结论

1)由预应力表达式可知，当r,z和Q为定值时，σr，σθ，σz均与ω2成正比，即角速度越大，预应力越大。

2)工件表面的周向预应力(拉应力)至少是轴向预应力(压应力)的20倍，所以提高工件转速有利于工件表面残余压应力的形成。

3)在分析工件表面周向预应力的问题上，分别利用空间法和平面法进行求解，二者误差小于2%。