自然河道一维水流数学模型
2015-07-25健夏春晨王建刚梁建秀王
王 健夏春晨王建刚梁建秀王 姣
(1.山西省汾河中下游水务管理局 山西太原 030002;2.武汉大学水利水电学院 湖北武汉430072;3.太原市水利勘测设计院 山西太原 030002)
0 引言
在工程实践中,常常要用非恒定流的原理对河道、水库或渠道等水流进行计算,以掌握其水面线和流量等数据,为工程设计、洪水预报、水库调度、溃坝洪水演进计算等提供科学依据和计算基础[1]。在实际情况中,对一些简单的工程,可以利用恒定流计算,但有时仅靠这些计算往往不能反映实际情况,如山区河流等河道地形变化复杂时,水流非恒定,可能会出现急流、缓流、临界流交替的急变情况,此时适用于渐变流的传统恒定非均匀水流数学模型可能无法满足工程需要。
为解决这一问题,需要利用理论严谨、计算精度较高的非恒定流原理。本文基于完整的圣维南方程,开发了自然河道一维水流数学模型,采用有限体积的思想[2-3],利用SLIC(Slope Limiter Centred Scheme)数值格式[4]来计算自然河道的水面线及其他水力要素。该数值方法不仅适用于恒定或非恒定流,均匀或非均匀流,而且可以计算跨临界流的急缓流交替的急变情况,能够在实际中得到较为广泛的运用。
1 自然河道一维水流数学模型
1.1 控制方程
天然河道断面通常呈现为具有滩地和主槽的复式断面,如图1所示。传统方法求解自然河道断面阻力时,将断面分割成独立的几个子断面分别求解,这很显然忽略了各子断面之间的动量交换作用,因此,这样得到的综合糙率是存在一定误差的。本文基于完整的一维圣维南方程组,利用最新发展的断面综合糙率和动量通量计算模式[5],建立河道一维水流数学模型,为河流工程实践提供技术基础。
假定水的密度不变并且没有横向入流的情况下,一维圣维南方程组如下:

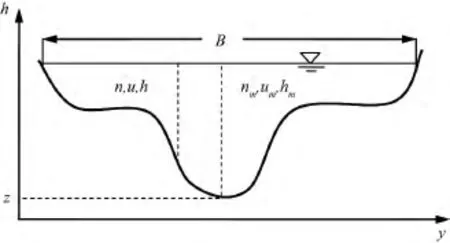
图1 自然河道断面示意图
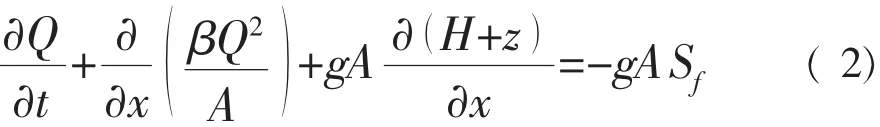
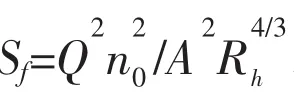
按照最近提出的计算模式,河道断面动量修正系数和综合糙率表达式

其中:y为河宽方向;P为湿周,其他系数表示如下:
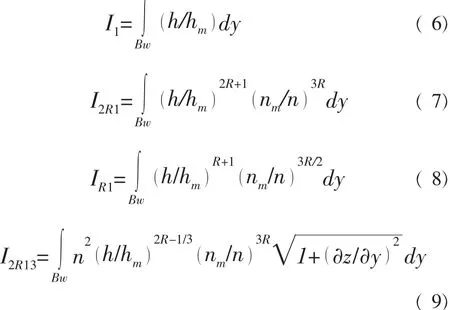
其中:h为当地水深;n为当地糙率;hm为参考点水深,一般取为断面最大水深;nm为参考点糙率;R为待定参数,与滩地类型有关:
对于光滑滩地:R=0.7987-1.1955Dr+0.5138(10)
对于粗糙滩地:R=-1.799+0.0885Dr+0.5704(11)
其中:Dr=(H-hmc)/H为滩地相对水深;hmc为主槽水深。
1.2 数值格式
将式(1)、(2)写成守恒型方程组:

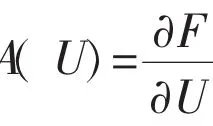

雅格比矩阵A(U)有两个特征值:

将式(12)进行离散

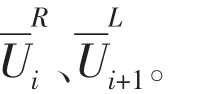


为了使计算稳定,时间步长需要满足科朗条件:

即科朗数Cr<1,λmax为由雅格比矩阵求得的最大特征值。
该数值格式方法基于有限体积的思想,能够捕捉到激波,解决在部分河段出现急变流的情况,同时也适用于求解渐变流问题。
2 算例分析
2.1 非恒定流水力计算
对一断面形态如图1的自然河道[5],总长为100 km,其中主槽深hmc=5 m;河底宽b=20 m,水面宽B=400 m;左右滩地宽bl=br=175 m;滩地及主槽边坡Sfp=Smc=3.0;滩地及主槽糙率nfp=nmc=0.03;河道底坡Sb=0.000 2;x=0 m时水位z=4 m。对于非恒定流,上游来流为对数皮尔逊Ⅲ流量过程如图2,初始流量为Q0=120 m3/s,在t=900 min时达到峰值流量Qmax=1200m3/s。下游为给定的水位流量关系,如式(24)所示,其中Hn为初始下游水位,Hn=4.5 m。初始各断面为恒定流状态下的水深。

图2 上游流量过程线
对于圣维南方程式(1)-(2),定义修正圣维南方程的 β、n0通过式(3)-(4)进行计算,传统圣维南方程通过β≈1,n0=0.03计算,结合SLIC数值格式计算并比较两者在上述条件下代表断面的水位随时间变化情况,如图3所示。本文采用的数值计算格式与曹志先教授[5]不同,但计算结果相一致。
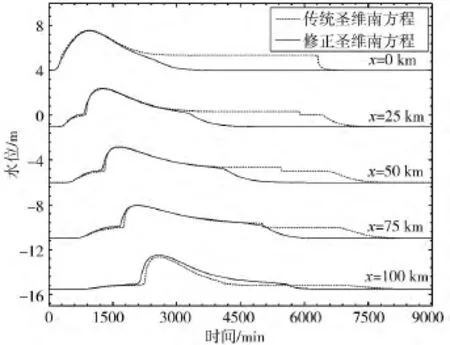
图3 代表断面水位过程比较图
当流量逐渐增大,水流刚刚漫滩时,水面突然展宽,湿周、水力半径等水力要素均会发生突变,导致流速突然减小。从图3中可以看出当滩地水深很小,利用传统圣维南方程求解会带来计算问题[6],在退水过程中表现较为明显,出现了水位不连续的现象,而基于修正的圣维南方程的计算结果则较为理想的改善了这一情况。这体现了利用修正圣维南方程进行自然河道水力计算的优越性。
2.2 涑水河段水力计算
涑水河流域发源于绛县的陈村峪,河流总长为195 km。流域范围包括闻喜县、夏县、盐湖区、临猗县、永济市的绝大部分和绛县、万荣县的一部分。根据河道特性可将涑水河分为四个河段:吕庄水库以上河段长54 km,河型为“V”字形,纵坡1/70。吕庄水库至上马水库段长41km,为复式断面,复槽最宽处达1600m,主槽10~20 m,纵坡1/700;上马水库至伍姓湖段长64 km,为人工开挖,窄深式,纵坡为1/850;伍姓湖至入黄口段长37 km,纵坡为1/4 000,河床比较稳定。
研究河段为陈村峪~杨家园水库河段,该河段位于涑水河上游,其中有紫家峪和冷口峪支流汇入,因此将该研究河段分为三个小河段分别进行计算。
根据《山西省运城市涑水河重点河道治理工程初步设计报告(陈村峪~伍姓湖入口)》和《山西省运城市涑水河重点河道治理工程初步设计图纸(陈村峪~上马水库)》得到计算河段设计洪峰流量成果表,如表1所示。同时分析以下三种情况:设计情况,在设计洪峰流量条件下,在设计图纸中标注的设计河床高程以及设计水位数据;计算情况(修正法),在设计洪峰流量条件下,河床高程数据同设计情况,但未获得计算河段准确的断面数据,因此采用从纸质的设计图纸中量取的断面形态数据,采用修正的圣维南方程和SLIC数值格式计算水位;计算情况(传统法),除糙率采用传统综合糙率法计算外,其它同计算情况(修正法)。

表1 陈村峪~杨家园水库各区间设计洪峰流量成果表(P=5%)
首先,采用设计情况的数据进行复核,该河段的佛氏数图如图4所示。从图中可以看出,在陈村峪~杨家园水库上游河段的佛氏数大于1、等于1和小于1的情况均有出现,说明出现了急流或者急缓流交替的急变情况,在这样的情况下,仅适用于渐变流假设条件下的恒定非均匀流数值模型理论显然存在缺陷。因此需采用本文提出的基于完整的一维圣维南方程并结合SLIC数值计算格式求解该河段的水面曲线。
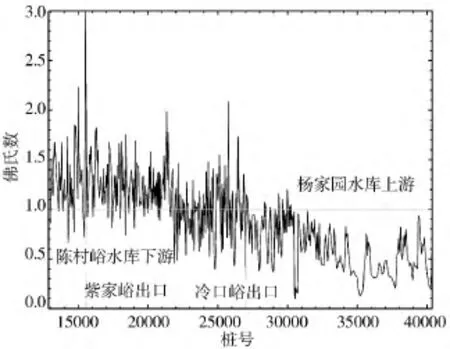
图4 陈村峪~杨家园水库河段佛氏数图

图5 陈村峪~杨家园水库河段水深图

图6 陈村峪~杨家园水库河段水位图

图7 陈村峪~杨家园水库河段传统法与修正法水深比较图
在设计情况和计算情况(修正法)下的水深、水位结果如图5、图6所示。从图中可以看出,设计水位与计算水位的趋势相对一致,但是个别断面差距较大,水深差值最大值出现在桩号为30+000前后的河床陡坎处,地形发生较大的突变。同时,考察计算情况(修正法)和计算情况(传统法)下的水深结果,如图7所示,两者计算结果差异非常小,在该计算河段中综合糙率估算方法对水深差异的影响几乎可以忽略。因此,引起水深差异主要原因一方面来自水力学数值模型的差异,另一方面还有地形的影响,由于无法获得计算河段准确的断面数据,只能利用纸质设计图纸中量取估计的断面形态数据进行计算,这使得计算断面与实际设计断面数据存在了较大差异。
由于涑水河上游出现跨临界流的急变流情况,利用经过修正一维圣维南方程,并采用SLIC数值格式求解水力要素,解决涑水河上游河段出现跨临界流的急缓流交替情况下的水力计算问题,将最新的现代计算水力学理论运用于实际工程计算中,体现了其优越性和先进性。
3 结论
在实际河道工程计算中,往往需要对水流流态进行判断,当水流中出现急流、缓流、临界流共存急变流情况下,传统恒定非均匀水流数学模型的适用性就值得商榷。本文基于完整的圣维南方程和有限体积数值计算格式,开发了自然河道一维水流数学模型,可广泛适用于恒定或非恒定、均匀或非均匀以及急流、缓流和临界流共存的河流之水力计算。对涑水河的实例(数值模拟)研究显示了其适用性与优越性。
[1]刘 洋.几种水面线推算方法的比较[J].人民黄河,2011,33(2):51-53.
[2]周雪漪.计算水力学[M].北京:清华大学出版社,1995.
[3]汪德灌.计算水力学理论与应用[M].南京:河海大学出版社,1989.
[4]Toro E F.Shock-capturing methods for free-surface shallow flows[M].England:John Wiley,2001.
[5]Cao Z,Meng J,Pender G and Wallis S.Flow resistance and momentum flux in compound open channels[J].Journal of Hydraulic Engineering,ASCE,2006,132(12):1272-1282.
[6]Cunge J A,Holly F M,Verwey A.Practical aspects of computational river hydraulics[M].London:Pitman,1980.
