漳泽水库泄流计算参数优化分析

任建营张新建任 婕

（1.山西省漳泽水库管理局 山西长治 046021；2.山西省防汛抗旱指挥部办公室 山西太原 030002）

1 缘起

漳泽水库位于山西省长治市北郊，是海河流域漳卫南运河水系浊漳南源干流上的一座以工业、城市供水、防洪、灌溉为主兼顾水产养殖、旅游等综合利用的大（2）型水利工程。流域面积3 176 km2，总库容4.273亿m3。

近十多年来，漳泽水库管理局大力进行水库管理信息化建设，在水库防洪调度和日常兴利调度方面于省内最早开发使用调洪计算软件[1]，该软件中设置了泄水洞和溢洪道闸门开度计算功能，用于水库日常泄水的计算。随着水库管理水平的日益提高，对水库防洪和兴利调度计算精度方面也提出了更高的要求。漳泽水库位于太行山上党盆地，为平原水库，大坝长2 514 m，正常高水位时水面面积31 km2，每厘米的水位差就有几十万立方米库容，原有50 cm的水位数据级差难以满足日益精细管理的需求。

2010年，水库管理局以1 cm级差的水位—库容—面积数据为基础，升级改造水库调洪计算软件。在此过程中，发现并解决了泄水洞闸门流量计算精度偏低和溢洪道孔堰流边界系数精度偏低带来的问题。

2 泄水洞流量计算精度的提高

漳泽水库泄水洞位于大坝坝轴桩号0+800处，为坝内埋管式半有压洞，洞首为高25.5 m的进水塔，内装3.4m×3.7m（宽×高）平板钢闸门，洞身断面为3.2m×3.575 m（宽×高）的马蹄型，设计限制最大下泄流量为90 m3/s。

在水库泄水流量不大时，一般多通过泄水洞泄水。在库水位不同时，同样的泄水流量闸门开度是不同的。根据泄水洞流量计算公式①，已知上游水头H和闸门开度e手工计算求泄水流量Q比较容易，但由于闸门开度e不能变换为以上游水头H和泄水流量Q为自变量的显函数形式，故已知上游水头H和泄水流量Q不能直接求出闸门开度e。以往一般采用试算法或者查曲线图的方法来求解闸门的开度，不仅计算速度慢，精度也不高。因此，开发计算机软件用数值解法解决闸门开度计算的问题非常必要，它既提高了计算精度，又提高了工作效率。

该功能的使用方法是：以人机对话方式输入库水位和泄水流量，选择泄水洞为泄水建筑物后，便可计算出泄水洞闸门开度。由于闸门开度是按泄水开始时的库水位计算的，故不能考虑由于泄水引起库水位下降后，对泄水流量的影响。对于较大流量、较长时间的泄水，应在库水位发生变化后，重新计算闸门开度。

2.1 泄水洞流量计算问题的发现

在闸门开度计算应用实践中，发现计算机软件泄水洞流量计算存在较大误差，例如：上游水头8.7 m时，要求计算下泄流量为15 m3/s，通过软件计算可得闸门开度为0.512 m，如果把闸门开度为0.512 m的计算结果带入到公式①，得出泄水洞流量14.33 m3/s，计算精度为95.53%，误差较大。

式中：Q——泄水洞流量，m3/s；

m——流量系数，无量纲；

b——闸宽，b=3.2 m；

e——闸门开度，m；

H——上游水头，m，H为库水位高程减泄水洞进口底高程后之值；

ε——垂直收缩系数。

我们先是改进计算方法来提高计算精度，但效果不明显。

2.2 问题的解决

在泄水洞流量计算中，m和ε是重要的计算参数，但它们却不是常数，而是随着上游水头H和闸门开度e的比值e/H而变化的量，这种变化规律无法用精确的数学公式表达，只是两个数值表，计算者只能通过插值计算的方法来确定m和ε的取值。表1就是漳泽水库泄水洞原设计提供的ε取值表。

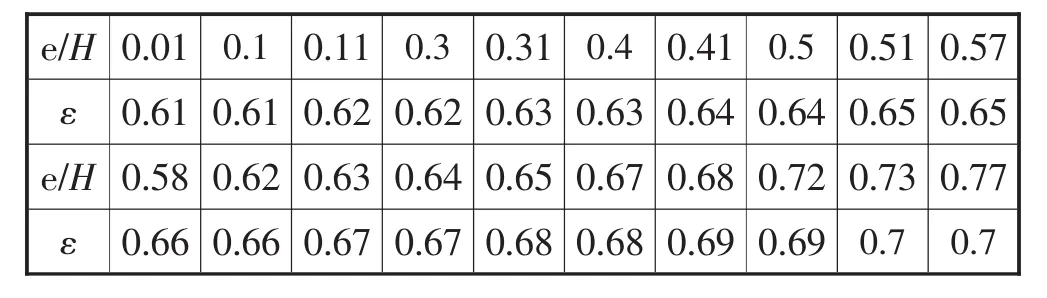
表1 漳泽水库泄水洞设计提供的ε取值表

通过仔细观察发现，原来提供的公式计算参数中闸门垂直收缩系数ε表数值分布不均、精度偏低，小数点后的有效数字只有2位，这有可能是计算精度不高的原因，但一时我们也找不到更高精度的参数表来替代。

后来通过查阅《水力学计算手册》[2]发现了泄水洞流量计算闸门垂直收缩系数参数表，于是采用了以下表2新的ε表格数据。

表2 泄水洞流量计算闸门垂直收缩系数ε参数表

表2比表1的参数分布均匀，闸门垂直收缩系数ε值提高了一个量级。通过闸门开度计算软件测试，采用新的参数后，通过一系列数据测算，泄水洞流量计算精度有所提高，见表3。

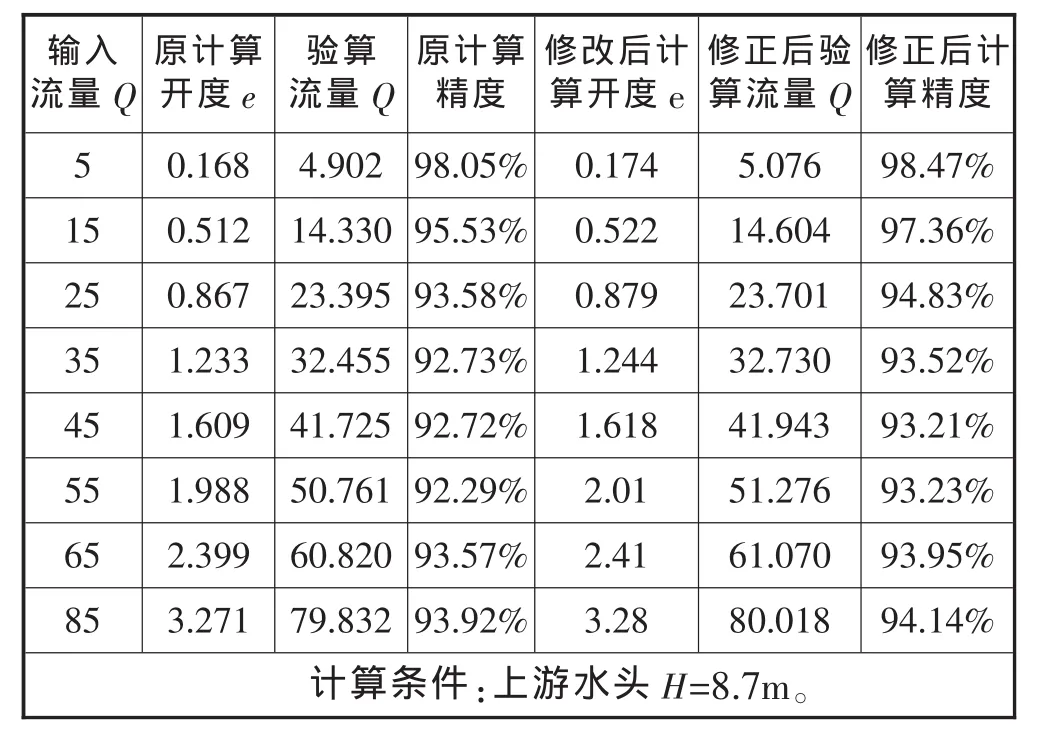
表3 泄水洞闸门垂直收缩系数ε取值变化前后流量计算对比表

3 溢洪道相对开度精度的提高

溢洪道位于大坝右端，为正槽开敞式，闸室设胸墙，设4孔9.2 m×6.6 m（宽×高）的弧形钢闸门，采用2×400 kN的油压启闭机。溢流堰为低驼峰堰，堰前铺盖高程比堰顶高程低2.0 m，胸墙底高程比堰顶高程高6.6 m。闸门高6.6 m，单孔宽9.2 m，4孔全宽36.8 m。出口为挑流消能，溢洪道全长304.0 m，最大流量2 100 m3/s。

3.1 问题的发现

溢洪道流量计算公式如下：

（1）当开度e＜0.7H，为孔口出流，采用公式②

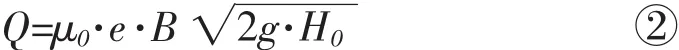
式中：Q——溢洪道流量，m3/s；

μ0——流量系数，μ0=0.685-0.19e/H；

e——闸门开度，m；

B——堰长，B＝9.2×4＝36.8 m；

H0——溢洪道前包括行进流速在内的堰顶水头值，H0=H+（α·υ02）/（2g）,由于溢洪道闸前开阔，流速υ0很小，可忽略不计，即H0=H。

（2）当开度e≥0.7H，为堰流，采用公式③

式中：Q——溢洪道流量，m3/s；

ε——侧收缩系数，ε=0.9；

m——流量系数，当P/H＞0.34时，m=0.452（P/H)-0.032；当P/H≤0.34时，m=0.385+0.224×（P/H)0.934；

B——堰长，B=9.2×4＝36.8 m；

H——堰顶水头，m；

P——堰高，P=2 m。

库水位级差为1 cm计算溢洪道泄流能力时，发现溢洪道在堰顶水头9.43 m处变为孔流，计算流量值比堰顶水头9.42 m时减小32.7 m3/s，出现了在堰流变孔流时两个公式计算结果衔接不好，得到的计算结果见表4。

结合该区间附近的数据，得到以下局部误差放大图。

3.2 问题的解决

在堰顶水头9.4 m附近，正好是两个计算公式的衔接之处，即堰流转变为孔流的转变点。在堰顶水头[9.39，9.47]之间按堰顶水头级差1 cm计算溢洪道泄流能力时，发现在堰顶水头9.43 m处数据发生异常变化，这在原来按堰顶水头水位级差50 cm时是难以发现的。但公式都是依据经典的水力学理论，本身并无问题，只能考虑公式的参数选择是否合适。

表4 水位级差1 cm溢洪道部分泄流能力计算表

图1 修正前溢洪道水位—流量曲线衔接放大图

通过仔细分析研究并反复计算验证，发现原孔堰流变流系数精度低是导致发生错误的原因，在将原来公式②、③中：当开度e≥0.7H改变为：e≥0.721 3H，即相对开度≥0.721 3时，过渡为堰流，此时，将堰流变孔流公式的分界点堰顶水头前移到9.15 m时，得到的计算结果衔接正常，见表5。

表5 修正后的溢洪道部分泄流能力计算表

采取以上的修正计算公式参数的方法，得到了衔接合理的计算结果，但这样的方法必须在理论上找到合理的根据。根据《水力学计算手册》[2]，对于宽顶堰底坎，判别孔堰流相对开度值为e≥0.65H，实用堰底坎，判别孔堰流相对开度值为e≥0.75H。通过对漳泽水库溢洪道的驼峰堰分析，该驼峰堰既不是宽顶堰，又不同于实用堰，而是介于两者之间，即界于[0.65，0.75]之间，取判别孔堰流相对开度值e=0.721 3H是符合实际情况的。而原来判别孔堰流相对开度e=0.7H可以认为是低精度参数，高精度的水位计算必须有高精度的参数与之配套，这样，可依此对原来的溢洪道泄流能力数据做一个精确的修正。

修改参数后的计算结果的图形如图2：

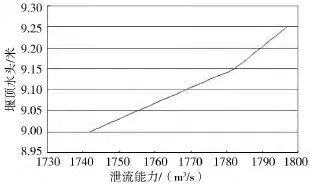
图2 修正后溢洪道堰顶水头—泄流量曲线衔接放大图

4 结论

综上所述，由于计算工具的局限，20世纪中期设计建造的许多水库，其泄水建筑物流量计算公式参数普遍存在精度偏低的情况。在水资源日益紧缺的今天，这种情况已经不能适应水资源精细管理的现实。漳泽水库通过引入新的参数表，使水库泄水洞流量计算的精度有所提高，通过提高溢洪道相对开度精度，使水库溢洪道流量公式参数得以修正的做法，为解决此类问题提供了有益的借鉴。

［1］张新建.山西省漳泽水库防洪调度模拟系统［M］//水利部信息化工作领导小组办公室，水利部水利信息中心编著.水利信息化技术和建设成果研究.北京：中国水利水电出版社，2005:413-420.

［2］武汉大学水利水电学院水力学流体力学教研室.李 炜主编.水力学计算手册［M］.北京：中国水利水电出版社，2006:101、75.