动静结合 活化思维——缘起2015年高考江苏卷第14题

任虎虎

（江苏省太仓高级中学，江苏 太仓 215411）

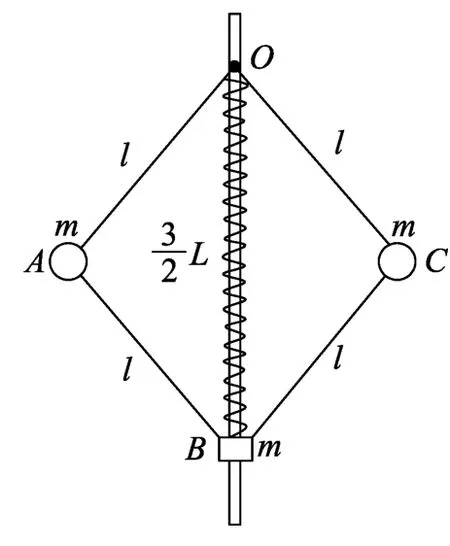
图1

（1）弹簧劲度系数k；

（2）AB杆中弹力为0时，装置的转动角速度ω0；

本题目虽然用到的都是理想化模型，例如轻杆、轻弹簧、缓慢上升等，但由于涉及到的物理量及知识点比较多，如果对知识的层次及物理过程分析不清楚就很难找到问题解决的突破口.

1 由静态表象分析因果关系 激活思维

物理问题的解决往往都要从“受力分析和运动过程分析”这两个角度开始，而受力分析需要将问题定格在一个具体的状态，如初始状态、终止状态与临界状态等.通过分析已知量和未知量之间的因果关系，对于题目中的关键点要多问几个为什么，为什么是这样而不是其他结果.利用这样的逻辑推理激活思维.

设装置静止时，OA、AB杆中的弹力分别为F1、T1，OA杆与转轴的夹角为θ1，小球受力平衡.

竖直方向：F1cosθ1＋T1cosθ1＝mg，

水平方向：F1sinθ1＝T1sinθ1，

小环受力平衡：F弹＝mg＋2T1cosθ1，

教学启示：多从因果关系的角度去分析问题，对于问题的认识就会更加深刻，更容易理清思路，也更容易找到问题的突破口，从而激活思维.

2 从静到动 活化物理过程 培养动态思维

题目中的文字和图像都是静态的表象，在通过思维加工的基础上，在脑海中形成一幅“问题图景”，想象成在你面前有这样一幅真实的景象，并且要让它“动起来”，也就是将自己置身于问题之中，培养动态思维.有了这样一幅图景，此时的问题就有“生命”了，接下来就是你与它之间的“对话”，采用这种方法很容易确定运动的临界状态.在开始阶段，学生的想象能力不是很强或者没有形成习惯，教师可以制作简易的模型来帮助学生.例如在电磁感应的教学过程中笔者利用生活中随处可见的硬纸板制作了如图2所示的模型（杆可以活动），因为对于单杆问题绝大多数问题情境都是建立在这个模型基础之上的.只是在不同的情景中，这个模型可以水平放置；可以竖直放置；也可以与水平面成θ角放置；同时可以让杆以恒定的速度向前运动；在恒定的拉力作用下向前运动；在拉力的功率恒定的情况下向前运动等等.教师在进行讲解的同时可以将制作的这个模型呈现不同的状态.通过真实的图景帮助学生建构思维意识中的问题模型.

图2

对于本题的第（2）问通过这样的方式进行分析会快速解决问题.

思维中的“问题图景”：有图2所示的装置摆在你面前，当整个装置缓慢转动的过程中，小环向上移动，弹簧长度缩短，两小球都在做圆周运动.

现在是一个动态的情景，顺着（1）问中分析平衡问题的思路，当小球在任何一个运动状态下，设OA、AB杆中的弹力分别为F2、T2，OA杆与转轴的夹角为θ2，由于做圆周运动可以得出，

竖直方向：F2cosθ2＋T2cosθ2＝mg，

水平方向：F2sinθ2－T2sinθ2＝mω2lsinθ2.

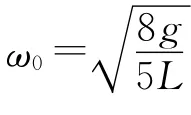
教学启示：很多动态过程都是建立在原来静态的基础上，一脉相承.教师在原来认识的基础上充分利用“问题图景”顺学而导，培养动态思维，让学生在动态的过程中找到需要的临界状态.

3 从动到静 沉淀物理思想 提升思维品质

有时物体的运动过程比较复杂，没有确定的规律，此时可以将“动”转化到“静”去分析问题.例如比较复杂的多过程问题要求运动的总路程时，利用动能定理或能量守恒的思想，只需要确定初、末两个具体状态，即可实现化繁为简、“山重水复疑无路，柳暗花明又一村”的目的.

竖直方向：F3cosθ3＋T3cosθ3＝mg，

水平方向：F3sinθ3＋T3sinθ3＝mω2lsinθ3，［注意（2）中的ω0为临界值，当ω＞ω0时，AB杆就有伸长的形变，因此对小球是拉力.］

对于小环也受力平衡：mg＋F弹＝2T3cosθ3.

运用功能关系，即系统机械能的变化量等于除重力或弹簧弹力以外的其他力做的功为

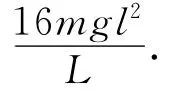
教学启示：从动到静要比从静到动的思维层次要求更高，因为从动到静必须是在对问题本质充分认识的基础上，运用归纳、整体、守恒等物理思想将问题简化，需要很高的分析综合能力.在平时教学过程中需要不断渗透物理思想方法，提升思维品质.这就要求在平时的教学过程中要慢下来，课堂上学生不再是听教师讲而被动地接受知识、套用公式，而是给学生充分思考和自我总结的时间，达到举一反三，融会贯通的目的.意在培养学生从静态到动态的问题分析推理能力以及从动态到静态的综合归纳能力，从而使知识内化，思维活化，能力外化.