电源输出功率最值问题的应用

王伟民 毕 亮

（1.太和县宫集镇中心学校，安徽 阜阳 236652；2.绿春县第一中学，云南 红河 662599）

由于电源有内阻，在电源电动势一定的情况下，由纯电阻元件组成的电路，当外电路电阻由某一数值逐渐减小，甚至降为0时，电路中的总电流不可能因外电路电阻的减小而变得无穷大，而是趋于某一数值.由公式P＝I2R可知，外电路消耗的电功率（亦即电源的输出功率）不可能因电流的增大而变得无穷大.可以证明，当外电路电阻等于电源内阻时，电源的输出功率达到最大值.

证明：如图1所示的纯电阻电路，设电源电动势为E，内阻为r，滑动变阻器接入电路中的电阻为Rx时，电源的输出功率为Px，则有

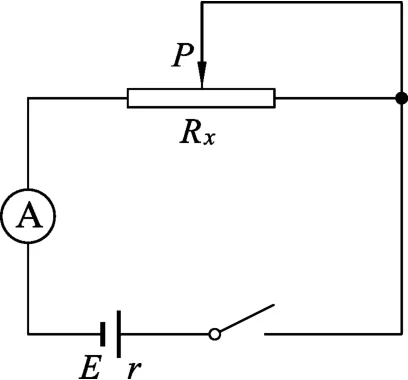
图1

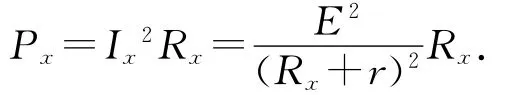
以下为该结论的一个应用.

例1.如图2所示的电路，电源电动势E＝6V，内阻r＝1Ω，保护电阻R0＝3Ω，滑动变阻器总电阻R＝20Ω，闭合开关S，在滑片P从a滑到b滑动的过程中，滑动变阻器消耗总功率的变化规律是

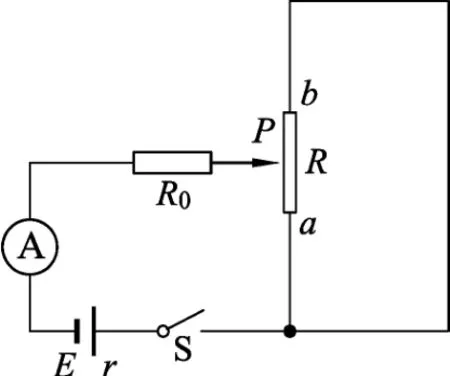
图2

（A）先减小，后增大.

（B）先增大，后减小.

（C）先减小后增大，再减小，再增大.

（D）先增大后减小，再增大，再减小.

解析：解决此类问题的常规思路是，求出滑动变阻器消耗的电功率跟滑动变阻器Pa段电阻间的函数关系式，根据函数值的变化情形来判断滑动变阻器消耗功率的变化情形.我们不妨先运用该方法进行求解.由图2可知，整个电路的连接方式为，滑动变阻器Pa、Pb两部分并联之后，再和保护电阻R0串联.

设RPa＝x，滑动变阻器连入电路的等效电阻Rx为

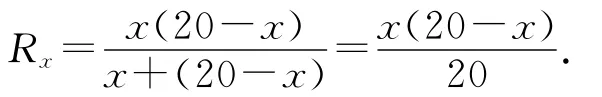
则有

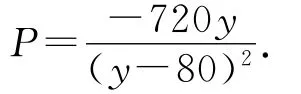
两边对y求导得

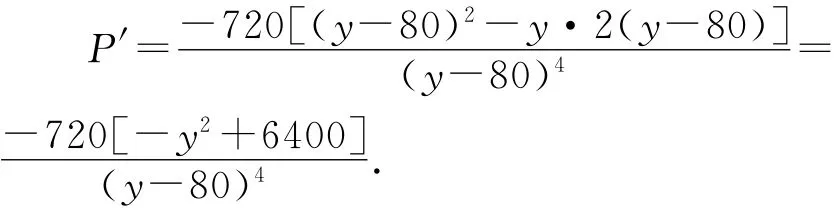
令P′＝0，得y＝±80.（80舍去，保留－80，原因是x2－20x为负数）

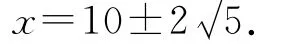
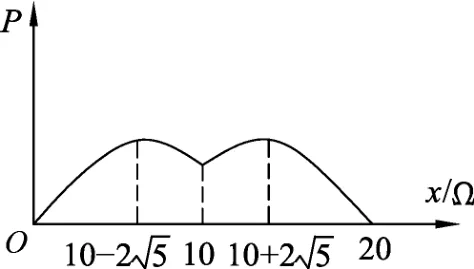
图3

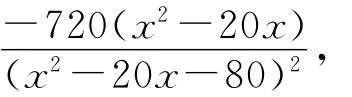
如果是考试，对于一道选择题，花费如此大的功夫，即使做了出来，也显得不“划算”——对函数

采用换元法求导，继而又解方程确定函数驻点，过程非常麻烦（如果不换元，直接求导，会更麻烦），解题过程会花费相当长的时间.那么，有没有简便方法呢？

实际上，我们可以根据电源输出功率的最大值规律来进行求解.

图2中，将r＋R0＝4Ω作为一个整体，并视为电源的“内阻”，所以，当滑动变阻器总电阻的阻值等于电源“内阻”4Ω时，滑动变阻器消耗的功率最大，由于滑动变阻器总电阻Rx与Pa段电阻x间的函数关系式

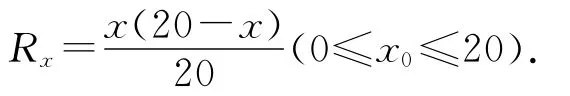
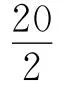
可以看出，这种解题过程，除了滑动变阻器两并联部分的最大等效电阻需要计算外（而且是非常简单的计算，口算即求出结果），整个判断过程无需动笔计算，解题过程显得干净利索，简洁明快.

当然，对该题而言，如果题目条件改变一下——滑动变阻器的阻值小于或等于（r＋R0）的4倍时（即不超过16Ω），比如滑动变阻器的阻值为12Ω，在滑片由a至b滑动过程中，滑动变阻器两部分并联的总电阻增大到最大值3Ω时（大小等于滑动变阻器阻值的1/4），滑片位置在变阻器线圈的正中间，在这一过程中，变阻器消耗的总功率一直增大，此后，滑片P由中间位置向上继续滑动时，滑动变阻器两部分并联的总电阻减小，所以，滑动变阻器消耗的总功率也跟着减小，该选择题答案选项将由原来的（D），变为现在的（B）即滑动变阻器消耗总功率的变化规律为先增大，后减小.