LT码中一种新的开关度分布

任 鹏,相 征

(西安电子科技大学通信工程学院,陕西西安 710071)

LT码中一种新的开关度分布

任 鹏,相 征

(西安电子科技大学通信工程学院,陕西西安 710071)

针对LT喷泉码,为进一步增加小度值的可译码集出现概率,限制二进制指数度分布的最大度值,提出了截短二进制指数度分布;为进一步增加大度值的可译码集出现概率,改变鲁棒孤子度分布的分布值,提出了滑动的鲁棒孤子度分布.结合这两种度分布,建立了一种新的开关度分布.仿真结果表明,新的开关度分布进行LT编码时的初始译码成功率达到了56%,整体译码成功率高于原始的开关度分布约9%～12%.

数字喷泉码;二进制指数度分布;鲁棒孤波度分布;开关度分布

目前在实际应用中的主要数字喷泉码有LT码[4]和Raptor码[5],Raptor码是对LT码的改进.关于数字喷泉码,它的设计主要包括度分布的设计、编码方法的设计和译码方法设计.其中度分布设计方法与数字喷泉码的性能直接相关,决定着译码成功率、译码代价、编译码复杂度等,设计喷泉码的关键在于构造合适的度分布函数.

度分布设计的目标是尽量使少数编码符号有较大的度数,以保证编码符号对所有输入符号的覆盖;同时使大多数的编码符号有较小的度数,以保证译码的正常运行.根据设计目标,Luby等提出了全一度分布,但由于其覆盖所有输入符号所需的编码符号非常多,因此无法在实际中得到应用.理想孤子度分布要求在每一次译码迭代循环中至少有1个度为1的编码包,但在实际中此分布的工作效率很低,因此很少被使用.基于理想孤子度分布,Luby等提出了鲁棒孤子度分布(Robust Soliton Distribution,RSD)[4],该分布引入了两个变量,以保证在每次译码时度为1的编码包的数目不是1个.虽然RSD优于理想孤子度分布,但采用RSD进行LT编码所产生的编码数据包的度值较大,在译码时可能会由于缺少足够的度值较小的编码数据包而导致译码中断.文献[6]提出的二进制指数分布(Binary Exponential Distribution,BED),其可以确保生成足够的度值较小的编码数据包,但由于大部分编码数据包的度值较小,因此,编码数据包可能没有覆盖原始数据的所有信息,会导致原始数据遗漏.此外,还有很多学者在RSD基础上提出了很多新的度分布[7-10],这些度分布都取得了较好的性能,但由于单一度分布函数的局限性,这些度分布都很难在编码包的度值大小方面取得平衡.因此,文献[11]提出将BED和RSD结合起来,建立一种新的分段式度分布函数,即开关度分布函数.随后,文献[12]又提出一种联合度分布函数,其将理想孤子度分布、BED和RSD进行组合.与单一的度分布相比,这些方法具有更良好的性能.考虑到文献[12]的方法具有很高的复杂度,且事先必须规定多个额外的参量值,因此,文中重点针对开关度分布进行改进和性能提升.强调的是,笔者所提方法同时可以扩展到联合度分布的改进中.

为进一步提高喷泉码的性能,笔者首先对BED和RSD这两种度分布函数深入探索,掌握它们各自存在的优缺点.其次,利用前一步的分析,建立了一种新的开关度分布函数.最后,对所提的开关度分布函数进行性能验证.

1 度分布函数研究

度分布函数是影响喷泉码性能的一个关键因素.由于RSD的建立是基于理想孤子度分布,所以这里分别对理想孤子度分布、RSD和BED进行分析.基于此,给出已有的开关度分布.

(1)理想孤子度分布的表达式为

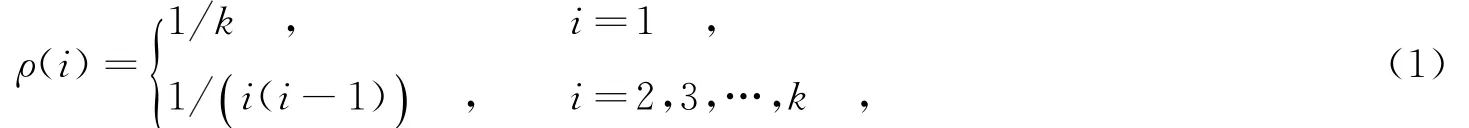
其中,k表示输入符号个数,即编码数据包数量.ρ(1),…,ρ(k)分别对应着度数从1到k的概率.理想孤子度分布在译码开始时,产生一个度为1的编码符号来恢复输入符号.然后通过迭代后,又产生一个度为1的编码符号来恢复输入符号,其整个译码过程中可译码集大小R都为1,因此,其具有最优的平均度数.但由于度选取的随机性,译码过程无法保证可译集的稳定性,可能会导致译码失败.理想孤子度分布具有较低的译码性能,在实际系统中并不可用,但它为鲁棒孤子度分布提供了理论基础.

(2)鲁棒孤子度分布.在RSD中,引入了两个参量c和δ,其中,c为常数且0＜c＜1;δ为译码失败概率的上界,一般取值为0.7,以保证在每一个译码迭代时度为1的可译码集大小为R=c ln(kδ)k1/2,而不是原来的1个.RSD函数μ(·)由理想孤子度分布函数ρ(·)和辅助函数τ(·)构成,即

李霸崖笑着说：“德公公是说，来历不明之人，才亲近不得。”但心里还是提高了警惕，掂了掂手中钓竿，“这玩意怎么这般重？”说着就盯着钓竿沉甸甸的握把发愣，显然是起了疑心。义父说过，小心驶得万年船，还是小心为妙。

图1给出了不同参量c下RSD函数中度i与概率μ之间的关系.可以看出,在不同的c下,度i计算出来的概率μ有明显差异,但其对应的整体曲线包络走向都保持一致,呈“双峰”状.虽然RSD使得译码过程更加趋于稳定,然而其产生的度值较小的可译码集较小,译码过程可能产生中断.

(3)二进制指数度分布.针对RSD的不足,提出一种BED的函数φ(·),即

其中,d表示可译码集的度值.BED函数的概率分布如图2所示.相比RSD,BED增加了度值较小的可译码集出现的概率.但是由于大部分可译码集的度值较小,可能没有覆盖全部的原始数据信息,造成原始数据遗漏.

基于BED和RSD,开关度分布ω(·)可表示为

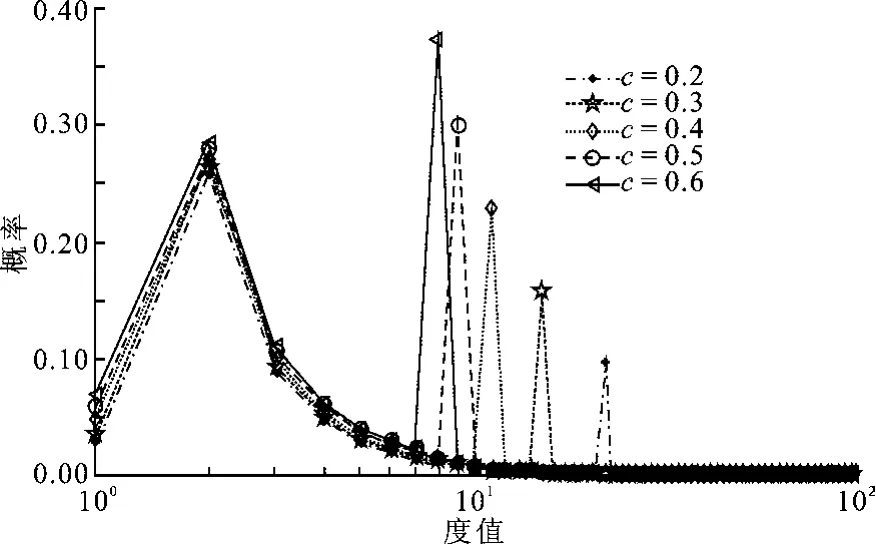
图1 RSD函数的概率分布

图2 BED函数的概率分布

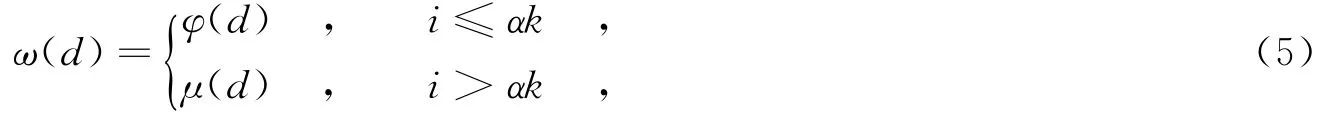
其中,α为开关点的值.

2 一种新的开关度分布

如前所述,开关度分布由BED和RSD两种度分布构成,其性能直接与这两种度分布的性能相关.根据BED的概率分布图可以看出,当度值超出某一门限(例如10)时,度值对应的概率虽然很低,但还是会影响小度值可译码集出现的概率.为了进一步降低平均度值,提高小度值的可译码集出现的概率,文中提出一种新的BED分布,即截断BED分布(Truncated-BED).根据RSD的概率分布图可以看出,第1个“尖峰”位于度值为2处,第2个“尖峰”则随着参量c的不同而变化.为了进一步提高大度值的可译码集出现的概率,文中提出一种新的RSD分布,即滑动RSD分布(Moved-RSD),来抑制第1个“尖峰”的概率,增加大度值对应的概率.最终结合Truncated-BED和Moved-RSD,建立了一种新的开关度分布,来提高数字喷泉码的性能.

(1)截断BED.由式(4)可知,BED的度值区间为[1,k],则其度值上限为k.引入参量p,0＜p＜1,则定义Truncated-BED的度值区间为[1,pk],其度值上限即为pk.Truncated-BED的函数ζ(·)可表示为

其中,D为最大度值.Truncated-BED进一步增加了小度值的可译码集出现的概率.图3给出了当k=1 000时,不同p值下所对应的Truncated-BED度分布函数的概率曲线.

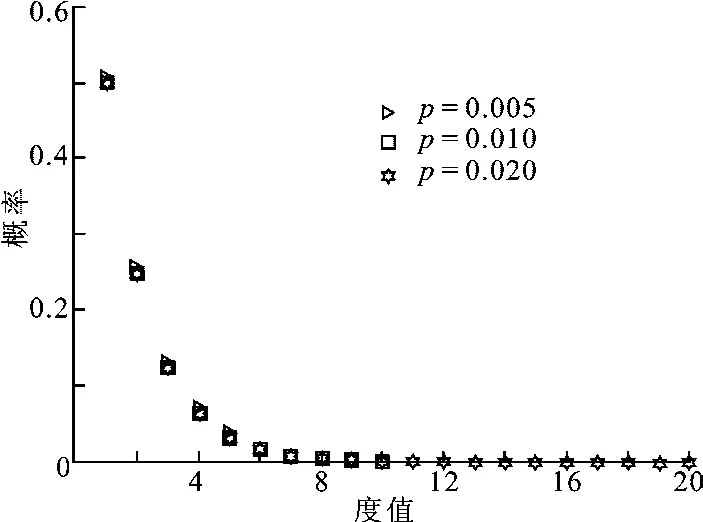
图3 Truncated-BED度分布

BED和Truncated-BED的平均度值的计算公式为

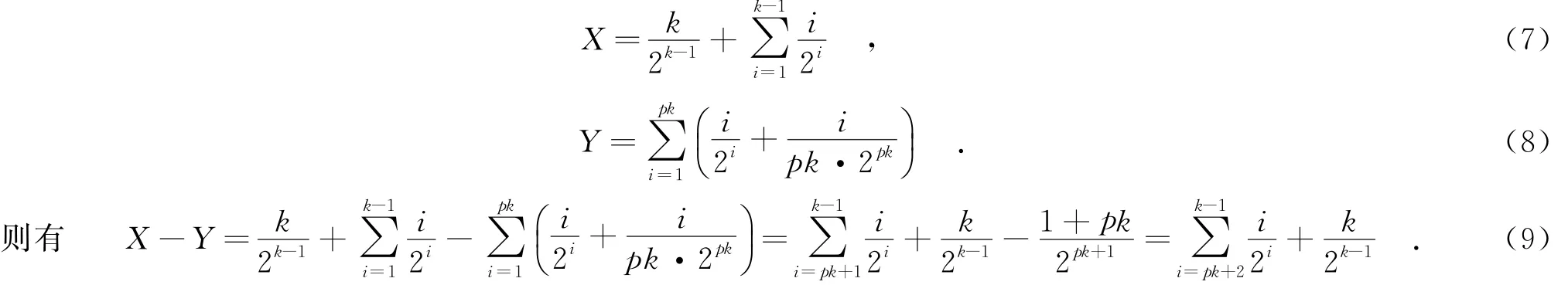
当k-1＞pk+2,即p＜1-3/k时,有X-Y＞0,即X＞Y.所以,Truncated-BED的平均度值小于BED的平均度值.

(2)滑动RSD.在RSD中,第1个“尖峰”点是由理想孤波分布ρ(i)决定的,根据式(1)可知,其处于度值

为2的位置.为了削减该“尖峰”,提升大度值可译码集出现的概率,则Moved-RSD的函数η(·)可表示为

ρ′(i)获取方法为

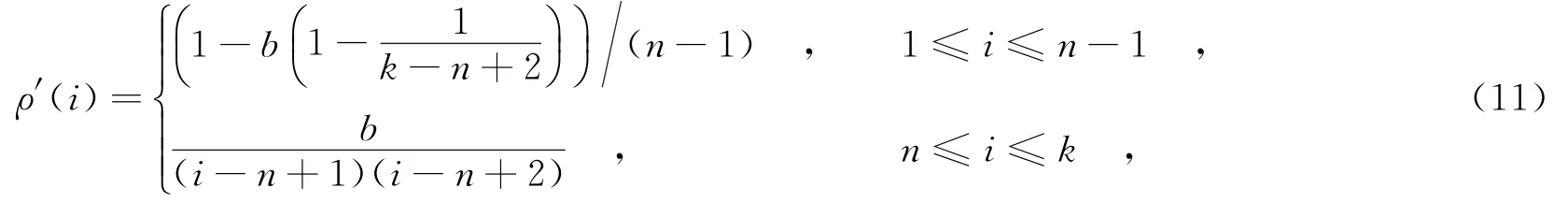
其中,n为第1峰值点,b为第1峰值系数,且0＜b≤1.

与RSD相比,Moved-RSD的第1个“尖峰”点可根据需要后移到任意度值点.图4给出了n=6,b=0.7时,Moved-RSD函数的概率曲线.

(3)新的开关度分布.Truncated-BED增大了小度值的可译码集出现概率,Moved-RSD增大了大度值的可译码集出现概率.结合这两个改进的度分布函数,建立一种新的开关度分布函数θ(·),即

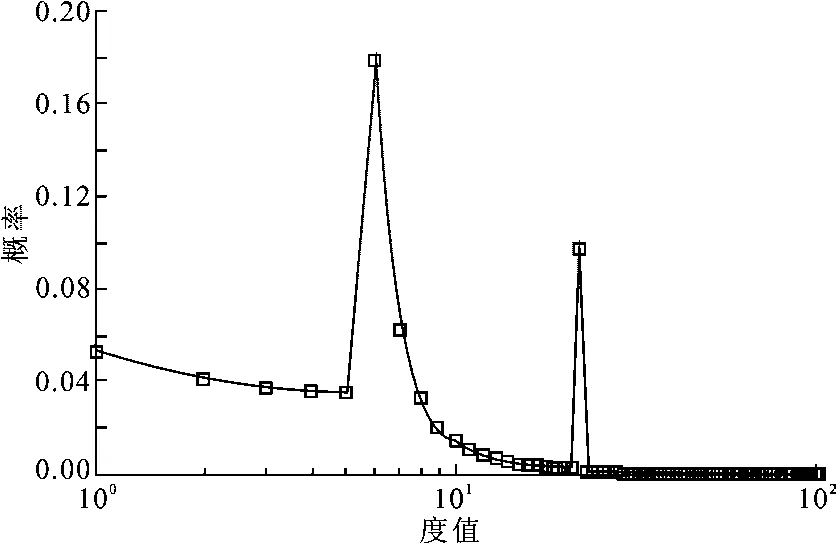
图4 Moved-RSD度分布

其中,参量α直接决定着编码器发送编码数据包的数目.在进行喷泉编码时,前αk个喷泉数据包服从Truncated-BED,保证小度值的可译码集数目足够大;后面的喷泉编码数据包服从Moved-RSD,保证大度值的可译码集数目足够大,以此进一步降低冗余信息的传输.

3 性能仿真与分析

首先,测试了在译码器成功译码时,α的取值与编码器发送的编码数据包数量之间的关系,如图5所示.从图5可以看出,当编码器原始数据包数量k分别取500、1 000和2000时,原始开关度分布与新的开关度分布都在α=0.1时达到编码数据包数的最小值.此外,在译码端成功译码时,新的开关度分布所需要的编码数据包数量少于原始的开关度分布,即译码代价更低.

其次,在码长k=1 000的条件下,测试了BED、Truncated-BED、RSD、Moved-RSD、原始的开关度分布和新的开关度分布6种不同的度分布在LT编码时,译码成功率与正确接收编码包数量之间的关系.其中,令Truncated-BED中p=0.01,RSD和Moved-RSD中c=0.2,δ=0.7,n=6,b=0.7.图6给出了仿真结果.

从图6可以看出,由于Truncated-BED的平均度值小于BED的,因此,Truncated-BED的起始译码成功率较高,但译码成功率上升最慢.由于Moved-RSD的度值1概率高于RSD的,并且提高了大度值的概率,因此,Moved-RSD的起始译码成功率高于RSD的,但有时会因为缺少足够的小度值数据包出现译码中断的情况.与单一的度分布相比,原始的开关度分布和新的开关度分布的性能较好,起始译码成功率分别达到了41%和56%,译码成功率上升速度也较快.且在相同的条件下,新的开关度分布的译码成功率高于原始的开关度分布约9%～12%.

图5 不同k值下译码成功接收编码数据包数量与α的关系图

4 结束语

喷泉码在多个前沿领域的应用使得它成为业界关注的重点,而度分布是喷泉码的核心研究内容之一.笔者对BED和RSD分别进行了改进,提出了Truncated-BED和Moved-RSD.同时将这两类度分布结合起来,建立了一种新的开关度分布.通过仿真对比,新的开关度分布具有高的起始译码成功率,且随着译码的进行,译码成功率上升很快.在同等条件下,译码成功率高于原始的开关度分布约9%～12%.

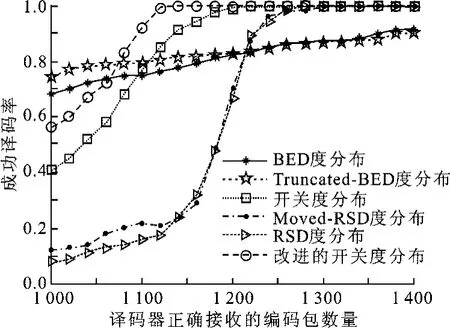
图6 不同度分布下各自的译码性能

[1]Byers J W,Luby M,Mitzenmacher M,et al.A Digital Fountain Approach to Reliable Distribution of Bulk Data[C]// Computer Communication Review:28.New York:ACM,1998:56-67.

[2]Byers J W,Luby M,Mitzenmacher M,et al.A Digital Fountain Approach to Asynchronous Reliable Multicast[J]. IEEE Journal on Selected Areas in Communications,2002,20(8):1528-1540.

[3]Zare S,Rahbar A G.Congestion Control in IPTV over PON Using Digital Fountain forward Error Correction[J]. Journal of Network and Computer Applications,2014,37(1):240-252.

[4]Luby M.LT Codes[C]//Proceedings of 43rd Annual IEEE Symposium on Foundations of Computer Science.Los Alamitos:IEEE Computer Society,2002:271-280.

[5]Shokrollahi A.Raptor Codes[J].IEEE Transactions on Information Theory,2006,52(6):2551-2567.

[6]Al Agha K,Kadi N,Stojmenovic I.Fountain Code with XOR of Encoded Packets for Broadcasting and Source Independent Backbone in Multi-hop Networks Using Network Coding[C]//IEEE Vehicular Technology Conference. Piscataway:IEEE,2009:5073564.

[7]Li L,Zhao J X.LT Codes with a New Degree Distribution[C]//Porceedings of the 2nd International Conference on Multimedia Information Networking and Security.Piscataway:IEEE Computer Society,2010:531-535.

[8]Hussain I,Xiao M,Rasmussen L K.Design of LT Codes with Equal and Unequal Erasure Protection over Binary Erasure Channels[J].IEEE Communications Letters,2013,17(2):261-264.

[9]Zhu Z L,Liu S,Zhang J W,et al.Performance Analysis of LT Codes with Different Degree Distribution[C]// Proceedings of the Fifth International Workshop on Chaos-fractals Theories and Applications.Washington:IEEE Computer Society,2012:142-146.

[10]Yen K K,Liao Y C,Chen C L,et al.Modified Robust Soliton Distribution(MRSD)with Improved Ripple Size for LT Codes[J].IEEE Communications Letters,2013,17(5):976-979.

[11]雷维嘉,刘慧锋,谢显中.开关度分布:一种改进的LT数字喷泉编码度分布[J].重庆邮电大学学报(自然科学版), 2012,24(1):34-38. Lei Weijia,Liu Huifeng,Xie Xianzhong.Switch Degree Distribution:an Improved Degree Distribution for LT Digital Fountain Code[J].Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition),2012, 24(1):34-38.

[12]Zhang M,Lei W J,Xie X Z.Combined Degree Distribution:a Simple Method to Design the Degree Distribution of Fountain Codes[C]//Proceedings of IEEE Third International Conference on Information Science and Technology. Piscataway:IEEE,2013:1089-1092.

(编辑:齐淑娟)

New switch degree distribution for the LT code

REN Peng,XIANG Zheng
(School of Telecommunication Engineering,Xidian Univ.,Xi’an 710071,China)

Truncated-binary exponential distribution is proposed for improving the occurrence of the decoding set,and Moved-robust soliton distribution is simultaneously put forward for increasing the occurrence of the decoding set.Combining the above two distributions,a new switch distribution is constructed in this paper. Simulation results show that the proposed method can reach 56%of initial decoding success,and that the total decoding success rate is higher than that by the original method by 9%～12%.

digital fountain code;binary exponential distribution;robust soliton distribution;switch distribution

TN919.3

A

1001-2400(2015)05-0043-05

2014-05-05< class="emphasis_bold">网络出版时间:

时间:2014-12-23

国家自然科学基金资助项目(61072102)

任 鹏(1984-),男,西安电子科技大学博士研究生,E-mail:pren@stu.xidian.edu.cn.

http://www.cnki.net/kcms/detail/61.1076.TN.20141223.0946.008.html

10.3969/j.issn.1001-2400.2015.05.008