巧用平移解决数学问题

杨许珍

巧用平移解决数学问题

杨许珍

在日常的教学和学习中，我们利用学过的方法去解决一些数学问题会很麻烦，如果我们在解决问题的过程中，根据题目的要求和特点，巧妙利用平移来解决问题的话，往往能把复杂的问题简单化，简化解题的程序，还可以使学生理解起来更加容易。下面的题目就是我在教学中巧用平移思想解答的几个例子。

图一

图二

例一：如上图一所示，求上面图形的周长。对于上面的题目，如果我们使用周长的定义去计算的话，是行不通的，在这个图形中我们仅知道两条边的长度，是不能算出其周长的。其次它不是一个标准的长方形，也就不能用长方形的周长计算公式去计算。但如果我们理解图形的平移的话，对这个图形做个平移变化后，如图二所示，发现图一的周长的长度与图二中长方形的周长完全的相等，那么我们就可以利用图二中长方形的周长计算公式计算出其周长。即：（18+12）×2=60.

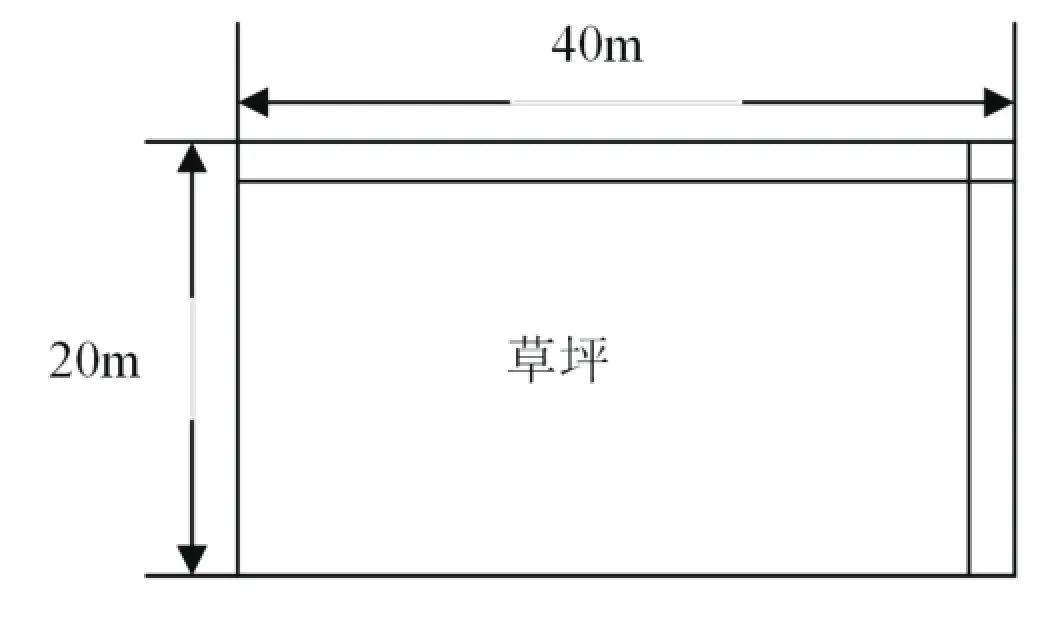
例二：在向阳小区有一个长方形的草坪，长40米，宽20米，在草坪的正中有两条小路呈十字形。（如图一所示）路宽2米，请你算一算这块草坪的面积。

学生对这个题目进行思考和分析后，做上来的答案有两种：

2.第二种思路是先算出整个长方形的面积，再算出两条路的面积，然后从整个长方形的面积中减去两条路的面积，在加上重复减去的4㎡就是从草坪的面积。解答如下：40×20=800㎡40x2=80㎡。

图一

图二

上面的两种解答思路都很好，但是计算过程却是非常的复杂，学生在解答过程中出错的情况很普遍。如果我们在这道题目中能适当的引入平移的思想，那么解答起来将会是相当的简洁。图一经平移后变为图二所示。四个小草坪合并成一个大草坪，两条路分别被平移在大长方形的边缘，如图二所示：。草坪面积计算如下：40-2=38m20-2=18m38×18=684㎡。

上面就是我在教学中，巧用平移思想解决问题的两个例子，平移作为一种数学的解题方法，如果巧妙使用的话，可以使解题起到画龙点睛的作用。对于一些题目来说，巧妙平移可以收到“踏破铁蹄无觅处，柳暗花明又一村”的神奇效果。

(作者单位：甘肃天水市麦积区渭南中心学校）