区域模型计算中庭热环境温度分布的研究

金文燕高军王昕曹倩

1同济大学建筑设计研究院（集团）有限公司

2同济大学机械与能源工程学院

3上海理工大学环境与建筑学院

4江苏绿博低碳科技有限公司

区域模型计算中庭热环境温度分布的研究

金文燕1高军2王昕3曹倩4

1同济大学建筑设计研究院（集团）有限公司

2同济大学机械与能源工程学院

3上海理工大学环境与建筑学院

4江苏绿博低碳科技有限公司

通过分析中庭室内热环境分布的特性，介绍了利用温度基准区域模型来计算中庭室内热环境的详细方法，并给出了在自然通风时自然通风量的计算。利用区域模型计算了上海某一中庭在不同划分高度时的主体和壁面温度分布，并与实测值相比较，以研究划分高度对计算结果准确性的影响。比较结果表明：在利用区域模型计算高大空间的温度分布时，设定区域高度宜小于1m，得到的结果较为准确；自然通风能够有效地改善室内温度分层，为建筑节能提供了一种思路。

区域模型 中庭 热环境

0 引言

中庭作为一种高大的开放空间，具有良好的空气品质及突出的公共性，为室内人员提供了良好的沟通交流空间[1]。然而，作为一种特殊的建筑形式，中庭的开敞性和通透性以及自然空间的营造使得其室内的热环境更为复杂，热环境的设计和控制难度更大。为了满足中庭室内舒适度要求，优化气流组织，降低能耗，需为中庭环境的预测开发一种有效的工具。

中庭热环境的影响因素较多，主要包括：室外气象条件、围护结构的热惰性、室内人员、设备、灯光散热散湿等，其室内温度分层现象明显，呈现出“温室效应”与“烟囱效应”，目前，对于高大中庭热环境的研究方法有：实验法和计算机数值模拟法（Computational Fluid Dynamics）。对于实验方法，由于高大中庭体量较大，实验条件往往难以实现。因此，更多学者便利用计算机模拟技术即系统控制模拟软件或者能耗模拟软件，通过独立[2～4]或联合模拟[5]的方式研究中庭热特性及控制方法。

然而，虽然CFD方法是高大中庭热环境研究的一种有效手段，但是其计算结果对网格的划分具有较大的依赖性，计算的收敛性需要不断调试；另一方面，其过于详细的计算参数对工程的指导意义有限。因此，需寻找一种合适的方法，既能准确描述中庭热环境的分布特点，又能避免不必要的资源浪费。

因此，本文引出了温度基准区域模型，该模型是一种介于求整体参数的集点参数法与CFD方法之间的一种计算方法，其基本思想是：室内空气温度在水平方向上均匀一致，将室内空气体积按其传热特性不同在垂直方向上划分成多个控制体，通过对各个控制体建立空气质量和能量平衡方程以求解区间的空气流动与各控制体温度分布[5～6]。

1 温度基准区域模型

区域模型方法摒弃了CFD方法中对网格的过细划分，通过对高大空间热特性的分析，合理地认为水平方向上温度分布呈两种形式：受边界条件影响的边界层内气流运动，以及主体区域内的气流运动（如图1、2）。对于非核心式中庭，边界层内的气流受室外气象条件的影响较大，在夏季形成沿壁面上升的热流，而在冬季则为沿壁面下降的冷流。而中心区域内的气流则在内扰和与边界换热的综合影响下，受浮升力的作用往上运动。边界层内的气流不仅存在垂直方向上的运动，由于与主体区域的气流存在温差，因此在水平方向上存在热质交换。

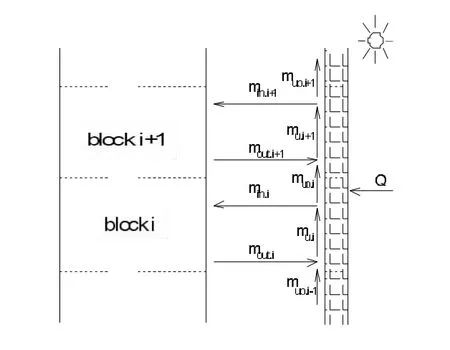
图1 边界层气流运动（沿热壁面上升）

图2 区域模型划分

现代建筑为了增加高大中庭的通透性，很多中庭采用玻璃幕墙结构，因而室内环境更加易受外界条件的波动影响，尤其太阳辐射在中庭室内的分布对其影响较大。本文在利用区域模型分析室内的热环境时，首先利用蒙特卡洛法计算中庭室内太阳辐射分布[7]。由于中庭室内主体温度分布与壁面温度分布相互耦合，因此在计算时，首先假定中庭主体区域温度分布，将太阳辐射得热计算结果作为边界条件导入表面热平衡模型，求得中庭室内的壁面温度与边界层内的平均温度。中庭表面的热平衡方程为：

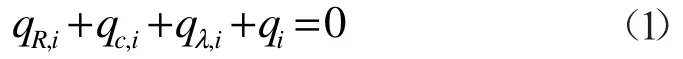
式中：qR,i为表面i与其他表面的单位面积辐射换热量；qc,i为表面i与边界层内的空气单位面积对流换热量；qλ,i为表面i的单位面积导热换热量；qi为表面i的内热源产热量，计入太阳辐射量。

由图1、2可知：边界区域内上升气流的运动可描述为：下一边界区域的气流上升后，部分进入主体区域，部分与主体区域的出流混合后继续上升到下一边界。对于水平方向，由于边界区域与主体区域存在质交换，另一方面，由能量守恒可知：壁面与主体区域的自然对流传热量等于边界层与主体区域质交换的传热量，由此对于同一高度边界区域与主体区域有：

根据质量守恒：

由能量守恒：

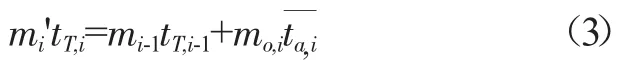
公式中的部分参数可参照图1、2，tT,i表示边界上升（或下降）流的温度，为主流区域的空气温度。由上面两式可求得边界层内的气流运动量以及与主体区域的质交换量。

最后，针对主体区域，其热环境的变换受到以下几个方面的影响：①区域内热源；②与边界层的热质交换；③与相邻边界的热质交换。因此，其质量与能量平衡方程可如下表示：

上式中，ms表示区域内由于空调、通风等引起区域内的质量的增加或减少量，Qs表示区域内部的热源（如室内热扰量）。cbAi-1(ti-1-ti)与cbAi(ti+1-ti)表示相邻区域由于温度差存在的热交换量。由以上公式可求得各区域间的气流运动量以及区域的整体温度参数。

2 自然通风

为了进一步改善中庭的热环境，目前越来越多的中庭考虑利用自然通风来给中庭降温。因此，本文进一步分析了自然通风时通风量的计算方法。

将空间竖向共分成N个区，其中若自然通风所占高度区域为Nv个，对于自然通风入口和出口处建立伯努利方程：

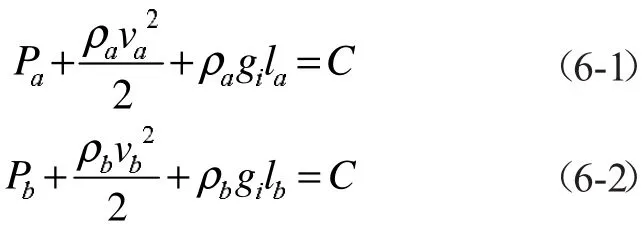
式中：Pa、Pb为a、b处的绝对压力；ρa、ρb为a、b处的密度值；la、lb为a、b处的相对同一平面的高度；gi为各区的重力加速度；C为常数。

联立二方程，并考虑由于高度不同温度变化带来的密度变化，此处不再详述，可得：

由于室外风的风速和风向经常变化，风压不是一个稳定的因素。为了保证自然通风的设计效果，在实际计算时仅考虑热压的作用，一般不考虑风压。

根据连续性方程，对于自然通风的进口和出口，可建立的风量平衡方程：

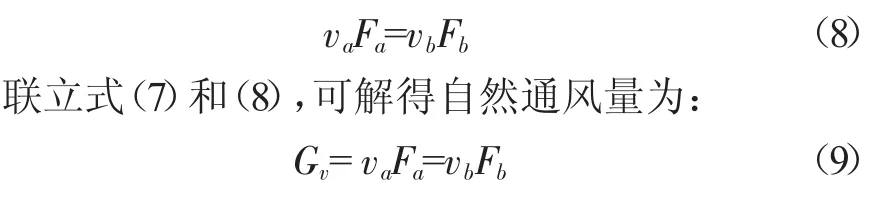
3 实例验证

前面已对温度区域模型进行了深入的分析，并建立了完整的数学模型。本节拟利用区域模型计算某中庭的温度分布，并与实测值进行比较，以验证理论模型的正确性及适用性。验证对象选取上海闵行区某生态示范楼。

该楼总建筑面积1994m2，钢混主体结构，南面两层、北面三层；西侧为建筑环境实验室，东侧为生态建筑技术产品展示区和员工办公区，中部为采光中庭与天窗。

上海理工大学王昕[8]等人对于生态楼的热环境进行了一系列的测试研究，测试了夏季（7月12日）各不同工况下的中庭内的温度分布，工况具体情况如表1。

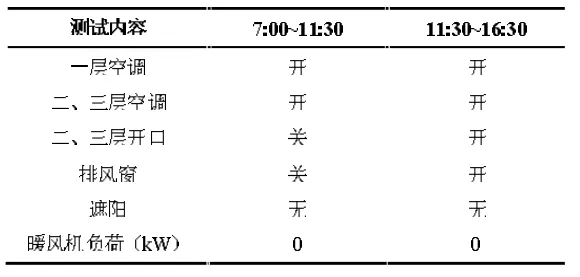
表1 测试工况

本节计算时先利用基于蒙特卡洛法计算出在7月12日各时刻的太阳辐射量，并将其作为边界条件导入到边界壁面温度的计算。

区域如何划分一直是区域模型研究的一大重点，区域划分的方法，也就是对计算体量控制体的定义，对最后的结果影响也因不同工况而异。一般情况下，在缺乏流场详细信息的情况下，若想得到较为精确的结果，则对区域划分的疏密要求较高。但是，区域模型不同于CFD的一大优点在于：CFD模拟对于网格的疏密划分依赖性较高，要求计算机内存较大，计算结果的收敛性还需要不断的调试。而区域模型若为了保证其假设前提，即区域中的各参数基本一致，则可能需不断地细划区域，最终失去了区域模型的应用意义。

目前，对于区域的划分，研究者大多首先对问题进行初步认识，在已有经验的基础上，较为合理的划分，比如区域模型发展的初期，研究者按照高大空间的垂直温度分布，研究了二区域、多区域模型，而后，随着对壁面边界层的研究深入，研究者将边界层的流动及换热引入了区域模型的研究，认为可将区域分为主流区域以及靠近壁面的边界层流动，这样的划分具有一定程度的合理性[9]。

本文为了研究区域划分高度对计算结果的影响，对生态楼进行了以下高度的分区：0.5m，1m，2m，并进行计算，将计算结果与实测值进行比较，分析不同划分数量对计算结果的影响。

本中庭的结构较为特殊，一层与大厅联通，二层与办公室的走廊、室外花园联通，中庭屋顶为坡屋顶形式，利用屋面自然采光，模型验证时，为了简化计算，将中庭假设为一个封闭空间，即不考虑联通部分对中庭环境的影响，但仍考虑空调对中庭的影响，即中庭的一层部门设为空调区域。在区域划分时，将墙体进行等高度划分，将坡屋顶所在空间划分为一个区域，划分方法如图3所示。

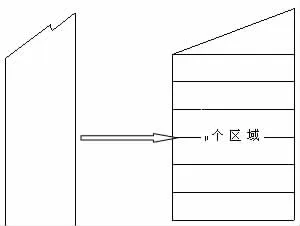
图3 模型简化与区域划分

为了进一步比较自然通风对中庭室内温度分布的影响，本文计算了在无自然通风和有自然通风条件下各区域温度与实测值的比较如图4～9所示。

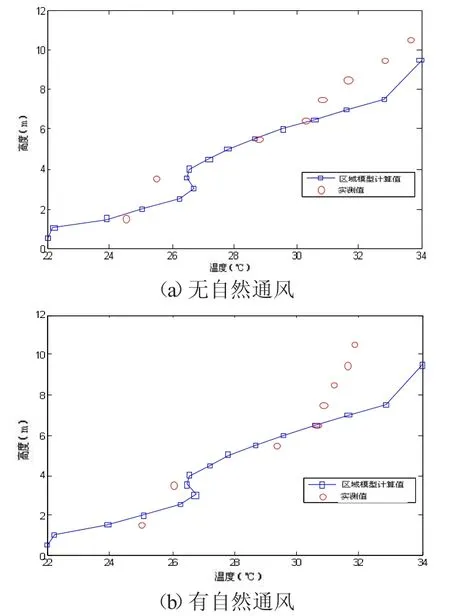
图4 按0.5m高度分区时的区域温度

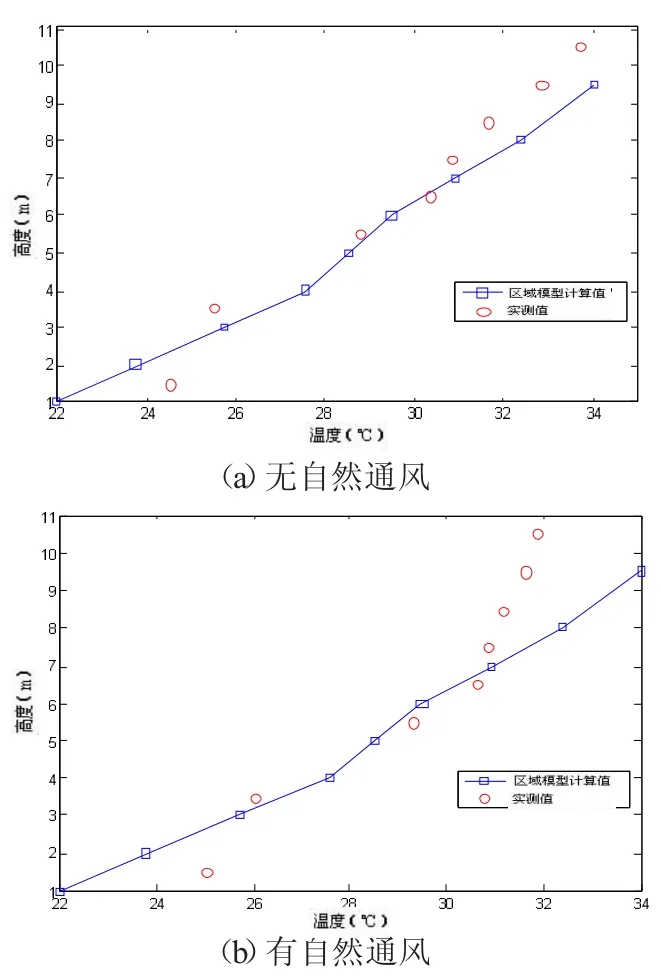
图5 按1m高度分区时的区域温度

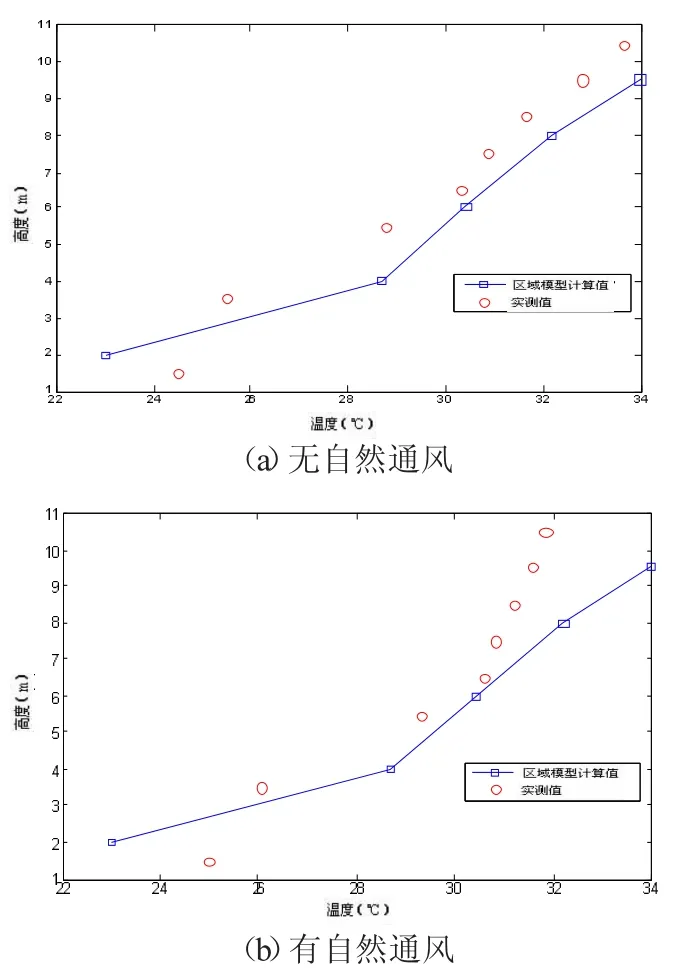
图6 按2m高度分区时的区域温度

按照三种不同的分区高度，其中庭各向内表面温度如下所示：

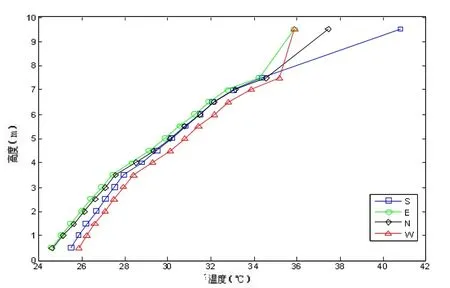
图7 0.5m分区高度中庭内表面温度

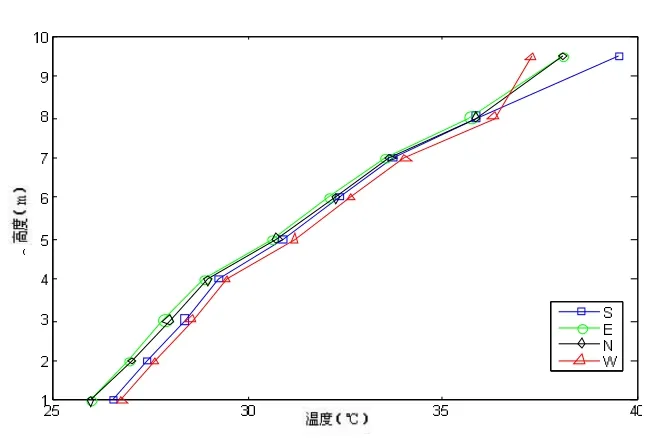
图8 1m分区高度中庭内表面温度

图9 2m分区高度中庭内表面温度

由以上结果可以得知：研究分区高度对计算结果的影响时，将分区高度设为0.5m、1m、2m，可以看到，当分区高度为0.5m、1m时，区域模型的计算值与实测值相差较小，吻合度较好；但是，当分区高度达2m时，模型计算值整体偏离了实测值，即区域高度为2m时，区域模型的假设已经偏离了实际情况，区域内的物理参数并非均匀分布，因此，此时的各区温度并不能表示该区域的实际情况。

比较中庭在无、有自然通风条件下的温度分布可知：在无自然通风的情况下，区域模型计算中庭温度分布时，若分区高度合理，计算值与实测值偏差较小，吻合度较好。但在利用区域模型计算自然通风的通风量时，并未考虑自然通风对区域温度场的影响。而众多已有研究结果表明，对于高大空间，自然通风能够显著改善上部空间温度分布，生态楼的实测结果也显示：在有自然通风的情况下，由于通风的影响，空气团间的热质交换较为频繁，带动底部温度较低的气流往上运动，与上部热空气发生混合，进行能量交换，因此，底部温度较无自然通风时略高，但是，随着建筑高度的增加，温度分层情况较无自然通风时有所减弱，最高温度相差达2.73℃。

4 结论

1）在利用区域模型计算高大空间的温度分布时，分区高度对计算结果的准确性至关重要。本文建议设定区域高度小于1m；

2）中庭自然通风能够有效地改善中庭室内的温度分层情况，降低中庭上部空间的整体温度，从而降低中庭及相邻空间的建筑能耗；

3）在计算模型正确建立、高度合理划分的基础上，温度基准区域模型能够较为准确的计算了中庭高度内的温度分布，为高大中庭的负荷计算、能耗模拟提供了一种有效的计算手段。

[1]理查·萨克森著,戴复东,吴庐生译.中庭建筑开发与设计[M].北京:中国建筑工业出版社,1990

[2]宋芳婷.中庭热环境动态模拟方法研究[D].北京:清华大学, 2004

[3]赵林,李念平.住宅建筑中庭内自然通风的数值模拟[J].科技导报,2009,27(2):73-77

[4]杨建坤,张旭.自然通风作用下中庭建筑热环境的数值模拟[J].暖通空调,2005,35(5):26-29

[5]J Lebrun,P Ngendakumana.Air circulation induced by heating emitters and corresponding heat exchanges along the walls:test room results and modeling[A].In:Proc.ROOMVENT‘87[C]. Srockolm,Sweden:1987,Session 2a,Paper 6

[6]高军.建筑空间热分层理论及应用研究[D].哈尔滨:哈尔滨工业大学,2007

[7]金文燕,王健,翁骁炜.中庭室内太阳辐射再分配的研究[J].流体机械,2010,40(10):84-86

[8]王昕.大空间建筑复合通风运动机理与理论模型研究[D].上海:上海理工大学,2008

[9]S Togari,Y Arai,K Miura.A simplified model for predicting vert -ical temperature distribution in a large space[J].ASHRAE Trans, 1993,99(1):84-99

Re s e a rc h on Zona l Mode l to Ca lc ula te the The rm a l Dis tribution of Atrium s

JIN Wen-yan,GAO Jun,WANG Xin,CAO Qian
1 Architectural Design&Research Institute of Tongji University
2 School of Mechanical Engineering,Tongji University
3 School of Environment and Architecture,University of Shanghai for Science and Technology
4 Jiangsu Lubo Low Carbon Technology Co.Ltd.

Based on the analysis of the thermal environment of atrium,zonal model with the benchmark of temperature is introduced to calculate the distribution of indoor temperature.The model is used to predict the thermal environment of an atrium in Shanghai,and the result is compared with that of test.It indicates that when the height of every zone is refined to less than 1m,the result of zonal model is consistent with that of the test.The results with and without natural ventilation are compared and it reveals that natural ventilation can effectively reduce the temperature stratification of atrium.It may be a useful method of buildings’energy saving.

zonal model,atrium,thermal environment

1003-0344（2015）01-027-5

2013-10-17

金文燕（1989～），女，硕士研究生；上海市四平路1230号同济大学建筑设计研究院536室（200092）；E-mail:misaly2006@126.com

上海市科委科技攻关课题（09dz1207704）