VRV-VAV联合空调系统基于负荷预测的优化控制
2015-07-20王启迪晋欣桥杜志敏祝用华
王启迪 晋欣桥 杜志敏 祝用华
上海交通大学制冷与低温工程研究所
VRV-VAV联合空调系统基于负荷预测的优化控制
王启迪 晋欣桥 杜志敏 祝用华
上海交通大学制冷与低温工程研究所
针对VRV-VAV联合空调系统,本文提出了一种优化控制策略,通过改变屋顶机送风温度设定值实现了系统的优化控制。采用状态参数自适应递归和时间序列分析法建立了系统能效比的预测模型,并针对模型的问题对其进行了修正,进而提出一种组合预测模型。修正后的模型平均误差为0.05%,最大误差仅为0.342%,将其应用于系统的优化控制节能率可以达到6.7%。
VRV-VAV联合空调系统 变送风温度 节能 优化控制策略 能效比预测
变制冷剂流量(VRV,Variable Refrigerant Volume)空调系统因其良好的部分负荷性能及显著的节能效果已经广泛应用于商业建筑中。近年来,针对VRV空调系统无法引进新风的弊端,很多学者提出将变风量(VAV,Variable Air Volume)空调系统作为VRV空调系统的新风处理单元,并对此联合空调系统进行了大量的仿真研究。然而这些研究大多侧重于仿真算法的建立,仿真模型的搭建,压缩机转速、膨胀阀开度、制冷剂流量分配、送风量的控制策略及模型的计算速度和稳定性上[1~4],极少对系统的节能潜质进行分析和探索。在建筑能耗已占到总能源消耗的27.8%[5]的今天,对于降低联合空调系统能耗的研究具有重要意义。
VRV-VAV联合空调系统的VRV侧、VAV侧均承担了一部分室内负荷,本文研究了两者的最佳负荷分配比,提出了一种优化控制策略。对于系统能效比预测的精度是影响优化控制策略节能效果的主要因素。传统空调系统负荷预测模型有的精度较低,有的过于复杂,影响仿真模型计算速度和控制稳定性[6,7]。本文建立了VRV-VAV联合空调系统的能效比预测模型,针对模型的问题对其进行了修正,并将修正后的模型应用于系统的优化控制。
1 系统介绍
本文所研究的系统是一拖六的VRV系统和VAV系统组成的联合空调系统(图1),用于上海某办公楼六个办公房间的供冷,每间房间的面积均为32m2,室内人员、设备、照明负荷的设定满足公共建筑设计节能标准(GB 50189-2005)。VRV侧依据室内负荷的变化调节制冷剂流量,压缩机在不同转速下连续运行,主要包含两种控制策略:通过调节室内机膨胀阀的开度控制房间温度;通过调节压缩机转速控制其吸气过热度。VAV侧由直膨式屋顶机和通风设备组成,通风设备依据室内CO2浓度调节送风量,主要包含两种控制策略:通过调节VAV风阀的开度控制室内CO2浓度;根据送风静压的变化调节风机转速。屋顶机将新风处理到设定温度以减小VRV侧的新风负荷,主要包含两种控制策略:通过调节膨胀阀的开度控制送风温度;通过调节压缩机的转速使其吸气过热度保持稳定。

图1 VRV-VAV联合空调系统
2 优化控制策略
本文以Trnsys软件为平台建立了如图1所示的系统模型[8]。VAV侧的设计初衷主要是为了满足室内的新风要求,但它却不可避免地承担了一部分室内负荷,因此,对于某一时间一定的系统负荷,如何动态地、最优地分配VAV侧和VRV侧所承担的负荷,以使整个系统能耗最小是优化控制策略研究的核心内容。
系统的新风量是根据室内CO2浓度调节的,新风量不受负荷的影响,风机能耗是固定的,因此能耗优化的主要目标是系统压缩机能耗最小。压缩机的能耗是由其额定功耗和实际运行条件的修正得到的如方程(1)[9~11]。

式中:Q表示系统的制冷量;EIR是能量输入比系数,指系统在由不同的室内空气湿球温度和室外空气干球温度所确定的不同工况下的标定耗电量和标定制冷量之比[10],即系统在不同工况下的能效比COP的倒数,如式(2)所示;RTF是部分负荷修正系数。

部分负荷修正系数RTF表达式如方程(3)~(5)所示。

式中:PLR是部分负荷比,工程上用制冷量Q和设备的额定容量Qrated的比值表示;PLF表示压缩机启停导致的效率损失修正系数,用压缩机部分负荷运行时的效率ηpartload和稳定运行时的效率 ηsteadystate的比值表示,压缩机连续运行时,PLF等于1。
根据式(1)~(5)可以得到系统压缩机总能耗Wtotal如下:

式中:WVRV、WRT分别表示VRV和屋顶机的压缩机功耗;Qneed表示当前时刻总的冷负荷;x表示VRV部分承担的负荷率。

由式(11)可知,对于当前时刻,当VRV和VAV同时开启时,只要预测出VRV和屋顶机的能效比COPVAV和COPRT,就可以求得使得式(11)所示的二次函数取得最小值的负荷比x,依据式(12)将x转化为屋顶机送风温度的设定值即可实现系统的优化控制;当室内温度不大于设定值且室外空气焓值小于室内空气焓值时,VRV和屋顶机的压缩机均关闭,只开启通风设备;当室内CO2浓度低于设定值时,只开启VRV机组。具体的控制策略流程图如图2。


图2 优化控制流程图
3 能效比预测模型的建立
空调系统的能效比既受环境等外界因素影响,又与系统自身的特性有关,全面考虑以上影响因素,本文分别采用状态参数自适应递归法和时间序列分析法建立VRV-VAV联合空调系统的能效比预测模型。
3.1 状态参数自适应递归模型
自适应递归法利用系统对过去较长一段时间的了解和适应,在线、实时地调整系统的过程参数,本文采用常用的带指数遗忘的最小二乘递归法对影响系统能效比的状态参数自适应递归[11]。影响空调系统的能效比的主要参数有室内空气湿球温度,室外空气干球温度、蒸发温度、冷凝温度及压缩机频率[11~13],无量纲化得到能效比预测模型:

式中:Tout,Tin,Te,Tc,f分别表示室外空气干球温度,室内空气湿球温度、蒸发温度、冷凝温度及压缩机频率;Tout,norm,Tin,norm,Te,norm,Tc,norm,f,norm分别表示标准工况下的室外空气干球温度,室内空气湿球温度、蒸发温度、冷凝温度及压缩机额定频率。k,m,n,p,q,r为自适应拟合的、随时间变化的时变系数。
3.2 时间序列分析模型
对于平稳的、独立随机的时间序列,可以根据历史数据预测未来数据。许多预测目标的时间序列并不总是可以简单地使用单一的自回归过程或移动平均过程描述,而是兼有自回归过程和移动平均过程的特征,即当前时段的观测值αt可以表示为平均值μ、过去p个历史时段的观测值、过去q个历史时段的预测误差和一个当前时刻随机误差线性组合,如式(15)所示[14]。

由于本文系统的时间序列是非平稳的,需要进行平稳化处理。对该序列的值进行如式(17)所示的一阶差分后得到平稳的时间序列αt:

式中:αt+1为当前时刻的预测值;αt,αt-1分别为前一个和前两个时间步长时刻的观测值;et为前一时间步长时刻的预测误差;,θ1,μ为反映历史样本数据的特征值。
3.3 预测结果及分析
本文以上海6月15日的能效比为历史数据,对上海夏季典型日8:00到20:00的能效比进行预测,两种预测模型的误差如图3、图4和表1所示。

图3 状态参数递归模型误差分布图

图4 时间序列模型误差分布图
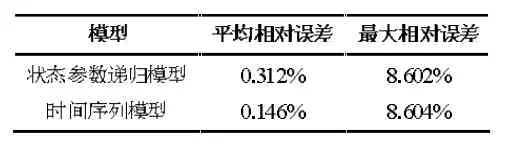
表1 预测模型误差表
可以看出,两种预测模型在部分时间内能够保证较高的精度,但精度很不稳定,在某些时间存在较大的误差,最大误差超过了8%,严重影响了优化控制的稳定性和节能效果。因此提高预测模型的精度是十分必要的。
4 能效比预测模型的修正
4.1 修正方法
很多学者对空调负荷预测的大量研究表明,两种或两种以上无偏的单项预测按照加权系数的方法,可以组合出优于每个单项预测的预测结果[15~17]。在两种预测模型,状态参数自适应递归模型反映了环境、负荷等外部参数对系统能效比的影响,时间序列模型按照历史数据的变化趋势预测未来,更多的反映了系统自身的固有属性,两种模型都是无偏预测,因此将两种模型按照式(19)的方法组合起来,可以得到综合反映系统内部因素和外部因素的更为全面准确的能效比预测模型。
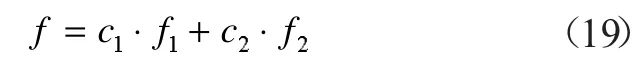
式中:f表示组合预测值;f1和f2分别表示状态参数自适应拟合模型预测值和时间序列模型预测值;c1和c2分别表示两种预测模型所占的权重,它们是随时间变化的、自适应校正的时变系数,满足c1+c2=1。
设i时刻的组合预测值为fi,观测值为yi,则由式(19)可以得到N时刻的组合预测值fN:

式中:f1N,f2N分别表示N时刻自适应拟合模型和时间序列模型的预测值;c1N,c2N为该时刻两种模型的权重,它是根据前N-1个时刻误差平方和最小的原则自适应得到的,即c1N,c2N使得下式取得最小值:

式中:J表示假设权重系数为c1N,c2N时前N-1个时刻的预测误差平方和;ei表示假设权重系数为c1N,c2N时i时刻的预测误差;f1i,f2i分别表示i时刻两种模型的预测值。
用eji表示时刻第j种预测方法的误差(j=1,2),式(21)可简化为:

定义R=[1,1]T,则约束条件c1N+c2N=1可以表示成:

略去推导过程,可以得到,满足约束条件并且使J=KTEK取得最小值的最优加权系数向量为:

对于任一时刻,都可以依据式(24)求得一组对应的加权系数c1、c2,将其代入式(19)便可得到该时刻的预测值。
4.2 预测结果及分析
采用修正的能耗预测模型根据同样条件下对上海同一天(6月15日)的能效比进行预测,误差分布如图5所示。修正后的预测模型达到了很高的精度,平均误差为0.05%,最大误差仅为0.479%。

图5 修正模型误差分布图
5 优化控制结果及分析
本文将修正后的预测模型应用于上述的优化控制策略,所选取的上海一典型日的室外温度如图6所示。屋顶机和VRV压缩机额定功率分别为2.942kW、14.670kW,额定工况下的能效比均为3.098,室内温度设定值为24℃。机组运行时间为8:00至20:00,8:18开启优化控制运行模式至20:00终止。

图6 室外干球温度
室内温度实际值和屋顶机送风温度设定值如图7~8。从图中可以看出,六个办公房间的室内温度均平稳地控制在设定值附近,屋顶机送风温度设定值随着其所占的负荷比连续变化,平均送风温度设定值为22.6℃。为研究优化控制的节能效果,将优化控制的结果分别与屋顶机送风温度设定值T为定值21℃、23℃、25℃的结果相比较,四种运行模式的制冷量和能耗结果如图9~10和表2所示。从结果中可以看出,系统在不同运行模式下总的制冷量是相同的(这是由总的冷负荷决定的),只是VRV和屋顶机的制冷量分配比发生变化;四种运行模式的风机能耗相同,这是由于新风量不受负荷的影响,优化控制运行模式的压缩机总能耗最小,三种定送风温度设定值的运行模式中,送风温度设定值在优化控制送风温度设定值的均值附近(即T=23℃)时,相较与其他两种定送风温度设定值的运行模式(即T=21℃,T=25℃),系统能耗较小。

图7 房间温度值

图8 屋顶机送风温度设定值
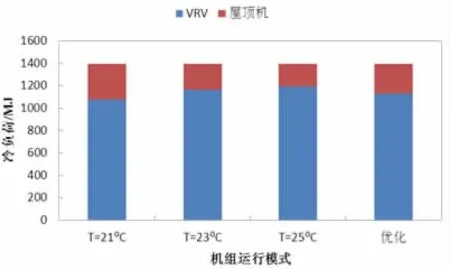
图9 四种运行模式机组制冷量

图10 四种运行模式机组能耗

表2 四种运行模式机组能耗
用节能率η表示优化控制的节能效果,η的计算公式为:

式中:Wi(i=1,2,3)分别表示送风温度设定值为定值T=21℃,T=23℃,T=25℃时的系统能耗,W表示优化控制运行模式下的系统能耗,优化控制运行模式与三种定送风温度设定值的运行模式相比较的节能率结果如表3所示。

表3 优化控制运行模式节能率
6 结论
VRV-VAV联合空调系统的VRV和VAV侧均承担一部分室内负荷,本文研究了其最优负荷分配比,提出了一种优化控制策略。准确预测系统的能效比是优化控制策略实现的关键,本文采用状态参数自适应递归和时间序列法建立了系统能效比的预测模型,并针对模型的问题对其进行了修正,修正后的模型平均误差为0.05%,最大误差仅为0.342%。将预测模型应用于系统的优化控制,根据负荷条件实时地动态分配联合空调系统VRV侧和VAV侧的负荷,通过改变VAV侧送风温度的设定值实现系统的优化控制,结果表明:相对于典型的三种定送风温度设定值的运行模式,优化控制运行模式的节能率分别可达到6.7%,1.6%和2.2%,具有较为显著的节能效果。
[1]S Q Shao,W X Shi,X T Li,et al.Performance representation of variable-speed compressor for inverter air conditioners based on experimental data[J].International Journal of Refrigeration,2004, 27(8):805-815
[2]Q Tu,Z P Feng.Heating control strategy for variable refrigerant flow air conditioning system with multi-module outdoor units[J]. Energy and Buildings,2010,42:2021-2027
[3]邵双全,梁楠.多联式空调制冷系统动态仿真研究[J].制冷学报,2011,32(1):16-22
[4]J M Choi,Y C Kim.Capacity modulation of an inverter-drivenmulti-air conditioner using electronic expansion valves.Energy, 2003,28(2):141-155
[5]Zhi-Sheng Li,Guo-Qiang Zhang.Application and development of solar energy in building industry and its prospects in China[J]. Energy Police,2007,35:4121-4127
[6]胡文斌,杨昌智,罗滨滨.灰色拓扑预测在暖通空调负荷预测中的应用[A].见:全国暖通空调制冷2000年学术年会资料集[C].2000,604-607
[7]糜作维.基于BP人工神经网络的空调降温负荷预测[J].电力需求侧管理,2010,12(4):27-30
[8]Y H Zhu,X Q Jin,Z M Du,et al.Generic simulation model of multi-evaporator variable refrigerant flow air conditioning system for control analysis[J].International Journal of Refrigeration, 2013,36(6):1602-1615
[9]Zhou Y P,Wu J Y,Wang R Z,et al.Energy simulation in the variable refrigerant flow air-conditioning system under cooling conditions[J].Energy and Buildings,2007,39:212-220
[10]Henderson H,Huang Y J,Parker D.Residential Equipmen t Part Load Curves for Use in DOE-2(LBL report No.42175)[R].Berk -ley,CA:Lawrence Berkley Laboratory,2008
[11]周宴平.变频多联空调能耗模型的建立[D].上海:上海交通大学,2007
[12]杨天.基于变蒸发与冷凝温度的变频多联空调系统能耗仿真分析和实验验证[D].上海:上海交通大学,2010
[13]赵伟.多联式空调系统部分负荷特性分析[D].北京:清华大学, 2009
[14]刘培俊.冰蓄冷空调系统的在线优化控制策略研究[D].上海:上海交通大学,2005
[15]姚烨,连之伟.基于AHP的空调负荷组合预测研究[J].哈尔滨工业大学学报,2004,36(9):1269-1275
[16]J M Bates,C W J Granger.The combination of forecasts[J].Oper -ation Research Society,1969,20:451-468
[17]Robert L Winkler,Spyros Markridakis.The combination of forec -asts[J].Wiley for the Royal Statistical Society,1983:150-157
Optim a l Control Stra te gy of a VRV-VAV Com bining Air Conditioning Sys te m ba s e d on the Loa d Pre dic tion
WANG Qi-di,JIN Xin-qiao,DU Zhi-min,ZHU Yong-hua
Institute of Refrigeration and Cryogenics,Shanghai Jiao Tong University
Optimal control strategy for the VRV-VAV combining air conditioning system was proposed,and the energy saving operation was realized by changing the supply air temperature set point.The adaptive recursive method and time series analysis method were adopted to set up the prediction model,and revisions were made for insufficiency of the model.The mean and max errors of the revised model are 0.05%and 0.342%.The energy consumption can be reduced to 6.7%after applying the revised model to the optimal control strategy.
VRV-VAV combining system,variable supply air temperature,energy conservation,optimal control strategy,COP prediction
1003-0344(2015)01-001-6
2013-10-15
晋欣桥(1965~),男,教授,上海交通大学制冷与低温工程研究所;021-34206774;E-mail:xqjin@sjtu.edu.cn
国家自然科学基金(No.50976066)
