低轮FOX64算法的零相关-积分分析

郭 瑞 金晨辉

1 引言

目前，对分组密码算法的攻击方法主要分为：差分密码分析[1]及其推广、线性密码分析[2]及其推广、积分攻击、密钥相关攻击、中间相遇攻击、插值攻击等。其中，差分密码分析和线性密码分析是目前对分组密码算法安全性分析的最重要和最有效的工具。最近，文献[3]提出了零相关线性分析，该分析方法基于相关系数为0的线性逼近，并通常被看作与不可能差分分析相对应的一类推广的线性密码分析方法。

文献[3]提出零相关线性分析方法时，给出了AES算法、Skipjack算法、CAST256算法、CLEFIA算法相关系数为0的线性逼近，并成功攻击了低轮AES-192, AES-256以及CLEFIA-256。但是，为了判断选取的线性逼近的相关系数是否为 0，零相关线性分析需要选取明文规模至少为分组规模一半。因此，攻击所需数据复杂度较高是零相关线性分析最大的缺陷。随后，文献[4]证明了使用多个独立的零相关线性逼近可以降低数据复杂度。但是，多个线性逼近相互独立的假设难以满足。为此，文献[5]指出可以使用不同的已知明文来消除线性逼近互相独立的假设，从而降低攻击所需的数据复杂度，并给出了零相关线性区分器与积分区分器、多维线性区分器的关系。证明了由积分区分器可以得到零相关线性逼近区分器、由零相关线性逼近区分器在一定条件下同样可以得到积分区分器，证明了零相关线性区分器是多维线性区分器的特例。同时，首次给出了变形的31轮Skipjack算法的零相关-积分攻击。此外，文献[6]还给出了LBlock算法的多维-零相关线性分析，且攻击结果的时间复杂度优于已有攻击结果。

本文分析 FOX系列分组密码算法抵抗零相关线性分析的能力。FOX分组密码算法是文献[7]为了满足Mediacrypt公司的需求而设计，包括分组规模为64 bit和128 bit两类算法，通常称为FOX64和FOX128。FOX系列分组密码算法的安全性基于Lai-Massey模型[8,9]的可证明安全结论，其圈函数采用嵌套 SPS结构的 Lai-Massey模型，密钥规模 k满足0256k≤≤，且是8的倍数。特别地，FOX算法使用了复杂的密钥编排算法，使得其由若干子密钥无法获取种子密钥或其它子密钥。已有对FOX算法有效的攻击包括碰撞-积分攻击、不可能差分分析、差分碰撞攻击等。文献[10]利用FOX算法的3轮区分器及碰撞技术对4, 5, 6, 7轮FOX64分析的时间复杂度分别为245.4, 2109.4, 2173.4, 2237.4，数据复杂度为29个选择明文。文献[11]和文献[12]独立地找到了4轮FOX算法的不可能差分对应，并指出不可能差分攻击对5, 6, 7轮FOX64的时间复杂度分别为269, 2133, 2197，攻击的数据复杂度大约为 239个选择明文。此外，文献[13]给出了FOX算法的差分-碰撞攻击，攻击需要的数据复杂度很小，但预处理复杂度较高。文献[14]给出了FOX算法的差错故障分析结果。

本文首先给出了FOX64算法大量4轮零相关线性逼近，然后利用零相关线性逼近区分器与积分区分器的关系，首次得到了FOX64算法4轮积分区分器。最后，利用积分分析方法对 5,6,7,8轮 FOX64进行了攻击。

2 基础知识

本节首先简单介绍 FOX算法及其圈函数线性逼近的一般规律，然后介绍零相关线性分析。

2.1 FOX分组密码算法[7]简述

FOX算法使用的圈函数是嵌套 SPS结构的Lai-Massey模型。限于篇幅，只对FOX64进行详细介绍，FOX128可看作两个 FOX64的并置。FOX64/k中的k是密钥长度。

轮函数 f : {0,1}32×{0,1}64→{0,1}32由字节代替变换sigma4、线性置换mu4和密钥异或加构成，其使用的子密钥K = k0k1是 64 bit，表达式为f( x, K ) = sigma4(mu4(sigma4(x ⊕ k0) ) ⊕ k1)⊕ k0。其中sigma4: {0,1}32→{0,1}32由4个相同的8进8出的 s盒并置而成，扩散层 mu4: [GF(256)]4→[GF(256)]4使用一个分支数为5的MDS矩阵，其定义为

Z = α-1⊕ 1 ,α 是不可约多项式 m ( x ) = x8⊕ x7⊕x6⊕ x5⊕ x4⊕ x3⊕ 1 的一个根。

FOX64算法圈函数迭代16次，64 bit明文P经加密后得到的64 bit密文为

C=Imid64（ Imor64 （ …(Imor64 （ P , K1）,… ,K2）,Kr）其中圈函数 I mor64(xl||xr) =or(xl⊕f32(xl⊕xr,k ))||(yr⊕f32(xl⊕xr,k )),K1, K2,…,Kr是各圈使用的64 bit子密钥，or(x, y ) = ( y, x ⊕ y ) 是圈函数使用的线性正形置换，最后一轮圈函数Imid64无正形置换。

设 FOX算法中使用的正形置换or对应矩阵为M。给出FOX64算法圈函数线性逼近对应的一般规律。

引理1 FOX64算法圈函数Qk的线性逼近(α, β)→ (A, B)的相关系数为非零ρ的充分必要条件是α ⊕ β ⊕ B⊕ M A=0。此时，F函数对应的线性逼近为 β ⊕ B → α ⊕ β 且满足相关系数也是 ρ 。

证明 设 ( x1,x2)为 Qk的输入，令 x =x1,y = x1⊕x2，将x, y看作列向量，则有

本 文 记 Δ=α ⊕ β ⊕ B⊕MTA , Γ( y ) = (MTA⊕B ) ⋅ F (y ) ⊕ (β ⊕ B)⋅y 。则有

F F特别地，由于正形置换or满足 MT=M ，可得α ⊕ β ⊕ B⊕ M A=0。充分条件显然。 证毕

此外，FOX算法使用的正形置换or(x, y)=(y, x ⊕y)及逆置换io(x, y ) = ( x ⊕ y , x)具有的性质为：

性质 1[7](1) or2(x, y ) = i o(x, y), io2(x, y)=or(x, y ) ; (2)io(x, y ) ⊕ o r(x, y ) ⊕ (x, y ) = (0,0); (3)or(x, y ) = ( x, y)当且仅当(x, y) = ( 0,0); (4) o r3(x, y)= ( x, y)。

2.2 零相关线性逼近[15]

定义 1[2]给定函数 F = fr-1°…° f0的一个线性堆 α → β ，称 Γ = ( α0, α1, … ,αr) 为F函数的一个起点为α=α0，终点为β=αr的组合传递链。设线性堆 α → β 的相关系数为 CF(α, β) , fi的线性特征(αi-1,αi) 的 相 关 系 数 为 Cfi( αi-1,αi)， 则 有CF(α, β) = Cf1(α0, α1) Cf2(α1, α2) … Cfr(αr-1,αr)。

定义 2[2]给定函数 F =° f °…° f，设 r-20Γ = ( α0, α1, … ,αr) 为F函数的一条组合传递链，如果圈函数 fi的线性逼近 αi→ αi+1的相关系数Cfi(αi, αi+1) = 0，则称线性选择模式对 (αi, αi+1)是不相容的。

由此，文献[3]给出了零相关线性逼近存在的充分条件为：

引理 2[3]给定函数 F =° f °…° f，设 r -20α → β为F函数的一个线性堆对应，如果该线性堆的任意一条组合传递链 Γ = ( α, α1, L,αr-2,β)至少存在一对不相容的选择模式对，则 CF(α, β) = 0。

此外，本文给出如下几个引理和定义：

引理 3[3]对于置换P，其相关系数非零的充分条件是输入、输出选择模式都为零或者都不为零。

定义3[2]如果 X = (x0, x1, … , xn-1) ∈ ()n，则称wt(X) = # {0 ≤ i ≤ n - 1 : xi≠0}为X的重量。

定义 4[2]设线性变换 L ( x ) =Ax，则线性分支数定义为 Bl= m in{wt(ATΓ y ) + w t(Γ y ) : Γ y ≠0}，其中 AT表示矩阵A的转置。

2.3 零相关-积分分析

文献[5]研究了零相关线性区分器与积分区分器的关系，并将由零相关线性区分器得到积分区分器，然后利用积分区分器攻击分组密码算法的分析方法称为零相关-积分分析。本文进一步研究两类区分器的关系：

引理4[16]设,ξ η均是二元随机变量，且ξ服从等概分布，则ξη⊕服从等概分布的充分必要条件是ξ与η独立。

引理 5[16]设 ξ1, ξ2,… ,ξm和 η1, η2,…,ηn都是二元随机变量，则 (ξ1, ξ2,… ,ξm)与(η1, η2,… ,ηn)独立等价于对所有二元非零向量 (a1, a2,… ,am)和(b1, b2,…,bm),a1ξ1⊕ a2ξ2⊕ … ⊕amξm与b1η1⊕b2η2⊕ … ⊕bnηn均独立。

证明 由于任意非零的 a , b, c, d∈F28，有α⋅x⊕β ⋅ f (x)的 相 关 系 数 为 零 ， 即 [a ⋅ (x1⊕ x3) ⊕ b ⋅ (x2⊕x4)]⊕ [c ⋅ (y1⊕ y3) ⊕ d ⋅ (y2⊕ y4)]为平衡函数，所以(x1⊕ x3, x2⊕ x4)是平衡函数，故由引理4知上式等价 于 a ⋅ (x1⊕ x3) ⊕ b ⋅ (x2⊕ x4)与 c ⋅ (y1⊕ y3) ⊕ d ⋅ (y2⊕y4)独立，再由引理 5可知 ( x1⊕ x3,x2⊕x4)与(y1⊕ y3, y2⊕ y4)独立。所以对任意给定的常值λ1, λ2，加密形如 (x1, x2, x1⊕ λ1, x2⊕ λ2, x3x4x5x6)的所有可能输入， (y1⊕ y3, y2⊕ y4)每个可能值出现的次数是相同的。 证毕

其中 α =(a bab,0000)和 β =(c dcd,0000)最后位置都为0，只是为了形式简单而为之。

3 低轮FOX64算法的零相关线性分析

3.1 4轮FOX算法零相关线性区分器

定理 1 如 果 α ∈{0,1}32{0}且wt(α)+wt(α ⊕ β ) ≤ 4，则(io(α) , io(α) ) → (io(β ) ,io(β))是4轮FOX64(最后一轮无正形置换)的零相关线性区分器。

证明 如图1所示，当输入选择模式为(io(α),io(α))时，设第1轮圈函数的输出选择模式为(A ,B )，由引理1可知io(α) ⊕ i o(α) ⊕ B⊕ M A=0，即A = M-1B，且 f1的输入选择模式和输出选择模式分别为io(α)⊕B和io(α) ⊕ i o(α) =0。再由引理3可知，f1输出选择模式为0，相关系数非零的输入选择模式必为0，即io(α) ⊕ B =0，得 B = io(α)，由此可得 A = or(α)，即第 2圈的输入选择模式为(or(α) , io(α) ) 。对第2轮圈函数使用引理1，得 f2的输出选择模式为or(α) ⊕io(α) =α。假设 f2的输入选择模式为b，由引理1可得第2圈的输出选择模式为(α ⊕io(b ) ,io(α) ⊕ b)。

图 1 4轮FOX64的零相关线性区分器

当第4圈输出选择模式为(io(β) ,io(β) )时，可知第4圈的输入选择模式为(io(β ) ,io(β ) )。此时，对第3轮圈函数使用引理 1有 α ⊕ i o(b ) ⊕ i o(α)⊕b⊕io(β) ⊕ β = 0， 可 得or(b ) = o r(α ⊕ β)， 即 b =α ⊕ β。因此， f2的输入选择模式和输出选择模式分别为α⊕β和α。故当wt(α) + w t(α ⊕ β ) ≤4时，α ⊕ β → α 是 不 相 容 的 。 所 以(io(α),io(α))→(io(β) ,io(β ) )是4轮FOX64的零相关线性区分器。证毕

推论1 对于任意非零字节 a, b, c, d, 4轮FOX64算法具有3类零相关线性区分器：

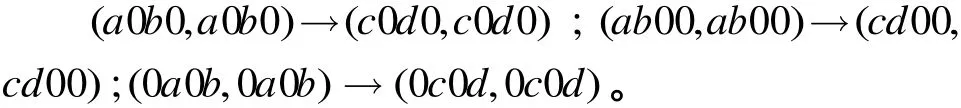
证明 当4轮FOX64算法的输入选择模式和输出选择模式分别为(a0 b 0,a0 b 0 )和(c0 d 0 ,c0 d 0 )时，有wt(or(a0 b 0 )) + wt(or(a0 b 0 ) ⊕ or(c0 d 0)) = 2 + 2 = 4 成立，由定理1可知(a0 b 0 ,a0 b 0 ) → (c0 d 0 ,c0 d 0)为4轮FOX64算法的零相关线性逼近。同理可证另外两种情况。 证毕

3.2 低轮FOX64的零相关-积分分析

本节将利用上节给出的4轮FOX的零相关线性区分器构造4轮积分区分器，同时对低轮的FOX64算法进行零相关-积分分析。为此，首先给出引理7。

引理 7 对于 4轮 FOX64(最后一轮无正形置换)，设4轮FOX64的输出为 (w1w2w3w4, w5w6w7w8)，则

(1)加密 248个所有可能明文 ( p1p2p3p4, p1p5p3p6),w1⊕w5, w3⊕w7的28个可能值各出现 240次；

(2)加密 248个所有可能明文 (p1p2p3p4, p5p2p6p4),w2⊕w6, w4⊕w8的28个可能值各出现 240次；

(3)加密 248个所有可能明文 (p1p2p3p4, p1p2p5p6),w1⊕w5, w2⊕w6的28个可能值各出现 240次。

证明 (1)由推论 1可知(a0 b 0,a0 b 0) → (c0 d 0,c0 d 0 )为4轮FOX64算法的零相关线性逼近，然后取引理6中的λ=0，即可得此结论。同理可得到引理7(2)和引理7(3)。 证毕

下面证明中，令明文结构 P1={(p1p2p3p4,p1p5p3p6) | pi∈F28,i =1,2,… ,6},P2={(p1p2p3p4,p5p2p6p4) | pi∈F28,i =1,2,… ,6},P3={(p1p2p3p4,p1p2p5p6) | pi∈F28,i =1,2,… ,6}。

设第 5轮 64 bit子密钥为 R K5=||, 5轮FOX64(最后一轮无or变换)的输出为 (CL, CR) = (u1u2u3u4, u5u6u7u8)。其中，对于第5轮的Imid64变换，输入块的异或和等于输出块的异或和。所以第5轮F函数的输入为CL⊕CR。

引理8 对于5轮FOX64(最后一轮无or变换)，第4轮的输出 (w1w2w3w4, w5w6w7w8)(未经过or变换)与密文 (CL, CR) = (u1u2u3u4, u5u6u7u8)及 64 bit密钥RK5=的关系为：

其 中(t1t2t3t4) =mu4(sigma4(CL⊕ CR⊕)),( tj)=s[mu4(sigma4(ΔC ⊕⊕]。

证明 由 于 f5( CL⊕CR, RK5) = sigma4(mu4⋅(sigma4(CL⊕ CR⊕⊕⊕，所以已知及 CL⊕CR的值，即可求得(t1t2t3t4) = mu4(sigma4⋅(CL⊕ CR⊕))的值。此时，有

所 以 w1⊕ w5=w1⊕w3⊕w3⊕ w5=u1⊕u3⊕u5⊕(t)⊕，同理可证其它等式。 证毕3

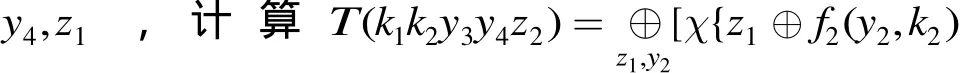
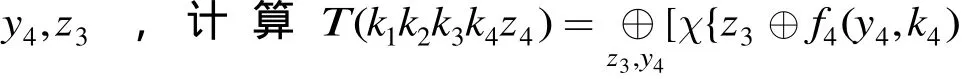
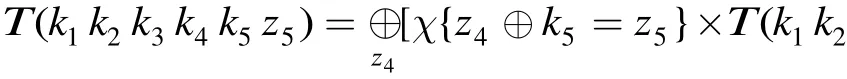
步骤1的时间复杂度为 248× 28= 256，空间复杂度为232。步骤2到步骤5的时间复杂度均为 248，空间复杂度分别为224, 216, 28, 1。故算法1的时间复杂度约为 256，空间复杂度为232。

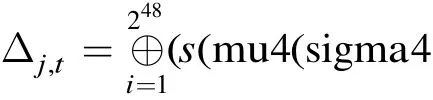
图 2 5轮FOX64的零相关-积分分析

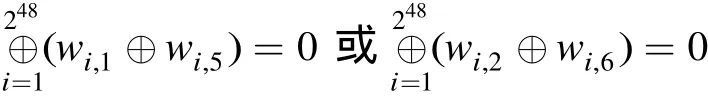
同理，利用引理 7(1)、引理 7(3)，通过统计w3⊕w7和w4⊕w8的28个可能值是否出现 240次，可以分别恢复及，时间复杂度都为 256次查表。故恢复 R K5的数据复杂度为 250个选择明文，时间复杂度为 8 × 256= 259次查表运算。由于FOX64算法圈函数的实现大约需要 24次查表运算。故该攻击的时 间复 杂 度 约 为 259× 2-4× 1 /5 ≈ 252.7次5轮FOX64加密。获得第5轮圈子密钥 R K5后，我们可以利用文献[9]给出的4轮FOX64的积分攻击恢复前4轮子密钥，其复杂度约为 245.4次4轮FOX64加密。此外，对于6轮FOX64的攻击，我们可以通过穷举第6轮全部64 bit子密钥来实现，其时间复杂度约为 2116.7次6轮FOX64加密。同理可知，对7轮和8轮FOX64攻击的时间复杂度约为 2180.7和2244.7次加密。

4 结束语

本文分析了 FOX64算法抗零相关线性分析的能力，并利用零相关线性分析与积分分析相结合的方法分析了FOX64算法的安全性，结果表明零相关-积分分析对低轮FOX64算法是一类有效的攻击。攻击的数据复杂度为 250个选择明文，攻击 5轮FOX64/64的时间复杂度为 252.7次加密，6轮FOX64/128的时间复杂度为 2116.7次加密，7轮FOX64/192的时间复杂度为 2180.7次加密，8轮FOX64/256的时间复杂度为2244.7次加密。鉴于本文关于低轮FOX64的零相关-积分分析结果，要求设计者在设计分组密码算法时，必须评估其抵抗零相关线性分析的能力。

[1] Biham E and Shamir A. Differential cryptanalysis of DES-like cryptosystems[C]. Proceedings of the CRYPTO 1990, Santa Barbara, CA, USA, 1990, 537: 2-21.

[2] Matsui M. Linear cryptanalysis method for DES cipher[C].Proceedings of the EUROCRYPT 1993, Lofthus, Norway,1993, 765: 386-397.

[3] Bogdanov A and Rijmen V. Linear hulls with correlation zero and linear cryptanalysis of block ciphers[J]. Designs, Codes and Cryptography, 2014, 70(3): 369-383.

[4] Bogdanov A and Wang M. Zero correlation linear cryptanalysis with reduced data complexity[C]. Proceedings of the Fast Software Encryption 2012, Washington DC, USA,2012, 7549: 29-48.

[5] Bogdanov A, Leander G, Nyberg K, et al.. Integral and multidimensional linear distinguishers with correlation zero[C]. Proceedings of the ASIACRYPT 2012, Beijing,China, 2012, 7658: 244-261.

[6] Hadi S. Zero correlation linear cryptanalysis of reduced-round LBlock[J]. Designs, Codes and Cryptography,2014, To be published.

[7] Junod P and Vaudenay S. FOX: a new family of block ciphers[C]. Proceedings of the Selected Areas in Cryptography-SAC 2004, Ottawa, Canada, 2004, 2595:131-146.

[8] Vaudenay S. On the Lai-Massey scheme[C]. Proceedings of the ASIACRYPT 1999, Singapore, 1999, 1716: 8-19.

[9] Aaram Y and Je H. On Lai-Massey and quasi-Feistel ciphers[J]. Design, Codes and Cryptography, 2011, 58(1):45-72.

[10] Wu Wen-ling, Zhang Wen-tao, and Feng Deng-guo. Integral cryptanalysis of reduced FOX block cipher[C]. Proceedings of the Information Security and Cryptology-ICISC 2005, Beijing,China, 2005, 3935: 229-241.

[11] Wu Zhong-ming, Lai Xue-jia, Zhu Bo, et al.. Impossible differential cryptanalysis of FOX[C]. Proceedings of the first International Conference on Information Security: Beijing,China, 2010, 6163: 236-249.

[12] 魏悦川, 孙兵, 李超. FOX密码的不可能差分攻击[J]. 通信学报, 2010, 31(9): 24-29.Wei Yue-chuan, Sun Bing, and Li Chao. Impossible differential attack on FOX[J]. Journal on Communications,2010, 31(9): 24-29.

[13] Chen jie, Hu Yu-pu, Zhang Yue-yu, et al.. Differential collision attack on reduced FOX block cipher[J]. China Communications, 2012, 9(7): 71-76.

[14] Li Rui-lin, You Jian-xiong, Sun Bing, et al.. Fault analysis study of the block cipher FOX64[J]. Multimedia Tools and Applications, 2013, 63(3): 691-708.

[15] Blondeau C and Nyberg K. New links between differential and linear cryptanalysis[C]. Proceedings of the EUROCRYPT 2013, Athens, Greece, 2013, 788: 388-404.

[16] 金晨辉. 有限域和剩余类环上非奇异反馈多项式的谱刻划[J].通信学报, 2000, 21(1): 74-77.Jin Chen-hui. Spectra characterizations of nonsingular feedback polynomials over finite fields and residue class rings[J]. Journal of China Institute of Communications, 2000,21(1): 74-77.

[17] Ferguson N, Kelsey J, Lucks S, et al.. Improved cryptanalysis of Rijndael[C]. Proceedings of the Fast Software Encryption 2000, New York, USA, 1978: 213-230.