相位响应固定幅度响应约束的稳健波束形成方法
2015-07-18虞泓波冯大政
虞泓波 冯大政 解 虎
(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
相位响应固定幅度响应约束的稳健波束形成方法
虞泓波*冯大政 解 虎
(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
传统的幅度约束波束形成器是一个非凸问题,需将原始模型化为线性规划进行间接求解。该文针对均匀线阵提出一种相位响应固定幅度响应约束(PFMC)的稳健波束形成方法。利用权矢量逆序列对应的传递函数与阵列响应函数只差一个相位因子这一性质,将阵列响应的相位设置为固定的线性相位,仅对阵列响应的实数幅度进行约束,从而得到一个凸的代价函数,最优权矢量可以利用内点法求出。同时考虑到协方差矩阵误差,利用最坏(WC)情况性能最优原理提出PFMC-WC算法改善PFMC的性能。与传统幅度约束波束形成器相比,减少了约束个数并省掉了恢复权矢量过程,从而降低了计算量。此外,由于相位响应得到保证,该文算法相对于传统算法具有更好的性能。仿真实验验证了该文算法的有效性。
阵列信号处理;稳健波束形成;相位响应固定幅度响应约束;最坏情况性能最优
OI:10.11999/JEIT141513
1 引言
自适应波束形成是阵列信号处理中一项重要任务[1]。近些年来,为了提高波束形成器抗导向矢量误差的性能,人们提出了一些稳健的波束形成方法。2003年Vorobyov等人[2]提出了基于最坏情况的稳健自适应波束形成方法,Li等人[3]提出基于不确定集的导向矢量的估计方法。2008年 Vorobyov等人[4]又提出了基于概率约束的稳健自适应波束形成方法,该方法认为文献[2]中最坏情况以一定的概率出现。文献[2-4]中方法都归属于扩展的对角加载方法。Hassanien等人[5]基于导向矢量失配模型提出一种迭代求解算法以估计期望信号导向矢量。Khabbazibasmenj等人[6]对文献[5]中算法进行改进,提出一种半正定松弛(SDR)算法进行导向矢量估计,与文献[5]中算法相比增大了系统自由度,具有更高的输出信干噪比(SINR)。文献[7]和文献[8]提出了基于协方差矩阵重构的稳健波束形成方法,通过重构干扰和噪声协方差矩阵提高了协方差矩阵的有效性,但这类算法目前计算量很大,需要进一步研究降低计算量的方法。虽然上述方法都在尽力提高波束形成器的稳健性,但是大部分方法均不能灵活控制期望信号所在的稳健区域的宽度和波动程度。近年来,基于幅度响应约束的波束形成方法[912]-被提出,该方法通过对给定角域内的阵列响应幅度上下限强加约束,达到对稳健区域的宽度和波动程度的控制。
本文针对均匀线阵提出一种相位响应固定幅度响应约束的稳健波束形成方法,通过分析发现阵列响应函数与权矢量逆序列的传递函数只差一个相位因子,令权矢量逆序列的传递函数具有线性相位,从而使得阵列响应函数也具有线性固定相位,因此,只需对阵列响应的实数幅度进行约束即可有效控制稳健区域的宽度和波动程度。所提模型为一个凸问题,利用高效的内点法容易求解,与文献[9]和文献[12]中算法相比,能有效提高计算效率。此外,由于将相位响应固定为线性相位,使得相位响应得到保证,与传统幅度约束波束形成器相比,所提波束形成器性能更优,仿真实验表明本文方法对加载因子敏感性更低、样本收敛性更快,并具有更好的抗阵元幅相误差稳健性,从而本文方法更适用于工程应用。
2 相位响应固定幅度响应约束的稳健波束形成方法
2.1 问题模型
假设一个ULA包含N个阵元,阵元间距为d,目标及干扰均为窄带信号,令 x (t)∈CN×1表示阵列接收数据矢量,则最小方差无畸变响应(MVDR)波束形成器可以表示为


θt为目标信号波达方向,为波长。在实际应用中,通常由采样协方差矩阵来估计数据协方差矩阵,其中L为样本数。为了使得滤波器权矢量在一定的角域范围内维持平稳的增益,基于幅度响应约束的稳健波束形成方法被提出[9-13]:

其中 ()L θ与 ()U θ分别表示幅度响应的下界、上界,Θm表示期望的稳健角域。显然,由于存在非凸约束式(3)所示代价函数是一个非凸的问题,难以直接求解。文献[9]通过利用权矢量的自相关函数将式(3)转化为凸问题,再利用谱分解方法求解权矢量,求解过程较为繁琐且最优解受谱分解方法的影响。文献[12]采用迭代 SOCP算法进行求解以逼近原始问题的最优解,虽然文献[12]说明了迭代 SOCP求解式(3)的有效性,但是迭代求解子SOCP问题的方法大大降低了计算效率,不利于快速计算。文献[14,15]等提出稳健线性约束最小方差(LCMV)波束形成器及和差波束形成器,探索了波束形成器的相位响应,这启发我们研究传统幅度约束波束形成器的相位响应。
2.2 相位响应固定幅度响应约束方法(PFMC)


其中符号*表示卷积。假设输入序列为N点,那么在 1N- 时刻的输出为

对比式(4)与式(6),可以发现阵列响应函数相当于输入序列经过一个单位脉冲响应序列为的系统后在 N- 1时刻的输出,如图 1所示。图中N-1 。将阵列响应函数进一步转化:


图 1 输入输出过程示意图


观察式(9)可知,固定的阵列响应函数的相位为

这样,阵列响应函数可以表示为实数幅度特性与相位特性的乘积:


由于 Hm(ejΩ)是实数,这里令其非负。根据式(12),可以将式(3)改写为

容易看出,式(13)所示约束是凸的。这样一个新的稳健模型可以表示为

虚部为零的约束可以省去,这是由于式(14)中的约束已经隐含了是实数。显然式(14)为一个凸优化问题,约束部分可以在角域mΘ 内通过角度采样进行近似[912]-。这样式(14)所示代价函数即可用高效的内点法进行求解。关于代价函数式(14)有如下推论。
推论 如果权矢量逆序列的传递函数 H(ejΩ)采用形如 φ( Ω )= -( N - 1)Ω/ 2+ Ω0(Ω0为任意常数)的固定线性相位,那么其对于式(14)所示代价函数是等效的。
证明 (1)假设式(14)的最优解为optw ,令1=w(相位旋转),则
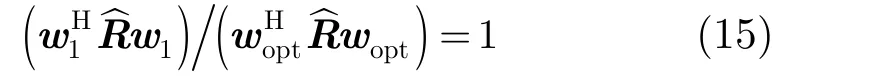
即1w与代价函数式(14)的最优解等效(目标函数值相等),令angle{}·表示取相位,则可以得到。从而

由式(9)可得,权矢量逆序列的传递函数的相位为

(2)若采用线性相位 φ( Ω )= -( N - 1)Ω/ 2+ Ω0,式(3)所示代价函数可以转化为

类似于(1),容易证明其最优解经过相位旋转后(令

由推论可知,采用式(8b)所示线性相位对于本文算法是等效的。
2.3 最坏情况性能最优算法(PFMC-WC)
通常由于样本数不足、阵列先验信息不准确等原因,采样协方差矩阵︿R与真实的协方差矩阵R存在偏差,这种失配模型可以表示为[12]

其中失配量Δ的Frobenius范数被一个已知常数限定,

其中I为N阶单位矩阵。容易看出式(21)为一个凸优化问题,利用高效的内点法容易求解。
3 计算效率分析
比较PFMC与PFMC-WC算法,可以发现两者的区别在于PFMC-WC算法相对于PFMC算法在目标函数中多了一个正则项,因此,对本文方法计算复杂度的分析只需分析式(21)即可。我们将本文方法与文献[9],文献[12]中的方法进行对比,假设所有方法中对角域mΘ 的采样点数均为K,那么本文方法共有2K个线性约束,利用内点法求解每次迭代的计算复杂度为 O( N3+ 2K N2);而文献[9]中的凸问题有3K N+ 个线性约束,利用内点法求解每次迭代的计算复杂度为此外还需要利用基于FFT的谱分解方法恢复权矢量,其计算量为 O( N log N )[9];文献[12]采用迭代求解子SOCP问题(Iterative-SOCP)进行求解,求解每个子SOCP问题的计算复杂度为表1给出了3种算法的计算效率比较。文献[12]指出迭代求解子SOCP问题需要5步以上[12],而用内点法求解本文方法与文献[9]方法一般需要迭代10步左右[2]。从表1可以看出,与文献[9]相比,本文方法可以减少线性约束的个数,并省掉利用谱分解方法恢复权矢量的过程;与文献[12]相比,本文方法只需求解一个二阶凸优化问题,而文献[12]获得权矢量需求解的SOCP问题在5个以上,因此本文方法有效提高了计算效率。综合来看,与文献[9],文献[12]相比,本文方法具有更高的计算效率,更利于实际工程应用。
4 仿真实验与性能分析
假设一个由10个阵元组成的ULA,阵元间距均为半个波长。空间远场处存在两个干扰,方向分别为 30- °,50°,干噪比(INR)均为30 dB。假定的目标信号方向为3°,而真实的目标信号方向为 3-°。阵列响应幅度的上下限分别根据公式 U(θ) =10rdb/20,
给出,其中 rdb(单位为dB)为稳健区域波动程度。为了与本文方法进行对比,还考虑了最优波束形成器,文献[9]方法,文献[12]中Iterative-SOCP算法,Worst-Case算法[2],以及对角加载算法(LSMI)。Worst-Case算法的误差界选取ε= 3[2],LSMI算法的加载水平为10倍噪声功率。除实验1与实验3外,其余实验均为100次实验取平均值的结果。
实验1 比较不同算法的阵列响应函数的相位
假定信噪比SNR=10 dB,样本数为200。本文方法选取波束宽度15°,选取 6γ= (本文实验中γ的数值均为噪声功率的倍数),波动因子 rdb= 0.2 dB ,角域范围为[-7:0.2:8]°,在[- 7°,8°]内以0.2°为间隔进行采样。
图2给出了5种算法在[-7°,8°]范围内的阵列相位响应特性,从图中可以看出,最优波束形成器的相位响应曲线在角域范围内为一条直线,而文献[9]中方法及Iterative-SOCP算法在角域范围内的相位响应曲线有所弯曲,且曲线斜率与最优相位响应曲线有较大偏差。本文方法在角域范围内相位响应曲线为一条直线,且斜率与最优响应曲线几乎相等。图2说明了本文将阵列响应函数设定为线性相位的有效性。
实验 2 观察本文算法性能随加载因子γ的变化情况
假设波束宽度为20°,稳健角域选为[-1 0°,10°],波动因子 rdb= 0.2dB,加入Iterative-SOCP文献[9]中算法与本文算法进行对比。图3给出了3种算法在SNR=10 dB时样本数为100时输出SINR随加载因子γ的变化。从图3可以看出,本文方法在低加载量时输出SINR与高加载量时输出SINR相差较小,而Iterative-SOCP文献[9]方法低加载量时输出SINR与高加载量时输出SINR相差较大,这说明本文方法对加载量的敏感性小于 Iterative-SOCP与文献[9]方法。

表1 计算效率对比

图2 相位特性

图3 输出SINR随加载因子γ的变化曲线
实验 3 观察本文方法对稳健区域的宽度和波动程度的控制能力
样本数为200,选取 6γ= ,分别考虑在确定的波动因子下不同稳健区域宽度,以及在确定稳健区域宽度下不同波动因子时的波束方向图(说明:图4(c)、图4(d)分别为图4(a)、图4(b)的局部放大图)。
图4给出了在不同稳健区域宽度和波动程度下本文方法的波形图。从图4(a)和图4(b)中可以看出,波形图的稳健区域和波动程度与所设置的参数相匹配,这说明本文方法能够灵活控制波束宽度和波动程度。同时,所有波形图在干扰方向均形成零限,意味着对干扰有较好的抑制能力。
实验4 观察算法的输出SINR与样本收敛性将本文算法的协方差矩阵加载因子γ设置为γ= 6,波动因子 rdb= 0.2 dB,波束宽度为20°。为了公平比较,文献[9]与文献[12]中算法设置为同样的参数。
图5给出了样本数为200时输出SINR随输入SNR变化曲线,从图中可以看出在低SNR区域本文PFMC-WC算法与Iterative-SOCP和文献[9]中算法的输出SINR相当,在15 dB到20 dB的SNR区域,本文PFMC-WC算法有着更高的输出SINR。图6给出了在SNR=10 dB时输出SINR随样本数变化曲线,样本数从10开始,从图6可以看出,在小样本情形,本文算法相对于Iterative-SOCP和文献[9]算法输出SINR更高,这说明本文算法有着更快的样本收敛性。
实验5 观察阵元幅相误差对本文算法的影响
在实际应用中,由于阵元尺寸、位置等误差,会造成阵列导向矢量存在幅相误差。本文 PFMCWC算法、Iterative-SOCP与文献[9]算法中的参数设置如同实验4,样本数为200。假设各阵元存在服从高斯分布的随机幅相误差,图7给出了SNR=10 dB时5种算法随阵元幅相误差方差的变化曲线。

图4 本文方法对稳健区域宽度和波动程度控制

图5 输出SINR随输入SNR变化曲线

图6 输出SINR随样本数变化曲线

图7 输出SINR随阵元幅相误差的方差变化曲线
从仿真实验可以看出,本文方法能灵活控制稳健区域的宽度和波动程度,且与传统幅度约束波束形成器相比,对加载因子敏感性更低、样本收敛性更快、具有更好的抗阵元幅相误差稳健性。这是由于对于均匀线阵,其导向矢量的空域角频率类似于时域离散信号的频率,本文在设计相位响应时,将波束形成过程类比到时域离散系统的FIR滤波器设计,因此本文方法本质上是传统幅度约束波束形成器与FIR滤波器的结合,通过人为固定线性相位响应,使得相位响应得到保证,而传统幅度约束波束形成器仅对幅度响应进行约束但没有考虑相位响应,故不能保证得到足够好的相位响应(实验1也验证了这一点),因此本文方法相对于传统算法具有更好的性能。
5 结束语
本文针对均匀线阵的特性,将其阵列响应函数的相位设置为固定线性相位,通过对角域内的实数幅度进行约束构建稳健PFMC模型。本文方法无需模型转化,与传统幅度约束波束形成器相比减少了线性约束个数,省去了谱分解方法恢复权矢量的过程,进一步减小了计算量,更利于工程应用。本文提出的PFMC-WC进一步改善PFMC的性能。仿真实验表明,在线性相位保证下,本文方法能灵活控制稳健区域的波束宽度和波动程度,对加载因子敏感性低,样本收敛速度更快,且对阵元幅相误差也有较好的稳健性。
[1] Van Trees H L. Detection,Estimation,and Modulation Theory,Part IV:Optimum Array Processing[M]. New York:Wiley,2002:439-452.
[2] Vorobyov S A,Gershman A B,and Luo Z Q. Robust adaptive beamforming using worst-case performance optimization:a solution to the signal mismatch problem[J]. IEEE Transactions on Signal Processing,2003,51(2):313-324.
[3] Li J,Stoica P,and Wang Z. On robust capon beamforming and diagonal loading[J]. IEEE Transactions on Signal Processing,2003,51(7):1702-1715.
[4] Vorobyov S A,Chen H,and Gershman B. On the relationship between robust minimum variance beamformers with probabilistic and worst-case distortionless response of constraints [J]. IEEE Transactions on Signal Processing,2008,56(11):5719-5724.
[5] Hassanien A,Vorobyov S A,and Wong K M. Robust adaptive beamforming using sequential quadratic programming:an iterative solution to the mismatch problem[J]. IEEE Signal Processing Letters,2008(15):733-736.
[6] Khabbazibasmenj A,Vorobyov S A,and Aboulnasr H. Robust adaptive beamforming based on steering vector estimation with as little as possible prior information[J]. IEEE Transactions on Signal Processing,2012:60(6):2974-2978.
[7] Gu Y,Goodman N A,Hong S H,et al.. Robust adaptive beamforming based on interference covariance matrix sparse reconstruction[J]. Signal Processing,2014,96(B):375-381.
[8] Li J,Wei G,and Ding Y. Adaptive beamforming based on covariance matrix reconstruction by exploiting interferences' cyclostationarity[J]. Signal Processing, 2013, 93(9):2543-2547.
[9] Zhu L Y,Ser W,Er M H,et al.. Robust adaptive beamformers based on worst-case optimization and constraints on magnitude response[J]. IEEE Transactions on Signal Processing,2009,57(7):2615-2628.
[10] Zhang T T and Ser W. Robust beampattern synthesis forantenna arrays with mutual coupling effect[J]. IEEE Transactions on Antennas and Propagation,2011,59(8):2889-2895.
[11] Xu D J,He R,and Shen F. Robust beamforming with magnitude response constraints and conjugate symmetric constraint[J]. IEEE Communications Letters,2013,17(3):561-564.
[12] Liao B,Tsui K M,and Chan S C. Robust beamforming with magnitude response constraints using iterative second-order cone programming[J]. IEEE Transactions on Antennas and Propagation,2012,60(9):3477-3482.
[13] Zhu L Y,Er M H,Ser W,et al.. Spectral factorization for integer-interval sampled sequence with applications in array processing[J]. Signal Processing,2008,88(7):1715-1724.
[14] Xu J W,Liao G S,and Zhu S Q. Robust LCMV beamformer based on phase response constraint[J]. Electronics Letters,2012,48(20):1304-1306.
[15] 许京伟,廖桂生,朱圣棋. 基于幅相线性约束的自适应和差波束形成方法[J]. 电子学报,2013,41(9):1724-1729.
Xu Jing-wei,Liao Gui-sheng,and Zhu Sheng-qi. Approach of adaptive sum and difference beamforming based on magnitude and phase linear constraint[J]. Acta Electronica Sinica,2013,41(9):1724-1729.
[16] 胡光书. 数字信号处理:理论. 算法与实现[M]. 北京:清华大学出版社,2012:218-237.
[17] Escobar G,Mattavelli P,Hernandez G M,et al.. Filters with linear-phase properties for repetitive feedback[J]. IEEE Transactions on Industrial Electronics,2014,61(1):405-413.
虞泓波: 男,1988年生,博士生,研究方向为阵列信号处理、空时自适应信号处理.
冯大政: 男,1959年生,教授,博士生导师,研究方向为自适应阵列信号处理、盲信号处理、MIMO雷达信号处理、神经网络等.
解 虎: 男,1987年生,博士生,研究方向为空时自适应信号处理.
Robust Beamforming with Phase Response Fixed and Magnitude Response Constraint
Yu Hong-bo Feng Da-zheng Xie Hu
(National Laboratory of Radar Signal Processing, Xidian University,Xi'an 710071,China)
The conventional magnitude constraints beamformer is a non-convex issue which is reformulated as a linear programming issue. A robust beamformer with Phase response Fixed and Magnitude response Constraint(PFMC) is proposed for Uniform Linear Array (ULA). Making use of the property that there is only a phase factor difference between the transfer function of the inverse sequence of the weight vector and the array response function,the phase response is set to be linear and the real magnitude response is constrained. Thus,a convex optimization cost function is established whose optimal solution can be found out by highly efficient interior point method. The PFMC-WC method against covariance matrix error is proposed based on Worst Case (WC)performance optimization to improve the performance of PFMC. Compared with the conventional magnitude response constraint beamformer,the proposed method reduces the number of constraints and leaves out the processing of recovering the weight vector,therefore,the calculation cost is reduced. In addition,due to the guarantee of the phase response,the proposed beamformer has better performance than the traditional magnitude constraint beamformer. Simulation results demonstrate the effectiveness of the proposed beamformer.
Array signal processing;Robust beamformer;Phase response Fixed and Magnitude response Constraint (PFMC);Worst-Case (WC) performance optimization
TN911.7
A
1009-5896(2015)07-1688-07 D
2014-11-27收到,2015-03-11改回,2015-06-01网络优先出版
国家自然科学基金(61271293)资助课题
*通信作者:虞泓波 beyond_hongbo@126.com
