基于抽样流长与完全抽样阈值的异常流自适应抽样算法

伊 鹏 钱 坤 黄万伟 王 晶 张 震

（国家数字程控交换系统工程技术研究中心 郑州 450002）

基于抽样流长与完全抽样阈值的异常流自适应抽样算法

伊 鹏 钱 坤*黄万伟 王 晶 张 震

（国家数字程控交换系统工程技术研究中心 郑州 450002）

高速IP网络的流量测量与异常检测是网络测量领域研究的热点。针对目前网络流量测量算法对小流估计精度偏低，对异常流量筛选能力较差的缺陷，该文提出一种基于业务流已抽样长度与完全抽样阈值 S的自适应流抽样算法（AFPT）。AFPT算法根据完全抽样阈值S筛选对异常流量敏感相关的小流，同时根据业务流已抽样长度自适应调整抽样概率。仿真和实验结果表明，AFPT算法的估计误差与理论上界相符，具有较强的异常流量筛选能力，能够有效提高异常检测算法的准确率。

网络测量；自适应流抽样；异常检测

1 引言

网络基础通信设施的大规模部署和网络接入方式的开放性，使得互联网成为一种高度异构与开放的复杂系统［1］。通过网络流量测量技术，可以帮助人们理解掌握网络运行状况，进而优化网络结构和网络应用。网络上的数据报文流经测量节点后，根据系统测量算法必须进行数据压缩［2］或者抽样［3］以减少流量日志，并将测量流量按照一定的数据结构格式存储。测量过程完成后，得到的流量数据可以进一步用于流量分布特征估计、流量计费以及异常检测［4，5］等应用分析。

流量测量时由于大流较小流更容易被抽样检测，因此大流的测量难点主要在于优化数据存储结构或抽样模型，小流由于数量的庞大性和较低的抽样率，与大流的测量估计往往不能兼得［6］。网络研究和管理者仅使用部分原始流量对网络流量的异常检测进行分析，但由于原始流量信息的不完整性使得异常检测算法的分析结果在准确率上不可避免地存在一定偏差［7，8］。针对上述问题，一种理想的流量测量算法首先应当能够为流量分布特征提供较高估计精度信息，同时对异常流量具有准确的筛选抽样能力，或者是具有能够在测量中保留大量与异常流量敏感相关的小流数据的能力。

草图指导的抽样（Sketch Guided Sampling，SGS）算法［9］基本能够解决上述问题，该算法抽样保留每流（per-flow）信息，设置包抽样率为该数据包所属业务流当前流量的单调递减函数。随机共享计数器（Randomized Counter Sharing，RCS）算法［10］是一种较好地满足以上要求的算法，其核心思想是：从流量数据的存储优化出发，使用m组计数器压缩存储所有数据信息，将不同业务流的数据信息随机存储在 l（ 0 ＜ l ＜ m）组计数器内。文献［11］提出了一种基于网络流长分布的自适应抽样（Flow Size Adaptive Sampling，FSAS）算法，FSAS通过估计异常流量的分布特征，得到异常流量的流长阈值，根据阈值对流量进行分段抽样，其自适应抽样的实质是分段的静态流抽样算法。文献［12］提出了一种特征感知的自适应流抽样（Adaptive Flow Sampling，AFS）方法，根据流量五元组特征定义了2个特征矩-特征计数和特征熵，在采样前计算特征矩，在抽样时一旦某一特征值出现频度过高立即降低该业务流的抽样率。

本文针对当前流量测量算法对网络流统计特征估计误差偏高、对异常流量抽样能力偏弱的问题，提出一种基于业务流抽样流长与完全抽样阈值S的自适应流抽样算法（Adaptive Flow sampling algorithm based on sampled Packets and force sampling Threshold S，AFPT）。第2节对AFPT算法的抽样模型给出了详细描述，并从理论上对AFPT算法的流长度无偏估计、标准差以及存储开销进行了分析证明。第3节采用真实链路数据和模拟攻击流量对AFPT算法进行仿真测试，实验结果与第2节的理论分析吻合。第4节总结全文。

2 自适应流抽样算法

2.1 抽样模型

定义1 抽样概率函数 P（ s） =1/（p（ s+ 1）- p（ s）），其中抽样函数 （）p s满足条件：

（2）p（ s）满足 p（ 0）= 0且 p（ 1）= β，β ＞ 0，β可用于调整完全抽样阈值S；

（3）p（ s + 1）＜ α p（ s）+ β，α＞ 1，β ＞0。

2.2 理论分析

定理1 使用AFPT算法抽样时，原始业务流长度n的无偏估计是

证明 对于流长度真实值为n的业务流，若计数器计数值s i= ，有：

令 L（n）表示业务流长度的真实值为n时，无偏估计n（s）的期望值，则

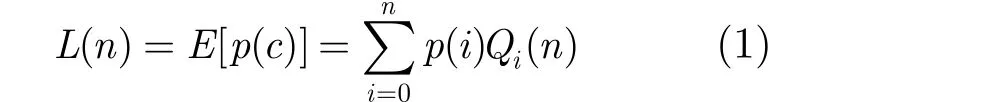
由式（1）可得

根据定义1可得 p（ i + 1）- p（ i） = 1/P（ i ），则有

故

（2）完全抽样阈值 S|β= S0＞ 1时，根据上述推导，得

若n ＞ S0，则

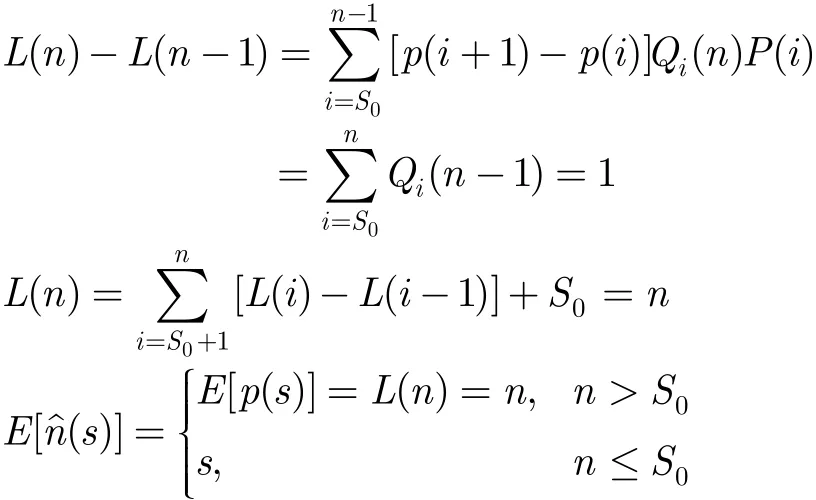
综合上述推导定理1得证。 证毕

证明 对流长度 n ≤ S0的业务流，估计误差始终为0。

对流长度 n ＞ S0的业务流，由 E［ p2（ s） ］=和定义1可得：

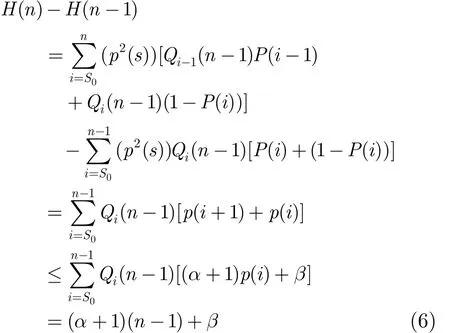
进一步可得：

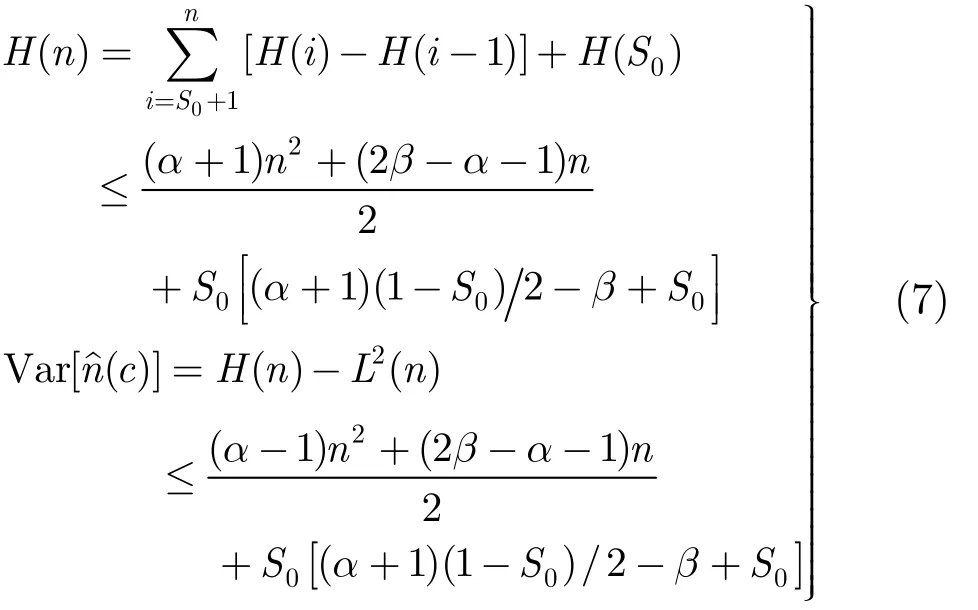
AFPT算法的标准差上界为

证毕

表1是SGS，RCS和AFPT算法的抽样概率函数与理论标准差。图1（a）～图1（c）分别是3种算法的标准差对比。SGS算法和RCS算法的理论误差相近，误差均随流长度的增加而减小，AFPT算法的理论误差随流长度的增加略有增大，但误差最大值仍然小于0.071。

表1 理论误差

2.3 存储开销

抽样算法的主要存储开销集中在流长度计数器的使用上。为尽可能保留原始流量信息，抽样算法通常采用每流抽样模型，为每个业务流创建流长度计数器；在计数器的设计上，由于业务流长度的差异跨度非常大，抽样算法为保证所有业务流的统计需求，必须根据最大业务流长度值确定计数器位宽。

定理3 对真实大小为n的业务流，AFPT算法计数器位宽的数学期望上界是p-1（n），其中p-1（n）是p（c）的反函数。

图1 3种算法的理论误差

证毕

图2对比了SGS算法与AFPT算法所需计数器位宽，对于流长度在100以内的小流，SGS算法和AFPT算法的计数器位宽差距较小。随着业务流长度的增加，SGS算法的计数器位宽成对数比例增加，AFPT算法的计数器位宽趋近于10且此时已能够满足流长度在 107以内的所有业务流。即使在提高完全抽样阈值时，AFPT算法的计数器位宽仍然保持趋近于10，存储开销未出现大幅增加。与RCS算法相比，在小流与中大流计数器位宽的使用上，AFPT算法优于RCS算法，随着流长度的增加，AFPT算法所需的计数器位宽趋近于10略大于RCS算法。

3 仿真与结果分析

3.1 真实网络流量下的仿真实验

本文使用CAIDA［13］在2012年3月10日采集的互联网实际网络40 Gbps链路的流量数据。仿真过程中，SGS算法参数设置为 0.1ε= ，计数器位宽为14；AFPT算法抽样概率β=1 ；RCS算法的计数器组数随机映射计数器数目 100l= ，计数器位宽 8b= 。

AFPT算法抽样仿真结果与标准差如图3所示。对图 3（b）中的标准差数据点进行统计，结果如表 2所示，AFPT的标准差稳定在0.071以内，97.67%的数据点误差范围在 0.071以内，个别小流的标准差稍大于0.07但原始流量的整体误差仍然小于0.5。随着业务流长度的增加，标准差完全落在区间［0，0.071］以内，这与定理2的标准差理论上界保持一致。

表2 3种算法标准差的区间比例

图4是SGS算法的流长度估计值与标准差，估计误差显著高于AFPT算法。尽管大流的估计误差较低，但小流的估计误差是AFPT的数十倍以上。由于SGS使用哈希引入了误判误差，SGS的标准差在0.1以上的比例超过了17.36%，且小流的估计精度差于AFPT，标准差上界较AFPT高出约30%。

RCS算法的流长度估计值与标准差如图 5所示。与SGS相比，RCS对小流的标准差较大，当业务流长度达到100左右时标准差基本稳定在1以内，且快速降低趋近于0。RCS约81.28%的标准差在0.3以内，稍差于SGS。而AFPT仿真结果的标准差仅在0.01以内的比例就高达99.85%，且AFPT算法的标准差基本落在0.071以内，误差上界较RCS降低约76.3%。

图2 报文抽样与AFPT算法需要的计数器位数

图3 AFPT算法仿真结果

图4 SGS算法仿真结果

3.2 异常流量下的仿真实验

在DoS、端口扫描或者蠕虫攻击等网络攻击下会使网络链路产生大量的小流，抽样测量时如果能够对这些小流尽可能地抽样就可以获得更多的异常流量数据，为异常检测算法的准确率提供更加可靠的保证。由于不同类型攻击流的流长并没有相关的明确定义，综合考虑存储资源的消耗，本文选择设置完全抽样阈值 50S= 以满足大多数攻击流都可被抽样，实际阈值的设置视需求而定。

AFPT的抽样概率函数P（s）值取决于α与β，对于不同的取值组合 （）P s可能出现大于1的情况。对P（s）取值大于1的概率点，均以概率1进行完全抽样。若取β∈［0，1］间任意值，可调整完全抽样阈值S，将需要深入研究的业务流全部保留，仅对流长度超过阈值S的业务流进行抽样测量。图 6是 α= 1.01时，完全抽样阈值随β的变化曲线。

图7（a）是SGS，RCS和AFPT这3种算法对合成流量的测量仿真结果，SGS和RCS算法的参数设置与3.1节的仿真实验一致，AFPT算法取完全抽样阈值。异常流量的合成采用文献［14］提出的构造方法，基于实验中使用的正常情况下网络数据流量和DARPA入侵检测流量［15］，模拟异常流量的攻击强度为每秒30000包，其中异常流量比例约20.8%，攻击流量在100 s，200 s，300 s时逐渐达到60%。

SGS的异常流量抽样比例接近于 0.7，最差约0.4。由于 RCS对所有数据报文采用了数据压缩方式存储，对异常流量的抽样原则仅与压缩率有关，比例值稳定在 0.8左右，即使在过渡压缩数据信息时的抽样比例降低至约 0.6，仍优于 SGS。AFPT通过设置完全抽样阈值，抽样比例显著优于SGS和RCS，比例值稳定在1.00左右，在攻击流量较为集中时也能够保证抽样比例不小于 0.75，基本实现对异常流量的逐包抽样统计。

AFPT与AFS，FSAS算法的比较结果如图7（b）所示，其中，FSAS的参数设置为：大中小流阈值分别是1000，500，50，抽样概率分别是0.01，0.10，0.20。由于 FSAS需要在抽样的同时估计业务流长度，极其耗费计算资源，因此在攻击强度增大时，对小流的估计偏差也相应增大，导致其抽样性能下降非常明显。AFS的抽样效果略差于AFPT，这是由于 AFS的特征矩是根据流五元组特征信息定义的，而抽样攻击流量中的Probe与U2R等攻击流仅仅依靠这些特征信息是不够的。

4 结束语

图5 RCS算法仿真结果

图6 完全抽样阈值S的变化曲线

图7 异常流量抽样比例

高速 IP网络的流量测量在抽样与异常检测之间，一直存在由于抽样导致的异常检测偏差。本文提出一种可设置完全抽样阈值的抽样算法，在对网络业务流抽样估计原始流量分布特征的同时，将与异常流量敏感相关的小流完全抽样，使得异常检测处理的流量数据中包含了至少 75%以上的异常流量，有助于提高检测算法的准确率。该算法将抽样流量的估计误差上界降低了30%以上，在存储开销上降低了对计数器位宽的需求，与其他每流测量算法相比所需的存储开销基本持平并未明显增加。通过实验仿真的进一步验证，该算法完全能够适用于40 Gbps速率的骨干链路，对大型骨干网络的管理规划具有重要意义。

［1］ Zhou Ai-ping，Cheng Guang，and Guo Xiao-jun. High-speed network traffic measurement method［J］. Journal of Software，2014，25（1）：135-153.

［2］ Peter Lieven and BjörnScheuermann. High-speed per-flow traffic measurement with probabilistic multiplicity counting［C］. Proceedings of the INFOCOM 2010，San Diego，CA，USA，2010：1-9.

［3］ Cheng Guang and Tang Yong-ning. Estimation algorithms of the flow number from sampled packets on approximate approaches［J］. Journal of Software，2013，24（2）：255-265.

［4］ Lee Y J，Yeh Y R，and Wang Y C F. Anomaly detection via online oversampling principal component analysis［J］. IEEE Transactions on Knowledge and Data Engineering，2013，25（7）：1460-1470.

［5］ Pham D S，Venkatesh S，Lazarescu M，et al.. Anomaly detection in large-scale data stream networks［J］. Data Mining and Knowledge Discovery，2014，28（1）：145-189.

［6］ Cai Yuan-jun，Wu Bin，Zhang Xin-wei，et al.. Flow identification and characteristics mining from internet traffic with hadoop［C］. Proceedings of the Computer Information and Telecommunication Systems （CITS），Jeju Island，Korea，2014：1-5.

［7］ Brauckhoff D，Tellenbach B，Wagner A，et al.. Impact of packet sampling on anomaly detection metrics［C］. Proceedings. of the 6th ACM Sigcomm conference on Internet measurement，Rio de Janeiro，Brazil，2006：159-164.

［8］ Mai Jian-ning，Chuah C N，Sridharan A，et al.. Is sampled data sufficient for anomaly detection？［C］. Proceedings of the 6th ACM Sigcomm Conference on Internet Measurement，Rio de Janeiro，Brazil，2006：165-176.

［9］ Kumar A and Xu J. Sketch guided sampling using on-line estimates of flow size for adaptive data collection［C］. Proceedings of IEEE INFOCOM 2006，Barcelona，Spain，2006：1-11.

［10］ Li Tao and Chen Shi-gang. Per-flow traffic measurement through randomized counter sharing［J］. IEEE ACM Transactions on Networking，2012，13（5）：325-336.

［11］ 王苏南. 高速复杂网络环境下异常流量检测技术研究［D］. ［博士论文］，信息工程大学，2012：38-49.

Wang Su-nan. Research on anomaly detection technology in high-speed complex network environment［D］. ［Ph.D. dissertation］，The PLA Information Engineering University，2012：38-49.

［12］ 郭通. 基于自适应流抽样测量的网络异常检测技术研究［D］.［博士论文］，信息工程大学，2013：38-49.

Guo Tong. Research on network anomaly detection technology based on adaptive flow sampling measurement［D］.［Ph.D. dissertation］，The PLA Information Engineering University，2013：38-49.

［13］ CAIDA. Cooperative as-sociation for internet data analysis［OL］. http：//www.caida.org/data，2012.

［14］ Lakhina A，Crovella M，and Diot C. Mining anomalies using traffic feature distributions［C］. Proceedings of the 5th ACM Sigcomm Conference on Internet Measurement，Philadelphia，PA，USA，2005：217-228.

［15］ MIT Lincoln Laboratory. DARPA Intrusion Detection Evaluation［OL］. http：//www.ll.mit.edu/mission/communications/ist/corpora/ideval/data/index.html，1999.

伊 鹏： 男，1977年生，副教授，博士，研究方向为宽带信息网络.

钱 坤： 男，1990年生，硕士生，研究方向为宽带信息网络、网络测量、异常流检测.

黄万伟： 男，1979年生，讲师，博士，研究方向为宽带信息网络.

王 晶： 女，1980年生，讲师，博士生，研究方向为可重构网络与网络测量技术.

张 震： 男，1985年生，讲师，博士，研究方向为网络测量技术.

Adaptive Flow Sampling Algorithm Based on Sampled Packets and Force Sampling Threshold S Towards Anomaly Detection

Yi Peng Qian Kun Huang Wan-wei Wang Jing Zhang Zhen

（National Digital Switching System Engineering Technological R&D Center， Zhengzhou 450002， China）

The network traffic measurement and anomaly detection for high-speed IP network become the hotspot research of network measurement field. Because the current measurement algorithms have large estimation error for the mice flows and poor performance for the sampling anomaly traffic，an Adaptive Flow sampling algorithm based on the sampled Packets and force sampling Threshold S （AFPT） is proposed. According to the force sampling threshold S，the AFPT is able to sample the mice flows which is sensitive to the anomaly traffic，while adaptive adjustment the probability of sampling based on the sampled packets. The simulation and experimental results show that the estimation error of AFPT is consistent with the theoretical upper bound，and provide better performance for the anomaly traffic sampled. The proposed algorithm can effectively improve the accuracy of anomaly detection algorithm.

Network measurement；Adaptive flow sampling；Anomaly detection

TP393

A

1009-5896（2015）07-1606-06

10.11999/JEIT141379

2014-10-29收到，2015-01-13改回，2015-05-11网络优先出版

国家973计划项目（2012CB315901，2013CB329104）资助课题

*通信作者：钱坤 qiank126@126.com