基于恒功率负荷的牵引供电系统潮流计算

王芳，王晓茹（西南交通大学电气工程学院，成都610031）

基于恒功率负荷的牵引供电系统潮流计算

王芳，王晓茹
（西南交通大学电气工程学院，成都610031）

采用电力系统的潮流迭代算法进行牵引供电系统潮流计算。建立了牵引供电系统数学模型，将机车负荷作为恒功率模型，根据机车负荷和供电电压，分别采用牛顿-拉夫逊法和前推回代法，进行了直供和AT牵引供电系统潮流计算，通过典型算例比较了其与传统简化方法（机车负荷为恒电流模型）在机车网压计算的差异。结果表明，传统算法误差较大，尤其是在高速重载工况下误差更大，而电力系统潮流迭代方法进行牵引计算的精度更高。

牵引供电系统；潮流计算；电压损失；恒功率；迭代算法

随着电气化铁道高速客运和重载货运铁路的快速发展，牵引供电系统容量大幅增长，对供电能力和供电可靠性的要求更高。为了保证列车正常运行，牵引变电所两边供电分区的任何地点，牵引网电压都不得低于规定标准，所以在牵引供电系统中必须进行牵引网电压的计算。在牵引计算中，通常考虑发生在牵引网末端的最大电压损失，与机车取流位置有关。文献[1-2]给出了牵引计算的传统简化方法，由系统侧电压减去牵引变压器与牵引网的电压损失，得到牵引机车取流处电压；文献[3]利用连续线性潮流法，把已知的机车阻抗、负荷功率、戴维南等效模型用电流注入模型来表示，根据节点分析法求解出潮流方程。上述方法均将牵引机车作为恒电流负荷，将相量计算近似为标量计算，简化为线性问题，导致计算的不精确。并且机车从牵引网获取的电流受牵引网电压波动的影响较大[4-6]，会进一步增大传统算法的误差。

研究发现列车从牵引网获取的功率与牵引网电压波动无关，从这个角度来看，机车可以认为是恒功率负荷[7-11]。本文在此基础上，采用电力系统潮流计算迭代方法，针对直供系统和AT供电系统，分别建立其牵引变压器与牵引网的等值电路模型，考虑单个供电臂上不同数量机车负荷时机车取流处电压与牵引网的电压损失；进一步考虑当模型包含牵引变压器时，机车取流处电压与牵引网以及牵引变压器的电压损失。所采用的迭代方法将牵引供电系统潮流计算还原为非线性问题，相比传统算法的计算结果精度提高，并通过定义相对误差来定量分析使用迭代算法提高的精度，有效地避免了在设计时由于传统简化算法的误差而导致实际运行时机车处供电电压不足的问题，保证了电能质量与供电可靠性，对供电容量的设计具有重要的工程应用价值。

1 牵引供电系统潮流计算数学模型

牵引供电系统包含牵引变电所、牵引网与牵引机车。牵引变电所的核心元件是牵引变压器，目前多采用110 kV油浸式变压器，接线采用标准联结组，即YNd11，次边输出27.5 kV，比牵引网标准电压25 kV高10%[2]。供电方式多为直供或AT供电方式。典型牵引供电系统如图1所示。

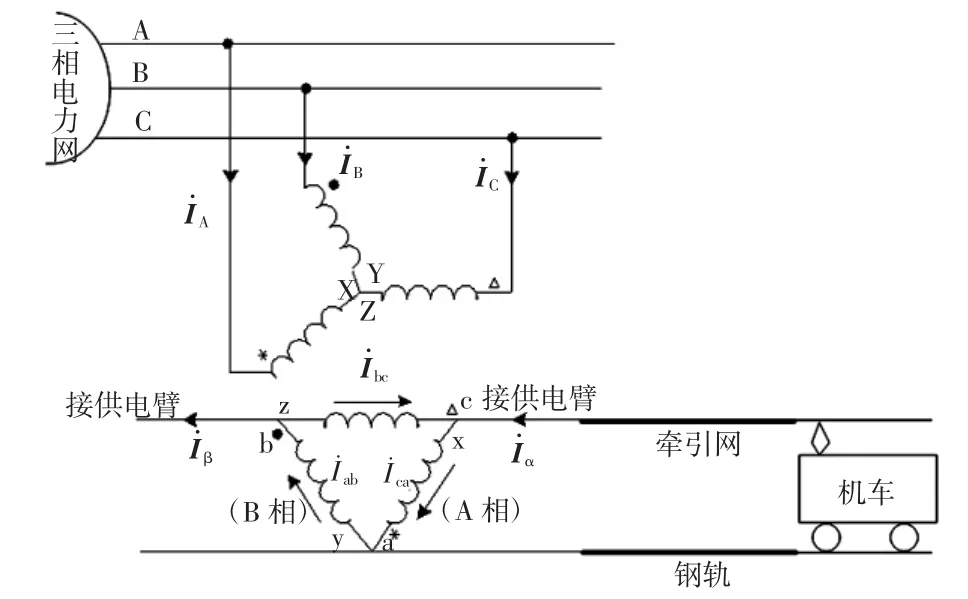
图1 牵引供电系统构成Fig.1 Structure of traction power supply system

1.1 三相YNd11牵引变压器数学模型

牵引变压器的三相等效模型如图2所示。

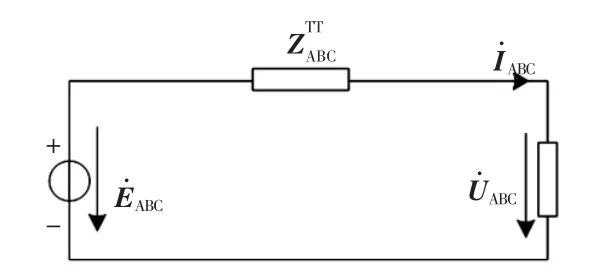
图2 牵引供电系统三相等效模型Fig.2 Three-phase equivalentmodelof traction power supply system

根据牵引变压器三相等效模型可知原边三相系统方程为

令γ相为自由相，即无负荷（I˙γ=0），由牵引变电所端口电气量通用变换关系[12]，可推导出牵引变压器α、β绕组感应电势为

式中：Kα、Kβ分别为次边端口电压模值与原边A相正序电压分量U˙+模值的变比；ψα、ψβ分别为次边端口电压滞后参考相量U˙+的相角，该值与变压器的接线形式和接入相序有关。对YNd11接线的牵引变压器，取Kα=Kβ=K==（k为变压器原边与次边相电压之比），ψα=0°，ψβ=ψα+ 120°，则电流电压变换矩阵变为

根据以上变换，可推导出系统等效到次边的阻抗阵。在式（1）两边左乘电压变换阵N得

根据式（6），且已知牵引变压器归算至原边的每相漏抗k2ZT，得变压器绕组漏抗归算至次边的漏抗阵为

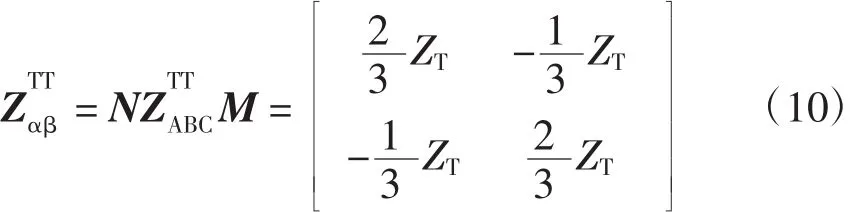
根据式（8），将变压器等效到次边，端口电压为

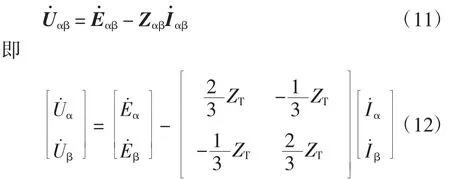
在本文算例中，仅考虑单个供电臂，只有机车负荷I˙α时，令I˙β=0，得端口电压为

1.2 直供方式牵引网数学模型

在单线直供方式下，牵引网以钢轨和大地作为牵引电流的返回导线。由于钢轨和大地之间存在过渡导纳，使得钢轨电流在流向牵引变电所的过程中，一部分形成地中电流（经过渡导纳逐渐泄入大地），一部分经过渡导纳进入钢轨（靠近牵引变电所的地区）。由于接触网-地回路与钢轨-地回路之间存在互阻抗，以及钢轨与地的接触，使得牵引电流在进入钢轨时，被分成感应电流和传导电流。为了简化分析和计算，在满足精度的前提下，认为钢轨-地回路只有感应电流。此时，单线直供牵引网可看作由2个导线网-地回路构成：接触网-地回路（有源网络）与钢轨-地回路（无源网络）。牵引网阻抗就是这2个导线-地回路网的综合阻抗，图3为单线直供牵引网简化电路模型。

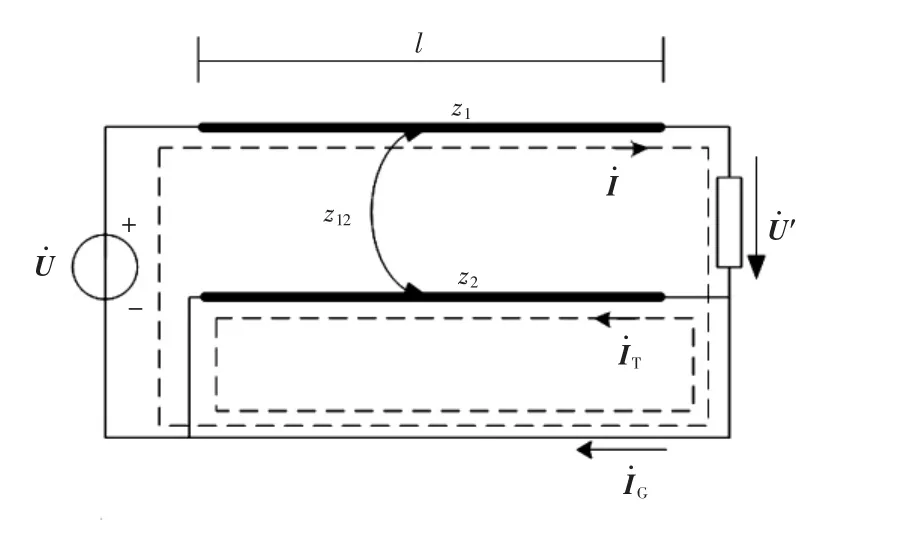
图3 单线直供牵引网简化电路模型Fig.3 Circuit modeloftraction network in the directsystem

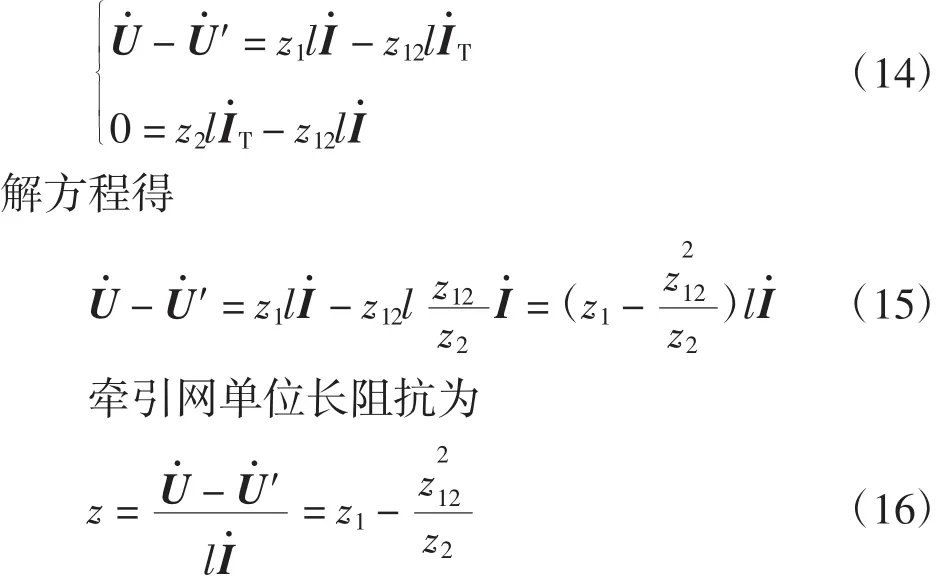
单线直供牵引网简化电路如图4所示。

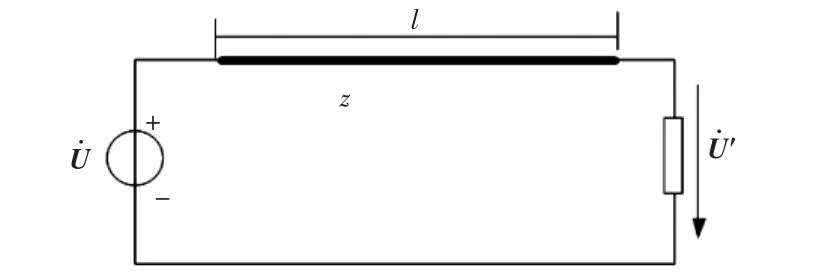
图4 单线直供牵引网等值电路模型Fig.4 Equivalentcircuit ofdirectsystem

1.3 AT供电方式牵引网数学模型

并联自耦变压器形成的AT供电方式，能显著降低电气化铁路对通信线路的干扰，牵引网阻抗小，供电距离长，牵引网上电压损失和电能损失都小，因此，AT供电方式是一种适用于高速、重载等大电流运行的牵引供电方式。电气化铁道供电电源由110 kV输电线将电送至牵引变电所，经牵引变压器将电压降低为55 kV（接触线与正馈线之间的电压），接触线与钢轨之间的电压为27.5 kV。牵引机车从27.5 kV接触线获得电能。若机车上的电压为′，则归算至牵引侧的牵引网压降为

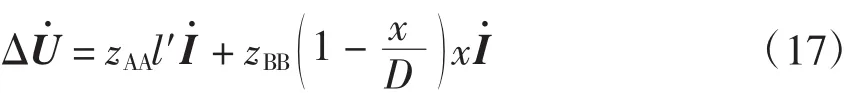
式中：l′为机车到牵引变电所的距离，km；x为机车到距离最近的自耦变压器（牵引变电所侧）的距离，km；D为相邻自耦变压器的距离，km；zAA与zBB的定义见文献[2]。

所以，归算到牵引侧的单线AT网络阻抗为

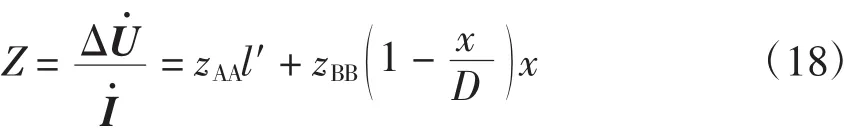
2 牵引供电系统潮流算法

2.1 传统算法

牵引供电系统潮流计算的传统算法只是进行简单的算术运算，其主要步骤如下。

步骤1假设α供电臂的负荷为I˙α，功率因数为cosφα；β供电臂断开，则三相YNd11牵引变压器电压损失为

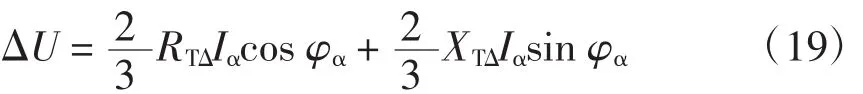
则变压器归算至低压侧的相阻抗为ZT=RTΔ+j XTΔ。

步骤2直接供电系统牵引网电压损失为

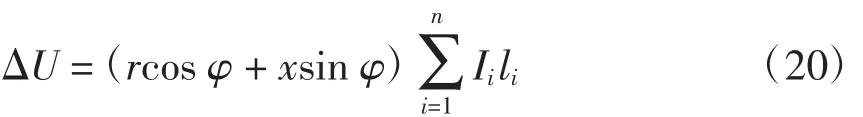
式中：Ii为机车取流处电流；φ为各机车功率因数角（由于各机车负荷功率因数变化不大，可认为均相等）；li为各机车到牵引变电所的距离。牵引网单位长阻抗为z=r+j x，Ω/km。

步骤3 AT供电系统牵引网电压损失如下：

（1）只有一列机车负荷时，牵引网电压损失计算见式（17）；

（2）当每个AT段一个机车负荷，且每个AT段中最多只有一个机车负荷存在时，牵引网电压损失的计算公式为

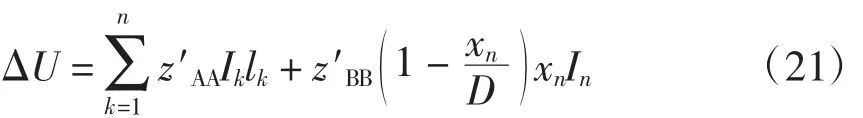
式中：Ik为第k个列车电流，A；lk为第k个列车至变电所距离，km；与的定义见文献[2]；视取流机车为电流源。

上述机车网压的传统计算方法中不存在迭代过程，前提条件是牵引网始端电压与末端电压的夹角很小。然而在高速重载铁路中，牵引网电流很大，牵引网始末端电压相角差已经有了较大的偏差，所以采用传统算法计算机车网压会产生较大的误差。因此，为了提高计算精度，引入迭代算法来计算列车网压。

2.2 迭代方法

本文采用电力系统中最基本的牛顿拉夫逊算法和前推回代算法来计算牵引供电系统潮流，并分析比较其与传统算法计算结果之间的相对误差。牛顿-拉夫逊（Newton-Raphson）算法使用函数f（x）的泰勒级数的前几项来寻找f（x）=0的根，最大的优点是在方程单根附近具有平方收敛性。牛顿-拉夫逊算法用于潮流计算具有计算精度高、收敛性好的特点，是电力系统潮流计算的经典算法[14]；前推回代算法的步骤简单，适用于辐射型网络[14]。两种算法都适用于本算例。

在利用牛顿-拉夫逊法求解牵引机车取流处电压时，假设牵引供电系统有n个节点，机车视为恒功率负荷，即机车取流处为PQ节点，计算时的潮流方程为

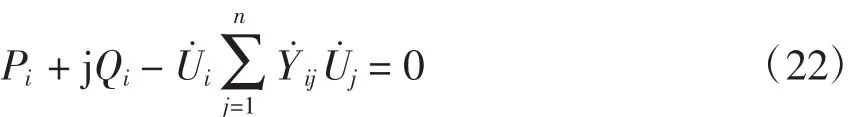
式中：Pi+j Qi为节点i的注入功率；为节点i的电压；U˙j为节点j的电压节点导纳矩阵元素。

当节点电压以直角坐标形式表示时，ei为节点电压实部，fi为节点电压虚部，功率方程可改写为

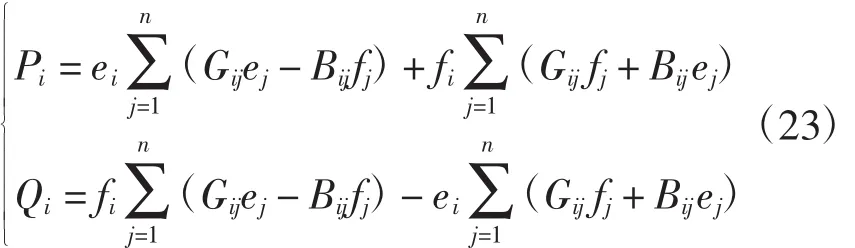
本文系统中，有1个平衡节点，则其余n-1个PQ节点的修正方程为

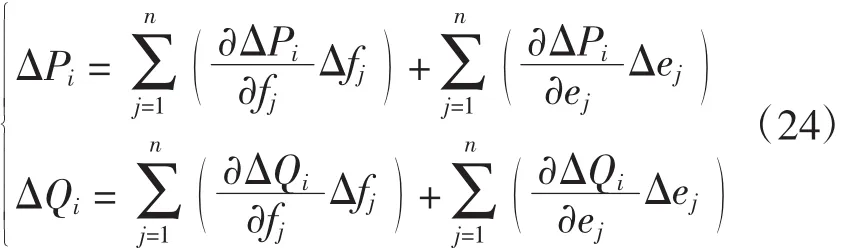
根据式（24）可求得本次迭代的修正量Δe和Δf，进而对电压进行修正，经反复计算，直到收敛到要求的精度。牛顿-拉夫逊算法计算潮流的具体流程如图5所示。

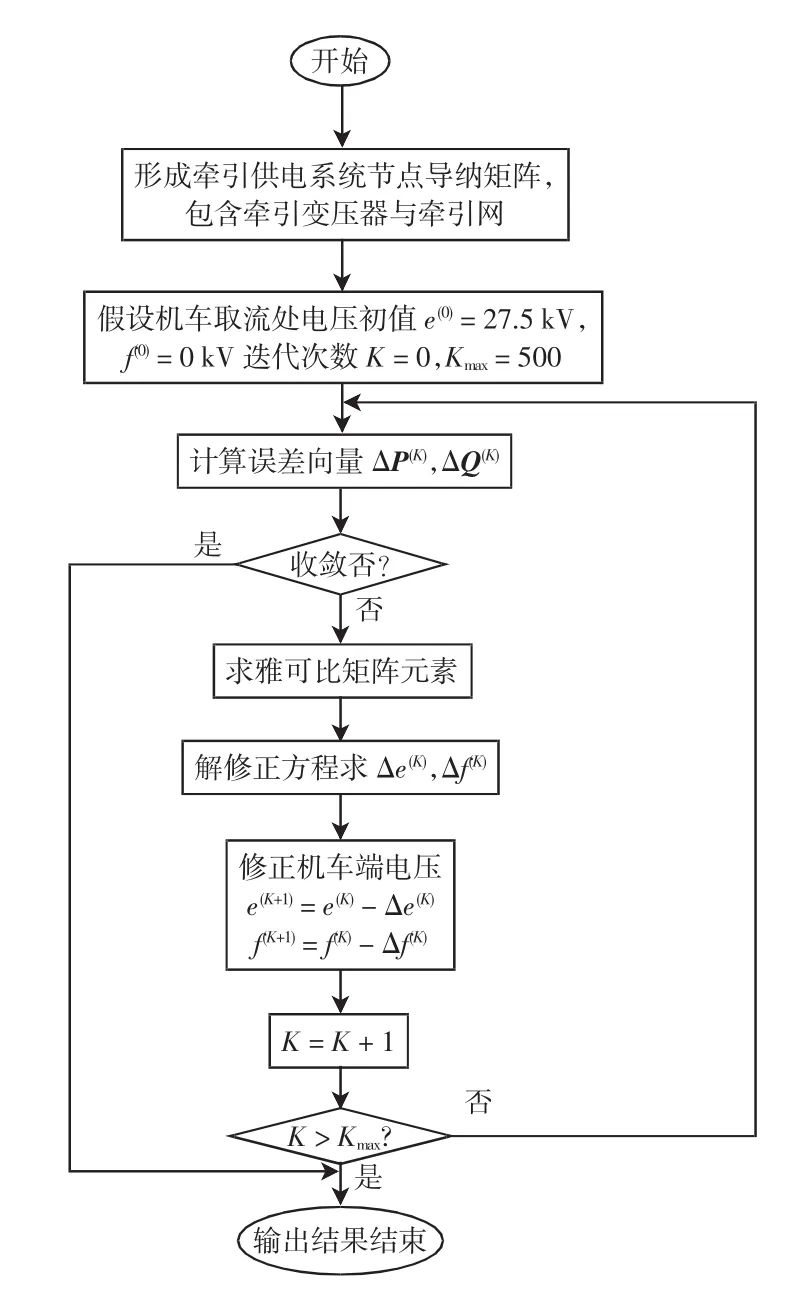
图5 牛顿-拉夫逊算法流程Fig.5 Flow chartof Newton-Raphson method

2.3 算例工况

算例分别考虑直供方式和AT供电方式，且每种供电方式中考虑以下3种情况：①只有牵引网；②包含牵引变压器；③机车数量不同。

根据列车的负荷功率和已知的始端电压，计算牵引供电系统列车网压。分以下2种情况：①只有牵引网时，已知馈线始端电压，假设为额定电压27.5 kV；②包含牵引变压器时，已知变压器高压侧电压，假设为额定电压27.5 kV。通过算例比较高速重载工况下传统算法和迭代算法的计算精度。

3 不同算法牵引供电系统潮流计算结果比较

已知某牵引供电系统的单个供电臂带有两列机车，负荷功率均为8.997+j4.357 MVA，线路始端电压为额定电压27.5 kV，Z12为变压器归算至低压侧的阻抗，Z12=0.061+j1.6805Ω，Z23为变电所出线处到#1机车取流处的牵引网阻抗，Z23=1.72+ j4.128Ω，Z34为#1机车到#2机车取流处之间的牵引网阻抗，Z34=1.505+j3.612Ω。牵引供电系统示意如图6所示。

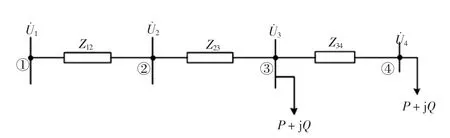
图6 牵引供电系统示意Fig.6 Sketch map oftraction power supply system

图中：节点①为变压器高压侧，是平衡节点，U˙1= 27.5 kV；节点②为变压器低压侧，即变电所出线处，是PQ节点；节点③为#1机车取流处，是PQ节点；节点④为#2机车取流处，是PQ节点。

1）传统算法

传统算法需要已知机车电流与始端电压。然而从机车功率求得机车电流的唯一方法是假设机车电压为额定电压27.5 kV，得到两列机车的电流均为˙it==0.327 2-j0.158 4 kA。计算得到变压器电压损失为0.572 3 kV，牵引网电压损失为3.497 9 kV，所以机车取流处电压为23.428 7 kV。

2）迭代算法

采用牛顿-拉夫逊算法进行牵引供电系统潮流计算，取精度为10-4。当迭代到第6次时，误差满足要求，此时的计算结果可作为最终计算结果。经KCL、KVL定律验证了潮流结果的正确性。迭代过程如表1所示。

表1 牛顿-算法迭代过程Tab.1 Iteration of Newton-Raphson algorithm kV

牛顿-拉夫逊法是求解非线性代数方程有效的迭代计算方法，在数学模型相同的基础上，其计算精度高于传统算法，计算结果更能反映实际电压值大小。本文认为，若忽略建模时产生的误差，则牛顿-拉夫逊法的计算结果可近似等效为实际电压值。

定义：相对误差=|传统算法列车端电压-牛顿-拉夫逊法列车端电压|/牛顿-拉夫逊法列车端电压×100%，用于比较二者在计算精确度上的差异。本算例中相对误差为5.968%，前推回代算法与牛顿-拉夫逊算法计算结果相同。

3.1 直接供电系统潮流计算

在直供系统中，已知牵引网单位长阻抗为z= 0.215+j0.516Ω/km，机车负荷功率均为P+j Q= 8.997+j4.357 MVA，YNd11牵引变压器容量为31.5 MVA，短路电压百分数为10.5%，变压器阻抗归算到负荷侧为zt=0.091 5+j2.520 8Ω，考虑单个供电臂，计算所得末端机车端电压大小如表2所示。

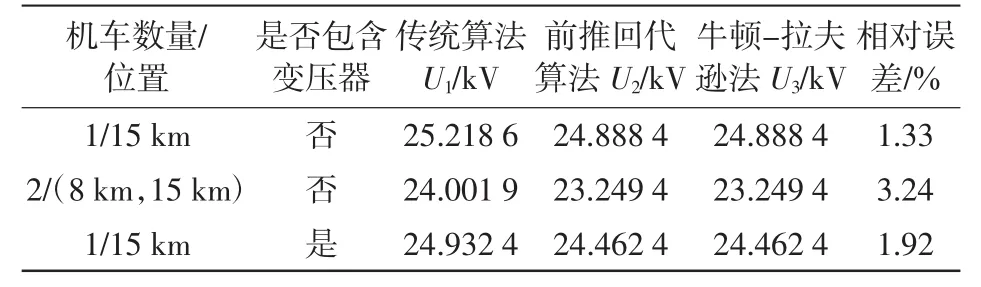
表2 直供方式下计算结果Tab.2 Results in directpower supply system

由表2的计算结果可知当机车数量越多，传统算法的相对误差越大；当包含牵引变压器时，传统算法的相对误差比不包含变压器时更大。

3.2 AT供电系统潮流计算

在AT供电系统中，牵引网参数[13]如表3所示。

在本算例中，已知机车负荷功率均为P+j Q= 8.997+j4.357 MVA，YNd11牵引变压器容量为31.5 MVA，短路电压百分数为10.5%，变压器阻抗归算到负荷侧为zt=0.091 5+j2.520 8Ω，考虑单个供电臂。计算所得末端机车端电压大小如表4所示。

由表4的计算结果，可知机车数量越多，传统算法的相对误差越大；当包含变压器时，传统算法的相对误差比不包含变压器时更大。

表3 AT供电牵引网参数Tab.3 Parameters oftraction network in AT mode Ω/km

表4 AT供电方式下计算结果Tab.4 Results in the AT-fed power supply system

4 结论

为了提高牵引供电系统潮流计算的精度，本文将机车负荷作为恒功率模型，采用电力系统中潮流计算的迭代方法进行牵引供电系统潮流计算，通过不同工况算例比较了传统算法与迭代算法的精度，主要结论如下。

（1）当牵引网机车负荷越重，例如机车数量越多时，传统算法计算的机车处电压的误差越大。在AT供电系统中，当只有1列机车时，传统算法的相对误差为1.55%；当有4列机车时，传统算法的相对误差为9.88%。

（2）包含牵引变压器时，传统算法计算的误差会变大。在AT供电系统中有4列机车，不包含变压器时，传统算法的相对误差为9.88%；当包含变压器时，传统算法的相对误差为14.94%。

（3）在高速重载工况下，机车负荷更大，用传统简化算法的误差也较大，会导致对供电能力计算的较大误差。根据我国电气化铁道设计、运行经验，接触网标称电压为25 kV，长期最高电压为27.5 kV，设计最低电压为20 kV。在算例AT供电系统中，带有4列机车且包含牵引变压器时，用牛顿-拉夫逊法计算的机车电压为19.305 4 kV，而简化方法计算得到的结果为22.189 3 kV。显然，依据传统简化算法得到的数据进行的设计可能导致实际运行中的供电能力不足，即实际运行时机车处供电电压不足。

[1]曹建猷.电气化铁道供电系统[M].北京：中国铁道出版社，1983.

[2]李群湛，贺建闽.牵引供电系统分析[M].成都：西南交通大学出版社，2007.

[3]Goodman C J，Kulworawanichpong T.Sequential linear power flow solution for AC electric railway power supply system[C]//Computers in Railways Eighth International Conference.Lemnos，Greece：2002.

[4]唐开林，李群湛，张丽艳，等（Tang Kailin，Li Qunzhan，Zhang Liyan，etal）.电气化铁道牵引网馈线电流概率分布（Probability distribution offeeder currentofelectrified railway traction）[J].电力系统及其自动化学报（Proceedings ofthe CSU-EPSA），2010，22（6）：12-16.

[5]张永旺，李欣然，李金鑫，等（Zhang Yongwang，LiXinran，Li Jinxin，et al）.牵引供电系统综合负荷实测建模（Measurement-based composite load modeling of traction power supply system）[J].电力系统及其自动化学报（Proceedings ofthe CSU-EPSA），2012，24（1）：94-99.

[6]胡宗耀，李欣然，朱湘有，等（Hu Zongyao，Li Xinran，Zhu Xiangyou，etal）.电气化铁路牵引负荷的支持向量机负序源建模（Modelofsupportvector machine negative sequence characteristics ofelectrified railway traction loads）[J].电力系统及其自动化学报（Proceedings ofthe CSUEPSA），2010，22（3）：102-107.

[7]万庆祝，吴命利，陈建业，等（Wan Qingzhu，Wu Mingli，Chen Jianye，etal）.基于牵引计算的牵引变电所馈线电流仿真计算（Simulating calculation oftraction substation’s feeder currentbased on traction calculation）[J].电工技术学报（Transactions of China Electrotechnical Society），2007，22（6）：108-113.

[8]何俊文，李群湛，刘炜，等（He Junwen，Li Qunzhan，Liu Wei，etal）.交流牵引供电系统仿真通用数学模型及其应用（General mathematical model for simulation of AC traction power supply system and its application）[J].电网技术（Power System Technology），2010，34（7）：25-29.

[9]何正友，方雷，郭东，等（He Zhengyou，Fang Lei，Guo Dong，etal）.基于AT等值电路的牵引网潮流计算方法（Algorithm for power flow of electric traction network based on equivalent circuit of AT-ed system）[J].西南交通大学学报（Journal of Southwest Jiaotong University），2008，43（1）：1-7.

[10]陈宏伟，耿光超，江全元（Chen Hongwei，Geng Guangchao，Jiang Quanyuan）.电气化铁路牵引供电系统车网耦合的潮流计算方法（Power flow algorithm for traction power supply system of electric railway based on locomotive and network coupling）[J].电力系统自动化（Automation of Electric Power Systems），2012，36（3）：76-80，110.

[11]池云莉，何天健，梁嘉杰（Chi Yunli，He Tianjian，Liang Jiajie）.电气化铁道系统概率潮流算法研究（Probabilistic load flow study for electric railway）[J].电气化铁道（Electric Railway），2004，（6）：4-8.

[12]李群湛（LiQunzhan）.牵引变电所电气量的通用变换方法及其应用（A generalized transforming method for electrical values in AC traction substations and its applications）[J].铁道学报（Journalofthe China Railway Society），1994，16（1）：17-23.

[13]郭东，杨健维，何正友，等（Guo Dong，Yang Jianxiong，He Zhengyou，etal）.一种基于牛顿法的交流高速铁路牵引供电潮流计算方法的研究（Research on a flow analysis method of power supply system for AC high speed railway based on Newton method）[J].继电器（Relay），2007，35（18）：16-20，29.

[14]韩祯祥．电力系统分析[M]．杭州：浙江大学出版社，2005．

A Power Flow Analysis Method of Traction Power Supply System Based on Constant-power Load

WANG Fang，WANG Xiaoru
（SchoolofElectric Engineering，SouthwestJiaotong University，Chengdu 610031，China）

This paper introduces a method to the traction power supply system based on power flow iterative algorithm of the power system.Mathematical models of the traction power supply system are established.The locomotive load is regarded as a constant-power modelinstead of a constant-current one.The Newton-Raphson method and forward and backward substitution method are used to calculate the voltage of locomotive and voltage loss of traction network and traction transformer respectively，and both directpower supply system and AT fed system are taken into consideration. The results are compared with those calculated by the traditional simplified method for the same typical examples.It shows thatthere are large deviations in the results ofpower flow calculation for traction power supply system using the traditionalsimplified method，especially in high-speed orheavy-load conditions，while the accuracy ofresults by powerflow iterative algorithm is much higher.

traction powersystem；powerflow calculation；voltage loss；constant-power；iterative algorithm

王芳（1988—），女，硕士研究生，研究方向为牵引供电系统供电能力。Email：wangfang2014@126.com

2013-05-09；

2013-07-18

TM744；TM922.3

A

1003-8930（2015）03-0059-06

10.3969/j.issn.1003-8930.2015.03.11

王晓茹（1962—），女，博士，教授，博士生导师，研究方向为电力系统保护和安全稳定控制、变电站自动化、牵引供电系统与电力系统之间相互影响等。Email：xrwang@home.swjtu. edu.cn