双凯塞窗在旁瓣抑制技术中的应用

董绍雄，王 平

(西华大学电气信息学院，四川 成都 610039)

· 机电工程·

双凯塞窗在旁瓣抑制技术中的应用

董绍雄，王 平*

(西华大学电气信息学院，四川 成都 610039)

在分析线性调频和巴克码组合调制信号的脉冲压缩原理基础上，对比研究加权海明窗或汉宁窗进行旁瓣抑制的常规方法，提出一种在发射机和接收机中同时加Kaiser窗加权的方法。与加海明窗主旁瓣比达到-42 dB和加汉宁窗主旁瓣比达到-31.4 dB相比较，双Kaiser窗法可以使脉冲压缩后的主旁瓣比达到-50 dB以下，具有更好的旁瓣特性，同时脉冲压缩后主瓣展宽幅度也相对较小。

脉冲压缩技术；旁瓣抑制；双凯塞窗;线性调频和巴克码组合调制信号;匹配滤波

脉冲压缩信号通过匹配滤波后，在主瓣的两侧会出现幅度低于主瓣的一系列距离旁瓣。距离旁瓣的存在是有害的，因为大目标的旁瓣较高，会被误认为是目标主瓣，出现目标判定错误。另外，大目标的旁瓣还会压制临近的较小目标的主瓣，导致小目标检测不到。为此，应在进行脉冲压缩处理的同时，引入旁瓣抑制技术。

从上世纪50年代以来，旁瓣抑制的研究取得了很多成果[1-4]。对于LFM信号，目前最常用的是直接加权加窗函数(如巴特利特窗、汉宁窗、海明窗、三角窗等)方法，其本质就是对信号进行失配处理，在脉冲压缩滤波器后面级联一个频率响应具有某种锥削函数的副瓣抑制滤波器。直接加权加窗函数法虽然能降低旁瓣、提高主旁瓣比，但是将带来信噪比损失和主瓣展宽的问题。本文研究的是现代雷达采用的线性调频和巴克码组合调制信号[5-7]，该信号的脉冲压缩处理的实质是设计匹配滤波器。通常情况下，经过匹配滤波处理，信号的主旁瓣比很低，在多目标情况下，会出现目标误判和小目标的丢失，不能达到性能要求。本文在对线性调频和巴克码组合调制信号的脉冲压缩原理进行分析的基础上， 对比研究了其旁瓣抑制的2种常规方法,提出一种采用双凯塞窗加权来抑制旁瓣的方法。

1 线性调频和巴克码组合调制信号的脉冲压缩原理

脉冲压缩可以通过时域卷积法或者频域快速傅里叶变换法来实现。 脉冲压缩滤波器的延迟频率特性与发射信号变化规律相反，即脉冲压缩器的相频特性与发射信号的相位是共轭匹配。这就是匹配滤波器实现脉冲压缩的原理[8]。具体实现过程是通过对接收信号x(n)和匹配滤波响应h(n)求卷积得出。设输入信号为x(n)，其时域脉冲压缩[8]可以表示为

(1)

时域卷积对应的是频域相乘，所以可以在频域实现脉冲压缩。频域快速傅里叶变换法[9]是先对输入信号进行快速傅里叶变换，接着与脉冲压缩系数相乘，然后进行逆变换，得到脉冲压缩结果，如图1所示。变换之前补零是为了使输入信号序列长度和滤波器的长度相同。

图1 频域脉冲压缩

线性调频和巴克码组合调制信号的脉冲压缩处理可以分成2步：首先经过线性调频的匹配滤波器，得到相位编码脉冲信号，然后通过相位编码的匹配滤波器，得到最终的脉冲压缩信号。2步脉冲压缩过程也可1步完成[5]。

线性调频和巴克码组合调制信号通过匹配滤波器输出后，信号幅度曲线近似为辛格函数。经过试验得出，脉压输出信号的最大旁瓣约为主瓣电平的-13.2 dB，其他旁瓣随其离主瓣的间隔x按1/X的规律衰减，旁瓣零点间隔为1/B。主瓣顶点下-4 dB处的宽度约为1/B，即主瓣宽度是一个重要参数，它决定了雷达距离分辨力的大小。主瓣的宽度越小距离分辨力越大。

2 目前2种常规旁瓣抑制方法的优劣性分析

实际上，不管是时域卷积法还是频域快速傅里叶变换法，旁瓣问题总是存在的。实际雷达中必须对旁瓣进行抑制。旁瓣可以通过加权技术来抑制，加权可以单独在发射端或接收端进行也可在收发两端同时加权。无论是时域还是频域都可以对幅度或者相位进行加权。目前常用的方法是在频域或时域内对匹配滤波器的权值加窗函数进行加权。一般情况下，选择一个适当的加权函数，乘以匹配滤波器函数，再进行匹配滤波处理，从而达到降低旁瓣的目的。常用的加权函数有巴特利特窗、汉宁窗、海明窗和三角窗[5]。加窗后的脉冲压缩系数可以表示为

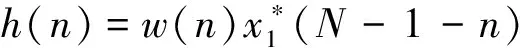
(2)

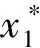
2.1 海明窗加权的脉冲压缩算法

海明窗函数[10]的形式为

(3)

其频域响应为WHm(ejω)=0.54WR(ω)+

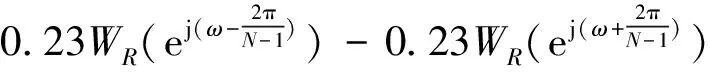
假设输入的线性调频和巴克码组合调制信号中频f0=30 MHz，带宽B=4 MHz，时宽T=10μs，巴克码位数P=13，采样频率fs=100 MHz，对该信号进行脉冲压缩，并利用海明窗函数加权对其进行旁瓣抑制，其仿真结果如图2所示。

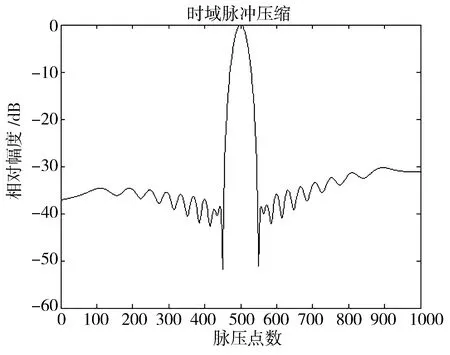
图2 加海明窗的旁瓣抑制效果

可以看出：加窗后主旁瓣比达到-42 dB，与未加窗函数相比，主旁瓣比得到很大提高；主瓣宽度得到增加，从而使距离分辨力降低了。加窗以后整个脉冲压缩过程就不再是匹配滤波，这必将导致信噪比SNR降低，雷达检测微弱目标的能力也将降低。

2.2 汉宁窗加权的脉冲压缩算法

汉宁窗函数[10]的形式为

(4)

其频域响应为WHn(ejω)=[0.5WR(ω)+

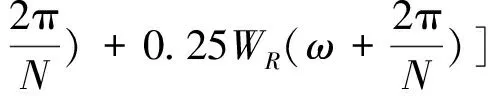
假设输入的线性调频和巴克码组合调制信号中频f0=30 MHz，带宽B=4 MHz，时宽T=10μs，巴克码位数P=13，采样频率fs=100 MHz，对该信号进行脉冲压缩，并利用汉宁窗函数加权对其进行旁瓣抑制，其仿真结果如图3所示。

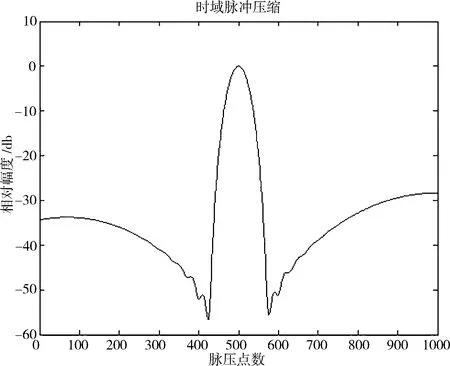
图3 加汉宁窗的旁瓣抑制效果

可以看出：脉冲压缩以后主旁瓣比为-31.4 dB，比加海明窗低；主瓣宽度比加海明窗后的还要大，其性能较海明窗函数差。

3 双Kaiser窗加权的脉冲压缩算法

通过对上面的2种窗函数法的应用结果分析可知，对匹配滤波器函数进行海明窗函数和汉宁窗函数的加权，虽然在一定程度主旁瓣比会得到提高，但会导致主瓣展宽，从而降低了距离分辨力、信噪比SNR和微弱信号的检测能力。为此，本文提出一种应用双凯塞窗进行加权降低旁瓣的方法，并对其进行了分析和比较。

根据谱修正技术，TB值越大，经过窗函数加权后的脉冲压缩波形的旁瓣越低，TB值越小，旁瓣越高。频域上的边缘跃变和菲涅尔波纹的存在是造成这个现象的原因[11]。TB值较大时，振幅谱接近矩形；TB值越大，菲尼尔纹波越小，主旁瓣比也越高。旁瓣抑制的方法都是使调频信号具有光滑的包络，平滑其边缘跃变，最终达到减小旁瓣的目的。双Kaiser窗算法是在发射机和接收机中同时应用Kaiser窗函数进行加权，发射信号经过加窗处理后不再具有原线性调频信号的频谱特点，边缘的阶跃性大大的减小，菲涅尔纹波也减小，从而有效降低了旁瓣。Kaiser窗函数是一种零阶长球面波函数，根据零阶第一类修正的贝塞尔(Bessel)函数近似得到在截取有限时宽信号时使频宽内的能量为最大,从而有效地抑制旁瓣的影响[12]，其函数为：

(5)

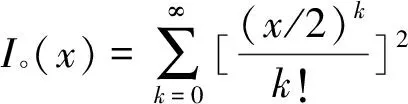
(6)

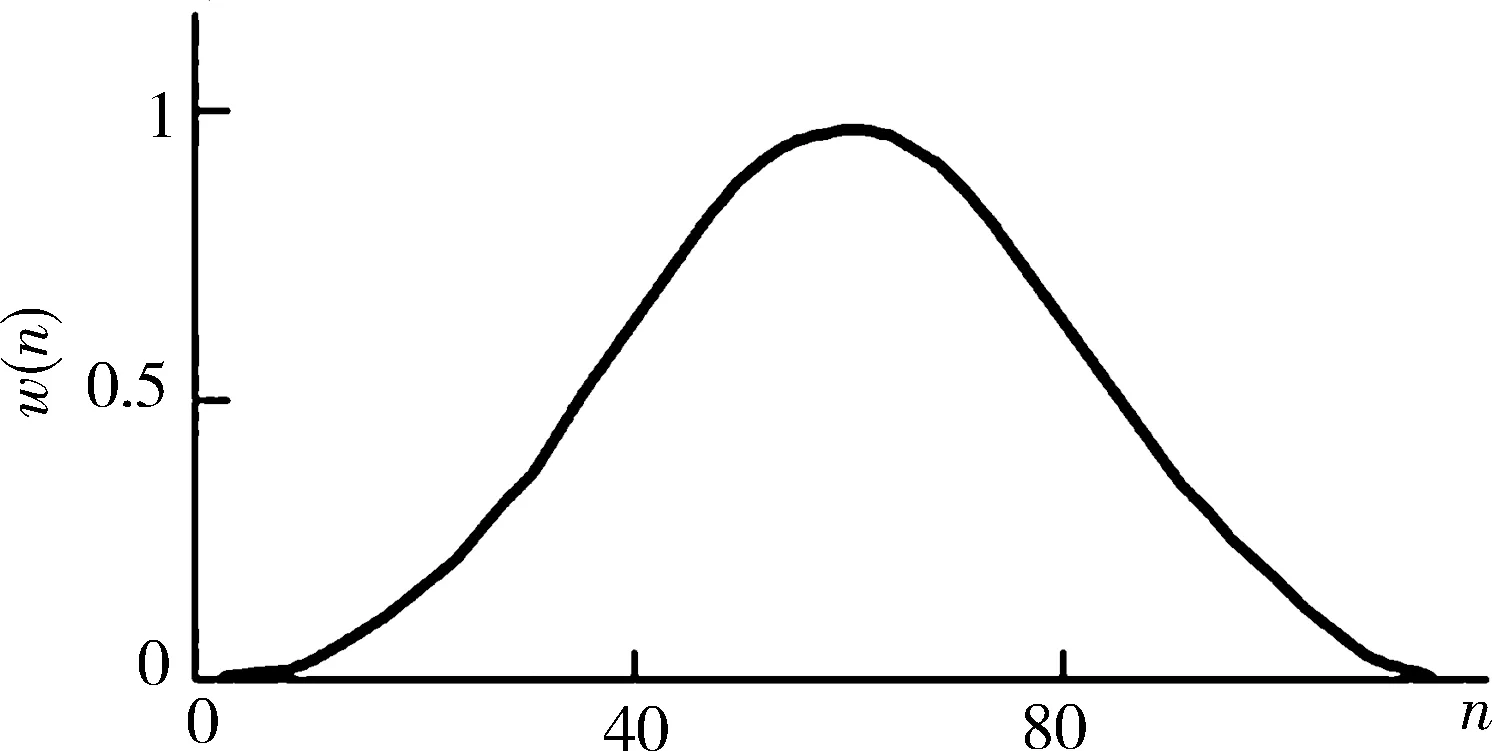
(a)Kaiser窗函数

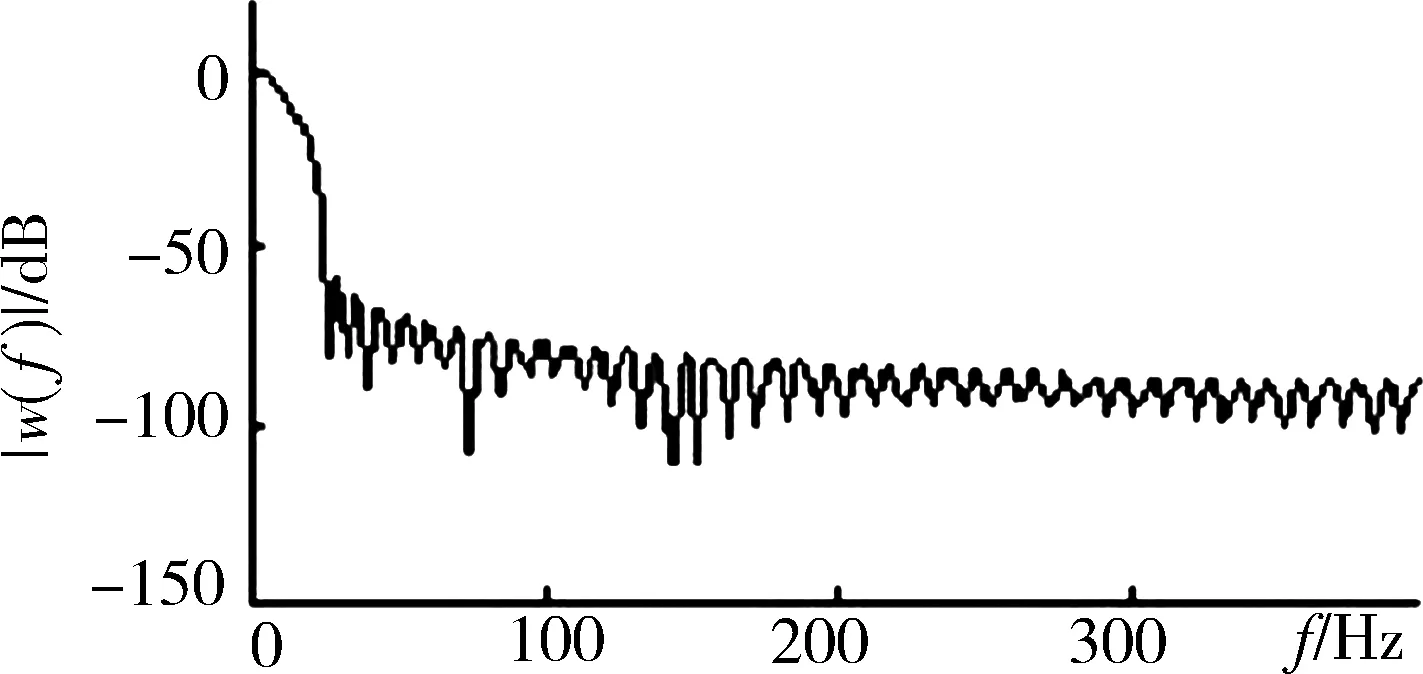
(b)Kaiser窗谱

设输入信号为x(n),双Kaiser窗加权的脉冲压缩算法流程图如图5所示。

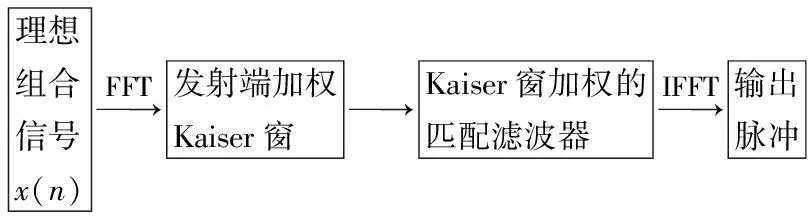
图5 双Kaiser窗加权的脉冲压缩算法流程图

在图6中，实线是加了Kaiser窗的发射信号，其中Kaiser的参数设置为8。可以看出，发射信号经过加窗处理后不再具有原线性调频信号的频谱特点，边缘的阶跃性大大地减小，从而有效降低了旁瓣。其脉冲压缩效果如图7所示。

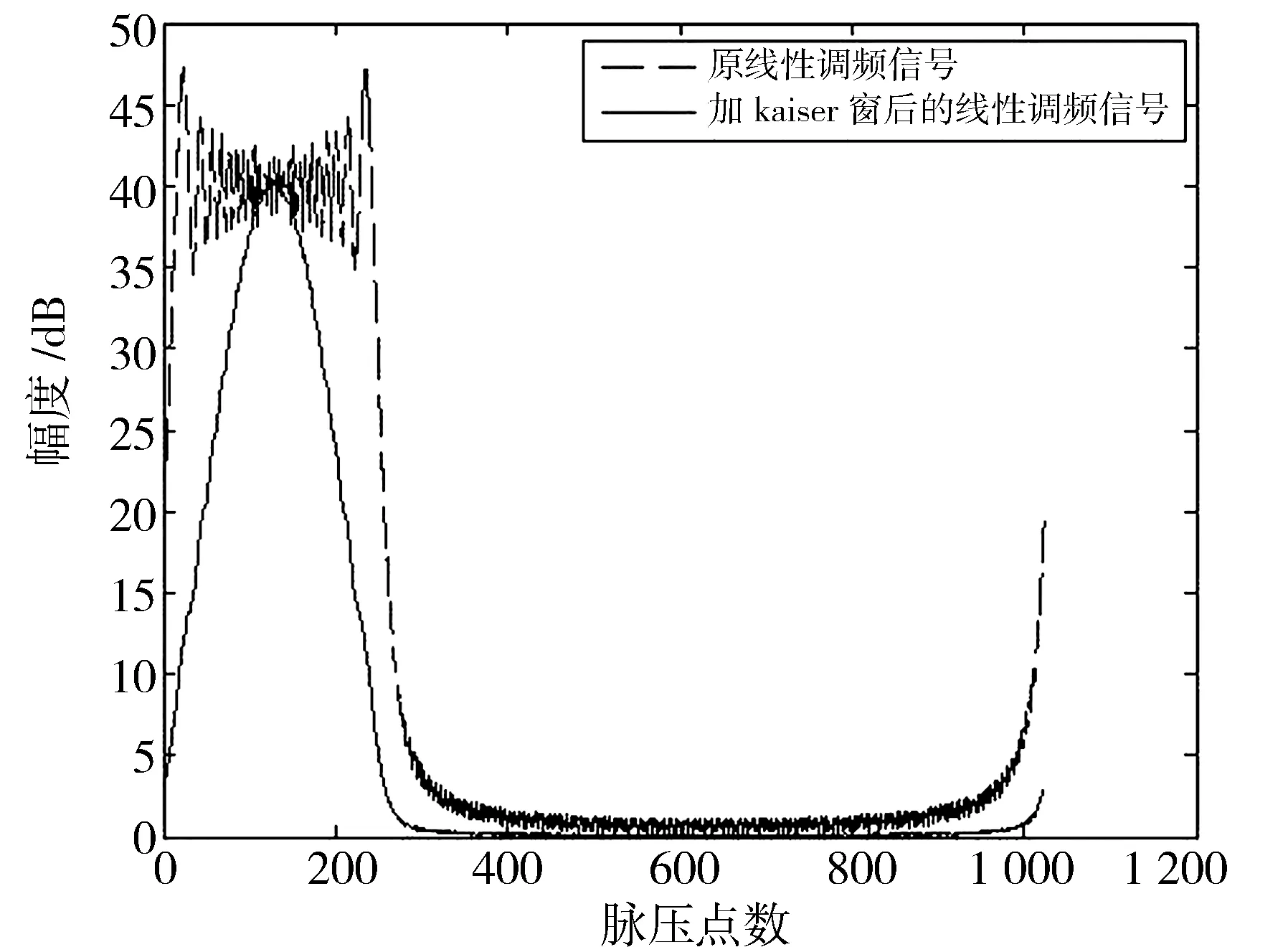
图6 2种信号的幅度谱

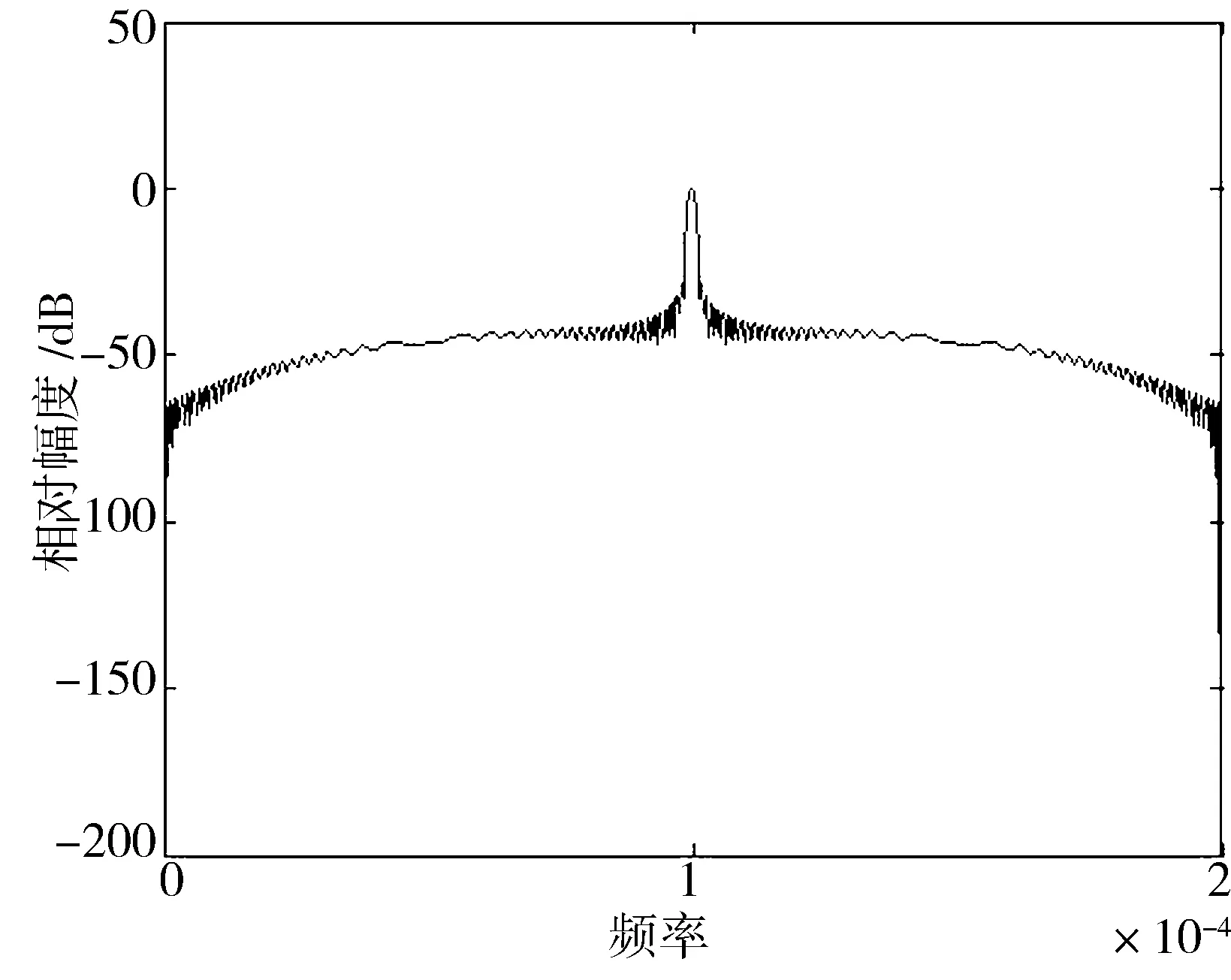
图7 加Kaiser窗的发射信号脉冲压缩结果

可以看出，当不加窗时，组合信号脉压后的主旁瓣比约-13.2 dB，加窗后，主旁瓣比大大提高，但主瓣展宽且幅度降低。加海明窗后主旁瓣比能提高到-42 dB左右，与加海明窗比，加汉宁窗后主旁瓣比会达到-31.4 dB，双Kaiser窗法可以使脉冲压缩后的主旁瓣比明显增加，主旁瓣比可以到达-50 dB以下，主瓣宽度的增加幅度相对上述2种方法也较小。双凯塞窗法的优点在于性能具有可调性，可以通过设置参数β来得到所需要的主旁瓣比。

实际应用中，发射信号要通过功率放大器进行功率放大，然而功率放大器的工作点在很多情况下都设在饱和区或接近饱和区；因此，加Kaiser窗以后的发射信号将会出现严重的幅度失真，即功率放大器的非线性失真。为解决此问题进行如下改进。设x(t)为线性调频和巴克码组合调制信号，w(t)是Kaiser窗函数，谱修正后的滤波器为h(t)，则图5中的双Kaiser窗加权的脉冲压缩算法可表示为

x(t)*h(t)=x(t)w(t)*[s(T-t)w*(T-t)]。

(7)

由式(7)可以求得谱修正后的滤波器的频率响应

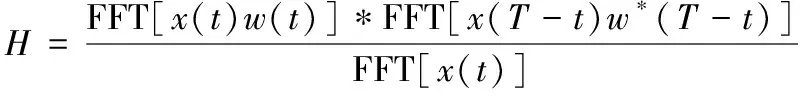
(8)

这样，在加权过程中，在发射端就不用进行Kaiser窗加权，发射信号仍为线性调频和巴克码组合调制信号，只在接收端等效加权，由式(8)得到的滤波器频率响应进行。而双Kaiser窗加权的脉冲压缩算法流程如图1所示，只不过此时加权的脉冲压缩系数替换为式(8)得到的H。

4 结束语

本文通过理论分析和仿真对比，探讨了双凯塞窗加权算法在旁瓣抑制中的应用以及优越性。对匹配滤波器函数进行海明窗函数和汉宁窗函数的加权，虽然在一定程度上主旁瓣比会得到提高，但这2种方法会导致主瓣展宽，从而降低距离分辨力和信噪比SNR。双凯塞窗加权算法是在发射机和接收机中同时用Kaiser窗加权，发射信号频谱得到了很好的平滑，具有Kaiser窗的形状，频谱边缘幅度缓慢下降，并且菲涅尔纹波也减小了，因此得到了很好的主旁瓣特性，主旁瓣比可以达到-50 dB以下,同时主瓣宽度的增加幅度相对上述2种方法也较小。双Kaiser窗加权算法是加窗旁瓣抑制技术的一种新方法。

[1]Rihaczek A W, Golden R M.Range Sidelobe Suppression for Barker Codes[J].IEEE Transactions on Aerospace and Electronic Systems,1971,7(6):1087-1092.

[2]张仕元，吴乐南. 基于RLS的脉压雷达数字旁瓣抑制滤波器设计方法[J].测控技术,2006,25(7):79-82.

[3]Ackroyd M H，Ghani F．Optimum Mismatched Filters for Side-lobe Suppression[J]．IEEE Trans on AES，1973，9(2):214-217．

[4]Zoraster S. Minimum Peak Range Sidelobe Filters for Binary Phase-coded Waveforms[J]．IEEE Transactions on Aerospace and Electronic Systems，1980 ,16(1):112-115．

[5]张静.脉冲压缩及其旁瓣抑制技术研究[D].西安：西安电子科技大学，2005.

[6]于超鹏, 郝亮飞, 谢金华.线性调频和巴克码组合调制雷达信号[J].探测与控制学报，2009,31(5):20-24.

[7]张静，赵平平，贾佳，等.基于相对判决准则的LFM信号Wigner-Hough变换检测方法研究[J].西华大学学报：自然科学版，2013，32(4)：67-70.

[8]张云龙. 雷达微弱目标检测算法研究[D].杭州：杭州电子科技大学，2012.

[9]张军.大时宽带宽积信号的脉冲压缩及优化实现结构 [D].西安：西安电子科技大学，2011.

[10]张德丰.MATLAB数字信号处理与应用[M].北京：清华大学出版社，2010：225-237.

[11]王宣芬，李巍，王子立.一种实现超低旁瓣的脉冲压缩算法[J].现代电子技术，2009(23)：5-7.

[12]何益宏，卓放，李红雨. Kaiser 窗在谐波电流检测中的应用[J].电网技术，2003,27(1):9-12.

(编校：饶莉)

DoubleKaiserWindowApplicationintheSidelobeSuppressionTechnology

DONG Shao-xiong,WANG Ping*

(SchoolofElectricalandInformationEngineering,XihuaUniversity,Chengdu610039China)

Based on the analysis of linear frequency modulation and Barker code combined modulation signal pulse compression, the ordinary methods of side-lobe suppression with weighted Hamming window or Hanning window were compared and researched. Finally, a novel method is proposed. For the method, weighted Kaiser window is utilized in both the transmitter and receiver. Compared with weighted Hamming window which ratio of main-lobe and side-lobe reaches -42 dB and weighted Hanning window which ratio of main-lobe and side-lobe reaches -31.4 dB, double Kaiser window method can let the compression ratio reach above -50 dB and shows its better side-lobe performance. After the pulse compression, its main-lobe broadening range is relatively small.

pulse compression; sidelobe suppression; dual Kaiser window;linear FM and barker code combined modulation signal;match filter

2014-01-21

教育部春晖计划项目(Z2012029)；四川省高等学校科技创新重大培育项目(09zz029)。

： 王平(1970—)，男，教授，博士，主要研究方向为嵌入式计算机系统、信息处理及信息融合、集成传感器系统等。E-mail：ping_wang@126.com

TN958.3

：A

：1673-159X(2015)01-0076-04

10.3969/j.issn.1673-159X.2015.01.013

*