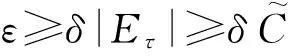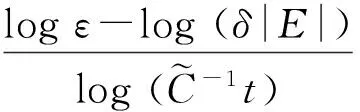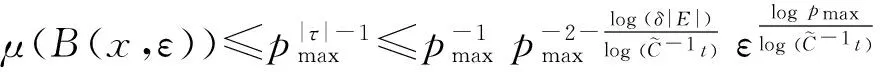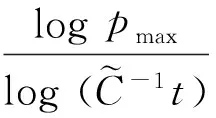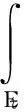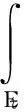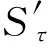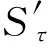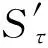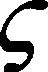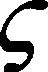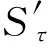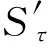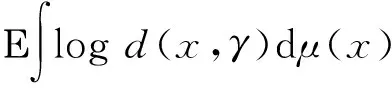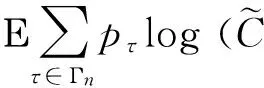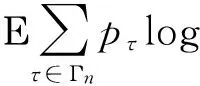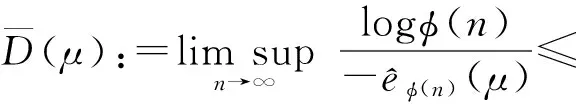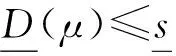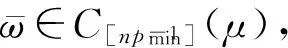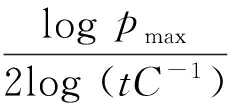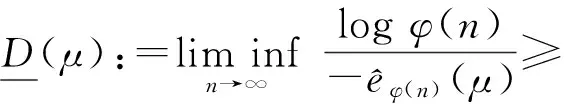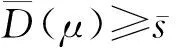随机自共形测度关于几何均值误差的量子化维数
2015-07-18王春敏
王春敏
(江苏联合职业技术学院镇江分院 基础部,江苏 镇江 212016)
随机自共形测度关于几何均值误差的量子化维数
王春敏
(江苏联合职业技术学院镇江分院 基础部,江苏 镇江 212016)
主要证明强分离条件下,随机自共形测度关于几何均值误差的量子化维数与其Hausdorff维数相等。
随机自共形测度;量子化维数;强分离条件
1 几何均值误差的量子化维数及主要结果
量子化问题起源于信号传输和数据压缩的相关理论。从数学角度来讲,量子化的主要意义在于用具有有限支撑的离散概率测度逼近给定的概率测度。用分形进行量子化处理的噪声趋向于0的速度明显快于欧式空间中的普通子集。量子化维数的定义最先由Zador[1]给出,随着人们对随机分形集所支撑的测度产生兴趣,许多研究者开始探索随机测度的多重分形性质与维数,Arbeiter与Patzschke[2]探讨了随机自相似测度的多重分形性质,给出了随机自相似测度的Hausdorff维数公式。在随机测度的量子化维数研究方面,Dai与Tan[3]探讨了随机自相似测度的量子化维数,并证明了随机自相似测度与其分布之间的关系。Zhu[4]研究了r→0时自共形测度的量子化维数的几何误差,即当r→0时,r阶量子化误差收敛于几何均值误差[1]。而与非随机分形相比,随机分形通常与自然现象更接近。研究随机测度μ关于几何均值误差的量子化维数及其与Hausdorff维数之间的关系非常有意义。
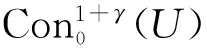
|S′(x)-S′(y)|≤CS|x-y|γ,
x,y∈U,其中S′(x)是S在x处的导数,|S′(x)|是导数的算子范数。
令N≥2且是整数,给出N个共形微分同胚Si:U→Si(U),i=1,…,N,考虑积空间
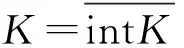
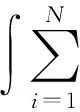
那么满足上述3个条件的(Ω0,F0)上的概率测度P0叫做随机共形函数系。
对随机变量(S1,…,SN;p1,…,pN),如果有
那么这个唯一的紧致随机集E⊂U称为与P0相关的随机自共形集,其中Ei(i=1,2,…,N)是E独立于(S1,…,SN;p1,…,pN)的复制。类似地,存在使得supp(Φ)=E的与P0相关的有限随机测度μ满足
其中μi(i=1,2,…,N)是μ独立于(S1,…,SN;p1,…,pN)的复制。若Si是相似映射,则上述随机集是自相似集,测度是随机自相似测度。
由文献[5]可知,Rd上随机测度μ关于几何均值误差的量子化误差定义为
(1)
其中
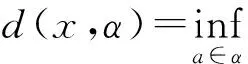
如果对某些 1≤card(α)≤n的集合α⊂Rd,式(1)中的最小值能够取到,那么这个集合α叫做μ的n-最优集。n-最优集的全体用Cn(μ)表示。在某些约束条件下,当n→∞时,en(μ)→0。定义
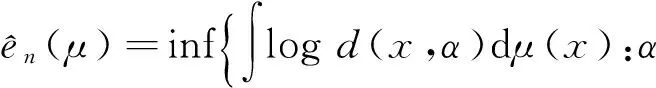
(2)
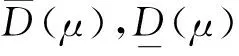
如果
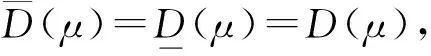
则D(μ)称为μ关于几何均值误差的量子化维数。
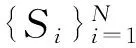
Graf与Luschgy[5]证明了开集条件下,Rd上自相似测度的0阶量子化维数等于其Hausdorff维数,Zhu[4]证明了强分离条件下自共形测度有相同的结论。本文主要证明强分离条件下,支撑在随机自共形集E上的随机自共形测度关于几何均值误差的量子化维数与其Hausdorff维数相等。
定理强分离条件下,与随机变量(S1,…,SN;p1,…,pN)相关的随机自共形测度μ有
D(μ)=dimH(μ)
以概率1成立。
2 随机自共形测度及相关性质
用[σ]={τ∈Σ:στ}表示以σ开头的序列的柱集,其中σ∈Σ*。令是Ω上的σ-代数,P是Ω上每个部分都有P0的积测度,则称P是随机共形迭代函数系。
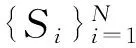
dist(Ei,Ej)≥δmax{|Ei|,|Ej|}
(1≤i≠j≤N)以概率1成立,其中|Ei|表示Ei的直径。注意到Si(E)⊂E,i,j=1,2,…,N,归纳可知,对任意两个互不相容的词σ,τ∈Σ*,有
dist(Eσ,Eτ)≥δmax{|Eσ|,|Eτ|}
(3)
以概率1成立。
对每个τ∈Σ*,记
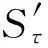
由文献[6]知,存在常数C≥1使对所有的x,y∈E,
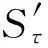
(4)
以概率1成立。这意味着对所有的x,y∈E有
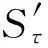
(5)
以概率1成立。
令
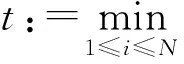
显然0 (6) (7) 以概率1成立。同时,对τ∈Σ*有 (8) 以概率1成立,其中Eτ:=Sτ(E)。 为了证明本文定理,还需要别的记号。定义映射h:Ω×Σ→E为 其中x0∈Rd是任意点。由式(7)知,对ω∈Ω,上述极限存在且不依赖于x0的选取以概率P成立。然后,定义随机变量 (9) 对每个n∈Ν,令 Γn:={τ∈Σ*:Εpτ-≥n-1pmin≥Εpτ}, 易知 定义 同时,令 由文献[4]可知下面的性质。 引理1存在常数M0,λ>0,使对x∈Rd以及ε>0,有 μ(B(x,ε))≤M0ελ (10) 以概率1成立。 证明令 ε0:=δmin{|Ei|:1≤i≤N}。 由文献[5]的引理12.3知,欲证引理1成立,只需证式(10)对x∈E及所有的ε∈(0,ε0)成立即可。 对x∈E及ε∈(0,ε0),存在τ∈Σ*使x∈Eτ,δ|Eτ|≤ε<δ|Eτ-|。因此由式(2)知B(x,ε)∩E⊂Eτ-。从而有 (11) 以概率1成立。 由式(8)及式(6)可知, 以概率1成立。因此 以概率1成立,由式(11)可得, 令 可证引理1成立。 用(A)ε表示A⊂Rd的闭ε邻域。对有限集β⊂Rd及τ∈Σ*,定义 χβ(τ):=card(β∩(Eτ)8-1δ|Eτ|), 则可得引理2。 引理2对任意有限集β⊂Rd,τ∈Σ*,存在常数M≥1,使 (12) 以概率1成立。特别地,如果β⊂(Eτ)8-1δ|Eτ|,那么 以概率1成立。 证明令M:=[(16δ-1+2)d]+1,则Eτ可以被M个中心在其内部,半径为8-1δ|Eτ|的闭球覆盖。可先考虑由中心在Eτ内、半径为16-1δ|Eτ|的闭球组成的Eτ的一个最大覆盖P,然后,把半径扩大2倍得到Eτ的覆盖。通过体积估计知 card(P)(16-1δ|Eτ|)d≤((1+8-1δ)|Eτ|)d。 由式(7)得 以概率1成立。如果β⊂(Eτ)8-1δ|Eτ|,那么 以概率1成立。 推论令α∈Cn(μ),τ∈Σ*,由式(7)可得 以概率1成立。 则有 以概率1成立。 证明参考文献[7]中引理2的证明方法。 引理4对n≥1及常数M0,λ>0,有 证明参考文献[5]中引理5.8的证明方法。 综合上面的引理可以得到定理的证明。 证明定义 N1:=[(16-1δ+6)d]+1, 由引理4,存在最小整数N≥N1+N2,使对k≥N,有 (13) 以概率1成立。N,N1,N2是独立于τ∈Σ*的。对h≤card(Γn),α∈Ch(μ),有 χα(τ)≤N (τ∈Γn)以概率1成立。 假设对某些τ∈Γn,有χα(τ)>N。事实上,由N1,N2的定义可知 1) (Eτ)4-1δ|Eτ|能被N1个中心在此集合上、半径为8-1δ|Eτ|的闭球覆盖,若用γ1表示这个闭球的中心组成的集合,那么card(γ1)=N1。 令γ3∈Cχα(τ)-N1-N2(μ),同时定义 γ:=(α(Eτ)8-1δ|Eτ|)∪γ1∪γ2∪Sτ(γ3), 则card(γ)≤card(α)。再由γ1的定义及度量d的三角不等式,易知3)(见下)。 (14) 以概率1成立。 4) 对x∈Eτ,有 (15) d(x,α)≥8-1δ|Eτ| (16) 均以概率1成立。 由式(15),式(16)及Γn的定义可得 γ)dμ(x)≥Εpτlog (8-1δ|Eτ|)- (17) 以概率1成立。 由引理2,引理3和式(13)可得 (18) 以概率1成立。 联立式(14),式(17)和式(18)可得, 以概率1成立。这显然与α的最优性矛盾。 以概率1成立。因此,由引理4可推得 (19) 以概率1成立。类似地,易证 (20) 以概率1成立。 显然地,对任意x∈Eτ和所有的τ∈Γn, 定义 由式(9)及引理2知,对足够大的n有 (21) 以概率1成立。类似地,可推得 (22) 以概率1成立。综合式(19)至式(22),由性质可证明定理成立。 [1] ZADOR P L. Asymptotic quantization error of continuous signals and the quantization dimension[J].IEEE Trans. Inform. Theory,1982 (28): 139-149。 [2] ARBEITER M,PATZSCHKE N. Random self-similar multifractals[J]. Math. Nachr.,1996 (181): 5-42. [3] DAI M,TAN X. Quantization dimension of randomself-similarmeasures[J]. Math. Anal. Appl.,2010(362):471-475. [4] ZHU S G. The quantization for self-conformal measures with respect to the geometric mean error[J]. Nonlinerarity,2010(23): 2849-2866. [5] GRAF S,LUSCHGY H. Quantization for probability measures with respect to the geometric mean error[J].Math. Proc. Camb. Phil. Soc.,2004 (136): 687-717. [6] PATZCHKE N. Self-conformal multifractal measure [J].Adv. Appl. Math.,1997 (19): 486-513. [7] ZHU S. Quantization dimension of probability measures supported on cantor-like sets[J]. Math. Anal. Appl.,2008 (338): 742-750. 〔责任编辑:卢 蕊〕 Quantizationdimensionofrandomself-conformalmeasureswithrespecttothegeometricmeanerror WANG Chun-min (Basic Courses Department,Zhenjiang Branch of Jiangsu Joint Vocational College,Zhenjiang 212016,China) In the strong separation condition,the thesis mainly studies and proves the quantization dimension of random self-conformal measures with respect to the geometric mean error and it coincedes with the Hausdorfl dimension. random self-conformal measures; Hausdorff dimension; strong separation condition 2015-03-18 王春敏(1982—),女,江苏镇江人,讲师,硕士生,主要从事分形几何研究。 O211.9 :C :1008-8148(2015)03-0061-05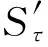
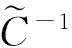
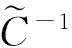
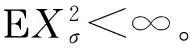
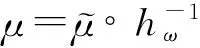
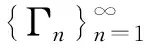
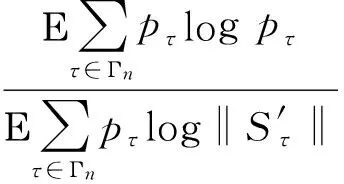
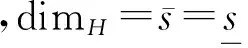
3 定理的证明