左截断右删失数据下Pareto分布形状参数多变点的贝叶斯估计

何朝兵　杜保建　刘华文

摘 要 通过添加缺损的寿命变量数据得到了左截断右删失数据下Pareto分布相对简单的似然函数，给出了形状参数变点位置和其他参数的满条件分布.利用MCMC方法对参数的满条件分布进行了抽样，把Gibbs样本的均值作为参数的贝叶斯估计.随机模拟的结果表明各参数贝叶斯估计的精度都较高.

关键词 似然函数；满条件分布；MCMC方法；Gibbs抽样；Metropolis-Hastings算法

中图分类号 O213.2； O212.8 文献标识码 A 文章编号 1000-2537（2015）03-0080-05

近年来变点问题成为统计学中比较热门的研究方向，它广泛应用于金融、经济和地震预测等领域.目前变点分析方法主要有极大似然法、贝叶斯法和非参数方法等.关于变点问题的研究可参看文献[1-4].而贝叶斯计算方法中的MCMC方法，使变点分析变得非常方便.Pareto分布在生存分析和可靠性理论等方面仍然具有很多应用价值.关于Pareto分布的研究可参看文献[5-7].当进行寿命试验时，经常会出现左截断右删失数据，对此模型的研究可参看文献[8-10].关于左截断或右删失数据下变点问题的研究有一些成果，可参看文献[11-13]，但对数据既左截断又右删失情形下变点问题的研究还不多见.本文主要利用MCMC方法研究左截断右删失数据下Pareto分布形状参数多变点的贝叶斯估计.

1 左截断右删失数据试验模型

设（X，Y，T）是一连续型随机变量，寿命变量X的分布函数为F（x；θ）=P（X≤x），密度函数为f（x；θ），这里θ是未知参数；Y是一右删失随机变量，分布函数为G（y），密度函数为g（y）；T是一左截断随机变量，分布函数为H（t），密度函数为h（t），且Y，T的分布与参

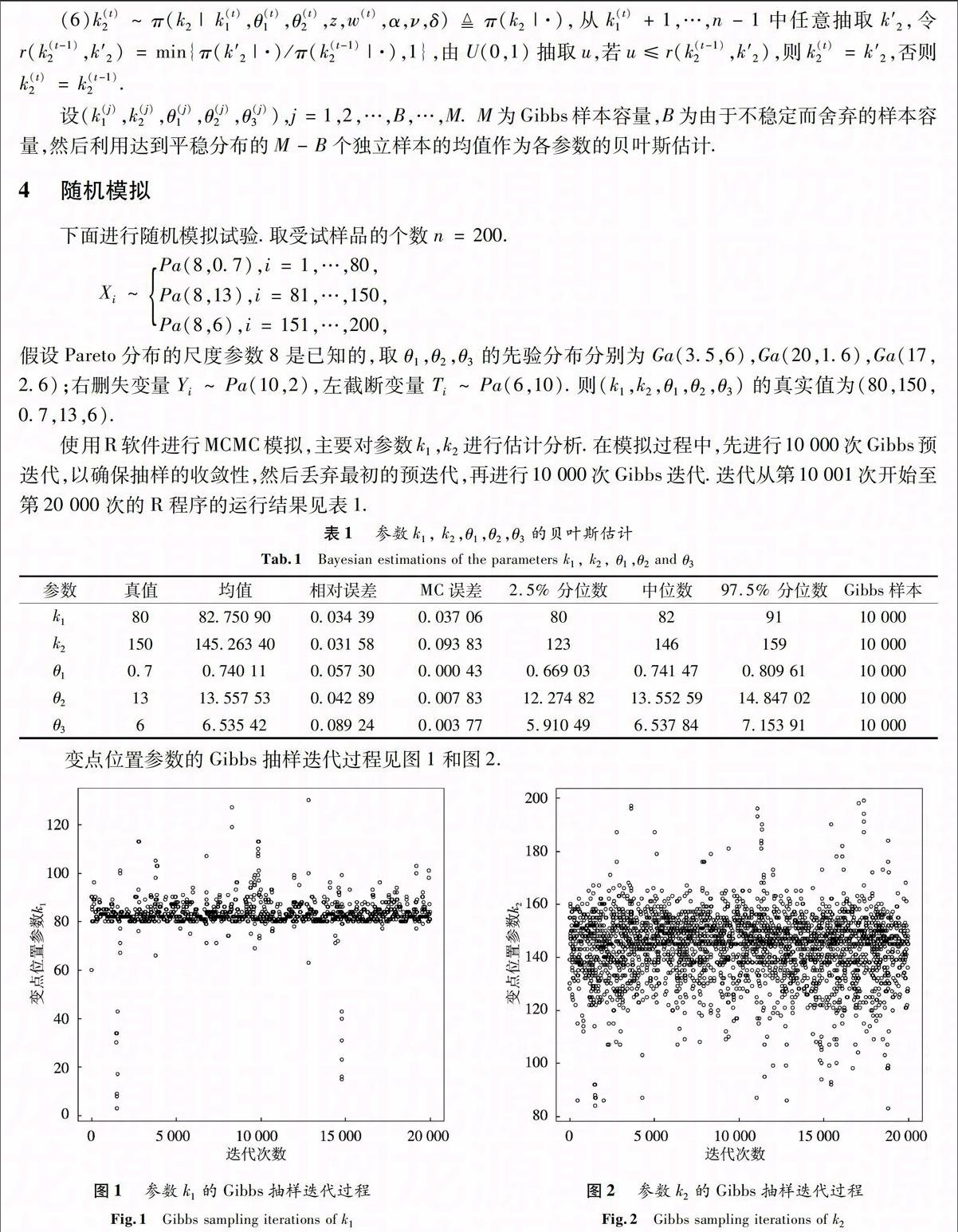
数θ无关.假定X，Y，T是相互独立非负随机变量.对于n个受试样品（产品寿命），左截断右删失数据的试验模型是仅在Zi≥Ti时得到观察数据（Zi，Ti，δi），而在Zi

2 左截断右删失数据下Pareto分布的似然函数

若X的密度函数为f（x）=θbθx-（θ+1），x≥b>0，θ>0，则称X服从尺度参数为b，形状参数为θ的Pareto分布，记为X～Pa（b，θ），易知X的分布函数为F（x）=1-bθx-θ，x≥b.

由（1）式易知，左截断右删失数据下Pareto分布的似然函数比较复杂.

下面添加部分缺损的Xi的值，以获得较简单的似然函数.具体如下：

可以利用筛选法随机产生Z1i的值z1i.z1i抽样的具体步骤如下：

3 左截断右删失数据下Pareto分布形状参数多变点的贝叶斯估计

Pareto分布形状参数多变点模型如下：

Xi～Pa（b，θ1），i=1，2，…，k1，Pa（b，θ2），i=k1+1，…，k2，Pa（b，θ3），i=k2+1，…，n， （3）

其中θ1，θ2，θ3两两不相等，1≤k1

下面利用贝叶斯方法对对变点位置k1，k2及参数θ1，θ2，θ3进行估计.

令D1={1，2，…，k1}，D2={k1+1，…，k2}，D3={k2+1，…，n}.

记β=（k1，k2，θ1，θ2，θ3），由（2）式和（3）式可得此变点问题的似然函数为

其中nm1=n1（Dm），nm2=n2（Dm），sm=s（Dm），m=1，2，3.

下面确定各参数的先验分布.

（1） 对于（k1，k2）取无信息先验分布：π（k1，k2）=1/C2n-1=2[（n-1）（n-2）]-1，1≤k1

（2） 取θi的先验分布为伽玛分布Ga（ci，di），ci，di已知，即

假设（k1，k2），θ1，θ2，θ3相互独立，则

4 随机模拟

下面进行随机模拟试验.取受试样品的个数n=200.

假设Pareto分布的尺度参数8是已知的，取θ1，θ2，θ3的先验分布分别为Ga（3.5，6），Ga（20，1.6），Ga（17，2.6）；右删失变量Yi～Pa（10，2），左截断变量Ti～Pa（6，10）.则（k1，k2，θ1，θ2，θ3）的真实值为（80，150，0.7，13，6）.

使用R软件进行MCMC模拟，主要对参数k1，k2进行估计分析.在模拟过程中，先进行10 000次Gibbs预迭代，以确保抽样的收敛性，然后丢弃最初的预迭代，再进行10 000次Gibbs迭代.迭代从第10 001次开始至第20 000次的R程序的运行结果见表1.

在模型的分析过程中，MCMC的收敛性诊断很重要，模拟时可以对参数进行多层链式迭代分析，即输入多组初始值，形成多层迭代链，当抽样收敛时，迭代图形重合.在模拟过程中，输入两组初始值分别进行10 000次迭代，变点位置参数的多层迭代链轨迹见图3和图4.

最后，进行模拟结果分析.首先，由表1可以看出位置参数的贝叶斯估计与真值的相对误差不超过4%，其他参数估计的相对误差不超过9%，整体上估计的精度较高，效果较好；其次，要判断所产生的马尔科夫链是否收敛，由图3和图4可以发现，变点位置参数的两条迭代链都趋于重合，收敛性较好.综上分析，可以看出通过MCMC方法模拟所产生的效果较好.

参考文献：

[1] PAGE E S. Continuous inspection schemes[J]. Biometrika， 1954，41（1）：100-115.

[2] CSRG M， HORVTH L. Limit theorems in change-point analysis[M]. New York： Wiley， 1997.

[3] CHERNOFF H， ZACKS S. Estimating the current mean of a normal distribution which is subjected to changes in time[J]. Ann Math Stat， 1964，35（3）：999-1018.

[4] FEARNHEAD P. Exact and efficient Bayesian inference for multiple changepoint problems[J]. Stat Comput， 2006，16（2）：203-213.

[5] ARNOLD B C. Pareto distribution[M]. New York： John Wiley & Sons， Inc， 1985.

[6] CASTILLO J， DAOUDI J. Estimation of the generalized Pareto distribution[J]. Stat Probab Lett， 2009，79（5）：684-688.

[7] KAMAL M， ZARRIN S， ISLAM A U. Accelerated life testing design using geometric process for Pareto distribution[J]. Int J Adv Stat Probab， 2013，1（2）：25-31.

[8] BALAKRISHNAN N， MITRA D. Likelihood inference for lognormal data with left truncation and right censoring with an illustration[J]. J Stat Plann Inference， 2011，141（11）：3536-3553.

[9] COSSLETT S R. Efficient semiparametric estimation of censored and truncated regressions via a smoothed self-consistency equation[J]. Econometrica， 2004，72（4）：1277-1293.

[10] GROSS S T， LAI T L. Nonparametric estimation and regression analysis with left-truncated and right-censored data[J]. J Am Stat Assoc， 1996，91（435）：1166-1180.

[11] ANTONIADIS A， GRGOIRE G. Nonparametric estimation in change point hazard rate models for censored data： A counting process approach[J]. J Nonparametr Stat， 1993，3（2）：135-154.

[12] ANTONIADIS A， GIJBELS I， MACGIBBON B. Nonparametric estimation for the location of a change-point in an otherwise smooth hazard function under random censoring[J]. Scand J Stat， 2000，27（3）：501-519.

[13] GIJBELS I， GRLER . Estimation of a change point in a hazard function based on censored data[J]. Lifetime Data Anal， 2003，9（4）：395-411.

（编辑 胡文杰）