带碳费约束的同时取送车辆路径问题研究
2015-07-17段凤华
段凤华


摘 要 在基本车辆路径问题基础上增加“同时取送”、“时间窗”与“碳费”三个约束条件,发展为带碳费约束的有软时间窗同时取送车辆路径问题.建立了相应的数学模型,设计了以Or-opt为邻域结构、增加碳费惩罚机制的禁忌搜索算法对模型求解.通过与相关文献进行比较,显示了禁忌搜索算法搜索速度和寻优能力的优越性.物流企业若能采用以较好算法开发的车辆调度软件,将能削减其碳费,提升自身经济效益和社会效益.
关键词 车辆路径问题;同时取送货;软时窗;碳费;禁忌搜索
中图分类号 TP391 文献标识码 A 文章编号 1000-2537(2015)03-0069-005
在物流配送活动中,同时取送货现象广泛存在,如快递业,既要将快件、包裹送给客户,又要从客户处带回需要寄出的快件或包裹;啤酒行业,销售商需要用车辆将啤酒产品送到客户处,可能同时又需要回收空瓶等等.另一方面,大量车辆行驶在路上,汽车尾气排放过多,已成为全球空气污染加重、特别是诸多地方雾霾弥漫的重要原因.一般而言,在车辆排量既定、路况相似的情况下,运输距离是影响油耗的最主要因素,而油耗是决定车辆碳排放量的关键因素,因此,本文将车辆运输距离转化为碳排放量,进而转化为碳费.在安排车辆行驶线路时,同时考虑碳费,以兼顾配送成本最小化和减少环境破坏,具有理论价值和现实意义.
对有碳排放约束的物流业发展规划,国外研究较多,最近的如文献[1~5],而国内研究较少,但也有个别研究成果,如文献[6~8].
1 带碳排放约束的有软时窗同时取送车辆路径问题描述与数学模型
车辆路径问题(Vehicle Routing Problem,VRP) 是1959年由Dantzig和Ramser提出的[9],本文研究带碳费的有软时窗同时取送车辆路径问题(The Simultaneous Pick-up and Delivery VRP with Soft Time Windows and Carbon Emissions Fee,SPDVRPSTWCEF)是基本车辆路径问题的扩展.SPDVRPSTWCEF是指车辆从配送中心出发,访问客户.客户位置已知、车辆对客户的送货量和取货量都已知、客户所希望的服务时间窗口已知;车辆沿途一边送货一边取货,完成任务后,各车辆把取回的货物送回配送中心;根据车辆在运输中产生的碳排放量对其征收一定的碳费,以促使承运人减少配送活动中的碳排放.车辆在访问各客户时,允许其到达客户开始服务的时间不在客户所要求的时间窗口内,但必须给予相应惩罚;完成任务后,车辆返回车场.问题是如何给每辆车确定其行驶路线,使得在满足装载量和行驶距离限制的条件下,以最少车辆数、最短行驶距离,最小服务时间偏离,以及最少碳费完成规定的货物取送业务.目前,关于SPDVRPSTWCEF的公开文献还不多见,文献[10]研究考虑CO2减排因素的同时取送货车辆路径问题,采用Xpress-MP软件对案例的数学模型进行求解.其他的文献,如[11~13],在研究同时取送货问题时,都没有涉及碳费.对SPDVRPSTWCEF研究成果的应用,将极大地提高物流效率和效益,并将促进物流运输配送优化信息技术产品开发和应用,促进我国低碳物流和整个社会低碳经济的发展.
SPDVRPSTWCEF可以描述为:有1个车场(编号为0),拥有容量为Q的车辆若干辆,负责对n个客户(编号为1,2…,n)进行同时取送货物工作,客户i的货物需求为di,且di≤Q,表示从客户i取回的货物量为pi (目的地为发车场),且pi≤Q,每个客户只能由一辆车服务一次,车辆早于或迟于客户规定的服务时间窗口服务,均须支付一定罚金,车辆须根据其所消耗燃料排放的CO2缴纳碳费.车辆完成任务后,返回车场.
为构造数学模型,定义变量如下.
K表示所需车辆数;Q表示车辆最大载重量;dij表示客户i和客户j的直接距离,假设距离矩阵对称,即dij=dji;di表示送达给客户i的货物量(从发车场发出); qi表示车辆离开客户i时的载重量;Qk表示车辆k离开车场时载重量;ai表示客户i的最早服务时间窗,bi表示客户i的最晚服务时间窗;p1表示车辆到达时间违返最早时间窗时的惩罚系数,p2表示车辆到达时间违返最晚时间窗时的惩罚系数;p0表示碳费率;si表示车辆在客户i的服务时间;ti表示车辆到达客户i的时间;c表示客户单位距离配送成本,客户i的货物由车辆k 配送到则yik=1,否则yik=0;车辆k从客户i行驶到客户j则yijk=1,否则yijk=0;如果客户i和客户j在同一路线且客户j恰好在客户i之后服务,则车辆到达客户j的时间为:tj=ti+si+tij;D表示车辆行驶总距离.
根据问题描述,建立SPDVRPSTWCEF数学模型如下:
模型中,式(1)表示第一优化目标,即最小化车辆数;式(2)表示第二优化目标,即车辆行驶总费用最小(包括距离费用、碳排放惩罚费用、时间窗惩罚费用);式(3)表示车辆k离开车场时载重量;式(4)表示车辆行驶距离限制;式(5)表示第k条路线从车场出发后,离开第一个客户点时的载重量;式(6)表示客户i和客户j在同一路线且客户j恰好在客户i之后服务时,车辆k离开客户j时的载重量;式(7)、(8)和(9)表示受车辆载重量的限制,车辆在取送作业过程中不能超出其载重量;式(10)表示K辆车都从配送中心出发,最后又回到配送中心;式(11)表示每个客户只由一辆车配送且所有客户都得到服务.
2 禁忌搜索算法设计
禁忌搜索算法是对局部邻域搜索的一种扩展,是一种全局逐步寻优的智能和通用启发式算法.本算法将以随机方式产生初始解.
2.1 邻域结构
为了进一步增强禁忌搜索算法的机能,以便能在减少所使用的车辆数和车辆行驶费用两个方面都能得到更好的改进.本文使用Or[14]提出Or-opt方法,该方法是将一段路径(1个、2个、3个连续的顶点)在另外两个顶点间重新定位,相当于一个受约束的3-opt交换.Or-opt方法是k-opt中的一种,k-opt通过每次交换条边来改进初始解.对于k=2,3……,Lin[15]等人从大量计算中发现,3-opt最优算法比2-opt好,而4-opt最优算法并不比3-opt最优算法好多少,而且k越大,计算量增大速度越快,运算时间越长.本文根据Or-opt将一段路径(1个、2个、3个连续的顶点)在另外两个顶点间重新定位,设计了Or-opt-1,Or-opt-2,Or-opt-3三种交换的组合,以随机的方式选择其中一种应用于当前解.下面对可行变换进行说明,其中带下划线者为所挑选的顶点.在同一线路或不同两条线路中随机挑选两个顶点(客户点或车场),随机执行下列3种变换之一.
1) Or-opt-1,将一条路径中1个顶点在另一条路径中两个顶点间重新定位,例如:
X1=(012340567089)→X1=(012405637089).
2) Or-opt-2,将一条路径中2个顶点在另外一条路径中两个顶点间重新定位,例如:
X1=(012340567089)→X1=(012056347089).
3) Or-opt-3,将一条路径中3个顶点在另外两个顶点间重新定位,例如:
X1=(012340567089)→X1=(012563407089).
2.2 解的评价
SPDVRPSTWCEF类型的车辆调度问题有两个需要优化的目标:所使用的车辆数和最低总配送费用(指行驶费用、偏离时间窗的惩罚和碳费).最小化所使用的车辆数是第一层优化目标,具有较高的优先权.为了充分对解空间进行搜索,算法接受导致不可行解的变换.违反了车辆装载能力和最大行驶距离限制时,其不可行性的程度可以通过引入一个惩罚值而将该约束条件包含到目标函数中去进行度量,即
∑Kr=1{T(r)+ET(r)+p[E(r)+L((r)]+c(r)}.
其中K是该解中所使用的车辆数(线路数);T(r)为车辆r的行驶费用;ET(r)为在线路r上早于或晚于时间窗卸下的部分;c(r)为碳费;E(r)为在线路r上超出车辆载重量的部分;L(r)为在线路r上超出车辆行驶距离的部分;而p是惩罚系数.若一个解是可行的,则所有线路上的E(r)都等于零.p∈[0.000 01,200 000]开始时等于1,并通过一个自调整参数来加权:每隔10次迭代测试一次,若前面的10个解都是可行的,则将其除于2;若所有的10个解都是不可行的,则将其乘于2.这种机制可以产生一种可行解和不可行解的混合,有利于减少陷入局部最优的可能性[16].
2.3 禁忌表与终止准则
2.3.1 禁忌表 禁忌表用于记载在最近的10次迭代中解的变换特征.可以构造一组(n+1)×(n+1)阶矩阵来记录禁忌情况.若点i 和 j 被挑选来进行以下三种变换:Or-opt-1,Or-opt-2,Or-opt-3三种交换,则将其禁忌情况存入矩阵的元素(i,j)中.在每一次迭代时,都必须将上一步所进行的变换填入到禁忌表中,而表中的其他元素相应地减1直到等于零为止.
2.3.2 终止准则 当总迭代次数达到一个给定值,或在给定的连续迭代步数内当前最好解没有改变时,则算法终止.
3 算例分析
本算法已用Delphi语言编程,并在Pentium-Ⅳ 2.67 GHz微机上实现.目前,对于本文研究的带碳费约束的车辆路径问题,国际上还没有统一的标准测试数据,为了方便对比分析,为了测试算法的计算效果,本文使用文献[12]和[17]中的算例,客户点数据表见表1,车场坐标为(3.2,14.1),配送中心有若干辆载重量均为8 t的车,车辆最大的行驶距离为50 km,车辆行驶速度为20 km/h,每公里配送成本为1 元/h,为了提高客户的满意度,车辆早到在该客户点等待,车辆晚于时间窗口服务则惩罚系数(p2)为6 元/h,没有考虑服务时间(si=0).需要优化的目标:最小化所需车辆总数,最小化总配送费用.碳费计量方面,为了简化问题,参照澳大利亚政府CO2排放税拟征收标准(23澳元/t,约相当于人民币160元),定为0.16 元/kg CO2;载重量8 t的车百公里油耗约为20 L,根据BP中国碳排放计算器提供的资料,1 L柴油排放2.63 kg CO2,所以每百公里碳排放惩罚系数=20×2.63×0.16=8.416(元).
本算法对文献[17]单向取货与送货问题求解,计算10次取最优解如表2所示,单向取货问题与送货问题目标函数值比文献[17]节省的比率分别了1.89%和2.92%.
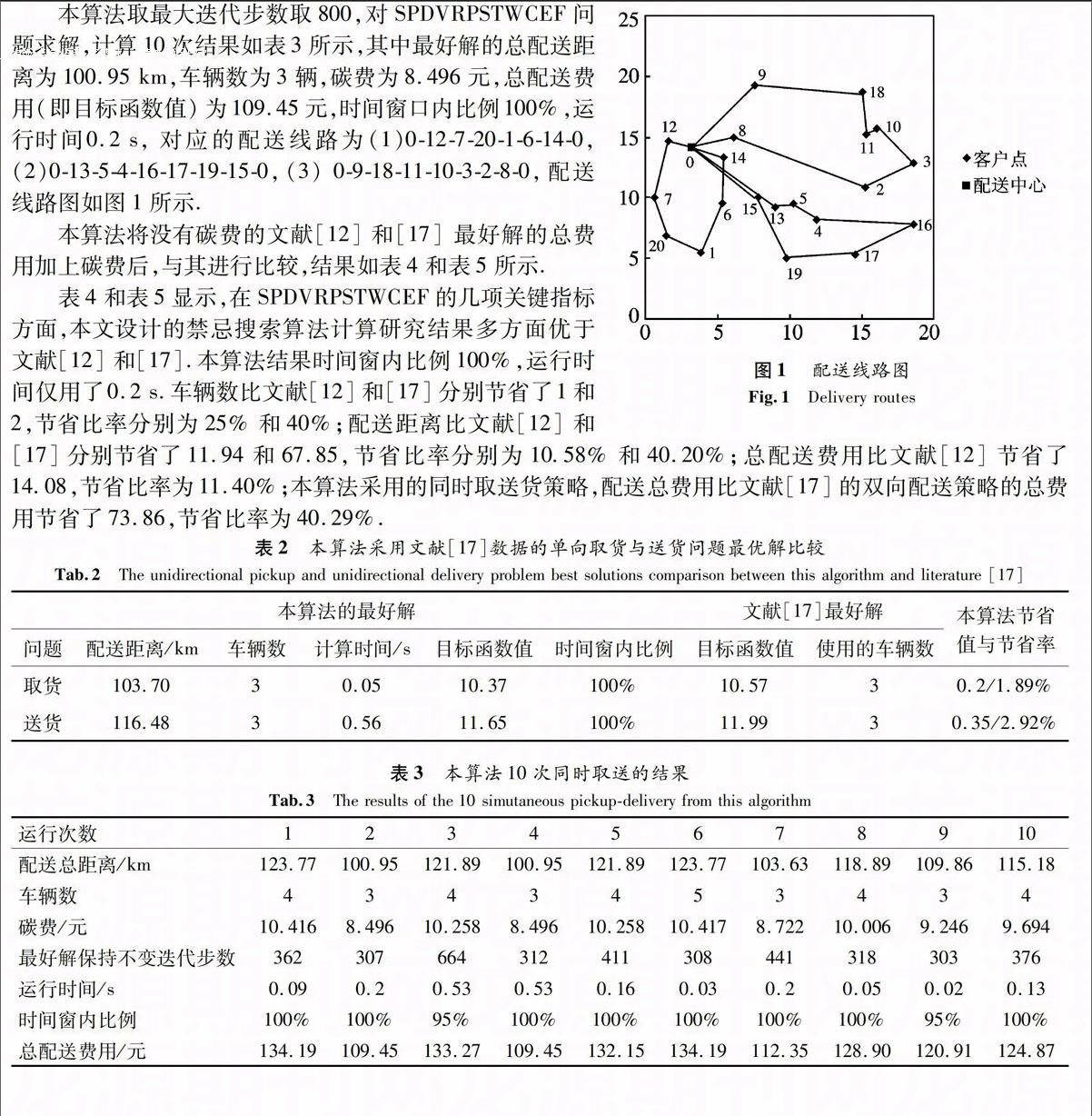
本算法取最大迭代步数取800,对SPDVRPSTWCEF问题求解,计算10次结果如表3所示,其中最好解的总配送距离为100.95 km,车辆数为3辆,碳费为8.496元,总配送费用(即目标函数值)为109.45元,时间窗口内比例100%,运行
时间0.2 s,对应的配送线路为(1)0-12-7-20-1-6-14-0,(2)0-13-5-4-16-17-19-15-0,(3) 0-9-18-11-10-3-2-8-0,配送线路图如图1所示.
本算法将没有碳费的文献[12]和[17] 最好解的总费用加上碳费后,与其进行比较,结果如表4和表5所示.
表4和表5显示,在SPDVRPSTWCEF的几项关键指标方面,本文设计的禁忌搜索算法计算研究结果多方面优于文献[12]和[17].本算法结果时间窗内比例100%,运行时间仅用了0.2 s.车辆数比文献[12]和[17]分别节省了1和2,节省比率分别为25%和40%;配送距离比文献[12]和[17]分别节省了11.94和67.85,节省比率分别为10.58%和40.20%;总配送费用比文献[12]节省了14.08,节省比率为11.40%;本算法采用的同时取送货策略,配送总费用比文献[17]的双向配送策略的总费用节省了73.86,节省比率为40.29%.
5 结论
通过对SPDVRPSTWCEF进行定义和描述,本文建立了SPDVRPSTWCEF数学模型.通过以随机方式产生初始解、有3种Or-opt交换组合可随机选择一种应用于当前解、引入罚值对解进行评价,设计了求解问题的禁忌搜索算法.与同类文献的比较显示,本文算法能得到较好的计算结果,计算效率也较高.说明采用同时取送货的策略优于双向配送策略,物流企业在采用好的算法开发的软件进行车辆调度的情况下,企业能减少碳排放;即使征收一定的碳费,企业仍能增加收益.因此,应该鼓励企业将新技术应用于管理,以促进低碳物流,同时提高企业运营效率和经济效益.
参考文献:
[1] BEHNAM F, MOHSEN R, TUPAN P, et al. The implications of carbon pricing in Australia: An industrial logistics planning case study[J].Trans Res Part D: Trans Environ, 2013,18(1):78-85.
[2] STEPHANIE S. Policy in motion: reassembling carbon pricing policy development in the personal transport sector in British Columbia[J].Trans Geography, 2011, 19(6):1474-1481.
[3] GEORGINA S HANNAH B, LAURA M, et al. Externalities and economic policies in road transport[J].Res Trans Econ, 2010,28(1):2-45.
[4] KIM S T, HAN C H. Measuring environmental logistics practices [J].Asian Shipping Logist, 2011,27(2):237-258.
[5] FEDELE I. The private and social cost efficiency of port hinterland container distribution through a regional logistics system[J]. Trans Res Part A: Policy and Practice, 2012,46(9):1424-1448.
[6] JIANG B, LI J, MAO X Y. Container ports multimodal transport in China from the view of low carbon [J]. Asian Shipping Logist, 2012,28(3):321-343.
[7] LI J, LIU X, JIANG B. An exploratory study on low-carbon ports development strategy in China [J]. Asian Shipping Logist, 2011,27(1):91-111.
[8] YANG J H, GUO J D, MA S G. Distribution network design for carbon tax-constrained urban cold Chain logistics [J]. Ind Eng, 2012,15(5):86-91.
[9] DANTZIG G, RAMSER J. The truck dispatching problem[J]. Manag Sci, 1959,2(6):80-91.
[10] 史春阳.同时取送货的车辆路径问题中的低碳研究[D].北京:清华大学, 2011.
[11] 潘立军. 求解带软时间窗取送化问题的遗传算法[J].系统工程理论与实践, 2012,32(1):120-126.
[12] 关丽霞.带软时间窗和同时取送货的车辆路径问题研究[D].长沙: 中南大学, 2010.
[13] 陈 萍,黄厚宽,董兴业. 求解卸装一体化的车辆路径问题的混合启发式算法[J]. 计算机学报, 2008,31(4):565-573.
[14] OR I. Traveling salesman-type combinatorial optimization problems and their relation to the logistics of regional blood banking: [D]. Evanston, IL: Northwestern University, 1976.
[15] LIN S. Computer solutions of the traveling salesman problem[J]. Bell Syst Tech J, 1965,44(1):2245-2269.
[16] 符 卓. 带装载能力约束的开放式车辆路径问题及其禁忌搜索算法研究 [J].系统工程理论与实践, 2004,24(3):123-128.
[17] 朗茂祥. 物流配送车辆高度问题的模型和算法研究[D].北京:北京交通大学, 2002.
(编辑 陈笑梅)
