例谈如何让学生经历数学学习的探究历程
2015-07-14陈华锋
陈华锋
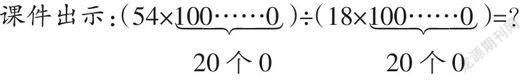

[摘 要]教师要引导学生独立思考、主动探究、合作交流,呈现一个充满生命活力的学习探究过程,从而促进学生理解和掌握基本数学知识与技能,体会和运用数学思想与方法,获得基本的数学活动经验。以“商的变化规律”一课为例,从“激发学生探究欲望、搭建学生探究平台、分享学生探究成果、提升学生探究能力”四个维度进行思考与实践,改变以往以教师为中心的教学方式,真正让学生成为学习的主人。
[关键词]商的变化规律 探究 时间和空间
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2015)08-068
课程标准明确指出:学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。然而,仍有不少教师在课堂教学中,轻过程、重结果,忽视知识的形成过程,忽略学生对新知的认知过程,让学生机械重复地去做习题,与新课程教学理念背道而驰。如何让学生有足够的探究时间与空间,真正经历数学学习的探究历程?下面以“商的变化规律”一课为例,谈谈我的思考与实践。
一、激发学生探究欲望,让学生主动探究
学生学习应该是一个生动活泼的、主动的和富有个性的过程。只有激发学生的探究欲望,激发学生挑战的斗志,激活学生的知识潜能与内驱力,才能促使学生去观察、去思考、去分析,自主探究的意识也就随之萌发与滋长。
【教学片段一】
课件出示:(54×■)÷(18×■)=?
20个0 20个0
师:谁能说出得数是几?(学生面露难色)
生1:等于2。
生2:可能等于3。
师:能说说为什么等于3吗?
生3:可以把它看成54÷18=3。
生4:可以从小数字开始研究,找找规律。
师:是不是等于3呢?和54÷18=3是不是有联系呢?学习了这节课的知识后你们就会明白其中的规律。
以“54÷18”为中心,把被除数和除数巧作变化,为新知的探索创设了学习情境,有利于激发学生探究的欲望。长此以往、坚持不懈,学生就会形成持久的学习内驱力。
二、搭建学生探究平台,让学生成为探索者
教师在教学活动中要根据学生的心理特点,增设活动素材,为他们搭设一个开放的具有挑战性的探究平台,尽量多给学生一点思考的时间,多给学生一次展现自己的机会,多给学生一份探究的空间,使课堂教学活动真正成为学生自主学习和探索的天地。
【教学片段二】
1.课件出示:计算下面各题,你有什么发现?
(54×2)÷(18×2)= (54÷6)÷(18÷6)=
(54×3)÷(18×3)= (54÷9)÷(18÷9)=
(54×5)÷(18×5)= (54÷18)÷(18÷18)=
我的发现:
2.小组交流自己的计算结果与发现。
3.全班汇报。
生1:商都等于3。
生2:被除数54乘一个数,除数18也要乘一个数,商还是3。
生3:被除数54乘一个数,除数18也要乘同一个数,商还是3。
生4:除以也可以。
生5:右边被除数54除以一个数,除数18也要除以同一个数,商还是3。
生6:被除数和除数都乘一个相同的数,商不变。
生7:被除数和除数都除以一个相同的数,商不变。
生8:被除数和除数都乘或除以一个相同的数,商不变。
师:说得真好,把掌声送给他们。
……
师:大家发现的这个规律真的正确吗?也许这个规律只适用于“54÷18”呢?我们要确认这个规律,还需要干什么?
生9:需要进一步验证其他的除法算式里是否也存在这样的规律。
师:谁能举几个例子来进行验证?
生10:(32×5)÷(8×5)=4,(32÷4)÷(8÷4)=4。(板书)
生11:(72×2)÷(9×2)=8,(72÷9)÷(9÷9)=8。(板书)
……
师:你们不但会发现规律,还能进一步验证规律。我也来举两个例子(54×0)÷(18×0)=0和(54÷0)÷(18÷0)=0(板书),好像商发生了变化,难道前面的规律错啦?
生12:除数不能等于0。
师:那刚才得出的规律还需加上一个什么条件?
生13:0除外。
生14:被除数和除数都乘或除以一个相同的数(0除外),商不变。
师:太完美了,把掌声送给她。
继续以“54÷18”为中心,把被除数和除数作出相应的系列变化,分为同乘和同除(以)两种情况,刻意地改变了教材里表格式填数的呈现方式,为学生提供了简洁、明了的探究材料,有利于学生观察和思考,学生精妙绝伦的回答就是最好的例证。只有为学生提供适合的、开放的、具有一定挑战性的探究平台,才能使学生有思索的空间,促使学生智慧火花的迸发。
三、分享学生探究成果,让学生体验成功
心理学研究表明:活动中成功的体验,会让学生产生积极学习并再次体验成功的需要。因此,给学生提供深入思考的机会,让学生拿研究得出的结论去解决学习中的疑惑,能使学生感悟到数学学习的价值所在,从而获得成功的快乐与喜悦。
【教学片段三】
师:回过头来看,(54×■)÷(18×■)等于多少呢? 20个0 20个0
生1:等于3。(学生异口同声地回答,情绪高涨)
师:能说说为什么吗?(几乎全班学生都举起了手)
生2:被除数和除数都乘一个相同的数,可以看成“54÷18”来计算,等于3。
顺延“54÷18”这条主线,在引导学生观察,初步得出规律后,举例进行验证,任意更换相除两数和或乘或除以同一个数,为学生提供了更为深入思考的契机。当教师举出例子进行验证时,学生马上明白还缺少一个必要条件,从而完整地得出商不变的规律,并应用规律解决了课始的难题。当学生通过独立思考,经历了探索全过程,解决了新奇而富有挑战的数学问题后,就能从中体验到一种成功感,从而走向想探索、爱探索、乐探索的漫漫求知之路。
四、提升学生探究能力,让学生自主发展
探究能力,是一种综合的学习能力,是一种科学的精神,也是一种意识。在经历了一个完整的探究历程以后,需要师生一起回顾自己的探究历程,积累探究的基本策略与活动经验,总结探究的基本方法,不断提升学生的探究能力,从而促进学生的自主发展。
【教学片断四】
师:今天我们是怎样学习的?主要经历了哪几个步骤?
生1:我们开始遇到了困难,学会退,从小数字开始研究。
生2:我们通过举例、计算、观察、发现了规律。
生3:我们还验证了规律、应用了规律解决问题。
师生一起小结:
策略:遇到难——退,退回原点——容易
方法:举例——计算、观察——发现规律——验证规律——应用规律
师:这是非常好的一种探究学习的策略,大家可以在以后的学习中经常运用。
教学活动应是教师引导学生不断探究,获取新知的过程,要改变以往以教师为中心的教学方式,真正让学生成为学习的主人,多给他们探索、思考、交流的时间和空间,使学生乐于探索、敢于探索,从而深深爱上探索。
(责编 金 铃)
