EEMD在同时消除脉搏血氧检测中脉搏波信号高频噪声和基线漂移中的应用
2015-07-12韩庆阳王晓东李丙玉周鹏骥
韩庆阳王晓东 李丙玉 周鹏骥
(中国科学院长春光学精密机械与物理研究所光电技术研发中心 长春 130033)
EEMD在同时消除脉搏血氧检测中脉搏波信号高频噪声和基线漂移中的应用
韩庆阳*王晓东 李丙玉 周鹏骥
(中国科学院长春光学精密机械与物理研究所光电技术研发中心 长春 130033)
人体血氧饱和度是基于脉搏波信号测量得到的,然而在脉搏波信号采集的过程中存在着由人体呼吸和仪器本身热噪声等带来的基线漂移和高频噪声,影响人体血氧饱和度的测量精度。因此,该文提出一种总体平均经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)与基于排列熵(Permutation Entropy, PE)的信号随机性检测相结合的方法,同时消除基线漂移和高频噪声。对脉搏波信号进行EEMD分解,计算分解到得到的内在模式分量的排列熵,选取阈值,分别判断并剔除代表高频噪声和基线漂移的内在模式分量。最后信号重构就得到同时消除高频噪声和基线漂移的脉搏波信号。通过自行研制的测量装置所采集的脉搏波信号进行实验验证,利用信号的频谱和交直流比R评价效果。结果表明:该方法有效地同时消除了脉搏波信号中的高频噪声和基线漂移,这将有利于人体血氧饱和度测量精度的提高。
脉搏波信号;人体血氧饱和度;高频噪声;基线漂移;总体平均经验模态分解;排列熵
1 引言
人体血氧饱和度是衡量人体血液含氧量的重要参数,它是利用人体动脉的搏动引起血液的吸光度变化,结合朗伯-比尔定律计算得到的[1]。通过借助光电手段测量得到动脉血液的吸光度变化即为人体的脉搏波信号。
由于脉搏波信号十分微弱,因此,测量得到的脉搏波信号极容易受到干扰,这些干扰主要有3种,分别是:运动伪差、高频噪声和基线漂移[2−4]。其中,运动伪差是由测量部位和测量装置之间的相对运动引起的;高频噪声则是信号采集过程中仪器的热噪声和电磁干扰等;基线漂移是被测对象的生理活动,如:呼吸和咳嗽等,是一种低频噪声[5,6]。这些干扰影响测量得到的脉搏波信号质量,进而影响最终人体血氧饱和度的测量精度。本文主要讨论高频噪声和基线漂移的消除方法。
对于脉搏波信号中的高频噪声和基线漂移的消除方法通常有:多项式插值、小波变换和经验模态分解(Empirical Mode Decomposition, EMD)等[7−9]。多项式插值需要确定“基准点”;小波变换需要确定分解层数和小波基函数;经验模态分解存在模态有混叠。总体平均经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)是一种改进的EMD法[10−12],通过向待处理信号中加入高斯白噪声,多次EMD分解后得到IMF(Intrinsic Mode Function)平均分量,解决了EMD分解的模态混叠的问题,并且不需要确定分解层数和选择基函数;排列熵(Permutation Entropy, PE)是一种检测时间序列的随机性和动力学突变的方法,具有概念简单,运算速度快,抗干扰能力强等特点[13,14]。因此,本文提出将EEMD与基于排列熵的信号随机性相结合的方法,同时消除脉搏波信号中的高频噪声和基线漂移。
2 算法原理与步骤
2.1 算法原理
首先对由人体血氧饱和度测量装置采集的含有高频噪声和基线漂移的脉搏波信号进行EEMD分解;计算分解得到的IMF分量的排列熵,设置阈值判断出代表高频噪声和基线漂移的IMF分量;将代表高频噪声的IMF分量置零,代表基线漂移的IMF分量取均值;然后信号重构就得到消除高频噪声和基线漂移的脉搏波信号。该方法的优点在于处理过程简便,有可靠的判据作为依据,有用信号损失小。
算法的具体原理如下:
在原始信号中添加白噪声,则信号变为

其中,ci白噪声的幅值,白噪声的标准差一般为原始信号的0.1~0.2倍,对信号进行EMD分解,然后重复添加幅值为ci的白噪声再分解,如此重复d次,一般取d=100~200。则信号可以表示为
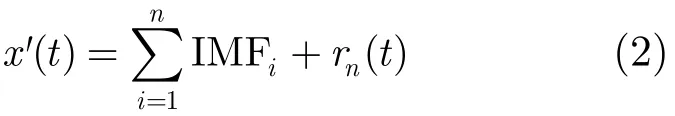
式中,i为整数,1≤i≤n,rn(t)为余项,IMF1~IMFn为分解得到的IMF分量,对每个长度为N的IMF分量进行空间重构得到如下序列:

其中1≤h≤N−(α−1)λ, α是嵌入维数,λ是时间延迟,将IMFi(h)的α个向量IMFi(h)={IMFi(h), IMFi(h+λ),…,IMFi(h+(α−1)λ)}按照升序排列,即
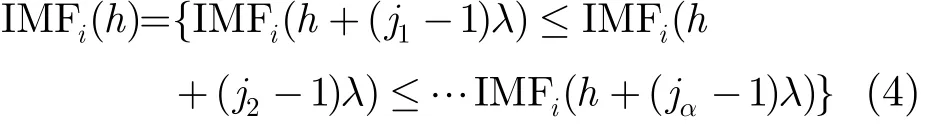
若IMFi(h+(jh1−1)λ)=IMFi(h+(jh2−1)λ),则按照j的大小进行排列,所以,任意IMF分量都可以得到一组符号序列S(g)={j1,j2,…,jm},其中g=1, 2,…,h,h≤α!。α个不同的符号{j1,j2,…,jm}有α!种排列,S(g)是α!种符号的一种。计算每种符号出现的概率Pg,概率的和为1。
IMF分量的排列熵为
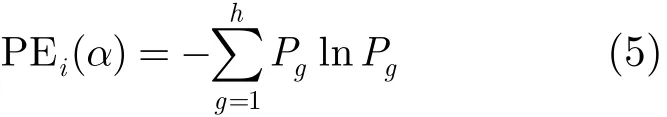
当Pg=1/α时,PEi(α)达到最大值ln(α!),将PEi(α)通过ln(α!)标准化处理后得

所以信号分解后的IMF分量IMFi的排列熵为PEi(i为整数,1≤i≤n),在计算排列熵时需要确定嵌入维数α和时间延迟λ,根据经验值一般取作α=6, λ=1;PEi值越大说明该IMF分量越随机,反之说明越规则。确定排列熵的阈值,判断出代表高频噪声的IMF分量为IMF1~IMFm(m为整数,1≤m≤n ),代表基线漂移的IMF分量为IMFp~IMFm(p为整数,1≤p≤n);则基线为式中k为整数,p≤k≤n,将代表高频噪声的IMF置零,代表基线漂移的IMF分量取均值,信号重构得到x(t)'': l≤m≤p, m≤l≤n。

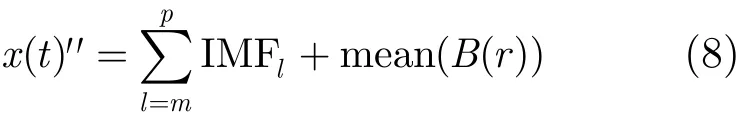
2.2 算法步骤
首先,采集脉搏波信号,对含有高频噪声和基线漂移的数据添加白噪声如式(1);其次,对添加白噪声的脉搏波信号进行EEMD分解得到式(2);然后根据式(3)、式(4)、式(5)和式(6)计算每个IMF分量的PE值;再通过经验选取PE的阈值,判断代表高频噪声和基线漂移的IMF分量,通过式(7)得到基线漂移;最后通过式(8)得到同时消除高频噪声和基线漂移的脉搏波信号。
式中,mean(B(r))为将B取平均即为消除干扰后的基线,r为采样点,p,m和l为整数,且1≤p≤n,
3 实验
利用自行研制人体血氧饱和度测量装置采集脉搏波信号,验证该方法对高频噪声和基线漂移的消除效果,图1是该装置的框图。
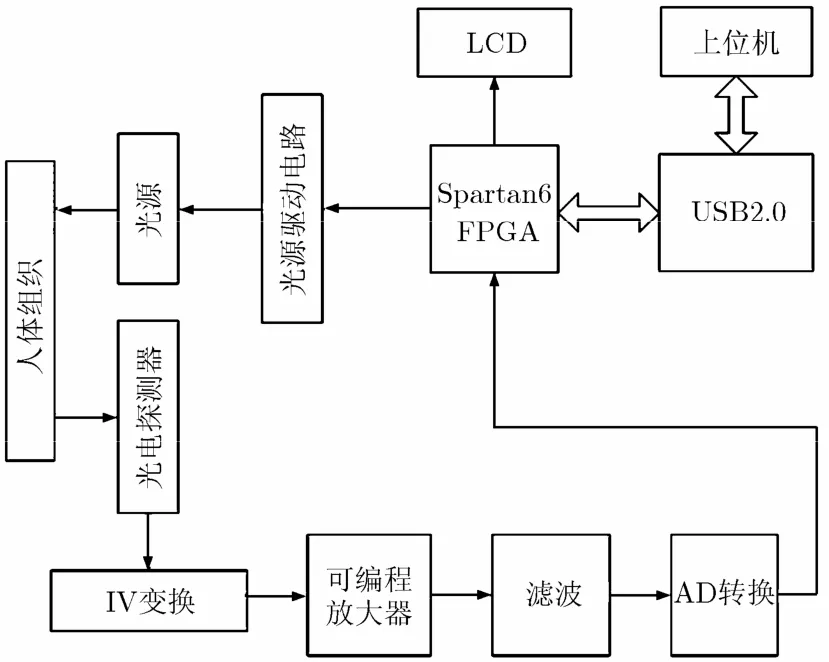
图1 人体血氧饱和度测量装置框图
以Xilinx公司生产的Spartan 6系列FPGA为核心,其工作时钟为100 MHz,满足脉搏波信号的采集速度要求:脉搏波信号的采样率为200 Hz。首先,通过光源驱动器驱动LED光源发光,然后再由光电探测器将人体动脉搏动引起的光信号变化转换成电信号,在进入微控制器前对信号进行IV变换、程控放大、滤波和AD转换等一系列初步处理,再由FPGA将人体脉搏波信号通过基于CY7C68013的USB2.0接口传到上位机,上位机完成人体脉搏波信号的分析处理等工作,将计算后的血氧饱和度再传回FPGA, FPGA通过LCD将血氧饱和度实时地显示出来;当然,也可以在FPGA完成相应的数据处理,但是只靠FPGA计算得到的血氧饱和度相对由上位机计算得到的血氧饱和度精度要低很多;在此,是通过上位机对数据处理计算的。
图2(a)是采集得到的脉搏波信号,脉搏波信号的采样率为200 Hz,由图可以看出:原始信号受到基线漂移和高频噪声的影响;其中,采样点600附近的高频噪声幅值最高,而基线漂移近似正弦波。
图2(b)是经过EEMD分解得到的IMF分量及原始信号,从图中可以初步看出:IMF1~IMF5可能是代表高频噪声的IMF分量,IMF6~IMF9可能代表有用信息,即:脉搏波信号的IMF分量,IMF10~IMF11则可能是代表基线漂移的IMF分量;将它们依次累加就是原始脉搏波信号。但是,只凭借主观判断是不准确的,会带来误差,需要一种数学判据,即:排列熵。
表1是各IMF分量的排列熵,从表1可以看出,排列熵是依次减小的,一般白噪声的排列熵为0.9,属于间歇性信号的噪声,其排列熵大于0.6,正弦信号的排列熵0.2[15]。基线漂移属于低频信号,其随机性相对脉搏波信号差,故其排列熵要小。本文分别测量了50次脉搏波信号进行试验,每次选取排列熵的阈值,阈值的下限和上限的选取的概率分布;其中,阈值下限分布在0.110左右的次数33次,阈值上限分布在0.145~0.155的次数为43次。故本文选取排列熵的阈值范围:0.110≤PE≤0.150;IMF1~IMF5是代表高频噪声的IMF分量,IMF6~IMF9代表有用信息,即:脉搏波信号的IMF分量,IMF10~IMF11则是代表基线漂移的IMF分量。
4 实验结果及分析
4.1 实验结果
图3是原始信号与消除噪声后的信号的对比图,从图中可以看出:消除噪声后的信号比原始信号更光滑,并且原始信号中的基线漂移得到了消除,为了更客观地对算法消除高频和基线的效果进行评价,本文采用信号的频谱和交直流比R分别评价高频噪声和基线漂移的消除效果。
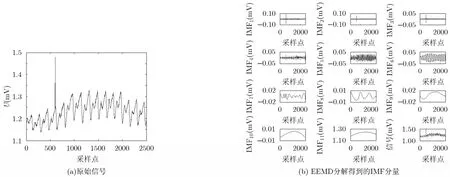
图2 原始信号(a)及EEMD分解得到的IMF分量(b)
4.2 实验结果分析
图4(a), 4(c)是滤波前和滤波后信号的频谱对比图,由图中可以看出,在37 Hz附近的噪声幅值较大;图4(b), 4(d)是滤波前和滤波后信号的频谱在20~100 Hz处的局部放大对比图,由可见滤波后频率在20~100 Hz的噪声被滤除。
基线漂移影响脉搏波信号的稳定性,而脉搏波信号的稳定性则可用信号的交直流比R来衡量,人体在一段时间内脉搏波变化接近恒定,所以R值应趋于稳定。分别计算原始信号和去噪后的信号的R值,如图5所示。图5中横坐标为光电容积脉搏波PPG(PhotoPlethysmoGram)序号。从图5可以明显看出,信号处理后的R值更为稳定,脉搏波信号的基线漂移得到了很好的抑制。
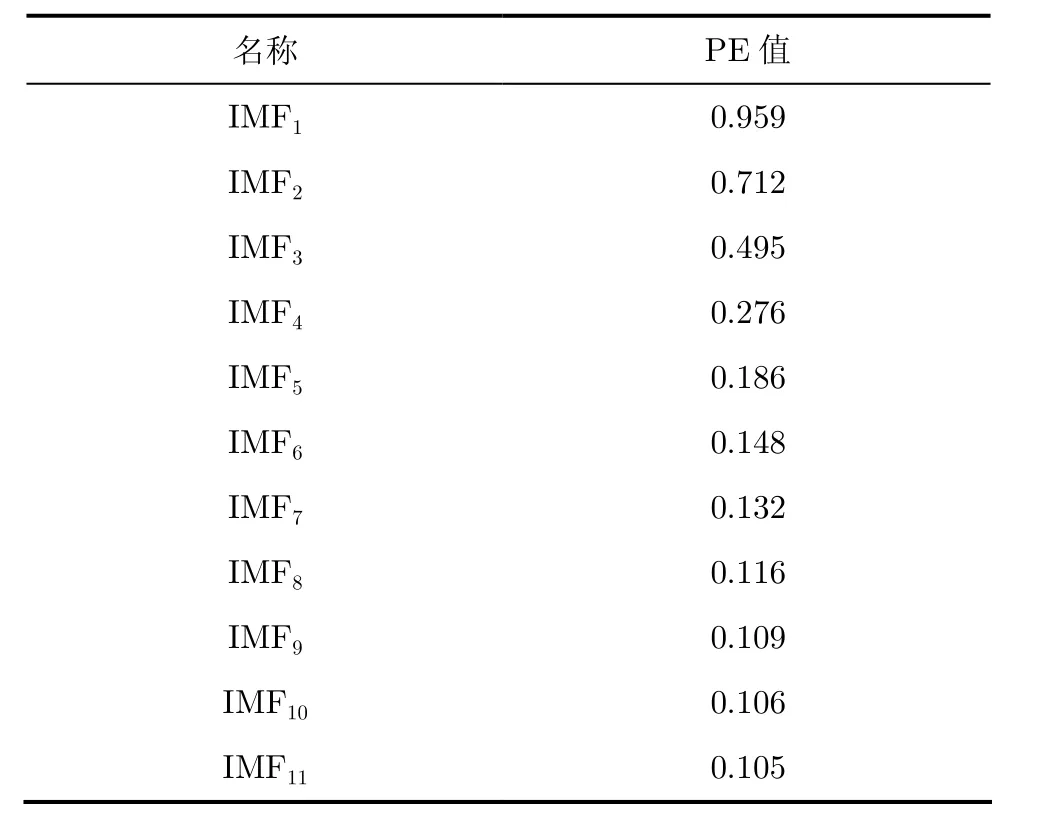
表1 各IMF分量的排列熵

图3 原始与去噪后的脉搏波信号

图4 滤波前后的信号频谱及其局部放大图
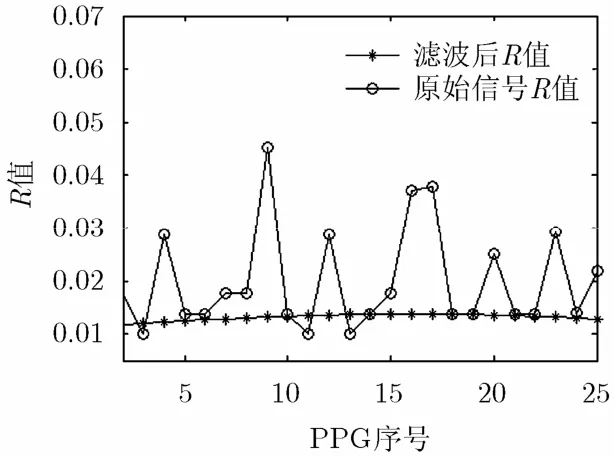
图5 滤波前后信号的R值
5 结论
本文提出一种将EEMD与排列熵相结合的方法同时消除脉搏波信号中高频噪声和基线漂移。该方法是根据信号自身的特点,自适应地将信号分解,无需参数设置,又克服了EMD分解的模态混叠问题;同时排列熵的使用为模态属性判断提供了判据,避免因主观判断造成的误差。该方法在自行研制的人体血氧饱和度检测装置中得到验证,实验证明:该方法有效地同时消除了脉搏波信号中的高频噪声和基线漂移,对人体血氧饱和度检测精度的提高起到了重要作用。
[1] 刘广伟, 毛陆虹, 谢生, 等. 一种光电反射式脉搏血氧检测方法[J]. 光电子⋅激光, 2014, 25(3): 620-624.
Liu Guang-wei, Mao Lu-hong, Xie Sheng, et al.. A monitoring method of blood-oxygen saturation using reflection type photoelectric sensor[J]. Journal of Optoelectronics⋅Laser, 2014, 25(3): 620-624.
[2] 韩庆阳, 李丙玉, 王晓东. 一种消除脉搏波信号中呼吸基线漂移的方法[J]. 中国医疗器械杂志, 2014, 38(1): 19-22.
Han Qing-yang, Li Bing-yu, and Wang Xiao-dong. The method of removing breathing baseline in pluse wave signal[J].Chinese Journal Medical Instrumentation, 2014, 38(1): 19-22.
[3] 韩庆阳, 李丙玉, 王晓东. 一种同时消除脉搏波信号中呼吸基线漂移和高频噪声的方法[J]. 中国医学物理学杂志, 2014, 31(2): 4801-4805.
Han Qing-yang, Li Bing-yu, and Wang Xiao-dong. The method of simultaneously removing breathing baseline and high-frequency noise in pluse wave signal[J]. Chinese Journal of Medical Physics, 2014, 31(2): 4801-4805.
[4] 韩庆阳, 李丙玉, 王晓东. 基于小波变换的脉搏波信号高频噪声与呼吸基线的同时消除[J]. 北京生物医学工程, 2014, 33(6): 247-252.
Han Qing-yang, Li Bing-yu, and Wang Xiao-dong. Synchronous removal of high-frequency noise and breathing baseline in pulse wave signal based on wavelet analysis[J]. Beijing Biomedical Engineering, 2014, 33(6): 247-252.
[5] 李庆波, 韩庆阳. 人体血氧饱和度检测中消除脉搏波信号高频噪声的方法[J]. 光谱学与光谱分析, 2012, 32(9): 2523-2527.
Li Qing-bo and Han Qing-yang. The method of removing high-frequency noise in pulse wave signal in detecting oxygen saturation of human[J]. Spectroscopy and Spectral Analysis, 2012, 32(9): 2523-2527.
[6] 李庆波, 聂鑫, 张广军, 等. 分段滤波用于消除脉搏血氧检测中多种运动干扰的研究[J]. 光谱学与光谱分析, 2009, 29(11): 2992-2997.
Li Qing-bo, Nie Xin, Zhang Guang-jun, et al.. Study on resistance to motion artifact in pulse oximetry measurement using segment filter method[J]. Spectroscopy and Spectral Analysis, 2009, 29(11): 2992-2997.
[7] 王晓飞, 赵文俊. 基于动态光谱法的多波长脉搏血氧饱和度测量[J]. 光谱学与光谱分析, 2014, 34(5): 1323-1326.
Wang Xiao-fei and Zhao Wen-jun. Measurement of multiwavelenth pluse oxygen saturation based on dynamic spectroscopy[J]. Spectroscopy and Spectral Analysis, 2014, 34(5): 1323-1326.
[8] 张晓枫, 张香武, 赵春华, 等. 基于脉搏光谱分形算法的血氧测量研究[J]. 长春理工大学学报(自然科学版), 2014, 37(2): 95-97.
Zhang Xiao-feng, Zhang Xiang-wu, Zhao Chun-hua, et al.. Research on oximetry based on pulse sprectrum fractal algorithm[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2014, 37(2): 95-97.
[9] 凌振宝, 张铭, 熊文激, 等. 基于脉搏波传导时间的无袖带血压测量仪设计[J]. 电子测量与仪器学报, 2012, 26(12): 1080-1085.
Ling Zhen-bao, Zhang Ming, Xiong Wen-ji, et al.. Design of sleeveless blood pressure measuring instrument based on pulse wave transit time[J]. Journal of Electronic Measurement and Instrument, 2012, 26(12): 1080-1085.
[10] 王玉静, 康守强, 张云, 等. 基于集合经验模态分解敏感固有模态函数选择算法的滚动轴承识别方法[J]. 电子与信息学报, 2014, 36(3): 595-600.
Wang Yu-jing, Kang Shou-qiang, Zhang Yun, et al.. Condition recognition method of rolling bearing based on ensemble empirical mode decomposition sensitive intrinsic mode function selection algorithm[J]. Journal of Electronics & Information Technology, 2014, 36(3): 595-600.
[11] 何星, 王宏力, 姜伟, 等. 改进的自适应EEMD方法及其应用[J]. 系统仿真学报, 2014, 26(4): 869-873.
He Xing, Wang Hong-li, Jiang Wei, et al.. Improved adaptive EEMD method and its application[J]. Journal of System Simulation, 2014, 26(4): 869-873.
[12] 王姣, 李振春, 王德营. 基于CEEMD的地震数据小波阈值去噪方法研究[J]. 石油物探, 2014, 53(2): 164-172.
Wang Jiao, Li Zhen-chun, and Wang De-ying. A method for wavelet threshold denoising of seismic data based on CEEMD[J]. Geophysical Prospecting for Petroleum, 2014, 53(2): 164-172.
[13] 冯辅周, 饶国强, 司爱威, 等. 排列熵算法研究及其在振动信号突变检测中的应用[J]. 振动工程学报, 2012, 25(2): 221-224.
Feng Fu-zhou, Rao Guo-qiang, Si Ai-wei, et al .. Research and application of the arthimetic if PE in testing the sudden change of vibration signal[J]. Journal of Vibration Engineering, 2012, 25(2): 221-224.
[14] 冯辅周, 司爱威, 饶国强, 等. 基于小波相关排列熵的轴承早期故障诊断技术[J]. 机械工程学报, 2012, 48(13): 73-79.
Feng Fu-zhou, Si Ai-wei, Rao Guo-qiang, et al.. Early fault diagnosis technology for bearing based on wavelet correlation permutation entropy[J]. Journal of Machinery Engineering, 2012, 48(13): 73-79.
[15] 郑德近, 程军圣, 杨宇. 改进的EEMD算法及其应用研究[J].振动与冲击, 2013, 32(21): 22-46.
Zhen De-jin, Cheng Jun-sheng, and Yang Yu. Modified EEMD algorithm and its applications[J]. Journal of Vibration and Shock, 2013, 32(21): 22-46.
韩庆阳: 男,1988年生,研究实习员,研究方向为光电信号检测及处理.
王晓东: 男,1970年生,研究员,研究方向为光电探测及检测.
李丙玉: 男,1980年生,助理研究员,研究方向为光电探测及检测.
周鹏骥: 男,1985年生,研究实习员,研究方向为光电探测及检测.
Using EEMD to Eliminate High Frequency Noise and Baseline Drift in Pluse Blood-oximetry Measurement Simultaneously
Han Qing-yang Wang Xiao-dong Li Bing-yu Zhou Peng-ji
(Photoelectric Technology Research and Development Center, Changchun Optical Precision Machinery and Physics Institute, Chinese Academy of Sciences, Changchun 130033, China)
The measurement of blood-oxygen saturation is based on the pulse wave signal, but there are many factors impact the accuracy of measurement, such as high frequency noise caused by instrument thermal noise and baseline drift caused by the breath. A method which combines Ensemble Empirical Mode Decomposition (EEMD) and Permutation Entropy (PE) is proposed, it can decrease high frequency noise and baseline drift. The pulse wave signal is decomposed by EEMD, the PE of each Intrinsic Mode Function (IMF) is calculated and the threshold value of PE is chosen. Then the IMFs which present high frequency noise and baseline drift are judged and decreased. Finally, the signal without high frequency noise and baseline drift is achieved. A self-developed measurement device is used to obtain the pulse wave for testing validation, and the signal spectrum and AC-DC modulation ratio value are adopted to evaluate the effect. The result shows that this method could effectively remove high frequency noise and baseline drift, which is conducive to improve the accuracy of blood-oxygen saturation.
Pulse wave signal; Oxygen saturation; High frequency noise; Baseline drift; Ensemble Empirical Mode Decomposition (EEMD); Permutation Entropy (PE)
R318.04
: A
:1009-5896(2015)06-1384-05
10.11999/JEIT141390
2014-10-31收到,2015-02-06改回
*通信作者:韩庆阳 lanbohesky@126.com
