非静水压力下圆形隧洞围岩塑性区分析

张承客，李 宁,2，胡海霞

(1 西安理工大学 岩土工程研究所，陕西 西安 710048；2 中国科学院寒区旱区环境与工程研究所冻土工程国家重点实验室，甘肃 兰州 730000；3 湖南省湘电锅炉压力容器检验中心有限公司，湖南 长沙 410007)

非静水压力下圆形隧洞围岩塑性区分析

张承客1，李 宁1,2，胡海霞3

(1 西安理工大学 岩土工程研究所，陕西 西安 710048；2 中国科学院寒区旱区环境与工程研究所冻土工程国家重点实验室，甘肃 兰州 730000；3 湖南省湘电锅炉压力容器检验中心有限公司，湖南 长沙 410007)

【目的】 针对地下圆形洞室承受非静水初始压力作用下的平面应变问题，分析围岩的塑性区范围，为评价围岩稳定性和洞室支护结构的设计提供依据。【方法】 对洞室围岩弹塑性边界两侧分别采用复变函数理论和滑移线场理论得出弹性区和塑性区应力组合表达式，根据弹塑性边界上应力相等得到边界方程；通过有限元算例将本研究方法的结果与卡斯特纳等方法的分析结果进行比较，并分析静水压力的变化情况。【结果】 弹塑性边界为近似椭圆形，长轴与最大初始应力方向垂直；本研究方法与有限元分析结果更为接近，能够很好地反映洞室围岩塑性区范围；在静水压力下的分析结果与卡斯特纳公式所得塑性区半径一致。【结论】 在非静水压力下塑性区全部包围洞室时，本研究方法能够更好地用于指导支护结构设计以及围岩稳定性评价。

地下洞室；围岩；塑性区边界；非静水压力；复变函数理论；滑移线场理论

地下洞室开挖扰动原岩的初始应力状态，洞室围岩应力会进行调整达到新的平衡状态并出现应力集中，当应力状态超过屈服极限就会在洞室周围形成塑性区。因地下洞室围岩塑性区的范围是评价围岩稳定性的重要依据和洞室支护结构定量设计的理论基础，故塑性区区域界限的确定一直是人们关心的问题。

对于地下圆形洞室，人们常用卡斯特纳公式或Salençon解答等来确定其塑性区范围及洞周应力、变形状态。但在实际工程中，地下洞室初始应力场并非静水压力场，即其侧压力系数为不等于1的非轴对称应力场，此时的洞室塑性区边界不再是理想的圆形，确定其边界也就显得比较困难。

国内外研究学者针对非静水压力场下圆形洞室(圆孔)塑性区范围的研究已开展了大量工作，如萨文[1]针对无限平面中的圆孔问题，得到塑性区边界方程及弹塑性解，但结果只适用于Tresca材料。Detournay等[2-3]将萨文解扩展至符合摩尔-库伦屈服准则的材料中。卡斯特奈[4]、Carranza-Torres等[5]、张鹏等[6]、于学馥等[7]将弹性区应力公式(基尔希解答)带入塑性条件来判断围岩是否进入塑性状态，得到边界的隐式近似解。Bello-Maldonado[8]、严克强[9]、魏符[10]、孙广忠[11]、陈立伟等[12]、蔡晓鸿等[13]参考已有弹性解和轴对称条件下的塑性解，构建应力分量表达式并得出弹塑性边界解。Jiang等[14]给出了塑性区和松动区半径公式并划分了4种不同的洞室塑性破坏模式。Imamutdinov等[15]、Tokar[16]通过若干假设及前人未考虑到的因素得出解析解或半解析解。鲁宾涅依特[17]、蔡美峰[18]、陈启美[19]、魏悦广[20]采用小参数法对二向不等压作用下的圆形洞室进行研究，得到围岩弹塑性应力以及弹塑性边界线方程。

剖析前人的研究成果，可以发现其中存在以下不足：弹性区应力解具有基尔希解形式，这是缺乏理论根据的，而且究竟会产生多大的误差尚不清楚[20]；现在得到的塑性区范围较按弹塑性有限元法算得的塑性区范围小10%～30%[21]；塑性区力学模型被视为轴对称平面问题；应力平衡条件仅考虑径向应力或者切向应力导致弹塑性边界两侧区域应力分量不对等；鲜有研究者对自己研究结果的适用范围进行讨论。

本研究尝试对洞周弹性区采用复变函数法得到弹性区应力组合，按塑性区符合摩尔-库伦屈服准则并采用滑移线理论来求解其应力组合分布。根据弹塑性区边界上应力相等条件(弹塑性区域均存在3个应力分量)得到塑性区边界方程表达式，通过算例以有限元数值计算为基准比较本研究方法与前人方法的差异，并对求解方法的适用范围进行讨论，以期为不同初始应力状态下所对应的塑性区形态研究提供参考。

1 弹性基本方程

弹性力学平面问题的应力解法最终归结为在给定应力边界条件下一个双调和方程的求解问题。满足双调和方程的应力函数可以采用复数解析函数来表示双调和方程的通解。在弹塑性边界以外区域中，可以用2个正则函数η和υ表示应力分量组合表达式[22]：

(1)

(2)

式中：σx、σy、τxy为平面问题中某一点应力状态的3个应力分量；z为复变量，z=x+yi，其中x，y分别为z的实部和虚部，i为虚数单位。

考虑作用于洞室内壁和无穷远处的应力条件，得到η和υ的表达式为：

(3)

(4)

2 塑性基本方程

塑性区存在于洞周与弹性区之间，满足摩尔-库伦塑性准则。塑性区平面应变问题的平衡方程为：

(5)

式中：γ为岩土体的容重，β为重力方向和y轴的夹角。当不考虑岩土体自重时，等式右端为0，以下分析均不考虑岩土体自重。

摩尔库伦屈服条件的表达式为：

(6)

式中：c为岩体黏聚力，φ为岩体内摩擦角。

式(5)、(6)是滑移线场理论的应力基本方程，直接求解这2个方程存在困难，但可以应用特征线法来求解。

x-y坐标系中任一满足屈服条件的点的平面应力分量可表示为：

(7)

式中：σ指平均应力(即应力圆圆心应力值)，σ=(σx+σy)/2=(σ1+σ3)/2,σ1为大主应力，σ3为小主应力；R为应力圆半径，在摩尔-库伦屈服准则条件下，R=σsinφ+c·cosφ或R=(σ1-σ3)/2；θ为第一主应力σ1方向与x轴的夹角。经过相关推导[23]，能够得到σ与θ沿滑移线的变化方程为：

(8)

式中：Cα和Cβ为常量，沿着不同的滑移线，常量Cα和Cβ的数值一般是不同的。

在塑性区内，塑性滑移发生在与最大主应力成45°-φ/2角度的方向上，对于圆形地下洞室，洞周塑性区滑移线方程在极坐标系r-ψ中具体方程表示为r=R0e±ψ·tan (45°-φ/2)(式中，R0为圆形洞室半径，ψ=θ-π/2)，即塑性区内滑移线形式为对数螺线。

采用两族表示洞周塑性区内的滑移线场方程为：

(9)

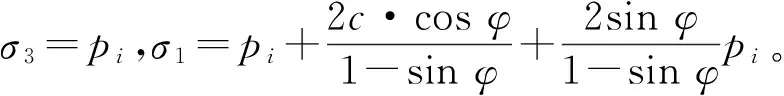
图1 洞周塑性应力状态的Mohr圆Fig.1 Mohr circle of tunnel periphery plastic stress state

通过在α滑移线上考虑2点A和B(其中A点位于洞室内壁，B点位于塑性区内)来建立塑性区内任一点的平均应力表达式。将A和B点条件带入式(8)和(9)中的第1式能够得到如下2个表达式：

ln(σA+c·cotφ)-2θAtanφ=ln (σB+c·cotφ)-2θBtanφ。

(10)

(11)

式中：σA、σB为A点和B点处的平均应力，θA、θB为A点和B点处第一主应力与x轴的夹角，rB为B点在极坐标系r-ψ下的极径，ψA、ψB为A点和B点的极角。

同时，根据ψB-ψA=θB-θA，结合边界条件能够得到整个塑性区内平均应力σ的表达式为：

(12)

同时，根据R=σsinφ+c·cosφ，可得：

(13)

将上面2式带入式(7)，则可以得到塑性区内应力组合表达式为：

(14)

(15)

3 边界方程求解

式(1)和(2)在弹性区以及弹塑性边界上成立。可以考虑将方程式等号左边应力通过塑性区内考虑洞室内壁边界条件的特征线法得出，而函数η和υ是针对弹性区域，从此方面来讲，方程式就只是在弹塑性边界上成立。

引入保角映射函数z=ω(ζ)，将弹塑性边界的外部映射为复平面ζ上单位圆的内部，其具有如下的幂级数形式：

(16)

式中：ζ为复平面上任一点，用极坐标表示为ζ=ρeiθ=ρ(cosθ+isinθ)，其中ρ和θ为ζ点的极坐标，在单位圆边界上时ζ=σ=eiθ，即ρ=1;s、s0、s1、s2、s3…为函数待定系数。

同时，令η(z)=η(ζ)，υ(z)=υ(ζ)，且具有如下的形式：

η(ζ)=a0+a1ζ+a2ζ2+a3ζ3+…。

(17)

υ(ζ)=b0+b1ζ+b2ζ2+b3ζ3+…。

(18)

式中：a0、a1、a2、a3…及b0、b1、b2、b3…为函数待定系数。

将式(1)等号左边部分在弹塑性边界上展开成傅立叶级数表达形式，即：

(19)

式中：dn为各阶级数的待定系数，σn表示以σ为复变量表示的幂级数中的n次方项，n为整数。

从式(1)、(17)及(19)，可得在弹塑性边界上有：

dn=2an,n≥1。

(20)

同时，根据无穷远处边界条件可得：

(21)

式中：Re(a0)表示系数a0的实部。

同理，将式(2)等号左边部分展开成傅立叶级数表达形式：

(22)

(23)

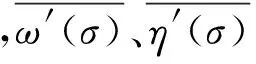
对上式应用柯西积分公式进行积分，对于|ζ|<1的单位圆内区域，有如下的等式成立：

(24)

(25)

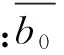
考虑无穷远处只有水平向和竖直向均布应力，无剪应力，则式(25)中t=0。同时令：

(26)

式中：hn为各阶级数的待定系数。

对上式进行柯西积分后得：

(27)

据式(24)、(25)、(26)可以得到如下的系数关系：

gn=2hn,n≥1。

(28)

g0=2h0+(1-λ)p。

(29)

对式(26)进行展开，根据等式两边不同σ次项前的系数相等能够得出映射函数ω(ζ)、η(ζ)待定系数和hn之间的关系为：

(30)

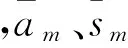
根据式(28)、(29)可得k>0，且上式中n取值应为映射函数的最高项。

因本研究的对象是圆形洞室，坐标系原点位于洞室圆心处，其塑性区边界是中心对称的，所以映射函数ω(ζ)中s0、s2、s4…系数就不存在，同时映射函数的系数均为实数。

考虑到计算量以及精确程度，本研究映射函数取到ζ的5次方，即：

(31)

4 计算实例

计算模型为半径R0=3.0 m的深埋圆形洞室，忽略开挖过程对围岩的扰动，洞室不考虑任何支护情况，洞室埋深为200 m，考虑四级围岩，围岩的物理力学参数取弹性模量E=3 GPa，泊松比μ=0.32，黏聚力c=0.8 MPa，内摩擦角φ=30°，容重γ=25 kN/m3，侧压力系数λ=0.8。

有限元模型分析区域取距洞周6倍洞径范围，洞室不考虑任何支护情况。模型底部为竖直向约束，左右边界为水平向约束，顶部不施加约束。岩土体材料采用各向同性、理想弹-塑性本构模型以及Mohr-Coulomb强度准则。

根据前文推导的弹塑性边界方程求解方法以及卡斯特纳方法[4]、郑颖人修正方法[7]，得到几种不同方法下洞周塑性区边界，以数值仿真分析系统FINAL[24]的有限元数值方法为基准进行比较分析。最后将本研究方法应用于静水压力情况中(即侧压力系数为1时)并与卡斯特纳公式得到的塑性区半径进行对比。

(32)

σy-σx-2iτxy=Cz2。

(33)

(34)

根据式(20)的系数关系，可得：

(35)

式中：d2、d4为待定系数。再根据边界条件式(21)可得：

(36)

同时，在弹塑性边界上有：

(37)

据式(28)、(29)，得：

(38)

式中：h0、h2、h4、h6、h8、h10和g0、g2、g4、g6、g8、g10均为待定系数。最后根据式(30)能够得到如下方程组：

(39)

将式(35)和式(38)代入(39)式，根据式(39)以及边界条件式(36)得到四元二次方程组，通过迭代求解,可以求出弹塑性边界方程式(31)中的待定系数s=4.355 8，s1=0.375 6，s3=-0.016 4，s5=0.001 4。图2绘出了本研究映射函数方程、卡斯特纳方法[4]和郑颖人修正方法[7]表示的弹塑性边界以及有限元数值计算得到的塑性区分布情况。

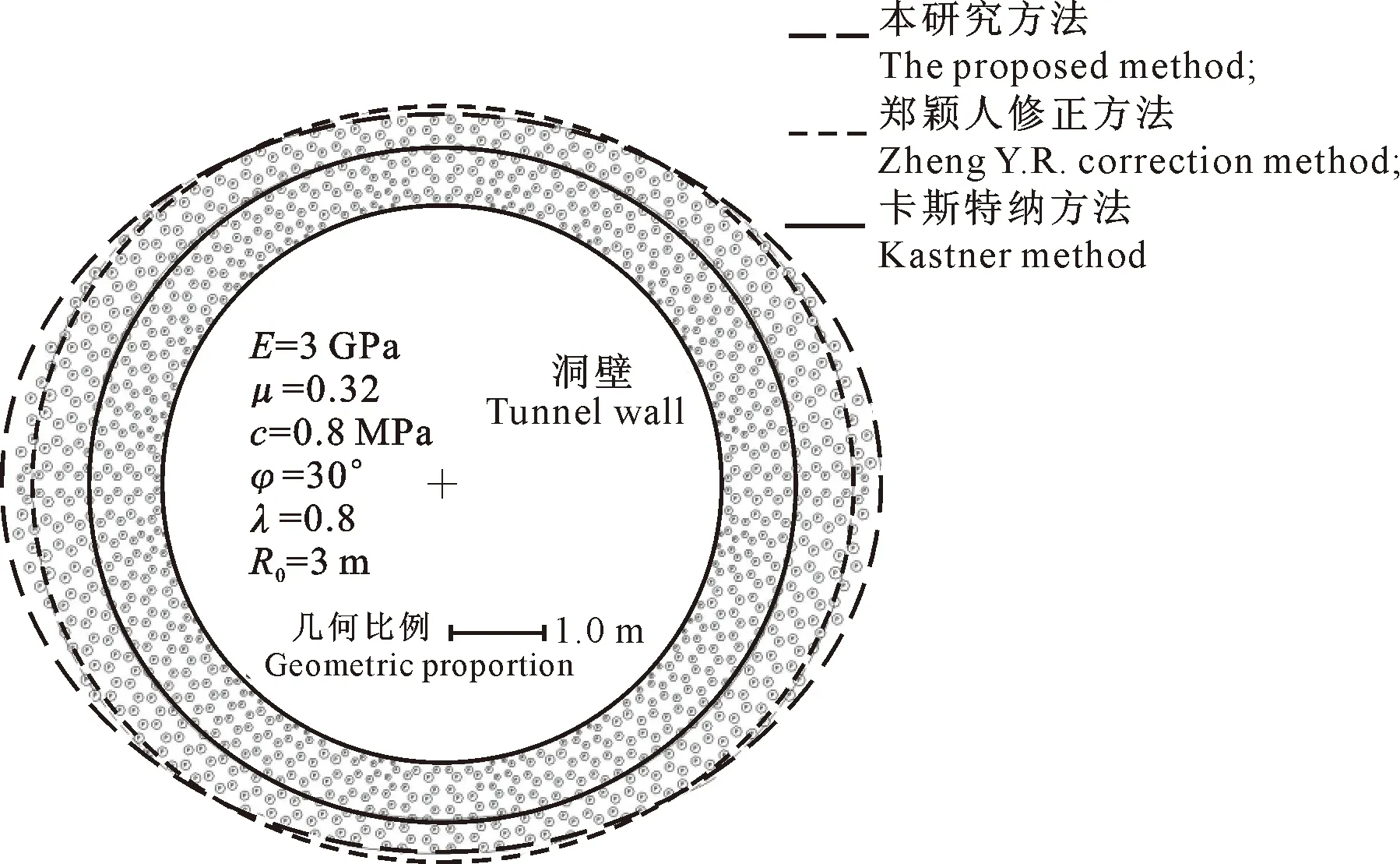
图2 不同方法的弹塑性边界与数值计算的塑性区分布Fig.2 Elastoplastic interfaces of different methods and distribution of plastic zone

从图2可以看出，本研究方法得到的弹塑性边界为近似椭圆形，长轴位于水平边墙部位，与最大初始应力方向垂直；卡斯特纳方法因未考虑塑性应力重分布，其塑性区边界线较有限元塑性分布范围小且近乎圆形，在边墙中部塑性区深度较有限元数值计算方法计算结果小20%；郑颖人修正方法是对卡斯特纳方法的修正，其塑性区边界有所增大，但在边墙部位的塑性深度依然较有限元数值计算方法计算结果小近10%。通过比较可以发现，本研究方法能够更好地反映圆形洞室在非轴对称应力条件下塑性区全部包围洞室情况时的洞周塑性区范围。当考虑静水压力，即侧压力系数λ=1时，弹塑性边界为圆形，边界映射函数方程中s1=s3=s5=0，从式(36)可以得到围岩塑性区半径为：

该结果与卡斯特纳公式的计算结果一致。

5 适用范围分析

塑性区内任一单元体必须由完全在塑性区域内的2条应力滑移线与区域边界相连，即每条应力滑移线与区域边界相交不多于1次，只有满足这一条件，弹塑性边界才是静定的，否则即使所有的边界条件都只与应力有关，弹塑性边界仍然不一定是静定的[25]。静定条件的极限情况就是应力滑移线与弹塑性边界相切。由此可知，本研究提出的方法适用于塑性区全部包围洞室(不包括局部包围以及蝴蝶状塑性区)的情况。

前人对萨文解[1-3]和Detournay解[2-3]适用范围的研究均是基于静定条件和弹塑性边界短轴大于洞室半径2个条件进行的，其中静定条件包括塑性区全部包围洞室和局部包围洞室2种情况。边界短轴大于洞室半径条件应用于摩尔-库伦材料时，无法得到显式的弹塑边界方程表达式，在Detournay等[3]的研究中，边界方程是一个高斯超几何方程，这从上文中的映射函数也可以得到反映，故无法与静定条件综合明确得出其严格的适用范围。Carranza-Torres等[5]根据Detournay等[3]的研究结果得到侧压力系数极限值klim，当侧压力系数小于该值时，解是静定的，但依旧包括塑性区局部包围洞周的情况。

本研究先根据Detournay等[26]的静定条件推导出在不同竖向初始应力下侧压力系数的适用范围(考虑λ≤1的情况)，当然此范围包括塑性区全部或局部包围圆形洞室2种情况，然后再结合圆形洞室基尔希弹性公式对塑性区形态进行区分，其中洞室不考虑任何支护情况。

当侧压力系数λ≤1时，根据静定条件得出最小的适用侧压力系数为：

(40)

同时，对于λ<1，塑性区首先出现于水平边墙部位，故要想塑性区全部包围洞周就需要判断在初始应力场下，顶拱部位是否达到屈服极限，在此就以顶拱部位须达到塑性屈服极限来对初始应力场下的侧压力系数进行约束，得到的侧压力系数范围为：

(41)

式中：σci为围岩单轴抗压强度，σci=2ccosφ/(1-sinφ)。 结合(40)和(41)式以及其他边界条件，得到在内摩擦角φ=30°时洞室在不同初始应力场状态下所对应的不同围岩破坏模式(即塑性区形态)如图3所示。其他内摩擦角下的塑性区形态可同理求得。

图3 未支护情况不同初始应力场状态与围岩破坏模式的关系(φ=30°)Fig.3 Relationship between the initial stress and failure modes of unsupported tunnel (φ=30°)

从图3可以看出，本研究弹塑性边界方程分析方法适用于区域③。图中区域①对应的是纯弹性状态，其中在侧压力系数<1/3时，顶拱部位将出现拉应力，侧压力系数>1/3时围岩无拉应力分布。区域②对应的是围岩塑性区局部包围洞室，区域④对应的是蝴蝶状塑性区形态。式(41)为区域②与③的分界线方程；式(40)为区域④与区域②+③的分界线方程。m*=1曲线下方区域对应的是初始应力作用下围岩已经全部屈服的情况，显然这在工程中非常少见。根据图3便可以快速方便地针对不同的初始应力状态判断无支护情况下，洞室全部开挖完成后围岩的塑性区形态，可以方便地指导支护结构设计及围岩稳定性判断。

6 结 论

本研究针对工程实际中，地下洞室多处于非静水压力荷载条件下的现状，对其塑性区边界求解问题进行研究，得到的主要结论如下：

(1) 采用复变函数得到洞室围岩弹性区应力组合表达式，塑性区符合摩尔-库伦屈服准则，并可采用滑移线理论求解得到应力组合分布。

(2) 根据弹塑性区边界应力相等条件，得到塑性区边界方程映射函数表达式，以有限元数值结果为基准比较发现，本研究方法比卡斯特纳方法和郑颖人修正方法能更好地反映非静水压力下洞周围岩塑性区范围。同时，在侧压力系数等于1的静水压力下，本研究方法分析结果与卡斯特纳公式所得塑性区半径一致。

(3) 根据解的静定条件和基尔希弹性公式对本研究方法适用的侧压力系数范围进行了讨论，得出了方法的适用范围以及洞室未支护情况下不同初始应力场状态所对应的围岩塑性区形态。

[1] 萨文 г н．孔附近的应力集中 [M].卢鼎霍，译．北京：科学出版社，1958：200-206． Savin G N．Stress concentration around holes [M].Lu D H， translated．Beijing：Science Press，1958：200-206．(in Chinese)

[2] Detournay E．Two-dimensional elastoplastic analysis of a deep cylindrical tunnel under non-hydrostatic loading [D].Minnesota：University of Minnesota，1983．

[3] Detournay E，Fairhurst C．Two-dimensional elastoplastic analysis of a long,cylindrical cavity under non-hydrostatic loading [J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts，1987，24(4)：197-211．

[4] 卡斯特奈 H．隧道与坑道静力学 [M].上海：上海科学技术出版社，1980：56-61． Kastner H．Tunnel and trench statics [M].Shanghai：Shanghai Scientific and Technical Publishers，1980：56-61．(in Chinese)

[5] Carranza-Torres C，Fairhurst C．Application of the convergence-confinement method of tunnel design to rock masses that satisfy the Hoek-Brown failure criterion [J].Tunnelling and Underground Space Technology，2000，15(3)：187-213．

[6] 张 鹏，李 宁，何 敏．软岩圆形隧洞衬砌支护时机现场变形监测判据研究 [J].西安理工大学学报，2007，23(2)：140-143． Zhang P，Li N，He M．Theoretical estimation of the supporting time in soft rocks tunnels under high initial stress [J].Journal of Xi’an University of Technology，2007，23(2)：140-143．(in Chinese)

[7] 于学馥，郑颖人，刘怀恒，等．地下工程围岩稳定分析 [M].北京：煤炭工业出版社，1983：156-169． Yu X F，Zheng Y R，Liu H H，et al．Underground engineering rock stability analysis [M].Beijing：China Coal Industry Publishing House，1983：156-169．(in Chinese)

[8] Bello-Maldonado A A．General elasto-plastic theory applied to circular tunnels(K0≠1) [C]//Elsworth D，Tunucci J P，Heasley K A．Rock Mechanics in the National Interest．Washington D C：American Rock Mechanics Association，2001：1119-1126．

[9] 严克强．不对称荷载作用下圆洞围岩塑性区的估算方法 [J].岩土工程学报，1980，2(2)：74-79． Yan K Q．Estimation method of surrounding rock mass plastic zone of round tunnel under asymmetric load [J].Chinese Journal of Geotechnical Engineering，1980，2(2)：74-79．(in Chinese)

[10] 魏 符．对“不对称荷载作用下圆洞围岩塑性区的估算方法”的讨论意见 [J].岩土工程学报，1982，4(1)：116-118． Wei F．Discussion on “Estimation method of surrounding rock mass plastic zone of round tunnel under asymmetric load” [J].Chinese Journal of Geotechnical Engineering，1982，4(1)：116-118．(in Chinese)

[11] 孙广忠．岩体力学基础 [M].北京：科学出版社，1983：160-162． Sun G Z．Fundamental of rock mass mechanics [M].Beijing：Science Press，1983：160-162．(in Chinese)

[12] 陈立伟，彭建兵，范 文，等．基于统一强度理论的非均匀应力场圆形巷道围岩塑性区分析 [J].煤炭学报，2007，32(1)：20-23． Chen L W，Peng J B，Fan W，et al．Analysis of surrounding rock mass plastic zone of round tunnel under non-uniform stress field based on the unified strength theory [J].Journal of China Coal Society，2007，32(1)：20-23．(in Chinese)

[13] 蔡晓鸿，蔡勇平．水工压力隧洞结构应力计算 [M].北京：中国水利水电出版社，2004：74-76． Cai X H，Cai Y P．Structural stress calculation for hydraulic pressure tunnel [M].Beijing：China Water & Power Press，2004：74-76．(in Chinese)

[14] Jiang Y，Yoneda H，Tanabashi Y．Theoretical eastimation of loosening pressure on tunnels in soft rock [J].Tunnelling and Underground Space Technology，2001，16(2)：99-105．

[15] Imamutdinov D I，Chanyshev A I．Elastoplastic problem of an extended cylindrical working [J].Journal of Mining Science，1988，24(3)：199-207．

[16] Tokar G．Generalization of Galin’s problem to frictional materials and discontinuous stress fields [J].International Journal of Solids and Structures，1990，26(2)：129-147．

[17] 鲁宾涅依特 K B．矿山岩石力学的几个问题 [M].马英方，译．北京：煤炭工业出版社，1960：155-162． Ruppneyt K B．Several problems in mining rock mechanics [M].Ma Y F，translated．Beijng：China Coal Industry Publishing House，1960：155-162．(in Chinese)

[18] 蔡美峰．岩石力学与工程 [M].北京：科学出版社，2002：323-326． Cai M F．Rock mechanics and engineering [M].Beijing：Science Press，2002：323-326．(in Chinese)

[19] 陈启美．坑道围岩弹塑性应力的小参数解法 [J].煤炭学报，1964，1(4)：61-67． Chen Q M．Method of distribution applying to the elasto-plastic stress analysis of mine entries [J].Journal of China Coal Society，1964，1(4)：61-67．(in Chinese)

[20] 魏悦广．两向不等压作用下圆形巷道弹塑性分析摄动解 [J].岩土工程学报，1990，12(4)：11-20． Wei Y G．Perturbation solutions for elasto-plastic analysis of circular tunnel under unequal compression in two directions [J].Chinese Journal of Geotechnical Engineering，1990，12(4)：11-20．(in Chinese)

[21] 夏永旭，王永东．隧道结构力学计算 [M].北京：人民交通出版社，2004：167-175． Xia Y X，Wang Y D．Mechanical calculations of the tunnel structure [M].Beijing：China Communications Press，2004：167-175．(in Chinese)

[22] 陈子萌．围岩力学分析中的解析方法 [M].北京：煤炭工业出版社，1994：1-20． Chen Z M．Analytic method of mechanical analysis for the surrounding rock [M].Beijing：China Coal Industry Publishing House，1994：1-20．(in Chinese)

[23] 龚晓南．土塑性力学 [M].2版．杭州：浙江大学出版社，1997：272-281． Gong X N．Soil plastic mechanics [M].2ndEdition．Hangzhou：Zhejiang University Press，1997：272-281．(in Chinese)

[24] Swoboda G．Program system final-finite element analysis program for linear and nonlinear structure [R].Innsbruck：University of Innsbruck，1998．

[25] Hill R．The mathematical theory of plasticity [M].Oxoford：Clarendon Press，1950：242-245．

[26] Detournay E，John C M S．Design charts for a deep circular tunnel under non-uniform loading [J].Rock Mechanics and Rock Engineering，1988，21(2)：119-137．

Analysis of elastoplastic interface of circle tunnel under non-hydrostatic loading

ZHANG Cheng-ke1，LI Ning1,2，HU Hai-xia3

(1InstituteofGeotechnicalEngineering，Xi’anUniversityofTechnology，Xi’an，Shaanxi710048，China；2StateKeyLaboratoryofFrozenSoilEngineering，ColdandAridRegionEnvironmentalandEngineeringResearchInstitute，ChineseAcademyofSciences，Lanzhou，Gansu730000，China；3HunanXiangdianBoiler&PressureVesselTestCenterLtd.，Changsha，Hunan410007，China)

【Objective】 This study analysed the plastic zone of surrounding rock to overcome the plane strain problem of elastoplastic interface of underground circle tunnel subject to non-hydrostatic initial stress and to provide basis for evaluating surrounding rock stability and designing supporting structure.【Method】 In elastic and plastic regions,the combined stress expressions were derived using complex function theory and slip line field theory,respectively.According to continuous stress condition in elastoplastic boundary,the interface equation was determined.Using FEM numerical result as benchmark,the result of proposed method was compared with methods including Kastner method and the change of hydrostatic loading was analyzed.【Result】 The elastoplastic boundary was approximately elliptical,with long axis perpendicular to the maximum initial stress.The proposed method was similar to FEM analysis and the results well showed the plastic zone of surrounding rock.The radius of plastic zone under hydrostatic loading was consistent with Kastner method.【Conclusion】 When the circular tunnel was completed covered under non-hydrostatic loading,the proposed method could be used to guide the design of supporting structure and evaluation of surrounding rock stability.

tunnel；surrounding rock；plastic zone boundary；non-hydrostatic loading；complex function theory；slip line field theory

2014-05-07

国家自然科学基金项目“高温环境下水工引水隧洞围岩与支护衬砌结构受力特点研究”(51179153)

张承客(1984-)，男，福建福鼎人，在读博士，主要从事地下工程及岩体动力学特性研究。E-mail:zck927@126.com

李 宁(1959-)，男，陕西耀县人，教授，博士，博士生导师，主要从事地下洞室、边坡稳定性分析以及岩体动力学研究。E-mail:ningli@xaut.edu.cn

时间:2015-03-12 14:17

10.13207/j.cnki.jnwafu.2015.04.022

TV672.1

A

1671-9387(2015)04-0215-08

网络出版地址:http://www.cnki.net/kcms/detail/61.1390.S.20150312.1417.022.html