考虑负荷时间弹性的分行业峰谷电价研究
2015-07-11李龙
李龙
(国网湖南省电力公司,湖南 长沙410007)
电力是现代社会发展的重要支撑和现代生活正常运转的命脉,近年来国内电力供需矛盾时常发生,需求时间不均衡现象严重,造成单位发电成本上升、电网调峰困难、供电可靠性降低及高峰时段限电拉闸等一系列问题。在此背景下,峰谷分时电价〔1〕作为市场经济体制下的一种经济运行调控手段受到全社会的重视,对于促进电力工业与经济、环境、社会协调发展,发挥着重要作用。
峰谷分时电价是需求侧管理最有效的措施〔2-4〕,其基本思想是通过价格信号引导用户削峰填谷,提高电网负荷率和达到安全运行水平,减少或推迟安装新设备的目的。峰谷电价是否合理,是实现有效削峰填谷的关键。峰谷电价差太小,用户响应不足,达不到应有的削峰填谷效果;峰谷电价差太大,用户过响应,对供电方造成较大的利益损失,甚至会造成峰谷倒置的现象。同时,不同行业在用电时间上的选择余地不同,即负荷时间弹性大小不一样,其对峰谷电价的响应也不同。为了更科学地制定峰谷分时电价,提高电力系统的安全性、经济性,需要深入研究不同行业的负荷特性。
目前,已有大量文献对峰谷电价定价方案进行了研究。文献〔5-6〕从发电侧与售电侧联动的角度研究了峰谷分时电价的设计问题。文献〔7-9〕通过分析用户需求与价格的关系,建立了基于需求弹性的峰谷分时电价模型。在考虑需求弹性的基础上,文献〔10〕以提高用户的用电满意度作为目标,把为客户服务的理念引入电力企业工作中。文献〔11〕采用基于代理的模型模拟改制的电力市场,发掘消费者的需求价格弹性对电力市场的性能的影响。这些文献从不同的角度对峰谷电价进行了研究,但定价方都没能直观把握不同行业用电在时间上选择的余地。
在此基础上,文中给出了负荷时间弹性大小的计算方法,建立了基于负荷时间弹性的分行业峰谷分时电价调整模型。利用该模型对现有峰谷电价进行调整,在保证电力公司与用户利益的情况下,能有效地提高系统的负荷率。
1 负荷时间弹性的量化
负荷时间弹性,指的是负荷在时间上的选择余地。负荷时间弹性影响因素众多,行业差别明显,即使是同一个用户,在不同的时期其负荷时间弹性也是不同的。针对不同的应用,其考虑的影响因素不同。文中研究负荷时间弹性在分行业峰谷电价中的应用,是为了更加有效的移峰填谷,改善系统的负荷曲线,提高系统的负荷率。考虑的影响因素包括日负荷曲线的相似程度和波动情况、单位电量生产的产品价值、用户高峰负荷与系统高峰负荷的重叠程度。以下分别对各影响因素进行量化。
1.1 日负荷曲线相似度
用户每天的日负荷曲线越相似,说明用户的负荷在时间上的分配相对固定,用电有比较稳定的规律,用电负荷在时间上的选择余地较小,一定程度上表明时间弹性小。用户日负荷曲线的相似度用σir表示。
1)取该类电力用户定价前30 天的日负荷曲线,取日平均负荷平均值作为该天负荷的基值,将每一时段(24 小时)的负荷标幺化,得到第u日t时段的负荷Piut:

其中:
i 代表第几类客户,i=1,2,3,4,5…;
u 代表一月中的30 天,u=1,2,…,30;
t 代表一天的24 小时,T=1,2…,24;
Liut为i 行业第u 天t 时的电力负荷;
Liut为i 行业第u 天的日平均负荷;
2)将30 天每天对应时段的负荷值进行均方差计算,得到一天24 时段的负荷均方差值σit:
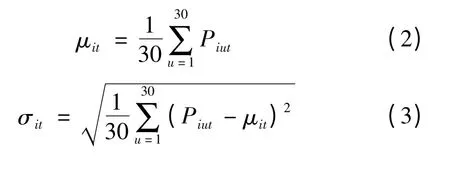
3)将σit进行均方差计算,得到σir:

1.2 日负荷曲线波动
在现有峰谷电价下,用户的日负荷曲线波动越小,用户的负荷率高,说明用户已较为充分利用其负荷能力,用户负荷选择的余地小,一定程度上表明时间弹性小。
1)计算每天的时负荷均方差δiu,即日负荷曲线(以小时为单位)的波动情况
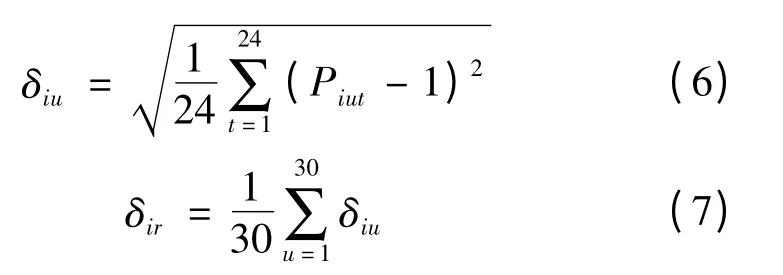
行业的用电量不是保持绝对不变的,所以行业用电量在很小范围内的波动不能认为该行业具有负荷时间弹性,为此,设定一个门槛值,
当σir≤σir时,σi=0;当σir>σir时,σi=σir;
当δir≤δir时,δi=0;当δir>δir时,δi=δir。
1.3 单位电量生产的产品价值
对于不同行业,单位电量的产品价值是不同的,用αi表示。对于电费成本较高的行业,利用低电价可以较大程度上降低其生产成本,其移峰填谷的积极性较高,一定程度表明其负荷时间弹性大。
1.4 用户负荷与系统高峰重量度
用户的负荷时间弹性,可以反映为在一定时间段内,用户原计划在该时间段内使用的电量,可转移到其他时段的比例。文中从实际需求出发,考虑的是从系统负荷高峰转移到系统负荷低谷的比例的潜力,用βi表示。用户负荷高峰与系统负荷高峰重叠越大的用户,其可以移动的负荷比例的潜力越大,一定程度表明其负荷时间弹性越大。
1)对于负荷波动较大的用户

其中:ki'为一月内企业负荷最高的30K 小时与系统高峰负荷时段的重合次数;K 为在进行峰谷时段划分时,每天系统负荷高峰小时数。
2)对于负荷波动较小的用户,βi取1。综上所述,负荷时间弹性可以表示为:

2 基于负荷时间弹性的峰谷电价模型
2.1 目标函数
实施峰谷分时电价的主要目标是削峰填谷,提高系统的负荷率。所以把目标函数设定为系统的日负荷率。
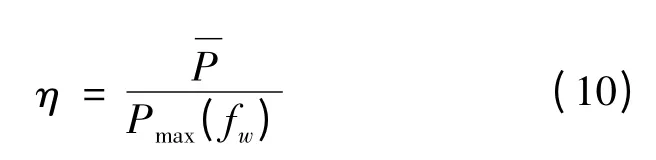
2.2 约束条件
1)为了简化模型,假设实施基于负荷时间弹性峰谷电价前后平时段的电价不变,即:
绩效不仅直接关系着个人的业绩,也深刻影响着一个单位的发展。绩效考核的目的是激发工作人员的主动性,提高其绩效水平并通过考核使员工的个人目标和单位的整体目标趋于一致。目前我国多数高校并未构建一套完善的财务绩效评价指标体系,通常把财务分析指标作为基准内容。从实际情况来看,因为该项指标主要凭借价值性指标对财务的具体结果进行评价,因此无法全面、客观反映高校的实际财务情况,难以全面反映经济考评中的非经济指标的重要性。在充分考虑高校具体情况的基础上,有必要构建一套相对完善的高校财务人员评价体系。

2)在现有峰谷电价和负荷特性情况下,fiw越大的用户,其从系统负荷高峰移动到系统负荷低谷的潜力越大,为了充分利用其移峰填谷的潜力,其峰谷电价比应越大。令系统的电价为负荷时间弹性的线性函数,则:

其中,A >0,B <0。PiTP',PiTF',PiTV'分别为i 行业实施基于负荷时间弹性的峰谷电价前峰、平、谷时的电价;PiP,PiF,PiV分别为i 行业实施基于负荷时间弹性的峰谷电价后峰、平、谷时段的电价。
3)为了保证用户和供电方的利益,供电公司在实施基于负荷时间弹性的峰谷电价后平均销售电价不能上涨,其总收益不能低于实施前的λ 倍。

其中:QiTP',QiTF',QiTV'分别为i 行业实施基于负荷时间弹性的峰谷电价前峰、平、谷时段的用电量;QiP,QiF,QiV分别为i 行业实施基于负荷时间弹性的峰谷电价后峰、平、谷时的用电量。
4)为了避免峰谷倒置,其峰谷电价比不能过大。

同时,为了控制某一行业的平均电价变化幅度,峰时段与谷时段电价变化的幅度不能相差太大。

其中:ΔPiP,ΔPiV分别为某一行业高峰和低谷时的电价调整幅度,C1,C2分别实施基于负荷时间弹性前后的峰谷电价比。
5)电力价格的变化会引起需求的变化,对于不同行业,其价格的变化引起的需求反应不同。所以,应该建立分行业的峰谷分时电价弹性矩阵,来区别不同行业的需求价格弹性〔9〕。

其中,Ei为i 行业峰谷分时电量电价弹性矩阵。
3 算例仿真
某省目前实施的是四种电价,假设尖峰电价时段与高峰电价时段对负荷时间弹性的峰谷电价有相同的响应,且在计算负荷转移量时,把尖峰时段归结为高峰时段。时段划分为高峰8:00—11:00 与15:00—2:00,平 段7:00—8:00,11:00—15:00 与22:00—23:00,低谷23:00—7:00。在算例仿真时,取5 个不同的行业,设=0.01,=0. 05,λ=0. 98,C1=3,C2=3。
图1 为系统负荷曲线,从调整前的负荷曲线可以看出,在进行峰谷时段划分时,把11:00—13:00归为平段不符合用电负荷的实际情况。系统仿真曲线表明,调整后有效地降低了高峰负荷,增加了低谷负荷。图2 为水泥行业负荷曲线,通过调整前后的负荷曲线对比表明基于负荷时间弹性的峰谷分时电价充分挖掘了该行业移峰填谷的潜力。
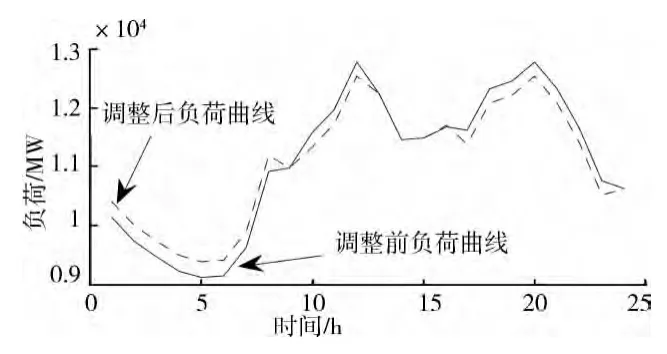
图1 系统负荷曲线

图2 水泥行业负荷曲线
调整前后各行业电价和负荷见表1,2。

表1 各行业电价

表2 各行业负荷
表1,2 表明,不同行业的负荷时间弹性差别较大。对于负荷时间弹性大的行业,应该设置较大的峰谷电价比,充分地转移高峰时期的负荷,提高系统负荷率。算例结果显示,对不同负荷时间弹性的行业设置不同的峰谷电价后,各行业的高峰总负荷为15.297 2 MW,比调整前降低了3.90%。各行业的低谷总负荷为14.502 1 MW,比调整前提高了4.45%。系统的负荷率由调整前的0.833 2 提高到了调整后的0.846 2,有效地提高了系统的负荷率。
4 结论
1)影响负荷从系统负荷高峰移动到系统负荷低谷潜力的因素是日负荷曲线的相似程度和波动情况、单位电量生产的产品价值、用户高峰负荷与系统高峰负荷的重叠程度。对于某些用户,其负荷在一个电价周期内波动很少或者其负荷高峰不在系统负荷高峰时段,则认为其负荷移峰填谷的潜力小,其峰谷电价维持原方案。
2)用户负荷从系统负荷高峰移动到系统负荷低谷的潜力反映了其负荷对系统负荷高峰产生的影响。所以,峰谷时段划分对基于负荷时间弹性的分行业峰谷分时电价调整方案的实施效果产生重要影响。合理的划分峰谷时段,才能可靠地反应各行业负荷对系统负荷高峰的影响,才能更有效地削峰填谷,达到负荷率最高的目的。
3)基于时间弹性的分行业峰谷分时电价调整能满足需求侧管理的目标,即在不损害发电侧、供电侧与用户利益的前提下,提高社会的总体效益。
〔1〕中华人民共和国国家质量监督检验检疫总局. GB/T 2900.84—2009 电工术语. 电价〔S〕. 北京:中国标准出版社,2009.
〔2〕 Boshell F,Veloza O P. Review of developed demand side management programs including different concepts and their results〔C〕//Transmission and Distribution Conference and Exposition .Bogota,Columbia:IEEE/PES,2008:1-7.
〔3〕Kirschen D S. Demand-side view of electricity markets〔J〕. IEEE Transactions on Power Systems,2003,18(2):520-527.
〔4〕Huang D,Billinton R. Effects ofload sector demand side management applications in generating capacity adequacy assessment〔J〕. IEEE Transactions on Power Systems,2012,27(1):335-343.
〔5〕谭忠富,陈广娟,赵建保,等. 考虑以节能调度为导向的发电侧与售电侧峰谷分时电价联合优化模型〔J〕. 中国电机工程学报,2009,29(1):55-62.
〔6〕胡福年,汤玉东,邹云. 考虑双边价格联动的峰谷分时电价机理研究〔J〕. 中国电机工程学报,2007,27(25):61-66.
〔7〕Celebi E,Fuller J D. A model for efficient consumer pricing schemes in electricity markets〔J〕. IEEE Transactions on Power Systems,2007,22(1):60-67.
〔8〕Yu R,Yang W,Rahardja S. Astatistical demand-price model with Its application in optimal real-time price〔J〕. IEEE Transactions on Smart Grid,2012,4(3):1 734-1 742.
〔9〕束洪春,董俊,吴水军,等. 销售侧分行业实行丰枯峰谷分时电价初探〔J〕. 电力系统自动化,2006,30(14):36-40.
〔10〕丁伟,袁家海,胡兆光. 基于用户价格响应和满意度的峰谷分时电价决策模型〔J〕. 电力系统自动化,2005,29(20):10-14.
〔11〕Thimmapuram P R,Kim J. Consumers'price elasticity of demand modeling with economic effects on electricity markets using an agent-based model〔J〕. IEEE Transactions on Smart Grid,2013,4(1):390-397.
