纯弯作用下深海夹层管复合结构屈曲失稳分析

雷明玮，龚顺风，胡 勍

（1.浙江大学 结构工程研究所，浙江 杭州310058；2.中国联合工程公司，浙江 杭州310052）

随着海洋油气资源开发由浅海向深水和超深水海域迈进，人们对海底管道提出了更高的要求.深海的低温、高压环境使传统的单层管应用受到诸多限制，无法满足管道复杂的受力和保温绝热要求.夹层管由内、外两层薄壁钢管以及填充于两管环形空间的轻质保温绝热材料构成，具有良好的层间黏结性能.夹层管不仅可以提高内管输送介质的流动保障，利于深海油气资源的长距离输送，还可以减轻管道的浮重度，并提高结构的整体受力性能，在全生命周期内降低了安装、维护和运行成本，具有显著的经济效益和广泛的应用前景.

目前，针对单层管在深海铺设及服役期间的屈曲失稳问题，国内外学者已经开展了广泛、深入的研究［1-9］，而有关夹层管复合结构的屈曲失稳研究才刚刚起步.Kardomateas等［10］采用数值解析方法，在假定材料为弹性的基础上研究了外压作用下夹层管的屈曲失稳性能.Estefen等［11］通过将小尺度比例模型实验和数值模拟相结合，研究了夹芯层分别为水泥砂浆和聚丙烯的夹层管在外压和轴向弯曲组合作用下的极限承载力，探究了夹层管应用于深海油气资源输送的可行性.Lourenco等［12］研究了外压作用下夹芯层材料对夹层管屈曲传播压力的影响.Castello等［13-14］对夹芯层与内外管之间黏合剂的黏结性能进行了实验研究，并建立了数值模型，分别采用接触面摩擦单元和弹簧单元2种方法模拟层间黏结性能，采用环模型分析了当外压和轴向弯曲共同作用时层间黏结性能对夹层管极限承载力的影响.An等［15］研究了夹芯层材料为钢纤维混凝土的夹层管在外压和轴向弯曲组合作用下的极限承载力，强调了钢纤维混凝土的侧向约束和层间黏结性能对夹层管静水压力-曲率承载力包络线具有较大的影响.Arjomandi等［16-19］分别考虑了夹芯层和内外管之间均无粘接、均完全粘接以及分别与内外管完全粘接4种情况，借助有限元数值模拟研究了外压和纯弯分别作用下夹层管的屈曲失稳性能.龚顺风等［20-21］基于实验与数值模拟相结合，研究了静水压力作用下管中管系统（pipe in pipe system）的屈曲传播，提出了更为精确的屈曲传播压力经验公式；假定夹芯层与内外管之间完全粘接，通过大量的数值模拟分析，阐述了截面初始几何缺陷、内外管径厚比、夹芯层厚度、钢材屈服强度和应变硬化特性等因素对夹层管屈曲失稳的影响机理.Xue等［22］采用一阶剪切变形理论研究了外压作用下夹层管的屈曲失稳特性，阐述了管道长细比、径厚比、夹芯层厚度等对夹层管屈曲失稳临界压力和截面屈曲失稳模态的影响.

本文通过进行切试件拉伸实验和夹层管段试件轴向推出实验，分别测得采用环氧树脂胶和3MDP8005胶在接触面光滑和粗糙条件下的层间切应力-位移关系曲线.基于实验测得的夹芯层与内外管之间的实际黏结性能，利用有限元软件ABAQUS建立纯弯作用下夹层管的三维数值分析模型，研究管道长度、截面几何构形、层间黏结性能、钢材等级和应变硬化参数等对夹层管屈曲失稳的影响.

1 层间黏结性能实验

对夹层管层间环向和轴向实际黏结性能分别进行实验研究.选用聚丙烯作为夹芯层材料，黏结剂分别采用环氧树脂胶和3M-DP8005胶，钢管接触面分别采用光滑和喷砂工艺，以模拟接触面不同的粗糙程度.

1.1 环向黏结滑移实验

设计简单的切试件拉伸实验来研究内外钢管与夹芯层之间的环向黏结性能，加载装置采用Zwick／Z010电子万能实验机，实验装置和试件如图1 所示.试件尺寸如图2所示，2片钢条通过黏结剂与中间的聚丙烯片粘接，在试件两端施加轴向拉力，直至钢条与聚丙烯片之间的粘接面发生切破坏.

钢条与聚丙烯片的接触面积较小，通常可假定应力在粘接面上均匀分布，因此，环向切应力τc可由下式求得：

式中：FT为试件所承受的拉力荷载，Ac为钢条与聚丙烯片单侧接触面的面积.试件最终破坏形态为单个切面失效，因此只须采用单个接触面面积.

图1 实验装置与试件示意图Fig.1 Schematic diagram of test equipment and specimens

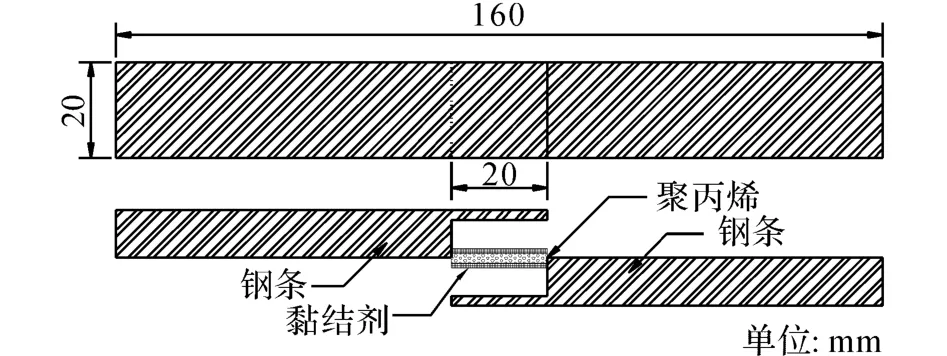
图2 环向黏结滑移试件尺寸Fig.2 Specimen dimensions for circumferential bondingslip test

钢条与聚丙烯片之间的4种粘接条件如下：1）黏结剂采用环氧树脂胶，钢条接触面光滑（记为ER Smooth）；2）黏结剂采用环氧树脂胶，接触面粗糙（记为ER Rough）；3）黏结剂采用3M-DP8005胶，接触面光滑（记为3M Smooth）；4）黏结剂采用3MDP8005胶，接触面粗糙（记为3M Rough）.每种粘接条件下各进行2组平行实验，取实验结果的平均值作为当前粘接条件下的黏结滑移曲线，代表夹层管内外钢管与聚丙烯夹芯层之间的环向黏结性能，结果如图3所示.图中，Δc为接触面相对位移.

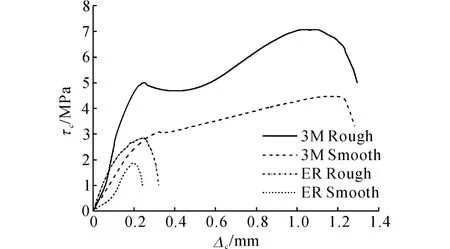
图3 环向黏结滑移实验结果Fig.3 Experimental results of circumferential bonding-slip

在层间采用环氧树脂胶、接触面喷砂的情况下，最大环向切应力为2.84MPa，相比接触面光滑时的环向切应力提升了49.5%；在采用3M-DP8005胶、接触面喷砂的情况下，最大环向切应力为7.07 MPa，相比接触面光滑时的环向切应力提升了58.2%.3M-DP8005胶的黏结性能明显优于环氧树脂胶的黏结性能，钢管与夹芯层之间的接触面采用喷砂工艺能较大幅度地提高层间环向黏结强度.

1.2 轴向黏结滑移实验

采用夹层管试件推出实验研究夹层管内外钢管和聚丙烯夹芯层之间的轴向黏结性能，加载装置采用INSTRON 8802液压伺服疲劳实验机，如图4所示.在试件两端施加压力荷载，直至夹芯层与外管、内壁之间的接触面发生轴向切破坏.内管和夹芯层齐平，高度低于外管，试件底部通过一个直径略小于外管内径的钢圆盘传递压力荷载.内外管采用SS304不锈钢材料，层间通过黏结剂粘接.夹层管试件的具体尺寸如图5所示.

图4 INSTRON 8802液压伺服疲劳实验机Fig.4 INSTRON 8802hydraulic servo fatigue testing system

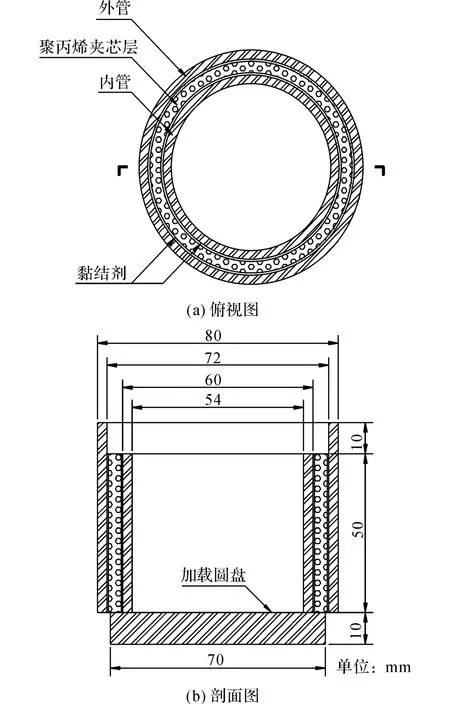
图5 轴向黏结滑移试件尺寸Fig.5 Specimen dimensions for axial bonding-slip test

假定应力在粘接面上均匀分布，则轴向切应力τa可表示为

式中：F 为试件承受的压力荷载，Di为夹芯层外径和外管内径的平均值，h为夹芯层的高度.外管与聚丙烯夹芯层之间采用4种粘接条件，粘结条件与环向黏结滑移实验完全相同，每种粘接条件下各进行2组平行实验，实验结果的平均值如图6 所示.图中，Δa为接触面的相对轴向位移.

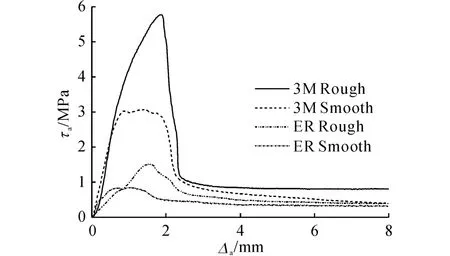
图6 轴向黏结滑移实验结果Fig.6 Experimental results of axial bonding-slip

实验结果表明：在接触面喷砂情况下，与接触面光滑情况相比，采用环氧树脂胶的最大轴向切应力提升了78.8%，层间黏结延性也有较大的提升；而在相同情况下采用3M-DP8005胶的最大轴向切应力和层间滑移分别提升了87.9%和32.2%.可以看出，3M-DP8005胶的轴向黏结强度和黏结延性明显优于环氧树脂胶，将钢管与夹芯层之间的接触面进行喷砂处理不仅能显著提高层间最大轴向切应力，还能增强黏结延性.

2 数值模拟

2.1 初始几何缺陷

在纯弯作用下，夹层管可能发生2种屈曲失稳模态，即极值型屈曲和分枝型屈曲.为研究不同的屈曲失稳模态，沿管道轴向引入褶皱型的初始几何缺陷，内外管沿轴向的半径变化量可通过下式描述：

式中：N 与λ 分别为沿管道轴向的褶皱波段数目和褶皱半波长，须通过合适的特征值分析确定［12］；L 为管道长度；Ri为外管或内管的平均半径；zi为第i个夹层管横截面距端截面的垂直距离；α0和α1为控制初始几何缺陷大小和不均匀度的参数.

根据管线钢管规范［23］要求，对于外径为168.275～609.600 mm （6.625～24.000in）的 管道，非管端截面允许的直径偏差为外径的0.75%，管端截面允许的直径偏差为外径的0.50%.取α0＝0.300%、α1＝0.075%，代入式（3），则夹层管跨中截面直径偏差为外径的0.75%，管端截面直径偏差为外径的0.45%，满足规范要求.取夹层管长度为外管外径的3倍，N＝5，将初始几何缺陷放大10倍，得到夹层管的初始几何形状如图7所示.

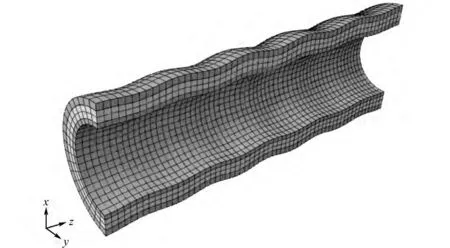
图7 夹层管轴向初始几何缺陷示意图Fig.7 Initial geometric imperfections of sandwich pipe in axial direction

2.2 材料的本构模型

本构模型的选取对于分析夹层管屈曲失稳具有较大的影响.一般而言，夹层管的内外管材料均采用碳锰钢，具有明显的屈服点和良好的塑性变形能力，通常采用Ramberg-Osgood（R-O）本构模型来描述其应力-应变关系：

式中：ε 为钢材正应变，σ 为钢材应力，E 为弹性模量，σy为有效屈服应力，n为应变硬化参数.

Ramberg-Osgood本构模型在应变较小时能较好地拟合钢材的应力-应变关系曲线.当应变较大时，采用该模型拟合得到的应力-应变曲线与实际值存在较大的偏差，因此，本文采用改进后的R-O 本构模型来拟合钢材的应力-应变关系曲线［24］.当ε＜1.5%时，仍采用式（4）描述其应力-应变关系；当ε≥1.5%时，则采用下式描述：

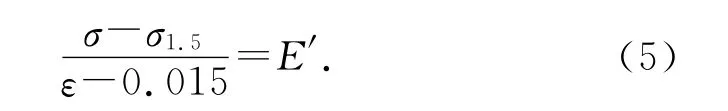
式中：σ1.5为应变为1.5%时钢材的应力.切线模量由下式表示：

以X65管线钢为例，分别采用R-O 本构模型和改进后的R-O 模型描述其应力-应变曲线，结果如图8所示.根据管线钢管规范［21］，σ0.5为X65管线钢在应变为0.5%时的应力.

图8 X65管线钢应力应变曲线Fig.8 Stress-strain curves for X65pipeline steel

聚丙烯是具有良好弹性变形的热塑性材料，其泊松比ν＝0.41.由于聚丙烯材料到达极限应力时对应的应变要远大于钢材的屈服应变，对聚丙烯夹芯层采用弹性建模可以在不影响精度的情况下，提高计算效率.

2.3 有限元模型

考虑到管道模型的对称性，取管道的1／4建立有限元模型.模型的边界条件如图9所示.在管道轴向的2个纵截面施加沿着y 轴方向的对称约束，在管道右侧端部截面施加沿着z 轴方向的对称约束.将左侧端部截面上的节点与圆心处参考点建立动态耦合关系，弯曲荷载的施加通过将转角施加在参考点上实现，并约束参考点的其他自由度，防止模型发生刚体位移.

随着端部截面转角θ的逐步增加，夹层管的弯曲曲率逐步增大，管道截面的平均曲率为

考虑到管道模型的对称性，可知L 的大小为模型长度的2倍.

图9 夹层管模型的边界条件Fig.9 Boundary conditions of sandwich pipe model

内外钢管单元类型选用27节点二次完全积分实体单元C3D27；由于聚丙烯材料的体积不可压缩性，夹芯层单元类型选用27节点二次完全积分杂交实体单元C3D27H，该类型单元能够克服切自锁问题，适用于接触类型的分析［25］.内外管沿厚度方向划分为1个单元，夹芯层沿厚度方向划分为2个单元，内外管和夹芯层沿环向划分为20个单元，沿轴向划分为30个单元，如图10所示.

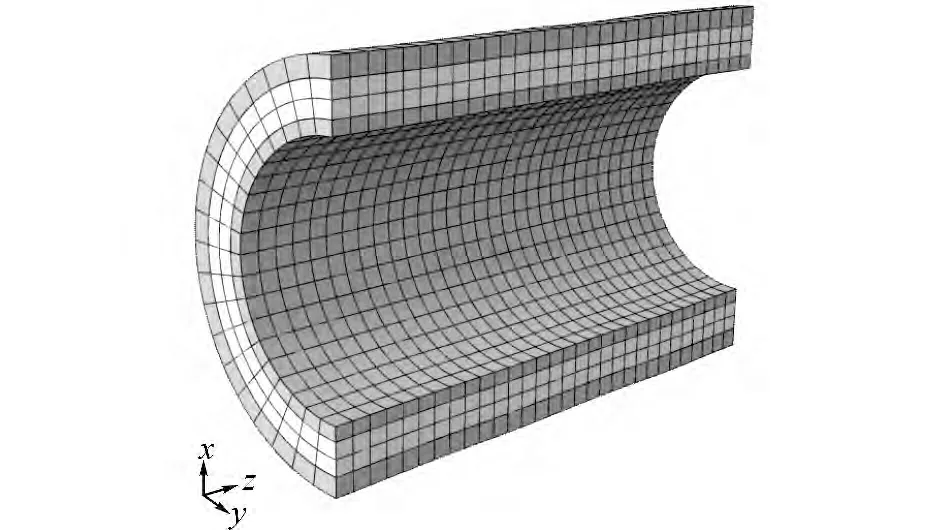
图10 夹层管有限元模型Fig.10 Finite element model of sandwich pipe

夹芯层与内外管接触面之间的轴向和环向黏结作用通过非线性弹簧来模拟.由于层间轴向和环向黏结性能的不相关性，有限元模型分别引入轴向和环向非线性弹簧来模拟层间黏结性能，弹簧采用SPRING2单元，弹簧受力根据节点的影响面积确定，其中环向和轴向弹簧的力-位移关系分别采用切试件和夹层管试件实验测得的切应力-位移关系曲线.同时，在夹芯层与内外钢管接触面之间建立面接触对，将内外管表面定义为主面，将接触面的法向相互作用定义为硬接触.夹层管屈曲失稳包含几何、材料和接触非线性，因此，在分析步设置时将几何非线性计算选项（Nlgeom）打开.此外，随着管道曲率的增大，在极值点附近，较小的曲率增量也会引起较大的变形，可以选择弧长法（Riks）进行计算，并采用自动增量控制.通过多次试算以及单元网格的敏感性分析，可以得到良好的收敛结果.

3 算例分析

若无特殊说明，算例模型内外管均采用API X65管线钢，夹芯层材料为聚丙烯，管道长度为外管外径的3倍；非线性弹簧采用接触面光滑、层间以3M-DP8005胶黏结性能实验测得的切应力-位移关系来模拟，其他参数如表1所示.弯曲作用下夹层管的变形及其Mises应力分布变化过程如图11所示.在弯曲加载初期，除去加载边界，应力沿夹层管轴向分布均匀，内外管应力水平基本一致，夹芯层应力水平相对较低.当跨中截面到达极限弯矩时，夹层管受压区沿轴向出现明显的波浪形褶皱，褶皱幅值从跨中到两端逐渐减小.在褶皱幅值较大的区域，夹芯层与内、外管接触面开始脱开，内外管跨中的受压区内壁出现应力集中现象.当继续增加转角位移时，夹层管平均曲率迅速增长，跨中截面出现较大的椭圆化变形，受压区层间粘接出现大面积失效，标志着夹层管已不适用于继续承载.在加载过程中夹芯层的应力始终保持在相对较低的水平，仍处于弹性阶段.

表1 算例模型的几何参数与材料特性Tab.1 Model geometric parameters and material properties of illustrative example

图11 加载过程中夹层管屈曲变形及应力分布Fig.11 Deformed configuration and stress distribution of sandwich pipe during loading process

4 参数分析

通过数值模拟对管道长度、层间黏结性能、内外管径厚比、夹芯层厚度、钢材等级和应变硬化等参数进行敏感性分析，以探究这些参数的不同取值对纯弯作用下夹层管屈曲失稳的影响，为夹层管道的设计提供理论基础.

4.1 管道长度

与单层管类似，夹层管在弯曲作用下的屈曲失稳受管道长度的影响比较显著.如图12所示为当管道长度分别为外管外径D 的1、3和5倍时，夹层管在弯曲作用下的屈曲失稳模态.

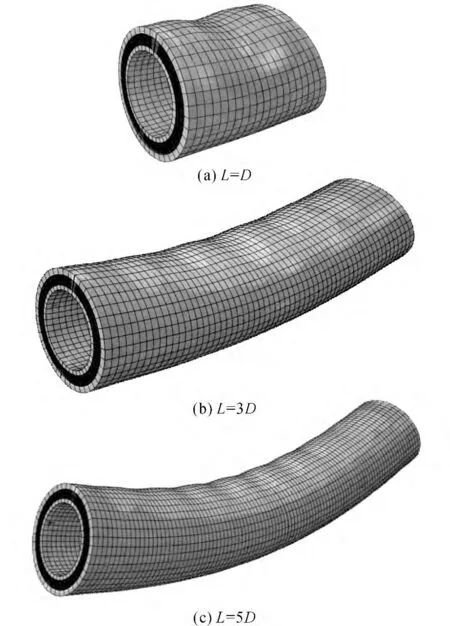
图12 不同长度夹层管的屈曲失稳模态Fig.12 Buckling and collapse modes of sandwich pipe with different lengths

当管道较短时，夹层管受压区出现明显的褶皱，表现为分枝型屈曲失稳破坏；随着管道长度的增加，夹层管跨中截面椭圆化变形增大，同时受压区出现褶皱，但不如短管的变化情况明显.

为便于分析，将夹层管的截面弯矩M 和平均曲率κ 分别对单层外管的截面屈服弯矩M0以及屈服曲率κ0进行归一化处理，M0和κ0可由下式计算：

式中：D0为外管的平均直径，t1为外管壁厚.

不同长度夹层管跨中截面弯矩M 与端部转角θ的关系如图13所示.归一化后，夹层管长度从L＝D 增至L＝7D，跨中截面极限弯矩Mc从2.59 M0降低到1.92 M0，对应的端部转角从0.14 增加到0.52.当L＝D 时，管道屈曲失稳性能受加载端边界条件影响较大，跨中截面极限弯矩明显高于极值型屈曲失稳.当L 从3D 增至7D 时，夹层管主要表现为极值型屈曲失稳，跨中截面的极限弯矩变化较小，而对应的端部转角随着管道的加长而增大.由于较大的端部转角将使管端承受更大的扭曲变形，会影响计算结果的精度，同时为提高计算效率，经综合考虑，选取夹层管长度L＝3D 开展后续参数分析.

图13 不同长度的夹层管截面弯矩与端部转角的关系Fig.13 Relationship between bending moment and rotation angle of sandwich pipes with different lengths

4.2 层间黏结性能

选取6种粘接情况进行参数分析：1）层间无粘接；2）接触面光滑，层间采用环氧树脂胶粘接；3）接触面粗糙，层间采用环氧树脂胶粘接；4）接触面光滑，层间采用3M-DP8005胶粘接；5）接触面粗糙，层间采用3M-DP8005胶粘接；6）完全粘接.将上述粘接情况与单层外管在弯曲作用下的屈曲失稳响应进行对比，结果如图14所示.

图14 不同层间黏结性能对应的夹层管截面弯矩与曲率关系曲线Fig.14 Bending moment-curvature curves of sandwich pipe for different inter-layer adhesion behaviors

在层间无粘接的情况下，相比单层外管，夹层管的极限弯矩提升了53.3%，对应曲率提升了34.0%.当层间采用环氧树脂胶粘接时，在接触面光滑和粗糙2种情况下，极限弯矩及其对应的曲率提升幅度较小.当层间采用3M-DP8005胶粘接时，当接触面粗糙时夹层管截面的极限弯矩及其对应的曲率与接触面光滑时相比分别提升了3.0%和5.9%.相比无粘接情况，在完全粘接的情况下，极限弯矩及其对应的曲率提升幅度分别达到了55.4%和262.7%.结果表明：在实际粘接情况下，夹层管截面极限弯矩及其对应的变形能力介于无粘接和完全粘接2种情况之间，且更接近于无粘接情况下的屈曲失稳性能.此外，黏结剂的切强度越高、内外管与夹芯层接触面越粗糙，对应的极限弯矩以及曲率越大.总的来说，层间黏结性能对弯曲作用下夹层管的屈曲失稳影响较小.

4.3 外管径厚比

取外管外径为558.800mm （22in），根据管线钢管规范［14］，分别取外管壁厚为36.525、28.575、22.225、19.050 和15.875 mm，对应的外管径厚比D1／t1为15.299、19.556、25.143、29.333和35.200.层间采用3M-DP8005胶粘接，接触面光滑，内管内径和壁厚保持不变.如图15所示为外管径厚比D1／t1对夹层管屈曲失稳的影响.

归一化前，D1／t1从15.299增加到35.200，夹层管跨中截面极限弯矩的降幅为36.3%.当屈曲失稳时，对应的曲率下降10.4%.外管径厚比对夹层管极限弯矩的影响较大，外管径厚比越大，极限弯矩越小，对应的曲率略有减小.归一化后，跨中截面极限弯 矩 从1.87 M0增 加 到2.54 M0，对 应 的 曲 率 从2.30κ0增加到5.13κ0.虽然，增大外管径厚比会降低夹层管的屈曲失稳性能，但是夹层管的极限弯矩以及曲率相对单层外管的提升效率有较大幅度的提高.

4.4 内管径厚比

图15 不同外管径厚比对应的夹层管截面弯矩与曲率关系曲线Fig.15 Bending moment-curvature curves of sandwich pipe for different diameter-to-thickness ratios of outer pipe

取内管外径为406.400mm （16in），内管壁厚分别取26.975、20.625、15.875、14.275 和11.913 mm，对应的内管径厚比D2／t2为15.066、19.704、25.600、28.470和34.115.层间采用3M-DP8005胶粘接，接触面光滑，外管外径和壁厚保持不变.如图16所示，D2／t2从15.066增加到34.115，夹层管跨 中 截 面 极 限 弯 矩 分 别 为2.20 M0、1.99 M0、1.85 M0、1.80 M0和1.74 M0，降 幅 为20.9%，对 应的平均曲率分别为3.25κ0、2.86κ0、2.54κ0、2.52κ0和2.41κ0，降幅为25.8%.由此可知，内管径厚比越大，夹层管的极限弯矩以及屈曲失稳时的变形能力越小，且D2／t2对夹层管屈曲失稳性能的影响也越小，与外管径厚比相比，内管径厚比对夹层管极限弯矩的影响相对较小.

4.5 夹芯层厚度

取外管外径为558.800 mm（22in），壁厚为28.575mm，径厚比D1／t1＝19.556.通过改变内管外径来实现不同的夹芯层厚度，并控制内管径厚比D2／t2≈20.000，以避免内管径厚比变化对结果造成影响.如图17所示，D2／D1从0.489增至0.818，夹芯层逐渐变薄，夹层管的极限弯矩分别为2.54 M0、2.19 M0、2.05 M0、1.99 M0和1.97 M0，降 幅 为22.4%，对应 的平均曲率分别为7.95κ0、4.85κ0、3.88κ0、2.86κ0和2.16κ0，降幅达72.8%.结果表明：夹芯层越厚，夹层管极限弯矩越大，屈曲失稳前的变形能力越强，而且失稳后弯矩下降也越平缓.

图16 不同内管径厚比夹层管对应的截面弯矩与曲率关系曲线Fig.16 Bending moment-curvature curves of sandwich pipe for different diameter-to-thickness ratios of inner pipe

图17 不同夹芯层厚度夹层管对应的截面弯矩与曲率关系曲线Fig.17 Bending moment-curvature curves of sandwich pipe for different thicknesses of core layer

4.6 钢材等级

根据管线钢管规范［14］，分别选取X60、X65、X70和X80 管线钢来分析内外管钢材等级对弯曲作用下夹层管屈曲失稳性能的影响，内外管钢材屈服强度分别为414、448、483和552 MPa.

内管选用X65管线钢，外管钢材等级从X60提升至X80，对应的夹层管截面弯矩与曲率关系曲线如图18所示.归一化前，夹层管跨中截面极限弯矩分别为3 402、3 576、3 758 和4 118kN·m，增大21.0%，屈曲失稳时对应的平均曲率分别为0.289、0.290、0.274和0.267m-1，略有下降.归一化后，跨中截面极限弯矩分别为2.05 M0、1.99 M0、1.94 M0和1.86 M0，下降了9.3%，对应曲率分别为2.85κ0、2.86κ0、2.70κ0和2.63κ0，下降了7.7%.以上结果表明：外管钢材等级越高，夹层管的极限弯矩越大，但屈曲失稳前的变形能力略有下降，同时夹层管的屈曲失稳性能的提升幅度低于单层外管的屈曲失稳性能提升幅度.

图18 不同外管钢材等级对应的夹层管截面弯矩与曲率关系曲线Fig.18 Bending moment-curvature curves of sandwich pipe for different steel grades of outer pipe

外管选用X65管线钢，内管钢材等级从X60提升至X80，对应的夹层管截面弯矩与曲率关系曲线如图19 所示.夹层管跨中截面极限弯矩分别为1.95 M0、1.99 M0、2.02 M0和2.10 M0，提升7.7%，对应的平均曲率分别为2.84κ0、2.86κ0、2.74κ0和2.73κ0，变化较小.可以看出，提升内管钢材等级也能提高夹层管的极限弯矩，但其提升效果不如提升外管钢材等级的效果明显.

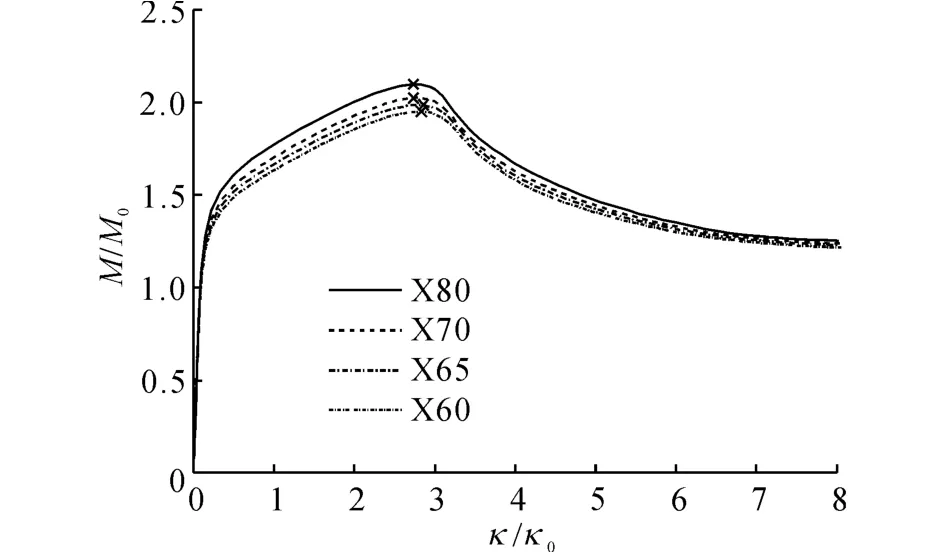
图19 内管不同钢材等级夹层管截面弯矩与曲率关系曲线Fig.19 Bending moment-curvature curves of sandwich pipe for different steel grades of inner pipe

当内外管钢材等级从X60同步提升至X80时，对应的夹层管截面弯矩与曲率关系曲线如图20所示.归一化前，夹层管跨中截面极限弯矩分别为3 338、3 576、3 824和4 319kN·m，增幅为29.4%，对应的 平 均 曲 率 分 别 为0.290、0.290、0.275 和0.266m-1，下降8.3%.归一化后，夹层管跨中截面极限 弯 矩 分 别 为2.01 M0、1.99 M0、1.97 M0和1.95 M0，呈下降趋势，但变化较小，对应曲率分别为2.85κ0、2.86κ0、2.70κ0和2.63κ0.由此可知，对于夹层管极限弯矩，同时提升内外管钢材等级比单独提升内管或外管钢材等级更加有效，与单层外管相比，夹层管屈曲失稳性能的提升效率随内外管钢材等级的提高而略有降低.

图20 不同内、外管钢材等级对应的夹层管截面弯矩与曲率关系曲线Fig.20 Bending moment-curvature curves of sandwich pipe for different steel grades of outer pipe and inner pipe

4.7 应变硬化参数

图21 不同应变硬化参数夹层管对应的截面弯矩与曲率关系曲线Fig.21 Bending moment-curvature curves of sandwich pipe for different strain hardening parameters

如图21所示为钢材的应变硬化参数n 对弯曲作用下夹层管屈曲失稳性能的影响.内外管钢材应变硬化参数n 分别取7、13和30，夹层管跨中截面极限弯矩分别为2.44 M0、1.99 M0和1.69 M0，下降30.7%，对应曲率分别为2.67κ0、2.86κ0和2.50κ0.可以看出，钢材的应变硬化参数越小，夹层管在弯曲作用下的极限弯矩越大.在弯曲作用下，钢材的应变硬化可以得到充分的发挥，因而应变硬化参数对夹层管的屈曲失稳性能有较大的影响.

5 结 论

（1）3M-DP8005 胶的轴向和环向黏结强度和黏结延性均优于环氧树脂胶，将钢管与夹芯层之间的接触面进行喷砂处理能较大幅度地提升轴向与环向的黏结强度，还能增强轴向黏结延性.

（2）夹层管在弯曲作用下的屈曲失稳性能以及屈曲失稳模态受管道长度的影响较大.当管道较短时，破坏特征表现为受压区产生较大的褶皱；而当管道较长时，破坏特征表现为跨中截面出现较大的椭圆化变形，同时受压区沿轴向产生轻微的褶皱.

（3）在相同外管尺寸下，夹层管在弯曲作用下的极限弯矩以及屈曲失稳前的变形能力均优于传统的单层管.

（4）在实际粘接情况下，夹层管的屈曲失稳性能介于层间无粘接和完全粘接2种情况之间，且更接近于无粘接情况下的屈曲失稳性能，黏结剂的切强度以及接触面的粗糙程度对弯曲作用下夹层管的屈曲失稳性能影响较小.

（5）夹层管截面几何构形对极限弯矩以及屈曲失稳前的变形能力影响较大.内外管径厚比越大，夹层管的极限弯矩越小，与内管径厚比相比，外管径厚比产生的影响更大.夹芯层越厚，夹层管的屈曲失稳性能越强，同时夹芯层厚度对夹层管屈曲失稳性能的影响也越显著.

（6）内外管钢材的材料特性对夹层管的屈曲失稳性能有较大的影响.提升外管或内管的钢材等级都能够提高夹层管的极限弯矩，并且同时提升内外管的钢材等级对提高夹层管的极限弯矩更为有效.钢材的应变硬化参数越小，夹层管的极限弯矩越大.

（

）：

［1］KYRIAKIDES S，CORONA E.Mechanics of offshore pipelines，volume 1：buckling and collapse［M］.Oxford and Burlington：Elsevier Science，2007.

［2］GONG S F，YUAN L，JIN W L.Buckling response of offshore pipelines under combined tension，bending，and external pressure［J］.Journal of Zhejiang University：Science A，2011，12（8）：627-636.

［3］龚顺风，陈源，金伟良，等.高静水压力作用下深海油气管道的局部屈曲［J］.浙江大学学报：工学版，2012，46（1）：14-19.GONG Shun-feng，CHEN Yuan，JIN Wei-liang，et al.Local buckling of deepwater oil-gas pipeline under high hydrostatic pressure［J］.Journal of Zhejiang University：Engineering Science，2012，46（1）：14-19.

［4］余建星，卞雪航，余杨，等.深水海底管道全尺寸压溃实验及数值模拟［J］.天津大学学报，2012，45（2）：154-159.YU Jian-xing，BIAN Xue-hang，YU Yang，et al.Fullscale collapse test and numerical simulation of deepwater pipeline［J］.Journal of Tianjin University，2012，45（2）：154-159.

［5］赵冬岩，余建星，岳志勇，等.含缺陷海底管道屈曲稳定性的数值模拟［J］.天津大学学报，2009，42（12）：1067-1071.ZHAO Dong-yan，YU Jian-xing，YUE Zhi-yong，et al.Numerical simulations on buckling stability of subsea pipelines with imperfections［J］.Journal of Tianjin University，2009，42（12）：1067-1071.

［6］XUE J.Local buckling in infinitely，long cylindrical shells subjected uniform external pressure［J］.Thin-Walled Structures，2012，53：211-216.

［7］XUE J，YUAN D，HAN F，et al.An extension of Karman-Donnell’s theory for non-shallow，long cylindrical shells undergoing large deflection［J］.European Journal of Mechanics-A／Solids，2013，37：329-335.

［8］ZHENG J，PALMER A，BRUNNING P，et al.Indentation and external pressure on subsea single wall pipe and pipe-in-pipe［J］.Ocean Engineering，2014，83（6）：125-132.

［9］RAMASAMY R，YA T T.Nonlinear finite element analysis of collapse and post-collapse behaviour in dented submarine pipelines［J］.Applied Ocean Research，2014，46（11）：116-123.

［10］KARDOMATEAS G A，SIMITSES G J.Buckling of long sandwich cylindrical shells under external pressure［J］.Journal of applied mechanics，2005，72（4）：493-499.

［11］ESTEFEN S F，NETTO T A，PASQUALINO I P.Strength analyses of sandwich pipes for ultra deepwaters［J］.Journal of Applied Mechanics，2005，72（4）：599-608.

［12］LOURENCO M I，PASQUALINO I P，DA SILVA PALERMO T.Core material performance on the propagation pressure of sandwich pipes［C］∥Proceeding of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering.Estoril：American Society of Mechanical Engineers，2008：471-480.

［13］CASTELLO X，ESTEFEN S F.Sandwich pipes for ultra deepwater applications［C］∥Offshore Technology Conference.Houston：Offshore Technology Conference，2008：2093-2101.

［14］CASTELLO X，ESTEFEN S F.Limit strength and reeling effects of sandwich pipes with bonded layers［J］.International Journal of Mechanical Sciences，2007，49（5）：577-588.

［15］AN C，CASTELLO X，DUAN M L，et al.Ultimate strength behaviour of sandwich pipes filled with steel fiber reinforced concrete ［J］.Ocean Engineering，2012，55（4）：125-135.

［16］ARJOMANDI K，TAHERI F.The influence of intralayer adhesion configuration on the pressure capacity and optimized configuration of sandwich pipes［J］.Ocean Engineering，2011，38（17）：1869-1882.

［17］ARJOMANDI K，TAHERI F.A new look at the external pressure capacity of sandwich pipes［J］.Marine Structures，2011，24（1）：23-42.

［18］ARJOMANDI K，TAHERI F.Stability and post-buckling response of sandwich pipes under hydrostatic external pressure［J］.International Journal of Pressure Vessels and Piping，2011，88（4）：138-148.

［19］ARJOMANDI K，TAHERI F.Bending capacity of sandwich pipes［J］.Ocean Engineering，2012，48（3）：17-31.

［20］GONG S F，LI G.Buckle propagation of pipe-in-pipe systems under external pressure ［J］.Engineering Structures，2015，84：207-222.

［21］龚顺风，胡勍.外压作用深海夹层管复合结构屈曲失稳分析［J］.浙江大学学报：工学版，2014，48（9）：1624-1631.GONG Shun-feng，HU Qing.Buckling and collapse analyses of composite structures for deepwater sandwich pipes under external pressure［J］.Journal of Zhejiang University：Engineering Science，2014，48（9）：1624-1631.

［22］XUE J，WANG Y，YUAN D.A shear deformation theory for bending and buckling of undersea sandwich pipes［J］.Composite Structures，2015，132：633-643.

［23］American Petroleum Institute（API），API specification 5L／ISO 3183.specification for line pipe［S］.45th ed.Washington D C：API Publishing Services，2013.

［24］GONG S F，SUN B，BAO S，et al.Buckle propagation of offshore pipelines under external pressure［J］.Marine Structures，2012，29（1）：115-130.

［25］HIBBIT H D，KARLSSON B I，SORENSEN P.ABAQUS theory manual ［M］.6th ed.Pawtucket：Hibbitt，Karlsson and Sorensen（HKS）Inc，2010.