一种图像的连续性边缘提取方法*

贾 迪，董 娜，孟祥福，李思慧，陈 硕

(1.辽宁工程技术大学电子与信息工程学院，辽宁 葫芦岛 125105; 2.国网辽宁省电力有限公司信息通信分公司，辽宁 沈阳 110006)

1 引言

边缘检测是进行图像信息提取和模式识别的基础，是图像处理领域的重要内容。边缘是指其周围像素灰度有阶跃变化像素的集合。边缘广泛存在于物体与背景、物体与物体之间，它的出现是由于存在不连续的区域性灰度造成的。图像中往往包含很多信息，即便是很简单的景物图像中也包含了大量细节，在图像中表现为强度的非连续性。

早期的边缘检测算法有微分法、模板匹配法、门限化法等[1]。近年来，随着人工智能与数学的发展，出现了许多新的边缘检测方法，如偏微分方程的方法[2,3]、基于多尺度融合技术的方法[4]、基于改进的某种算子、梯度的方法[5]、多层次高斯小波法[6,7]等。基于偏微分方程法提取的边缘连续性好，但迭代收敛速度慢，其收敛速度对嵌入函数的初始位置依赖性很强。文献[4]根据边缘检测离散准则设计平滑滤波算子，将其与嵌入可信度方法相结合进行边缘检测，算法具备一定的抗噪性与连续性，但对于结构较为复杂的图像连续性较差。文献[5]提出一种基于改进的形态学算子的边缘检测算法，用于保留更多的边缘细节，实验结果表明，该方法提取的边缘连续性较差。文献[6]利用小波分解后的图像低频部分用提出的8点邻域自适应梯度算法进行边缘检测，与Canny算法相比，该方法具有较好的连续性，但依然存在断裂部分。文献[7]提出一种基于边缘方向性的平滑算法，并与小波方法结合进行边缘检测，但该算法对方向性不强的图像效果不明显。

本文提出一种图像的连续性边缘提取方法，一方面采用微分法中Canny算子处理图像获得边缘检测结果，完成边缘定位，利用边缘检测结果生成边缘膨胀图;另一方面以膨胀图为基础生成平均曲率运动MCM(Mean Curvature Motion)方程[8,9]的嵌入函数，通过迭代完成图像的边缘提取。该方法结合了微分法与偏微分方程法的优点，可以在较短的时间内完成图像的连续性边缘提取，为图像后续处理提供帮助。

2 基础算法简介

2.1 Canny算法

Canny算法是 John C 于1986年提出的，它与Marr(LoG)边缘检测方法类似，采用先平滑后求导的方法经过四个步骤的处理获得图像边缘部分：

(1)用高斯滤波器平滑图像；

(2)用一阶偏导有限差分计算梯度幅值和方向；

(3)对梯度幅值进行非极大值抑制；

(4)用双阈值算法检测和连接边缘。

尽管如此，由于该算法是一种基于算子的操作，因此不可避免地产生非连续性边缘，无法直接应用于图像的后续分割、测量等处理。

2.2 MCM方程

平均曲率运动方程(MCM)是一种Euclidean几何不变流，如式(1)所示：

(1)

其中，C为进化曲线，t为时间，k为曲线曲率，N为曲线的法向量。文献[8,9]讨论了该方程的基本性质，它不仅满足旋转、平移、均匀缩放三重不变性，而且曲线的封闭性与连通性也将保持不变。

3 算法设计

3.1 算法处理流程

本文主要算法流程分为六个步骤，其中膨胀图与MCM方程的嵌入函数的生成过程在3.2与3.3节中进行介绍，算法具体执行流程如图1所示。

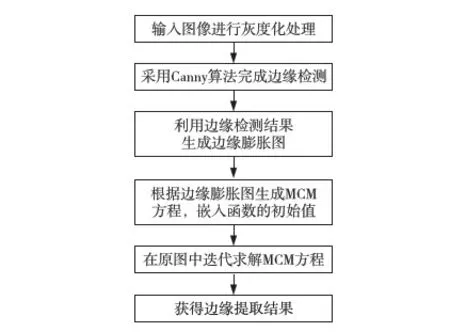
Figure 1 Process of image continuous edge extraction图1 图像连续性边缘提取流程

3.2 边缘膨胀图

图2给出了采用Canny算子提取图像边缘的结果。图2a由两种灰度构成，由于图像结构较为简单，因此Canny算子可以较好地完成边缘提取。在结构复杂的图像中，采用这种算子提取边缘很容易产生非连续性边缘，假设图2b中给出的A、B、C三个位置存在断裂，如何弥补这种不足是本文研究的重点。

Figure 2 Processing result analysis of Canny algorithm图2 Canny算法处理结果分析

图3由两条线段构成，定义所有线段的末端为A类区域，线段的非末端区域为B类区域。为了弥补线段断裂区域，采用半径为R的圆形模板对A类区域进行膨胀操作，当R足够大时，两条线段的断裂区域将被连接。通常R可以根据需要取2、3、4几种值，不宜过大，因为半径越大，膨胀后的边缘离真实边缘距离越远，后续MCM模型迭代收敛的时间也就越长。线段的B类区域为图像的连续边缘，但为了配合MCM方程的曲率运动，需要构造一个边缘区域，该区域可作为生成内部与外部初始化嵌入函数的基础，因此同样需要对B类区域进行膨胀操作，选择r做为该类区域的圆形膨胀半径，取值大于1即可满足上述条件。

Figure 3 Analysis of expansion processing图3 膨胀处理分析

为了获得整幅图像的A、B类区域，首先需要确定哪些点是线段末端，哪些不是，相关情况如图4所示。

Figure 4 Combination of pixels at the end of edge图4 边缘末端像素组合

图4a～图4h给出了以中心像素为末端的所有组合情况。令原始图像为I，经Canny算子处理后的图像为Ic，新的膨胀图为Ip， 确定边缘像素后，以该像素为中心、R为半径在Ip中进行膨胀操作，其它线段部分以r为半径在Ip中进行相同操作，具体实现过程伪代码如下：

ProcedureExpand(InputIc,R,r,Output:Ip){

sizeof(Ic,&m,&n);//求取图像的长与宽

memset(Ip,0,m*n);//将Ip内的像素置0

fori=4:m-4

forj=4:n-4

{

k=0;

if (Ic(i,j) >0)

forbi=-1:1

forbj=-1:1

{//统计区域内的非0像素数量

if (Ic(i+bi,j+bj)>0)

k++;

}

if (k==1)//边缘末端点的膨胀处理

forbi=-R:R

forbj=-R:R

Ip(i+bi,j+bj)=255;

else

if (k>1) //边缘的膨胀处理

forbi=-r:r

forbj=-r:r

Ip(i+bi,j+bj)= 255;

}

}

End

经过上述过程处理，新获得的Ip图像即为膨胀图，它由0与255两种灰度构成。经过膨胀处理后的图像通常可以弥补由Canny算子造成的断裂边缘部分，从而为下一步MCM方程的迭代求解打下基础。

3.3 边缘膨胀图

根据膨胀图的特点，可以通过简单的算法，直接确定区域的内部及外部边缘，以此作为MCM方程嵌入函数的初始值。MCM方程是一种基于线性几何热流理论的方程，进化过程保持曲线的封闭性与连通性。经典MCM方程进化过程没有考虑目标边缘的阻力问题，因此引入如下g函数增加图像边缘部分的阻力系数：

(2)

(3)

(4)

其中，g为关于曲率的函数，f为曲率项，Ix、Iy为一阶微分，Ixx、Iyy为二阶微分。如图5所示，通过调节反差参数K，可以获得不同的曲率调节度，获得理想的阻力曲线，从而控制g的下降速度[10]。式(2)中，C为一条平面封闭曲线，将它定义为二维函数u(x,y)的水平集C={(x,y),u(x,y)=c}，则C有某种变化，可以归结为是由函数u(x,y)发生某种变化引起的，借助数值计算可以计算它的数值解[8]：

(5)

Δu=uxx+uyy

(6)

(7)

上式的半隐式方案求解如下所示：

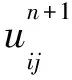
(8)

(9)

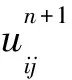
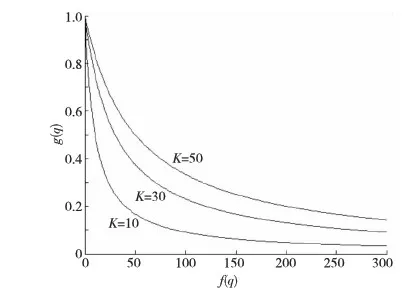
Figure 5 Influence of contrast parameter K on g function图5 反差参数K对g函数的影响

(10)

由于这种方法已经使迭代边缘位于原图边缘附近，因此可以通过较少次迭代完成边缘提取，同时由于MCM模型具有自合并分离特性，因此可以合并距离图中的琐碎区域，从而以较好的粒度保证了图像分割的尺度。图6为图2a边缘提取过程的放大结果。

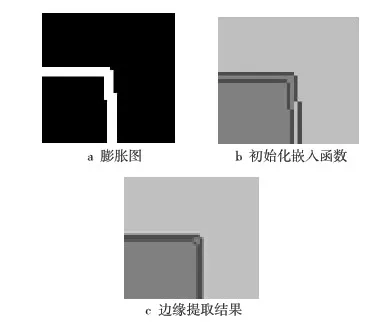
Figure 6 Process of edge extraction图6 边缘提取过程

3.4 实验结果与分析

选用CPU主频为3.6 Hz，内存2 GB的计算机作为实验环境。选择景色、人物、建筑三种不同类别的彩色图像作为实验对象，图像大小依次为128×128、256×256、512×512。实验参数的设置中，令R=3、r=1、τ=4、迭代次数n=40，实验结果如图7～图9所示。

Figure 7 Contrast of experimental results 1图7 实验结果对比1

Figure 8 Comparison of experimental results 2图8 实验结果对比2

Figure 9 Comparison of experimental results 3图9 实验结果对比3

图7a～图7f是一组景物类图像的实验结果对比。图7a为原始图像，图7b为采用Canny算法提取边缘的结果，图7c为相应的膨胀图。可以看到，膨胀图已经填充了图7b中断裂的边缘区域。图7d以图7c为基础，构造了MCM方程的初始嵌入函数值，并通过该方程的迭代获得图7e的最终边缘提取结果。对比图7e与图7b，图7e中花朵边缘的提取的连续性较好，不存在断裂问题。由于引入了边缘停止函数，使得最后的边缘提取结果与实际边缘吻合。图8为一组人物类图像的实验结果。对比图8e与图8b中的箭头指示区域，图8e已经将断裂处进行了连接，并且通过MCM方程的迭代求解，将梯度较弱的琐碎区域经行了合并处理，突出了图像中目标区域的边缘部分。图9为一组建筑类的图像实验结果对比。与图9b的Canny算法处理结果相比，本文方法不仅将断裂处进行了有效连接，同时避免了琐碎区域的边缘提取，如凯旋门上左右两侧的石狮。各组实验结果的局部区域放大对比如图7f、图8f和图9f所示。表1给出了三组实验的算法处理时间对比。随着图像尺寸的增加，Canny算法始终将处理时间控制在1 s以内。本文算法是以Canny算法为基础，增加了膨胀图与MCM方程的求解，因此速度较慢，且在大尺寸的图像处理中耗时较多，因此该方法适合处理图像尺寸较小或对处理时间要求较宽松的环境。

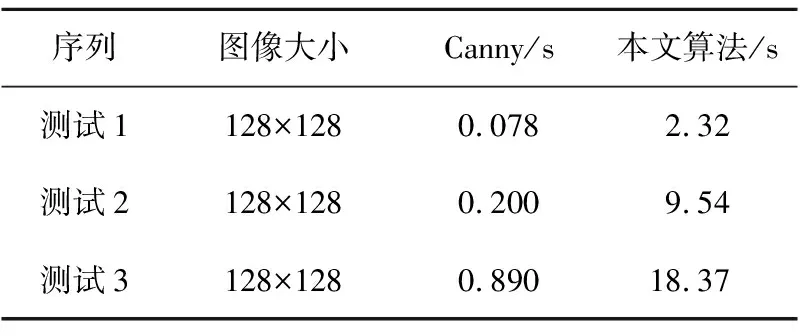
Table 1 Contrast of algorithm execution

4 结束语

针对图像的连续性边缘提取问题，本文提出一种结合Canny算子与MCM方程的图像边缘提取方法。首先采用Canny算法对图像进行边缘检测，根据检测结果构造膨胀图。膨胀模板的选择分为两种情况：一种根据本文给出的算法探测边缘“断裂”处，并采用半径为R的圆形模板进行填充；另一种选择半径为r的圆形模板对剩余边缘检测结果进行膨胀处理，为MCM模型的迭代求解奠定基础。其次通过膨胀图构造了MCM方程的初始嵌入函数u，最后引入边缘停止函数改进MCM方程，通过迭代求解获得最终的边缘提取结果。本文方法能够较好地获取图像的连续性边缘，实验结果验证了本文算法的有效性。

[1] Gonzalez R C, Woods R E. Digital image processing[M]. Third Edition. Beijing:Electronic Industry Press, 2011.(in Chinese)

[2] Wen Pei-zhi, Huang Jin-fang, Ning Ru-hua, et al. Boundary extraction of active contour based on tensor voting[J]. Computer Engineering,2012, 38(6):216-218.(in Chinese)

[3] Yu Xiao-sheng,Wu Cheng-dong,Chen Dong-yue,et al.Gradient vector flow geodesic active contour model based on edge preserving diffusion[J]. Journal of Northeastern University, 2013, 34(5):642-645.(in Chinese)

[4] Lian Jing, Wang Ke. Image edge detection based on multi-scale fusion technology[J].Chinese Journal of Scientific Instrument,2007,28(5):853-858.(in Chinese)

[5] Meng Ting-ting, Yu Liang, Li Shou-min, et al. An edge detection algorithm based on improved morphologic operators[J]. Computer Engineering & Science,2011,33(8):112-116.(in Chinese)

[6] Jin Huan-di, Wang Jun-feng, Zhang Xu-bo, et al. An adaptive gradient edge detection algorithm based on wavelet transformation[J].Computer Engineering & Science,2011,33(8):117-121.(in Chinese)

[7] Yuan Xiu-gui, Gong Zheng, Meng Zheng-zhong. A wavelet transform-based edge detection algorithm based on edge direction[J]. Computer Engineering & Science,2010,32(3):49-51.(in Chinese)

[8] Sapiro G.Affine invariant scale space[J].International Journal of Computer Vision, 1993, 11(1):25-44.

[9] Caselles V, Kimmel R, Sapiro G. Geodesic active contours[J]. International Journal of Computer Vision, 1997, 22(1):61-79.

[10] Wang Da-kai, Hou Yu-qing, Peng Jin-ye. Method of partial differential equation in image processing[M]. Beijing:Science Press,2008.(in Chinese)

附中文参考文献：

[1] 冈萨雷斯，伍兹. 数字图像处理[M].第3版. 北京：电子工业出版社, 2011.

[2] 温佩芝，黄锦芳，宁如花,等.基于张量投票的主动轮廓边缘提取[J].计算机工程,2012,38(6):216-218.

[3] 于晓升，吴成东，陈东岳,等.基于边缘保护扩散的梯度矢量流测地线活动轮廓模型[J].东北大学学报(自然科学版),2013,34(5):642-645.

[4] 连静,王珂.基于多尺度融合技术的图像边缘检测[J].仪器仪表学报, 2007, 28(5):853-858.

[5] 孟婷婷,余谅,李寿敏,等.一种基于改进的形态学算子的边缘检测算法[J].计算机工程与科学,2011,33(8):112-116.

[6] 靳焕娣,王军锋,张旭勃.基于小波变换的自适应梯度边缘检测算法[J].计算机工程与科学,2011,33(8):112-116.

[7] 袁修贵,龚正,孟正中.基于边缘方向性的小波边缘检测算法[J].计算机工程与科学,2010,32(3):49-51.

[10] 王大凯,候榆青,彭进业. 图像处理的偏微分方程方法[M]. 北京：科学出版社, 2008.