低空间复杂度的LSH算法及其在图像检索中的应用*

曹玉东，刘艳洋，孙福明，贾 旭

(辽宁工业大学电子与信息工程学院，辽宁 锦州 121001)

1 引言

为了提高图像检索速度，最好的办法就是建立索引。众多研究者已经给出了大量的索引方法，例如TBBF[1]、iDistanc[2]和R-tree[3]等都能在一定程度上克服维数灾难，较好地解决了高维数据搜索问题。BBF保持kd-tree的二叉平衡树索引结构不变，在数据搜索的回溯查询阶段，引入一个优先查找队列，极大地提高了kd-tree的查找性能。iDistance索引方法认为如果两个高维向量相似，那么它们到某个参考点的距离也相似。基于该思想，iDistance把特征集合聚类，每个分类被看作是一个以质心为中心的超球体，给定查询点及其查询半径，通过三角不等式确定在各个类中的查询范围。R-tree把一个多维对象只分到一个子空间中，构成一棵平衡树，随后R-tree的变种也相继出现，但是当特征维数高于10时，R-tree就会因为重叠超矩形空间和死区的大量存在而导致性能严重下降，甚至不如顺序搜索(即将查询点逐一同数据库中所有的元素做比较，也称为线性搜索或穷尽搜索)。前面提到的其它索引算法也不同程度地存在此问题。 局部敏感哈希LSH(Locality Sensitive Hashing)索引[4]则完全从另外一个角度建立索引结构，先将数据库中的高维数据点投影到某个特征空间；然后从哈希函数簇中随机选择k个不同的哈希函数，将每个数据点映射为一个k维矢量， 相似的数据点可能会被量化为同一个k维矢量，这样的数据点会散列到同一个哈希桶中，查询时对输入的数据点做相同的散列，穷举搜索与查询点发生冲突的桶，将会以较大的概率得到查询点的近邻。为避免边界的影响，增加找到真实近邻的概率，可以重复以上操作几次。实验数据表明，LSH算法无论是在匹配速度还是匹配精度上，都具有明显的优势[5]。现在LSH算法已经成功地应用到图像检索[6]、音频检索[7]和文本检索[8]等领域。

国内一些研究人员也提出了一些改进的LSH算法，如文献[9]利用数据集的统计特性运用迭代的方法从随机生成的若干哈希函数中选择出更合适的哈希函数，从而提高了LSH算法的性能，但其离线训练时间明显增加。文献[10]提出了多次随机子向量量化哈希算法，根据随机抽取的特征子向量构建哈希函数，但是其实验仅仅在包含大约一万幅图像的数据库上进行。计算技术的进步导致海量数据出现在因特网上，本文旨在降低标准LSH算法的空间复杂度，使用较少数量的哈希表构造高维数据的索引结构，同时不降低算法的性能，这对大规模的高维数据搜索任务是有意义的。

2 图像的特征提取

表达图像的原始数据往往是庞大和无序的，通常只考虑了存储和传输的要求，为了挖掘隐藏在图像原始数据中的规律性特征和本质性特征，需要在图像的内容层次设计图像特征的表达方法，常见的图像特征表示方法可以分为两种，一是基于特征袋(Bag of Features)表示[11]，另一个是使用全局描述算子表示。特征袋表示法一般用若干局部特征构成的集合来表示图像，适合使用倒排文档索引组织数据；图像的全局特征通常是一个高维矢量。本文使用Gist特征[12](全局描述算子的一种)表示图像。文献[13]指出图像的Gist特征已经在图像检索应用中取得了很好的效果。Gist特征描述了一系列感知维度，包括自然度(Naturalness)、开放度(Openness)、粗糙度(Roughness)、扩展度(Expansion)和光滑度(Ruggedness)。这些感知维度代表了场景的空间结构，可以通过谱变换和粗略的局部定位信息估计出来。令图像通过一组Gabor滤波器(在三个尺度上的方向数分别是2、4、4)，将图像分成2×2个无重叠的窗口，在每个窗口中提取出方向柱状图，这样每幅图像用(2+4+4)×4=40维的Gist特征来表示。

3 LSH算法

LSH算法的基本思想就是用随机的哈希函数值保证相似的数据点以很高的概率发生冲突而能够被检测到[4]。哈希函数是单向的散列函数，它将目标的表示映射为更简单的形式，在LSH算法中，哈希函数满足:

Prh∈H[h(u)=h(v)]=sim(u,v)

(1)

其中，H是哈希函数簇，哈希函数h从H中均匀地选取，把一个向量映射为一个数，u和v是两个高维的数据点，sim(u,v)∈[0,1]是相似度函数。

给定一个查询点，LSH算法能够在远小于穷举搜索的时间内搜索到近似近邻。尤其在数据库的规模很大的时候，其优势十分明显。

3.1 算法描述

标准LSH索引高维数据的过程如下所述，使用哈希函数把数据库中的矢量点投影到随机的方向矢量ai上。ai的每个元素服从p-稳定分布(当p=2时是标准高斯分布)。

哈希函数定义为：

(2)

其中，w是投影的量化宽度;b的取值服从[0,w]的均匀分布,参数b增强了哈希函数的随机性，可能有利于消除哈希桶边界的影响。内积ai·p就是数据点p在ai上的投影。经过取整操作，哈希函数的值被量化为一个整数。单个哈希函数的区分性较弱，因此需要构建第二级哈希函数，它也被称为局部敏感哈希函数LSH，其形式为：

gj(p)={hj,1(p),…,hj,k(p)},j=1,…,l

(3)

其中，k的值远远小于数据点的维数，由k个整数构成的矢量也被称为哈希码，它可以看作是数据点p的降维表示。每一个gi对应一个哈希表，高维数据点经过gi映射为k维哈希码，具有相同哈希码值的数据点将被散列到同一个桶中[14],每个哈希表都包含若干个桶。如图1所示，通过投影和量化操作，数据点p被索引到哈希表中的某一个桶内，每个哈希表都包含了数据库中所有的点。使用多个哈希表的目的是为了增加找到真正近邻的概率，消除哈希桶边界的影响。余下的操作就是如何实现哈希表的压缩存储，同时尽量减少不相似的数据点发生冲突，详细的描述可以查阅文献[15]。

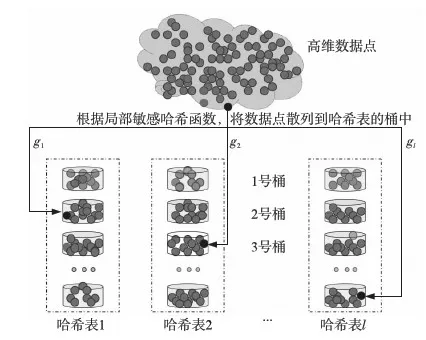
Figure 1 Indexing data in LSH algorithm[16]图1 LSH算法索引数据的过程[16]

在查询阶段，查询数据点q以同样的方式被散列到l个哈希表中。在每个哈希表中和查询点q位于同一个桶内的数据点可能是近邻而被返回，所有的返回数据点构成一个短列表(short-list)，short-list包含的数据量远远小于数据库中所有元素的数量，顺序搜索short-list中的数据点，得到查询数据的近邻。

3.2 算法分析

LSH算法[4]没有考虑数据的分布结构，哈希函数是基于p-稳态分布随机生成的，所以为了提高算法的性能，就必须提高哈希表的数量l和第二级哈希函数的长度k。参数l越大，找到近邻的可能性就越大，但是查询时间会变长，内存的使用量也会增加。参数k越大，二级哈希函数的值越能准确地反映公式(1)中相似度的值，当然如果k取较小的值，散列操作会变得更快。

4 LSH算法的改进

空间复杂度可以用哈希表的个数来表示，或者用内存总的使用情况来衡量[8]。改进后的算法I-LSH可以使用较少的哈希表就能达到较好的查询效果，性能和顺序搜索相当，将I-LSH用于副本图像检索任务。在不降低或不显著降低算法性能的前提下，减少哈希表的数量能有效地降低算法的空间复杂度。设计合理的哈希函数能实现这个目标，实质就是确定哈希函数的投影方向ai。

借鉴模式识别中主成份分析PCA(Principal Component Analysis)的思想，将哈希函数投影方向的生成过程归纳如下：

(1)从数据库中均匀、随机选出m个数据点，构造为集合{p1,p2,…,pm}，计算该集合的协方差矩阵:

(4)

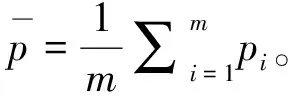
(2) 排序该协方差矩阵∑的特征值，对应的特征向量为v1,v2,…,vn。

新的哈希函数增加了对数据的区分性，能使数据点更均匀地分布到哈希桶中，落入同一个桶中的数据点的相似性大大增加了。在计算能力容许的前提下，应选择较大的m值，这样得到的哈希函数会更适合索引当前数据集。

5 实验仿真与结果

5.1 数据集的建立

实验采用了文献[17]提供的一个图像评价集，它包括两个真实图像集和一个人为编辑过的图像集(Dark Knight, The Lord of The Rings, Flickr)。在Flickr数据集中，通过12种不同的方法编辑每一幅原始图像得到12幅近似图像，这12种编辑方法是图像模糊、亮度变化、存储格式改变、颜色变化、颜色增强、对比度变化、压缩、剪切、在图像中增加标识(Adding Logo)、分辨率改变、缩放和以上多种方法的联合使用。文献[16]给出了更详细的描述。同时又搜集了若干的网络图像，通过随机采样构建大小不同的“迷惑图像”集混合到评价集中，实验分别在六个规模不同的数据集上进行，使用40维的Gist表示每一幅图像，最小的数据集包含四千幅图像，最大的数据集包含七万幅图像。

5.2 评价测度

图像检索任务的评价测度很多，常见的评价测度包括查准率Precision、查全率Recall、均值平均精度mAP(mean Average Precision)等。给定一幅查询图像，系统返回的结果可以被标记为如下四种类型：正确的正样本TP(True Positive)、错误的正样本FP(False Positive)、正确的负样本TN(True Negative)、错误的负样本FN(Flase Negative)。TP的含义是系统将返回结果判定为相关图像，实际也如此；FP的含义是系统将返回结果判定为相关图像，实际上返回结果与查询图像却是不相关的；TN的含义是系统将返回结果判定为不相关的图像，实际上返回结果与查询图像也确实是不相关的；FN的含义是系统将返回结果判定为不相关图像，实际上返回结果与查询图像却是相关的。Precision和Recall的计算公式定义为：

(5)

其中符号#表示样本的数量，#TP与#FN的和是数据库中所有相关样本的数量。如果系统对查询结果做了排序，然后从第一幅图像开始依次对这个排序表进行检查，可以计算出若干组对应的Precision和Recall的值，进而绘制查准率/查全率曲线(P-R curve)。

Figure 3 Comparison of query results exhaustive search, LSH and I-LSH图3 穷尽搜索、LSH和I-LSH方法的查询结果比较

作为图像检索的评价测度，mAP已经被广泛使用[13,18]。输入一幅查询图像，可以计算和绘制它的精度-召回率曲线(Precision-Recall Curve)，精度-召回率曲线下的面积值被定义为平均精度AP(Average Precision)。给定一组查询，可以获得一组平均精度，它们的平均值就被称为mAP。

5.3 实验结果和分析

实验中对short-list的排序使用了2范数距离测度。图2给出了顺序搜索算法、I-LSH算法和LSH算法[4]的比较结果，为了比较算法的性能，LSH算法和I-LSH参数取值均为l=5,k=3,w=0.1。 可以看出,在空间复杂度相同的情况下，改进后的算法I-LSH的性能比标准LSH要好很多，而且十分接近穷尽搜索的结果。穷尽搜索是LSH算法的极限情况(一个哈希表只包含一个哈希桶)，所以穷尽搜索的结果可以被看作理想的参照基准。由图2可以看到，当l的值较低时，LSH算法还表现出随意性。在图3中第1行是随机选择的一幅查询图像，第2行是穷尽搜算法返回的相关图像，第3行是LSH算法返回的相关图像，第4行是I-LSH算法返回的相关图像。图4～图6是三种算法对应的查准率-查全率曲线图。

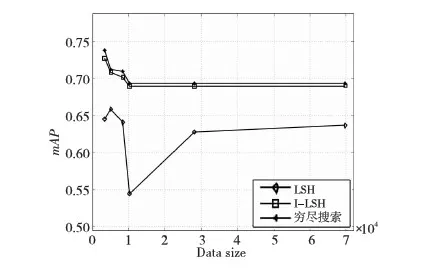
Figure 2 Comparison of mAP among exhaustive search, LSH and I-LSH图2 穷尽搜索、LSH和I-LSH方法的mAP性能比较

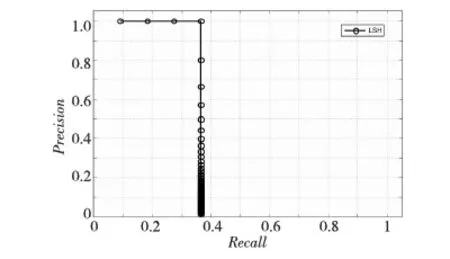
Figure 4 Curve of Precision-Recall of LSH图4 LSH算法的查准率-查全率曲线图

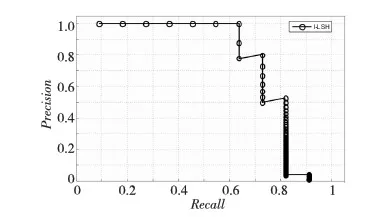
Figure 5 Curve of Precision-Recall of I-LSH图5 I-LSH算法的查准率-查全率曲线图

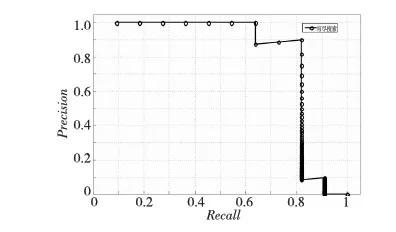
Figure 6 Curve of Precision-Recall of exhaustive search图6 穷尽搜索算法的查准率-查全率曲线图

6 结束语

本文改进了LSH算法，该算法不需要有标记的样本，仅仅利用数据的分布信息构造投影方向，使生成的哈希函数更适合目标数据库。实验结果表明，改进的LSH算法有效地降低了内存的使用量，性能也相当接近穷尽搜索算法。

[1] Lowe D G. Distinctive image features from scale invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2):91-110.

[2] Jagadish H V, Ooi Beng Chin, Tan Kian-Lee, et al. iDistance:An adaptive B+-tree based indexing method for nearest neighbor search[J]. ACM Transactions on Data Base Systems, 2005, 30(2):364-397.

[3] Guttman A. R-Trees：A dynamic index structure for spatial searching[C]∥Proc of ACM SIGMOD International Conference on Management of Data, 1984:47-57.

[4] Datar M, Immorlica N, Indyk P. Locality sensitive hashing scheme based onp-stable distributions[C]∥Proc of Symposium on Computational Geometry, 2004:253-262.

[5] He Zhou-can, Wang Qing, Yang Heng. An extended local sensitivity Hash algorithm for feature correspondence and image matching[J]. Journal of Sichuan University, 2010, 47(2):269-274.(in Chinese)

[6] Kullis B, Grauman K. Kernelized locality sensitive Hashing for scalable image search[C]∥Proc of ICCV, 2009:2130-2137.

[7] Ryynanen M, Klapur A. Query by humming of midi and audio using locality sensitive hashing[C]∥Proc of ICASSP, 2008:1.

[8] Cai Heng, Li Zhou-jun, Sun Jian, et al. Fast image retrieval based on LSH indexing[J]. Computer Science， 2009, 36 (8):201-204.(in Chinese)

[9] Lu Yan-sheng, Rao Qi. A self-tuning method of LSH index[J]. Journal of Huazhong University of Science and Technology, 2006, 34(11):38-40.(in Chinese)

[10] Yang Heng, Wang Qing, He Zhou-can. Multiple randomized sub-vectors quantization hashing for high-dimensional image feature matching[J]. Journal of Computer-Aided Design & Computer Graphics, 2010, 22(3):409-502.(in Chinese)

[11] Cao Y D, Zhang H G, Guo J. Matching image with multiple local features[C]∥Proc of ICPR,2010:519-522.

[12] Oliva A,Torralba A.Modeling the shape of the scene:A holistic representation of the spatial envelope[J]. International Journal of Computer Vision, 2001, 42(3)：145-175.

[13] Douze M, Jegou H, Sandhawalia H. Evaluation of GIST descriptors for web-scale image search[C]∥Proc of CIVR, 2009,DOI:10.1111511646396.1646421.

[14] Ma Ru-lin, Jiang Hua, Zhang Qing-xia. An improved fast searching method of hash table[J]. Computer Engineering & Science, 2008, 30(9)：66-68.(in Chinese)

[15] Shakhnarovich G,Darrell T,Indyk P.Nearest-neighbor methods in learning and vision:Theory and practice[M]. Cambridge:MIT Press, 2006.

[16] Cao Yu-dong, Liu Fu-ying, Cai Xi-biao. Research on high dimension image data indexing technology based on locality sensitive hashing algorithm[J]. Journal of Liaoning University of Technology, 2013, 33(1)：1-4.(in Chinese)

[17] Kim H, Chang H W, Lee J. BASIL:Effective near-duplicate image detection using gene sequence alignment[C]∥Proc of ECIR, 2010:229-240.

[18] Philbin J, Chum O, Isard M, et al. Object retrieval with large vocabularies and fast spatial matching[C]∥Proc of CVPR, 2007,DOI:10.1109/CVPR.2007.383172.

附中文参考文献：

[5] 何周灿, 王庆, 杨恒. 一种面向快速图像匹配的扩展LSH算法[J]. 四川大学学报, 2010, 47(2):269-274.

[8] 蔡衡, 李舟军, 孙健，等. 基于LSH的中文文本快速检索[J]. 计算机科学, 2009, 36 (8):201-204.

[9] 卢炎生, 饶祺. 一种LSH 索引的自动参数调整方法[J]. 华中科技大学学报, 2006, 34(11):38-40.

[10] 杨恒, 王庆, 何周灿. 面向高维图像特征匹配的多次随机子向量量化哈希算法[J]. 计算机辅助设计与图形学学报, 2010, 22(3):409-502.

[14] 马如林, 蒋华, 张庆霞. 一种哈希表快速查找的改进方法[J]. 计算机工程与科学, 2008, 30(9):66-68.

[16] 曹玉东, 刘福英, 蔡希彪. 基于局部敏感哈希算法的图像高维数据索引技术的研究[J]. 辽宁工业大学学报, 2013, 33(1)：1-4.