基于观察学习的机场噪声监测点关联预测研究*

陈 曦，王建东，陈海燕

(南京航空航天大学计算机科学与技术学院，江苏 南京 210016)

1 引言

大规模的机场建设使机场噪声问题日益严重。机场噪声的产生因素非常复杂，涉及航班调度、机场建筑布局、飞行程序、发动机功率、飞行速度以及气温、湿度、气压等环境因素。噪声是不可避免的，但可以在可控的因素上人为地降低机场噪声的大小，以减少对周围环境的影响[1]。针对这个问题，现有方法是通过在噪声波及范围内设置噪声监测点来及时捕获噪声数据，为噪声防治提供决策依据。 然而，由于监测点设备的损坏和老化时有发生，导致监测点失效或数据采集错误，这时就无法得知该区域噪声的真实情况。因此，如何在设备发生故障时准确预测失效监测点区域的噪声成为一个值得深入研究的问题。

机场的噪声监测点设备通常比较昂贵，且维护成本高[2]。在传感器布置上，为了防止单一节点失效而引发的监测数据异常，一般是采用硬件冗余的方式，即在各个监测节点上，布置多个传感器。这样势必会造成一系列巨大的硬件浪费，特别在像机场噪声监测这种大规模监测活动中。

通过对历史实测噪声数据的分析发现：监测点之间存在一定的关联性，如，相邻两个监测点的噪声数据相近、相邻区域内的噪声数据呈相似的变化趋势等。因此，通过选取与失效监测点相关性最高的几个监测点，利用这些点的噪声值学习一种基于监测点关联的预测回归模型，就可以对失效的监测点进行噪声值估计。目前，关于基于噪声监测点的关联预测问题的研究在学术界还很少见。鉴于BP神经网络在对非线性回归预测问题上的良好表现，及其在机场噪声预测上取得的良好效果[3,4]，本文提出了一种基于观察学习的机场噪声监测点关联预测模型，针对BP神经网络在小样本数据集上的欠拟合问题，以及受初始网络节点权重影响较大的问题，建立了BP神经网络集成，并提出一种基于学习成果优异度加权的观察学习算法，提升整个预测模型的泛化能力和预测精度。最后用基于机场噪声实测数据的实验来检验该模型的有效性。

2 观察学习算法(OLA)原理

在神经网络集成中，数据集的大小直接影响了最后的训练效果。对于复杂的回归问题，过小的训练样本集有可能会导致神经网络发生欠拟合。而在许多情况下，受制于客观因素，增加训练样本是困难的，甚至无法做到。因此，如果大多数神经网络发生欠拟合状况，那么势必整个集成模型也会受到拖累，无法得到较好的回归效果。

观察学习算法OLA(Observational Learning Algorithm)是1999年由Jang M[5,6]提出的一种应用于人工神经网络的集成学习技术。它的提出正是为了解决上述问题。其学习的方式为在训练的过程中，不断生成虚拟数据来扩充训练集，同时集成模型中各个神经网络互相学习其他神经网络的成果来提高整个集成模型的泛化能力。

其思路来源于班杜拉的社会学习理论。OLA认为，对于集成的神经网络，如果一个学习器从训练数据集上获得的直接经验无法训练出较好的结果，那么可以通过观察其他学习器是如何做的并且学习它们来获得间接经验。在起始阶段，受制于训练样本集过小，单个学习器对任务的认知较匮乏，那它们的集成模型的预测精度也会较低。通过按照训练样本分布规律生成虚拟数据集，将其扩充到训练数据集中，可在一定程度上解决训练样本集过小的问题，避免欠拟合。随着观察和训练的过程不断重复，单个学习器将逐渐对任务有充分的学习，并且各个学习器之间互相学习、提高，最后，提升了集成模型的泛化能力，从而在一定程度上解决了集成中弱学习器影响模型整体回归效果的问题[7]。

OLA的模型训练过程如图1所示，包括两个阶段：训练阶段(T-step阶段)和观察阶段(O-step阶段)。在T-step阶段，在数据集上进行多个学习器的训练；在O-step阶段，观察其他学习器的结果，产生用于各个学习器的虚拟数据集。这两个阶段交替进行，对集成模型进行训练。对于集成模型中各个神经网络i的虚拟数据集的输入，为其初始训练数据集加上高斯白噪声产生，其输出为利用虚拟数据集输入在-i集成上产生(集成模型中，去除神经网络i的决策输出)。

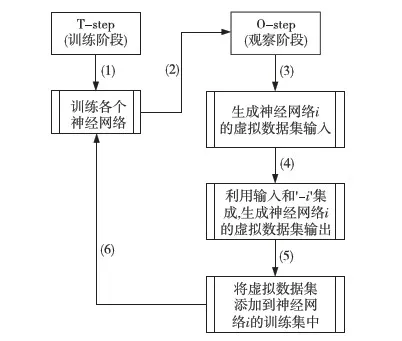
Figure 1 OLA working mechanism图1 OLA运行机制

在Jang M的工作基础上，学者们对OLA做了进一步的研究，Yu Fan等人[8]将OLA扩展到异构集成模型上，并证明其能较大程度地提高模型的泛化能力；Wong P M等人[9]将OLA应用到储层的多渗透率预测，取得良好的应用效益，并将模型扩展到多预测输出问题上；Shin H[10]在OLA中引入聚类思想，将数据集划分给不同网络训练并进行模块化的集成，提出了MOLA模型； Lu Zong-lei等人[11]将OLA扩展到用于预测概率分布。然而，前人的研究侧重OLA的应用和模型的集成，对其中权值和参数的设置未做详细研究。本文一方面尝试将OLA方法用于机场噪声监测点的关联预测，另一方面研究如何设置权值和参数来提高OLA的性能。

3 关联监测点的筛选

关联监测点的选取方式有很多，最直观的方式是根据监测点之间距离直接选取，监测点之间的距离越近，它们监测到的噪声大小应该越接近，其关联度越高。这种方法适用于监测点布局比较密集的情况。对于监测点布局较为稀疏，或者有建筑物干扰的情况，选取距离最近点并不完全适用，目前机场噪声监测点的布局正是这种情况。因此，比较可靠的做法是根据历史监测数据来计算监测点之间的关联度，进而选取到关联度较高的监测点。这里，使用常见的皮尔逊相关系数(Correlation coefficient)作为监测点之间关联度的衡量标准，其计算方法如式(1)所示。

(1)

假设除失效监测点x外的监测点集合为P={p1,p2,…,pr}，则关于x的关联度集合为ρxy={ρx1,ρx2,…,ρxr}。通过设置关联度阈值ε，当ρxy≥ε时，可选入监测点y的关联监测点集合Q={q1,q2,…,qr′|r′≤r}。在此集合上，构造训练和测试模型所需的数据集。

使用相关系数来衡量监测点之间关联度的优势在于：不但考虑监测点之间的噪声值是否相近，同时还考虑到监测点之间噪声值的变化趋势是否相类似。这样，即便在监测点布局较为稀疏或建筑物较多的情况下，也能选择到合适的关联监测点。关联监测点的筛选同时还起到了降维的作用，剔除了对关联预测贡献不大的监测点。

4 基于观察学习的噪声监测点关联预测模型的建立

4.1 数据集的准备和BP神经网络的构造

BP神经网络结构为三层[12，13]。由于是利用关联监测点的噪声值来预测失效监测点的噪声值，因此在模型中，输入层的神经元节点数等于r′，输出层的节点个数为1，隐藏层的节点个数为2×r′。构造出含有L个BP神经网络的集成模型F=[f1,f2,…,fL]。采用Bootstrap在训练集D上产生给各个神经网络fi的训练集DF=[D1,D2,…,DL]。

4.2 MSE-OLA

为了更好地发挥观察学习的优势，以及提升模型在小样本条件下的泛化能力，本文在OLA的框架下，提出一种基于学习成果优异度加权的观察学习算法MSE-OLA(Mean Squared Error OLA)。

算法MSE-OLA

输入：初始BP神经网络集成模型F=[f1,f2,…,fL]，初始训练数据集DF=[D1,D2,…,DL]，模型最大训练次数G。

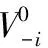
步骤2For(t=0;t≤G;t++)

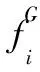
为了在本模型上得到更好的训练效果，该算法从三个方面进行权值和参数的设置。

4.2.1 高斯白噪声的方差

虚拟数据集的生成是观察学习的重要步骤，直接影响子学习器的重训练效果。OLA的训练结果对于高斯白噪声的方差不太敏感，只要不是极端，都能有较好的训练效果，因此其方差设置通常是按照经验来设置的[6]。对于较小的训练集来说，方差会对模型的重训练效果产生影响。本文将高斯白噪声设置为均值0，方差为1/n，其中n为原始训练数据集的大小。这样，当数据集较小时，方差较大，能产生具有多样性的数据，避免过拟合；当数据集较大时，方差较小，数据的多样性降低，可以在一定程度上控制拟合偏差。

运用于BP神经网络i的虚拟数据集输入可表示为：

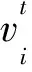
zk～N(0,1/n),k=1,…,n}

(2)

其中，zk为满足分布为均值0、方差1/n的高斯白噪声向量，xk属于神经网络i的初始训练集Di。

(3)

(4)

(5)

矩阵每一行表示其他神经网络参与第i个神经网络的-i集成的权值。

这种基于学习成果优异度加权方法从社会学习理论的角度可以理解为：学习者对一项任务的完成能力是有限的，他们在观察其他人是如何完成任务时，总是会向能力较强的人多学习一些，而向能力较弱的人少学习一些甚至不学习，即有侧重地学习。

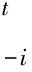
(6)

至此，其运用于下一个训练阶段的虚拟数据集则为：

(7)

4.2.3 集成模型中各个网络的决策输出权值

(8)

其中，fi为模型中的各个BP神经网络，αi为其在决策输出时的权值。在OLA中，αi一般采用均值的方式，即αi=1/L。

在经过OLA训练后，模型中的各个神经网络都能够得到充分的训练，并且提升预测精度。不过，在预测的能力上参差不齐的现象还是无法避免。 因此，为了能够使集成模型具有更好的预测效果，本文同样也使用“基于学习成果优异度的加权”，令各个神经网络在测试集上的表现能力作为各自参与模型决策输出的权重。因此，定义其计算方法如式(9)所示：

(9)

其中，σi由式(3)计算得出。

5 实验与评价

已有数据为国内某国际机场2010年至2011年16个监测点日均噪声数据，从全部16个监测点中选取一个点作为需要进行预测的失效监测点，其余点作为候选关联监测点。数据集包含了两年监测的730条数据，每条数据为这16个监测点在同一天的日均噪声数据值，随机选取其中的200条作为测试数据集，另外530条作为原始训练数据集。

5.1 关联监测点的筛选

将每天的日均噪声数据值作为监测点的属性，则每个监测点有530个属性，利用皮尔逊相关系数计算出失效监测点与其他15个监测点的关联度，计算结果如表1所示。

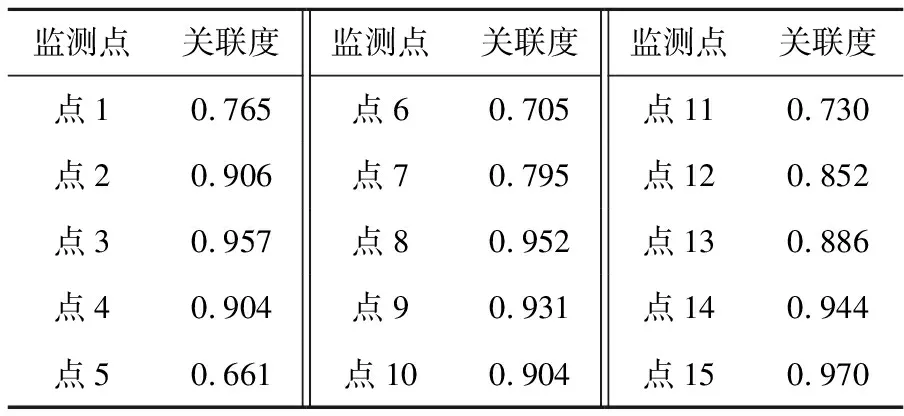
Table 1 Correlation between abnormal node and normal nodes

从表1中可知，关联度大于0.9的点占了一大半，为了得到较好的训练效果，本文只选择关联度大于0.9的8个监测点来构造BP神经网络集成模型。

5.2 数据集的构造和BP神经网络集成模型的构造

经过筛选出来的关联监测点有8个，所以训练数据集的输入属性维度为8，输出属性维度为1。由于输入维度和数据集较小，因此本实验采用五个BP神经网络进行集成。

5.3 训练

首先，采用Bootstrapping算法在原始数据集上生成五组训练集；进而，训练得到五个BP神经网络；根据各神经网络在测试集上的MSE计算它们在观察学习阶段对产生虚拟数据集输出的权值。

接着，把原始数据集中的每个数据加上高斯白噪声生成虚拟输入数据，其中高斯白噪声的均值为0，方差为1/530。表2显示了对模型进行21次观察学习训练(一次原始训练集训练和20次虚拟数据集训练)时，每个训练阶段各个BP神经网络以及集成后产生的MSE。

从表2中可以看出，在没有加入虚拟数据集进行重训练时，各神经网络的泛化能力不强，集成模型的预测精度也不高；当循环重训练开始时，各神经网络的学习效果在不断地发生波动，MSE的总体呈现下降的趋势，集成模型的预测精度也在提高，MSE下降得很快；随着重训练次数的增多，集成模型预测精度趋于稳定。

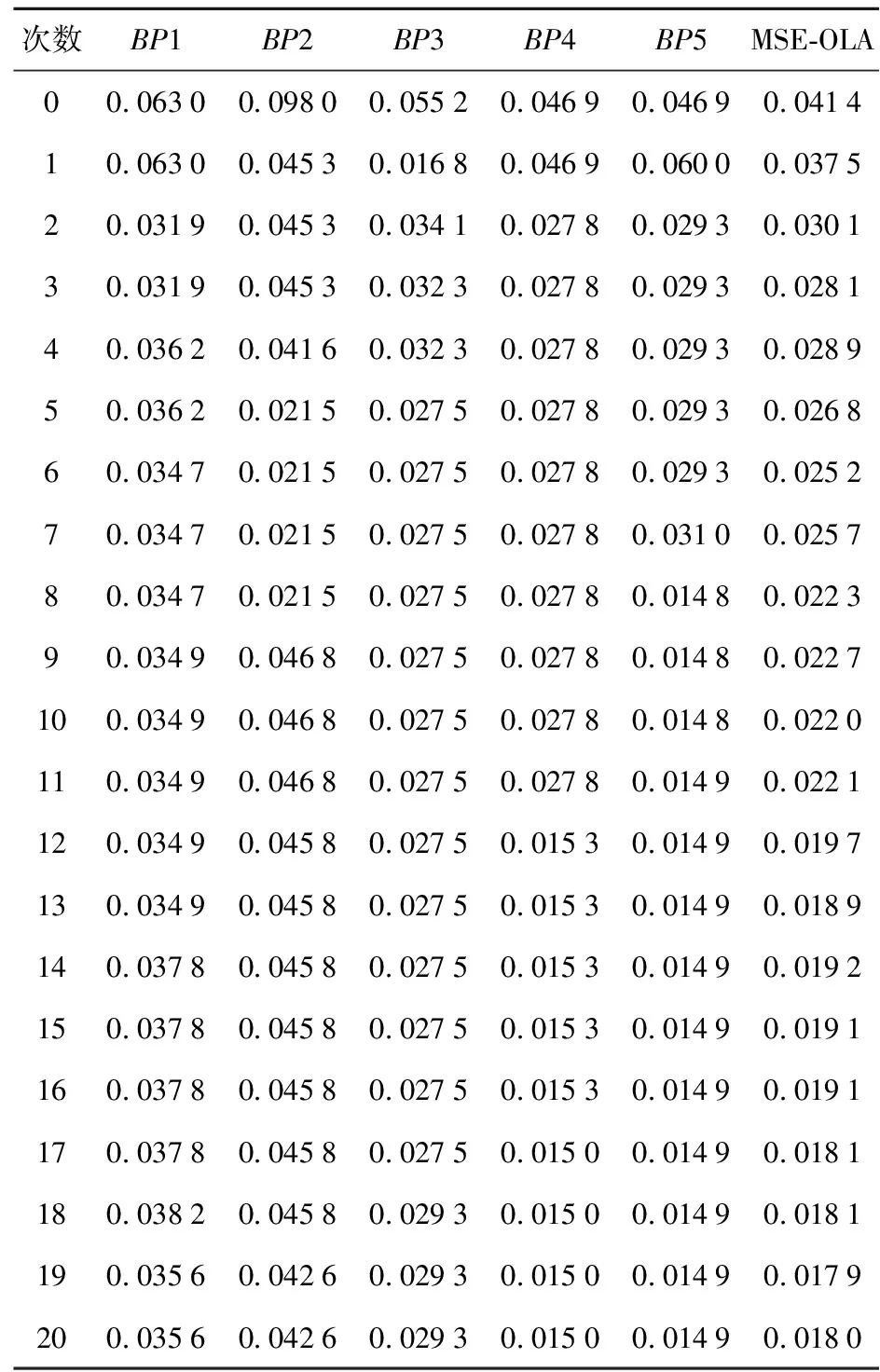
Table 2 Trend of MSE for MSE-OLA

表3显示了同样条件下普通取均值加权的观察学习算法各训练阶段的MSE。

从表3中可以看出，取均值加权的OLA对集成模型有很大的优化，使集成模型的预测精度得到提高，但多个神经网络的MSE波动起伏很大，总的集成效果不如MSE-OLA。

BP神经网络集成模型在两种算法的优化下，训练过程的MSE变化趋势图如图2所示。

Figure 2 MSE for two OLA algorithms图2 两种OLA的MSE变化趋势

次数BP1BP2BP3BP4BP5AverageOLA00.06300.09800.05520.04690.04690.045410.05740.01290.05220.07100.07010.045320.05740.01340.03470.07100.07010.042130.04730.01390.03470.08850.04360.038740.04730.01560.02890.08850.04360.039050.04730.01560.02890.05760.04500.035060.04730.01560.02890.05760.04500.035070.03080.01560.02890.05760.04500.031980.02930.06480.02890.05760.04500.032990.02930.06480.02890.05760.04500.0329100.02930.06480.02890.05760.04500.0329110.02930.06480.02890.05610.09810.0389120.02930.01930.02890.05610.09050.0373130.02930.01930.02890.05610.09050.0373140.02930.01930.02890.05610.09590.0377150.02580.01930.02890.05240.09590.0365160.02580.01930.02890.05240.05590.0316170.02580.01930.02890.05240.05590.0316180.02580.01930.02830.05240.05590.0310190.02580.01930.02830.04990.05590.0307200.02580.01930.03210.04990.05590.0313

从图2中可看出，MSE-OLA相比取均值加权的OLA，重训练的效率得到提升，稳定性也增加了；同时，MSE下降的速率也提升了，这说明MSE-OLA相比于取均值加权的OLA能够在最少的重训练次数下较快地达到较好的训练效果，加速了模型的优化。

5.4 预测结果

经过上面的步骤得到了基于观察学习的机场噪声监测点关联预测模型，该模型在测试数据集上的预测结果如图3和图4所示。

Figure 3 Comparison between predicted outputs and expected outputs图3 预测输出与期望输出对比结果

Figure 4 Percentage of prediction error图4 预测误差百分比

从图3和图4可以看出，基于观察学习的噪声监测点关联预测模型，在测试集上的预测误差百分比控制在[-0.01,0.015]，因此该模型在预测失效点的日均噪声值时，预测结果能达到理想的精度。

6 结束语

本文针对机场噪声监测点失效导致的噪声采集数据错误问题，在不借助硬件的条件下，尝试以软件方式寻求解决方案。发现并分析了监测点之间的关联性，提出了利用监测点关联的对失效监测点日均噪声数据的预测模型。该模型使用相关系数来衡量和筛选关联度高的监测点，并利用BP神经网络集成作为学习器。为了解决小样本数据对模型训练的不充分以及提高模型的预测精度，提出一种基于学习成果优异度加权的观察学习集成算法对模型进行训练。实验中，用所提出模型对国内某机场的监测点噪声数据进行预测，实验结果表明，本文所提出模型具有较高的预测精度，且MSE-OLA较普通取均值的OLA能有效提升训练效率和稳定性。

本文的预测目标是失效监测点的日均噪声值，而对于时序性较强的实时噪声值预测将会是下一步研究的方向。另外，对于监测点间的关联性分析和度量方式，由于前人研究较少，所以有待做进一步的深入研究。

[1] Du Ji-tao. Research on airport noise prediction model and its application[D]. Nanjing:Nanjing University of Aeronautics and Astronautics,2011.(in Chinese)

[2] Ding Wen-ting. Research on location model of airport noise monitoring points[D]. Nanjing:Nanjing University of Aeronautics and Astronautics,2011.(in Chinese)

[3] Yang Y, Hinde C, Gillingwater D. Airport noise simulation using neural networks[C]∥Proc of the International Joint Conference on Neural Networks(IJCNN),2008:1917-1923.

[4] Du Ji-tao, Zhang Yu-ping, Xu Tao. Airport noise prediction model based on BP neural network[J]. Computer Engineering and Applications,2013,49(9):236-239.(in Chinese)

[5] Jang M, Cho S. Ensemble learning using observational learning theory[C]∥Proc of the International Joint Conference on Neural Networks(IJCNN),1999:1287-1292.

[6] Jang M, Cho S. Observational learning algorithm for an ensemble of neural networks[J]. Pattern Analysis & Applications, 2002, 5(2):154-167.

[7] Wang Shuo. Class imbalance learning[D]. Birmingham :University of Birmingham, 2009.

[8] Yu Fan, Yang Li-ying, Qin Zheng. Classifiers combination with observational learning[J]. International Journal of Computer Science and Network Security, 2006, 6(3A):53-56.

[9] Wong P M, Jang M, Cho S, et al. Multiple permeability predictions using an observational learning algorithm[J]. Computers & Geosciences, 2000, 26(8):907-913.

[10] Shin H, Lee H, Cho S. Observational learning with modular networks[C]∥Proc of the 2nd International Conference on Intelligent Data Engineering and Automated Learning(IDEAL), 2000:183-192.

[11] Lu Zong-lei, Xu Tao. A new method to predict probability distribution based on heterogeneous ensemble learning[J]. International Journal of Advancements in Computing Technology, 2012, 4(14):17-25.

[12] Hagiwara M. Removal of hidden units and weights for back propagation networks[C]∥Proc of the International Joint Conference on Neural Networks(IJCNN), 1993:351-354.

[13] Li Kai,Huang Hou-kuan.Study of a neural network ensemble algorithm for small data sets[J]. Journal of Computer Research and Development, 2006,43(7):1161-1166.(in Chinese)

附中文参考文献：

[1] 杜继涛.机场噪声预测模型及应用研究[D].南京:南京航空航天大学,2011.

[2] 丁文婷.机场噪声监测点分布模型研究[D].南京:南京航空航天大学,2011.

[4] 杜继涛,张育平,徐涛.一种BP神经网络机场噪声预测模型[J].计算机工程与应用,2013,49(9):236-239.

[13] 李凯,黄厚宽.小规模数据集的神经网络集成算法研究[J].计算机研究与发展,2006,43(7):1161-1166.