基于暂态可观性的向量测量单元配置方法

张启飞，苏小林，阎晓霞

（1.国网山西省电力公司检修公司，山西 太原 030006；2.山西大学，山西 太原 030013）

基于暂态可观性的向量测量单元配置方法

张启飞1，苏小林2，阎晓霞2

（1.国网山西省电力公司检修公司，山西 太原 030006；2.山西大学，山西 太原 030013）

指出向量测量单元布点问题需要在满足一定约束条件下同时优化2个相互冲突的指标，即配置向量测量单元的数目(或费用)最少和测量冗余度最高，提出了基于0—1规划法的模型对系统正常运行方式下稳态全可观的向量测量单元配置，与此同时，进一步研究在暂态情况下系统全可观的向量测量单元配置。利用N-1故障原则，给出了系统发生故障时向量测量单元进行配置时的约束条件，结合传统的配置指标，共同构成基于暂态可观的向量测量单元配置。通过对IEEE 30系统进行仿真，验证了向量测量单元配置方法的有效性。

向量测量单元配置；0—1规划法；N-1故障原则

0 引言

向量测量单元PMU（PhasorMeasurementUnit）具有GPS高精度授时的时标，可同步采集电力系统中各个节点的数据信息。在每个节点上都配置PMU，必然能实时监测整个系统的运行状态，但是，出于经济和技术上的考虑，这种配置方案很不现实，也很难实现。为此，电力工作者开展了最佳PMU配置OPP（Optimal PMU Placement）研究。

目前，已有研究者运用全局优化算法，以提高优化效率，并获得全局最优配置方案。其中，广泛运用的优化算法有遗传算法[1]、模拟退火法[2]、禁忌搜索法[3]。

另外，由于电力系统运行状态复杂，也提出了以某些特定目标为约束的PMU配置法。基于最佳状态估计为约束的PMU配置，是充分利用PMU和数据采集与监视控制系统各自的优势，以实现二者所提供的数据互为补充为目的[4-6]的配置方法。基于系统同调性的PMU配置，是在一个同调群内配置1台PMU以实现对整个同调机群内的监测，使得PMU配置数目最少，这种方法需要考虑故障发生概率[7]，需要考虑合理正确的分群方法[8]。

1 系统可观性评估原则

对系统可观性的评判有3个原则。原则1：与已配置PMU节点相邻的所有节点均可观测。原则2：对可观测的零注入节点来说，若与之相连的所有节点中，只有1个节点状态量未知，则该节点的状态也可得知。所谓零注入节点，就是指没有直接与发电机、带负荷的出线相连的节点。原则3：对状态量未知的零注入节点，若与之相连的所有节点均是可观测节点，则该零注入节点也可观测。

2 0—1规划法PMU配置

2.1 零注入节点简化

根据上节所述系统可观性评估原则，在配置PMU前，优先处理系统中所有的零注入节点，可最大程度简化系统的繁杂度。具体简化规则如下。

a）对于关联度为2的零注入节点，可以直接与其相连接的实心两节点之一合并。这是依据基尔霍夫电流定律以及欧姆定律得出的。

b）若零注入节点出线较多，在简化时应和与之相连的所有节点中关联度最小的那个节点合并。如果存在合并条件相同的情况，这就需要分别计算和每个节点合并下，PMU应配置的数目，然后进行验证是否满足全系统可观测性的要求，最后确定最终安装PMU的个数，选择最少的方案进行PMU的配置。

零注入节点简化方案如图1所示，其中，零注入节点用空心圆点表示。

图1 零注入节点简化方案

2.2 0—1规划法

0—1规划法是指在保证安装PMU的个数最少以及最佳安装位置的前提下，尽量达到最大的系统测量冗余度，而这些目标的实现必须要满足一定的约束条件。对具有n个节点的电力系统，就要求按照出线多少的顺序由大到小对各个节点排序，优先在出线多的节点处安装PMU，最终实现全系统可观。因此，PMU最优配置的目标函数见式（1）。

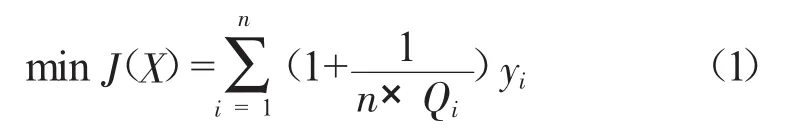
使得：

式中：Qi——与配置了PMU的节点i相关联的支路数之和；

A——支路—节点关联矩阵；

Y——Y=［y1，y2，…，yn］，若i节点配置PMU，yi则为1，否则yi为0；

I——单位阵。

2.3 基于暂态可观测的0—1规划法

由于某种扰动或事故发生时系统运行方式改变或者PMU装置发生测量、通讯故障时，系统将变得不可观测。所以，以系统完全可观测为目标的配置方案需要考虑各种故障条件下系统的可观性问题，即系统在受到故障后仍可保证系统结构完全可观测的PMU最优配置。

2.3.1 N-1故障集下的约束条件

在电力系统安全稳定评估中，通常采用N-1预想故障来评估电网的稳定特性。该准则规定，电力系统所有元件中，只有1个独立元件因故障而被迫退出运行后，应保证系统依然能稳定运行，不出现电压崩溃等事故。

对1个电力系统拓扑结构而言，在系统中的节点i和与它相邻节点之间的连接方式无非有两种情况：第一，2节点之间只有1条线路连接，用i1表示；第二，2节点之间至少有两条线路连接，用i≥2表示。

当发生单一故障后，情况一2节点将分离开来，相互独立；情况二2节点依然有联系。因此，在考虑了N-1故障情况下为保障系统完全可观，需要增加PMU的原则有以下几点。

a）节点i配置了PMU。

b）i1中2个节点都配置了PMU。

c）i≥2中有1个节点配置了PMU。

所以，用式（3）表示N-1故障集下的约束条件。

式中：X——X=［x1，x2，…，xn］；

A——支路—节点关联矩阵。在矩阵A中，若节点i处在系统端部或两节点之间有大于1条连接线，则其值取为2，若两节点之间只有1条连接线，则其值取为1，否则为0。

对于约束条件（4），要求不小于2是要保证关联度为1或者2节点之间只有1条线路连接的情况，也即对于处于系统端部且只有1条出线的节点必须安装PMU，才能保证此节点可观测。不大于等于4是保证多安装的PMU数量达到最小值。

2.3.2 基于暂态可观测的0—1规划法

将传统的0—1规划法加之故障集下的约束条件，可以使全系统不仅在稳态运行下，在故障时也能很好地达到系统全观测的目的，能时刻监视系统的运行状态。综合式（1）、式（2）、式（4），得到基于暂态可观测的0—1规划PMU优化配置算法式（5）。

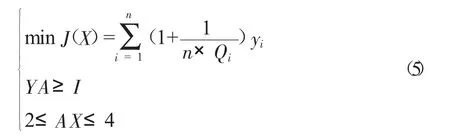
3 算例分析

为了验证该算法的有效性，在IEEE 30节点系统上进行了仿真分析与研究，分析了在稳态和暂态可观测的PMU配置情况。IEEE 30节点的网络拓扑结构如图2所示。

图2 30节点网络拓扑图

3.1 稳态全局可观测情况下的PMU配置

由网络拓扑结构可以看出，零注入节点分别为节点2、3和6。对这些节点进行简化处理。对节点2，根据简化规则，为了达到最少PMU配置，节点1与2合并是最优方案。对节点3，与之相连的节点4与23二者情况相同，应分别考虑这两种情况。对节点6，也同样需要考虑分别与节点5、7以及26合并的情况。所以，对该算例应考虑6种合并情况。

合并1：节点2和1合并；节点3和4合并；节点6和5合并；经计算共需要配置9个PMU达到系统全可观。

X=［0 1 0 0 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0 1 0 0 1 0 1 0 0 1 0］

合并2：节点2和1合并；节点3和4合并；节点6和26合并；经计算共需要配置10个PMU达到系统全可观。

X=［0 1 0 0 0 1 0 0 1 0 1 0 0 1 0 0 1 0 0 0 1 0 0 1 0 1 0 0 1 0］

合并3：将节点2和1合并；节点3和23合并；节点6和7合并；经计算共需要配置10个PMU达到系统全可观。

X=［0 1 0 0 1 0 0 0 1 0 1 0 0 1 0 0 1 0 0 0 1 0 0 1 0 1 0 0 1 0］

合并4：将节点2和1合并；节点3和23合并；节点6和5合并；经计算共需要配置10个 PMU达到系统全可观。

X=［0 1 0 0 0 1 0 0 1 0 1 0 0 1 0 0 1 0 0 0 1 0 0 1 0 1 0 0 1 0］

合并5：将节点2和1合并；节点3和4合并；节点6和7合并；经计算共需要配置11个PMU达到系统全可观。

X=［0 1 0 0 0 1 1 0 0 1 1 0 0 1 0 0 1 0 0 0 1 0 0 1 0 1 0 0 1 0］

合并6：将节点2和1合并；节点3和23合并；节点6和26合并，经计算共需要配置11个PMU达到系统全可观。

X=［0 1 1 0 0 1 0 0 1 0 1 0 0 1 0 0 1 0 0 0 1 0 0 1 0 1 0 0 1 0］

对上述6种合并情况进行分析，应用基尔霍夫电流定律以及欧姆定律来检验是否达到系统全可观。经分析计算，上述结果均能实现全系统的可观性。这6种方案以合并1安装PMU最省，共需要安装9个PMU，为基于稳态全系统可观的最佳PMU配置方案。

3.2 暂态全局可观测情况下的PMU布局

根据N-1故障集下的约束条件可列出如下一组约束方程

式中：X——X=［x1，x2，x3，…，x30］；

A——维数为30×30的对称方阵。

经计算，需要安装18个PMU达到系统全局可观测。

X=［1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 0 1 0 1］

所以，在受到干扰后需要安装18个PMU才能达到全局可观测。表1对本文所提方法与禁忌搜索法在配置PMU数目上进行了比较。

表1 IEEE 30系统PMU配置数目比较

4 结论

基于暂态可观测PMU优化配置算法既能保证在系统稳态全可观，又能保证在系统受扰后暂态行为的可观性。这种方法目标函数构造简单，算法易懂，计算量小，能够得到满意的优化结果。

参考文献：

［1］ Marin F J，Garcia-Lagos F，Joya Getal.Genetic algorithms for optimalplacementofphasormeasurementunit in electricalnetwork［J］.IEEE.Electronics Letters，2003，39（19）：1403-1405.

［2］ 杨明海，王成山.电力系统PMU优化配置方法综述［J］.电力系统及其自动化学报，2007，19（2）：86-92.

［3］ 陈年生，李腊元，董武世.基于禁忌搜索的QoS路由算法［J］.计算机工程与应用，2005，41（8）：134-136.

［4］ 毛安家，郭志忠.与SCADA互补的WAMS中PMU的配置及数据处理方法［J］.电网技术，2005，29（8）：71-74.

［5］ 郑相华，米增强，赵洪山，等.基于PMU的状态估计的研究［J］.继电器，2004，25（9）：16-19.

［6］ 王克英，穆钢，陈学允.计及PMU的状态估计精度分析及配置研究［J］.中国电机工程学报，2001，21（8）：29-33.

［7］ 许剑冰，薛禹胜，张启平，等.基于系统同调性的PMU最优布点［J］.电力系统自动化，2004，28（19）：22-26.

［8］ 张鹏飞，薛禹胜，张启平，等.基于PMU实测摇摆曲线的暂态稳定量化分析［J］.电力系统自动化，2004，28（20）：17-20.

PMU Configuration M ethod Based on Transient Observability

ZHANG Qifei1，SU Xiaolin2，YAN Xiaoxia2
（1.State Grid ShanxiM aintenance Com pany，Taiyuan，Shanxi 030006，China；2.Engineering College of Shanxi University，Taiyuan，Shanxi 030013，China）

PMU configuration needs to simultaneously optimize two conflicting indicators under some constraint conditions.One condition is that the number of PMU should be configured minimally and the other is that it should maintain the highestmeasurement redundancy.This paper presents the PMU configuration when the system operates steadily and fully observably based on 0—1 programmingmodel.At the same time,further study is done on the PMU configuration when system operates under transient state.By utilizing the N-1 faultprinciple,the constraint conditionswhen PMU needs to be configured when faults occur are given.Combining the traditional configuration index,a considerable PMU configuration based on transient state is formed.Through the simulation of IEEE 30 system,the proposedmethod isverified tobeeffective.

PMU configuration；0—1 programming plan；N-1 faultprinciple

TM991.2

A

1671-0320（2015）01-0005-04

2014-09-08，

2014-10-18

张启飞（1986），男，山西侯马人，2013年毕业于山西大学电力系统及其自动化专业，硕士，从事变电一次设备检修工作；

苏小林（1963），男，四川宜宾人，2009年毕业于清华大学电气工程专业，博士，教授，主要研究方向为电力系统运行与控制、智能电网；

阎晓霞（1963），女，山西平遥人，1984年毕业于太原工业学院电力系统及其自动化专业，副教授，主要研究方向为电力系统运行与控制。