“good”Boussinesq 方程的平均向量场方法
2015-07-10黄荣芳孙建强蒋朝龙
黄荣芳,孙建强,蒋朝龙
(海南大学 信息科学技术学院,海南 海口570228)
考虑如下的“good”Boussinesq 方程

方程(1)描述了非线性浅水波在2 个方向的传播,具有孤立子相互作用的互动机制[1-2].孤立波只存在有限范围的速度,孤子可以保持其形状和速度碰撞后小振幅孤子.然而对于大型振幅孤子,孤子可能发展成所谓的反孤立子.在周期或者零边界条件下,方程(1)有如下的守恒特性

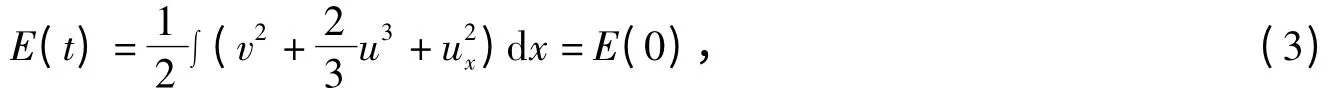
其中vx=ut.
对“good”Boussinesq 方程已经有大量的理论和计算方法研究:El-Zoheriry[3]构造了“good”Boussinesq方程的有限差分格式,并做了稳定性分析,保结构算法在求解“good”Boussinesq 方程具有显著的优势;Aydina 和Karaözen[4]构造了“good”Boussinesq 方程的辛和多辛LO-BATTO 格式;曾文平[5]和Huang[6]等构造了“good”Boussinesq 方程的多辛preissman 格式;胡伟鹏[7]等研究了广义Boussinesq 方程的多辛格式;蔡家祥[8]等构造了“good”Boussinesq 方程的局部保结构算法,并取得了很好的数值结果.然而,在数值求解时,能精确保持“good”Boussinesq 能量守恒特性的数值算法很少. 因此在数值求解时精确保持“good”Boussinesq 方程的能量对正确地模拟方程具有重要的意义.
最近在保结构算法领域内,Quispel[9]和Mclachlan[10]提出了精确地保持Hamilton 系统能量的平均向量场方法.平均向量场方法已被应用于KdV 方程,麦克斯韦方程等的求解[11].笔者利用平均向量场方法求解“good”Boussinesq 方程,并数值模拟孤立波在不同振幅下的演化行为和能量守恒特性.
1 平均向量场方法
对给定的Hamilton 系统


可知Hamilton 系统具有能量守恒的特性.
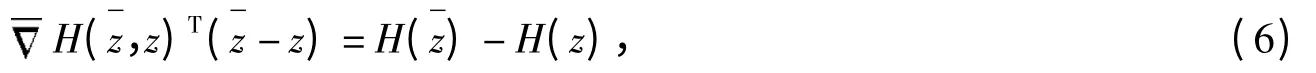

对式(4)在时间方向进行离散

其中 H(zn+1,zn)是Hamilton 系统能量函数的离散梯度为反对称矩阵.
定理1 离散梯度格式(8)保持Hamilton 系统能量守恒.
证明 由离散梯度的定义可知
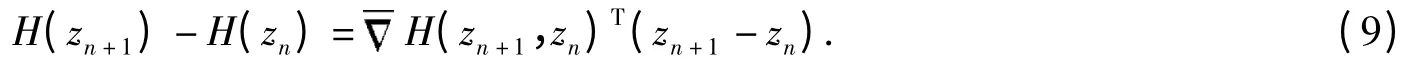
由式(8),可知
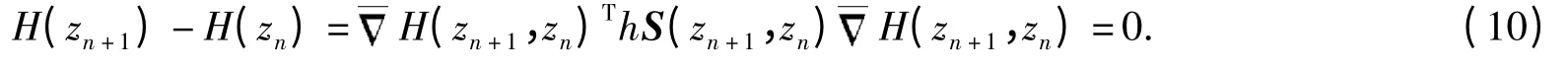
对于给定的Hamilton 系统,Quispel 和Mclachlan 给出了精确保Hamilton 系统能量守恒的二阶平均向量场方法
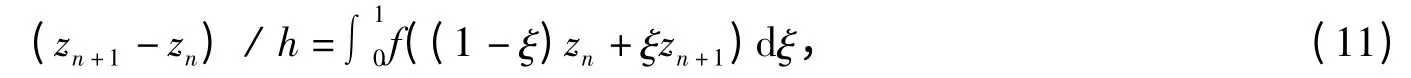
其中h 是时间步长[3].
定理2 平均向量场能够精确保持Hamilton 系统的离散能量守恒.
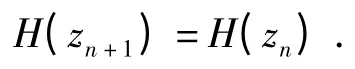
证明 方程(11)可以改写成
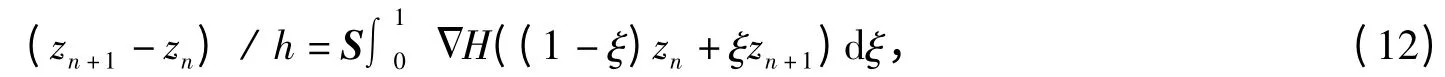

即
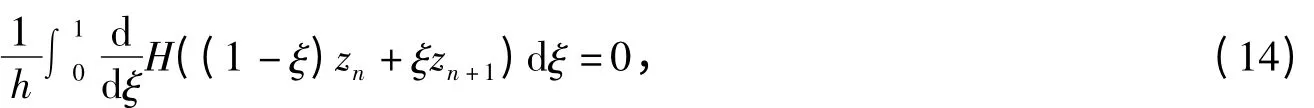
由微积分基本定理,可以得到(H(zn+1)-H(zn))/h=0.
因此,平均向量场方法可以在每个时间层上保持Hamilton 系统能量守恒.
2 “good”Boussinesq 方程的平均向量场格式
方程(1)可以写成无限维Hamilton 系统形式

其中z=(u,v)T,Hamilton 函数为

假设空间积分区间Ω=[a,b],空间长度L=a-b.将区间Ω=[a,b]分为N 等分,其中N 为正偶数,h=L/N 为空间步长.xj=a+hj,j=0,…,N-1 为空间配置点,uj和vj是对u(x,t)和v(x,t)在配置点xj的近似.
定义2
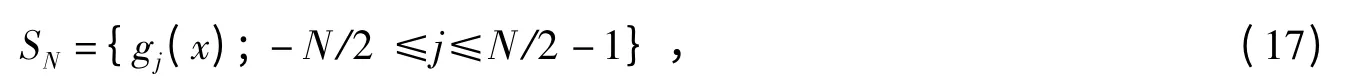
为插值空间,其中gj(x)可以被显示表示为

定义如下的插值算子IN,对于任意
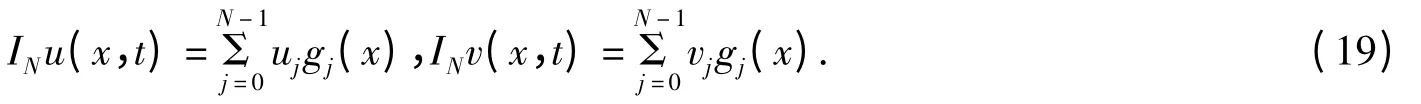
由于式(18)的正交性,可知

下面用uj来表示导数的值
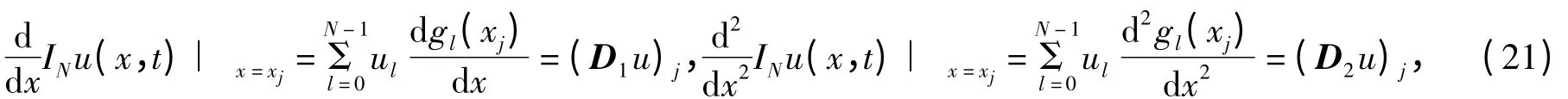
同理可得
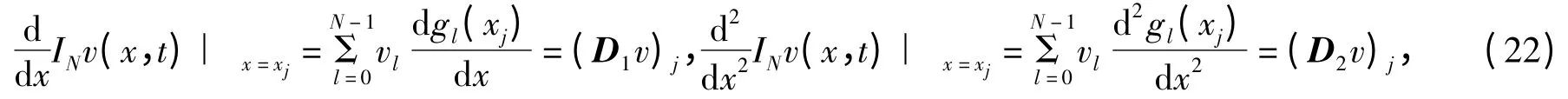
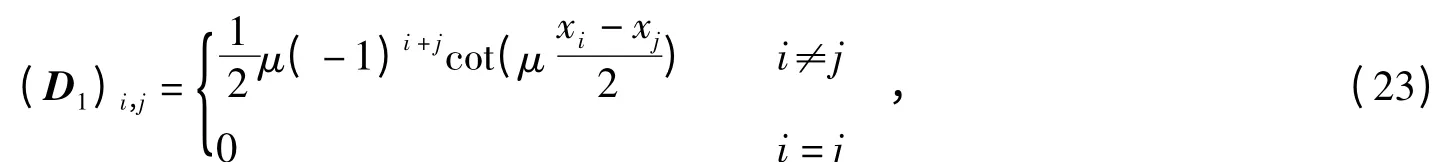
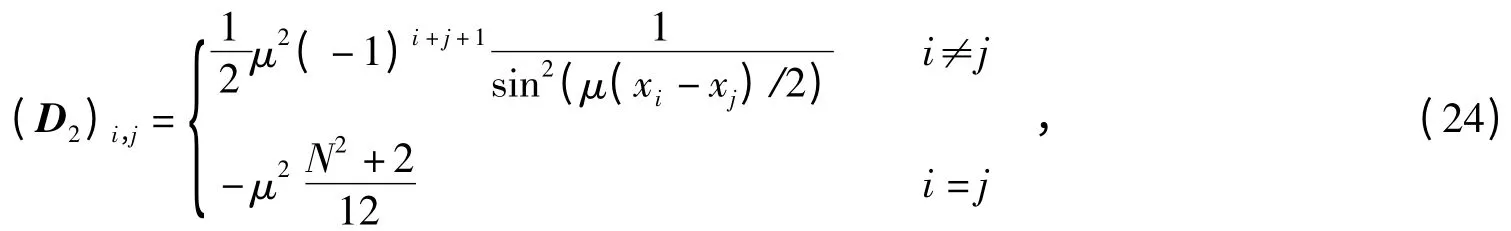
用D1近似∂x.在空间上,对式(15)进行谱离散,可以得到“good”Boussinesq 方程的Fourier 拟谱半离散形式

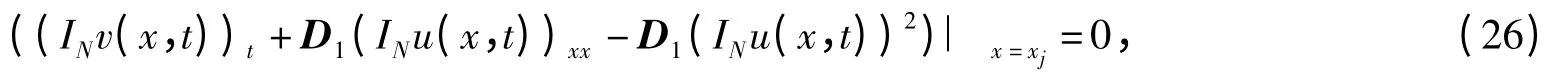
由式(21)和(22)可知式(25)和(26)等价于


其中A 是一阶谱微分矩阵D1和二阶谱微分矩阵D2的乘积,式(27)和(28)可以写成如下的Hamilton 形式

其中Z=(u,v)T,相应的离散Hamilton 能量函数为
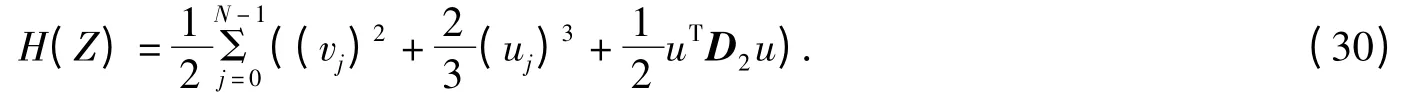
在时间方向上,将式(11)应用到式(29)得


对式(31)和(32)积分,可得到保“good”Boussinesq 方程离散能量的二阶平均向量场格式

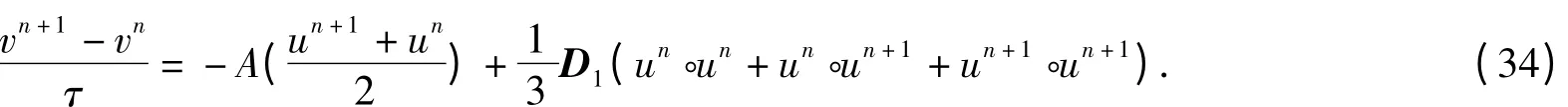
3 数值实验
为了验证上述理论分析的有效性,利用平均向量场格式数值模拟“good”Boussinesq 方程在不同振幅下的孤立波的演化行为.定义相对能量误差如下

其中H(Z0)是初始离散能量,H(Zn)是在t=nΔt 时的离散能量.
首先,考虑利用平均向量场格式模拟孤立子演化过程.初始条件为
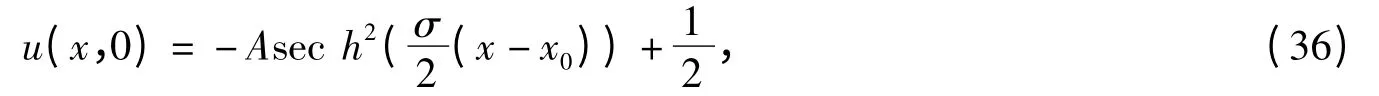

其中x0和σ 是实参数,A 是振幅,并且A=3σ2/2.
取-75≤x≤75,x0=0,τ =0.02,N =240 和周期边界条件,对孤立波在振幅A =1.48 时,进行数值模拟,如图1 和图2 所示.

图1 孤立波在A=1.48 时的演化行为
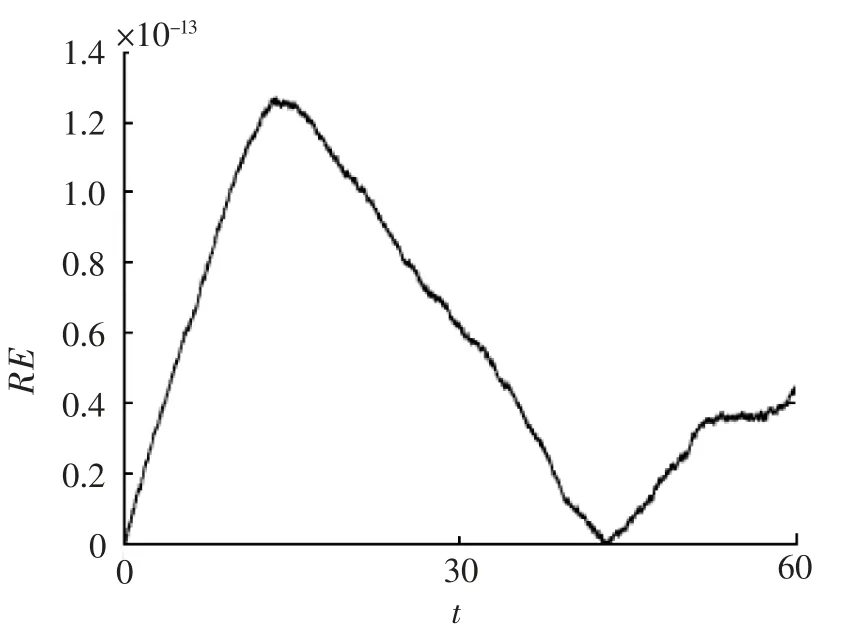
图2 在t [0,60]时的相对能量误差图
图1 为“good”Boussinesq 方程在振幅A =1.48 时,孤子波在t [0,60]时的演化行为.图1 表明孤立波演化过程中,分裂成2 列波,2 列波分别向相反的方向运动,这与文献[3]的结果是一致的.图2 表明孤立波演化过程中的相对能量误差图.从图2 可知,孤立波演化过程中相对能量误差可以到达10-13,系统能量守恒.由此可知,平均向量场格式不仅能很好地模拟孤立波的演化行为,并且能精确保持方程的能量.
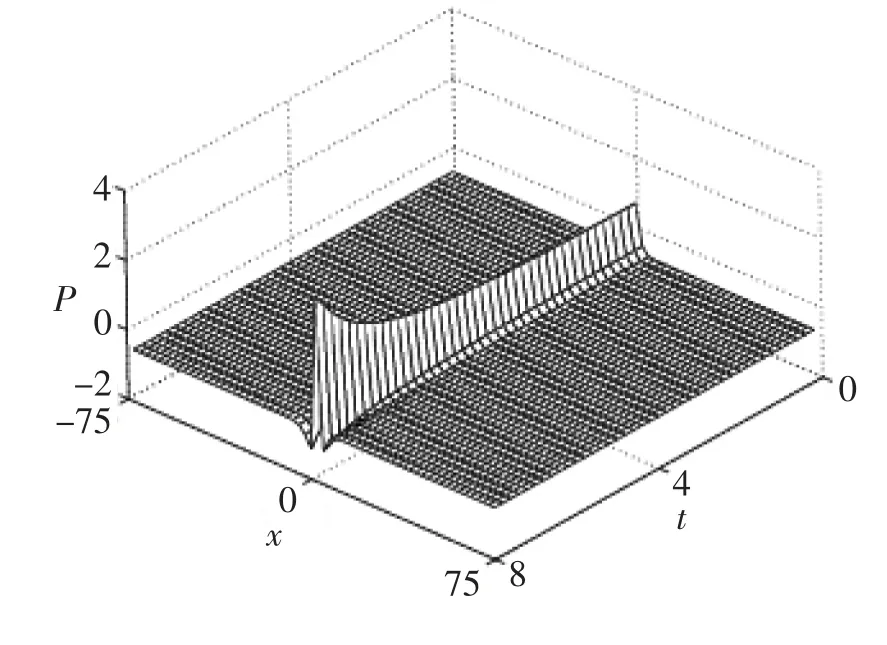
图3 孤立波在A=1.55 时的演化行为

图4 在t [0,8]时的相对能量误差图
图3 为“good”Boussinesq 方程在振幅A=1.55 时,孤立波在t [0,8]时的演化行为.从图3 中可以知道当在振幅A=1.55 时,孤立波演化一段时间之后出现了爆破(blows-up)现象.这与文献[3]的结果也是一致的. 图4 表明孤立波演化过程中方程相对能量误差图. 从图4 中可以看出孤立波演化过程中,即便出现了孤立波的爆破(blows-up)现象,但是方程的能量相对误差可以达到10-13,系统能量守恒.
4 小 结
本文构造了“good”Boussinesq 方程的平均向量场格式,利用平均向量场格式研究了孤立波在不同振幅条件下的演化行为. 数值结果表明,平均向量场格式不仅能很好地模拟孤立子波的演化行为,并且能精确保持方程能量. 平均向量场算法为数值模拟具有能量守恒的微分方程提供了新的选择.
[1]Manoranjan V S,Mitchell A R ,Morris J L L. Numerical solution of“good”Boussinesq equation[J]. SIMA J. Sci. Stat.Comput,1984,5(4):946 -957.
[2]Frutos DE J,Ortega T,Sanz-Serna J M. Pseudo-spectral method for the“good”Boussinesq equation[J]. Math. Comput,1991,57(195):109 -122.
[3]El-Zoheiry H. Numerical investigation for the solitary waves interaction of the“good”Boussinesq equation[J]. Appl. Num.Math,2003,45(2/3):161 -173.
[4]Aydin A ,Karasözen B.Symplectic and multi-symplectic Lobatto methods for the ”good”Boussinesq equation[J]. J. Math.Phy,2008,49(8):083509.
[5]Huang L Y,Zeng W P,Qin M Z. A new multi-symplectic scheme for nonlinear“good”Boussinesq equation[J]. J. Comput.Math.,2003,21(6):703 -714.
[6]曾文平,黄浪扬,秦孟兆. “good”Boussinesq 方程的多辛算法[J]. 应用数学和力学,2002 ,23(27):743 -748.
[7]胡伟鹏,邓子辰.广义Boussinesq 方程的多辛算法[J]. 应用数学和力学,2008,29(7):839 -845.
[8]Cai J X,Wang Y S. Local structure-preserving algorithms for the“good”Boussinesq equation[J]. J. Comput. Phy,2013(239):72 -89.
[9]Quispel G R W ,Mclachlan D I. A new class of energy-preserving numerical integration methods[J].J Phys. A:Math. Theor,2008,41(4):1 -7.
[10]Mclachlan D I,Quispel G R W,Robidoux N. Geometric integration using discrete gradients[J].Phil. Trans . Roy. Soc.A. 1999,357(1754);1 021 -1 045.
[11]Celledoni E,Grimm R I,Mclachlan D I,et al. Preserving energy resp. dissipation in numerical PDEs using the average vector field method[J]. J. Comput. Phys.,2012,231(20):6 770 -6 789.
