交通荷载作用下上覆硬壳层软土地基动力响应特征
2015-07-07曹海莹刘云飞任晓军李雨浓
曹海莹,刘云飞,任晓军,李雨浓
(1.燕山大学建筑工程与力学学院,河北秦皇岛 066004;2.河北工业大学土木工程学院,天津 300401;3.天津铁道职业技术学院,天津 300240)
交通荷载作用下上覆硬壳层软土地基动力响应特征
曹海莹1,刘云飞1,任晓军2,3,李雨浓1
(1.燕山大学建筑工程与力学学院,河北秦皇岛 066004;2.河北工业大学土木工程学院,天津 300401;3.天津铁道职业技术学院,天津 300240)
借助数值模拟软件FLAC3D的动力分析功能,编制了计算模型构建与求解的程序,对交通荷载作用下上覆硬壳层软土地基动力响应特征展开分析.交通荷载作用下产生的动应力在地基土中的传递规律表现出以下特征:不同埋深处,应力时程曲线波动出现短暂的滞后现象;应力水平的高低以及有无硬壳层对于动应力衰减速率影响较大,动应力衰减速率呈现非线性变化特征;动应力沿深度方向的衰减率较静应力明显迅速;上覆硬壳层的存在增大了动应力的影响扩散半径,且动应力在地基土中的扩散路径得以改善.
软土地基;硬壳层;交通荷载;数值模拟;动力响应
0 引言
随着高速公路、高速铁路等交通形式对地基的稳定与变形要求愈加严格[1],近年来,交通荷载作用下地基土的动力响应问题引起了研究人员的广泛关注[2].当交通工具的行驶速度接近或达到地基的表面波速时,地基将产生剧烈的地面振动,导致地基土塑性变形累积和内部微缺陷的扩展,很可能产生严重的工程危害.因此,积极开展交通荷载作用下的土体动力特性研究具有十分重要的意义.
硬壳层的强度高,结构性强、属中等压缩性、承载能力好,通常情况下,硬壳层的厚度达到一定数值后,其“硬壳层效应”便开始显现出来,在工程实际中就有被利用的价值[3].目前,针对上覆厚硬壳层软土地基进行动力响应分析仍鲜见报道,研究内容主要停滞在静态荷载阶段[4].
车辆荷载是交通运营期的主要动态荷载形式,求解车辆荷载引起的地基土动力响应,目前比较常用的方法有解析方法[5]和数值模拟方法[6].解析方法的理论解表达式相对比较复杂,求解难度大,以往的研究大多都只推导出积分解的形式[7].而数值模拟方法能避免繁琐的公式推导,解决许多解析方法所不能求解的复杂工程问题.本文通过构建数值模型,对交通荷载作用下的上覆硬壳层软土地基动力响应进行数值模拟计算,并依据计算结果对其动力响应特征展开分析.
1 交通荷载表达式
模拟交通荷载首先需要对车体模型进行简化,采用1/4车体模型模拟车辆竖向振动比较合理[8].
车辆在行驶时会产生垂直震动,路面在承受车辆重力荷载时还会承受由车辆本身震动引起的动载.其中,路面不平整是引起车辆震动的主要原因,而车辆本身的各种因素引起的震动相对于不平整度引起的震动是非常微小的[9].因此,采用充分考虑路面不平整因素的荷载表达式来表述交通荷载[10]:

2 数值模型构建
借助有限差分软件FLAC3D强大的动力分析功能,编制了计算模型构建与求解的程序.下面对程序编制中的关键步骤进行简要介绍.
为了更为清晰地研究车辆荷载产生的动应力在地基土中的传播规律,车辆荷载被直接施加在地基表面.假设车轮荷载均匀分布在接触面上,轮胎与路面的实际接触面积的大致形状可以近似认为由一个矩形和两个半圆形组成,椭圆形接触面积可以等效为一个矩形,等效面积大小为0.3 m×0.24 m.
经调试,计算模型尺寸选取为8m×12m×8m(宽×长×高),网格尺寸取0.5m.为了最大程度降低边界条件对动荷载传播的影响,模型底部采用静态边界条件,4个侧面的边界采用自由场(即无限场地边界条件).自由场边界的实现方法是在模型四周生成一维和二维的网格,如图1a)所示,阻尼器将自由场网格和主体网格的侧边界耦合,自由场网格的不平衡力会施加到主体网格边界上.为了比对不同土层分布情况的区别,共建立了2种数值模型,一种为上硬下软型双层地基(如图1b)所示),一种为均质软土地基,均质软土地基计算参数与双层地基中下卧软土层相同(如图1c)所示).
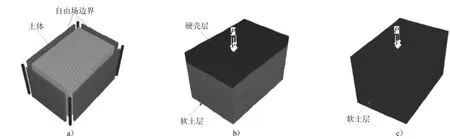
图1 数值计算模型Fig.1Numerical calculation model
土体本构模型采用Mohr-Coulomb模型(FLAC3D动力分析中允许采用静力本构模型,关键是设置好阻尼形式、边界条件等[11]),其土体计算参数如表1所示.
3 计算结果分析
3.1 动应力在不同土层中的传递规律
由图1b)所示计算模型,可以获取到交通荷载在硬壳层和下卧软土层中某一埋深位置处产生的应力时程曲线,如图2、图3所示;由图1c)所示计算模型,可以获取到交通荷载在均质软土中某一埋深位置处产生的应力时程曲线,如图4、图5所示.在图1b)和图1c)中坐标原点(x=y=0)定在荷载作用区域的中心,图2~图5所示应力时程曲线对应测点的坐标为(x=y=0,z),且纵坐标应力中包含了自重应力(埋深一定时,自重应力是一个定值),在计算动应力时应予以扣除.

表1 土体物理力学参数Tab.1Physical and mechanical parameters of soils
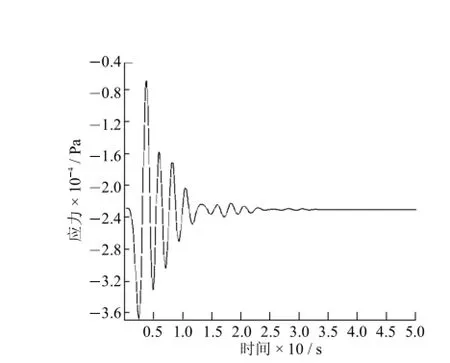
图2 硬壳层中应力时程曲线(z=1.25 m)Fig.2Stress-time curve in dry crust(z=1.25 m)

图3 下卧软土层中应力时程曲线(z=1.75 m)Fig.3Stress-time curve in subjacent soft soil layer(z=1.75 m)

图4 均质软土中应力时程曲线(z=1.25 m)Fig.4Stress-time curve in homogeneous soft soil(z=1.25 m)

图5 均质软土中应力时程曲线(z=1.75 m)Fig.5Stress-time curve in homogeneoussoft soil(z=1.75 m)
由图2~图5可知,受到车辆荷载作用后地基土不会立即产生震动,应力时程曲线波动出现短暂的滞后现象(此处可将滞后时间定义为某埋深处动应力的起振时间),在1.25 m埋深处起振时间约为0.01 s,在1.75 m埋深处起振时间约为0.025s.产生这种现象的主要原因是动应力沿垂直向传递需要一个时间过程,随着埋深的增加,这种动应力滞后现象愈加明显.由此可以估算出动应力的沿垂直向传递的平均速率.
4条应力时程曲线的波动规律近似,即受荷后时程曲线波动幅度明显增加(动应力出现峰值),停止加载后动应力有一个衰减过程,开始在自重应力值附近上下波动,最终衰减为0.当车辆荷载经过时,地基表面受到类似冲击荷载的作用,作用时间非常短,所产生的动应力持续时间也比较短暂.在上硬下软型双层地基模型中,动应力在硬壳层内(z=1.25 m)由最大值16 kPa衰减至0 kPa历时0.23 s,动应力平均衰减速率为69.6 kPa/s;动应力在下卧软土层中(z=1.75 m)由最大值3.5 kPa衰减至0 kPa历时0.2 s,动应力平均衰减速率为17.5 kPa/s.在均质软土模型中,动应力在z=1.25 m和z=1.75 m处的平均衰减速率为13kPa/s和5.2 kPa/s.可见,硬壳层的存在提高了动应力由峰值消散为0的速率.另外,应力水平的高低对于动应力衰减速率影响较大,动应力衰减速率呈现非线性变化特征,埋深浅处应力水平高,动应力衰减速率快;埋深大处应力水平低,动应力衰减速率慢.
动应力沿埋深方向的衰减规律较静应力情况有较大差别,在图2和图3中,当t=0.04s时刻附近,动应力从埋深1.25m传至1.75 m处,其数值由16 kPa衰减至3.5 kPa,动应力沿深度方向衰减率很快,大小为25 kPa/m;在图4和图5中,当t=0.05 s时刻附近,动应力从埋深1.25m传至1.75m处,其数值由5.2 kPa衰减至2.6 kPa,动应力衰减率降低为5.2 kPa/m.在静力荷载作用下,采用Boussinesq解求取该埋深范围的附加应力传递情况,其数值大小几乎没有变化.可见,动应力沿深度方向的衰减率较静应力明显迅速,硬壳层的存在提高了动应力沿深度方向的衰减率.
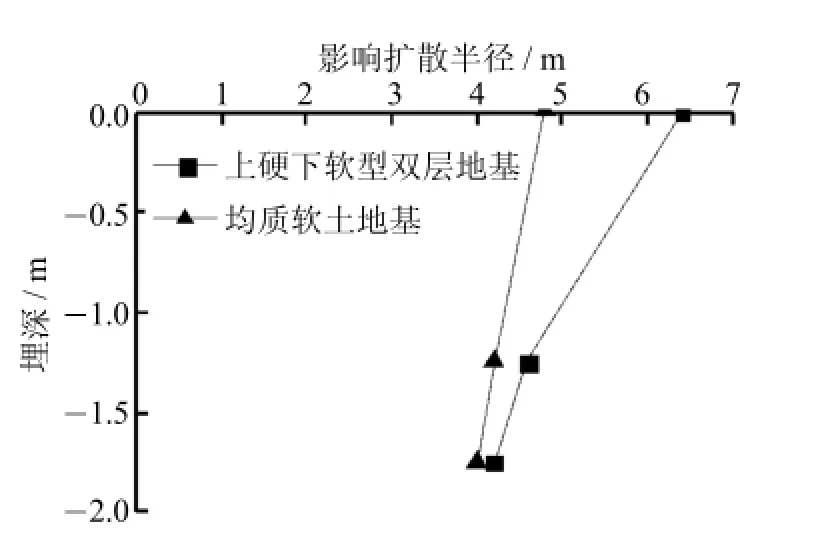
图6 影响扩散半径与埋深关系曲线Fig.6Relation curve between influence radius and buried depth
综合以上分析,表明上覆硬壳层能有效扩散和弱化动应力,这对于保障地基稳定性是有利的.
3.2 动应力影响扩散半径
采用程序运行中的模型监控命令hist,在某一埋深处,以荷载作用区域中心(x=y=0)为起点,在水平距离上以0.4m为间隔,记录各点的应力时程曲线,寻找各时程曲线中最大动应力小于0.1 kPa的点,认为此处不受动应力的影响,再反求出此单元到荷载作用区域中心的水平距离,即为动应力在该埋深处的影响半径.关键埋深处的动应力影响扩散半径如图6所示.
在图6中,动应力在上硬下软型双层地基中的影响扩散半径较均质软土地基要大,上覆硬壳层的存在增大了动应力的影响扩散范围,在地表处硬壳层中的影响扩散半径为6.4 m,而在均质软土中的影响扩散半径仅为4.8m,而随着埋深的增加,两者的差距在逐渐降低.
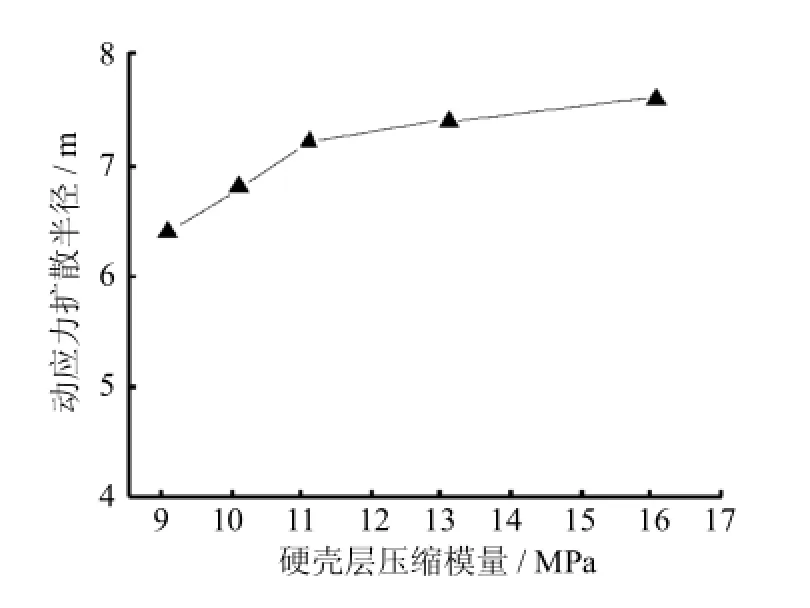
图7 压缩模量与动应力扩散半径关系曲线Fig.7Relation curve between influence radius and compression modulus
3.3 硬壳层特性对动应力扩散路径的影响
硬壳层的压缩模量是体现硬壳层特性的关键因素,通过绘制硬壳层压缩模量与动应力扩散半径、土层交界面动应力之间的关系曲线,可以近似揭示硬壳层特性对动应力扩散性的影响规律,如图7、图8所示.
由图7可知,随着硬壳层压缩模量的增大,动应力在地表处的水平向扩散半径呈现扩大的趋势.这说明,上覆硬壳层性质越好,对动应力水平方向的扩散性越有利,但随着硬壳层压缩模量的增大,动应力的扩散半径增长速度在逐渐变慢.由图8可知,随着硬壳层压缩模量的增大,传递至硬、软土层交界面处的动应力在减小.这说明,上覆硬壳层性质越好,对动应力垂直向的扩散性同样有利,而这种动应力减小的趋势随着硬壳层压缩模量的增大也在减弱.综合以上分析,上覆硬壳层的存在对于改善动应力在地基土中的扩散路径起到了积极作用,可以说,这是硬壳层壳体效应在动力范畴内的一种具体表现.

图8 压缩模量与土层交界面动应力关系曲线Fig.8Relation curve between influence radius and dynamic stress in soil layer interface
3.4行车速度对动应力传递的影响
行车速度可能是影响动应力传递的因素之一,为了研究两者之间的量化关系,绘制了行车速度与动应力传递关系曲线,如图9所示.
由图9可知,随着行车速度的增大,传递至硬、软土层交界面处的动应力随之增长,但是行车速度对于动应力的传递影响很小,行车速度每增加30km/h,动应力仅增加0.01kPa.因此,在分析交通荷载作用下的地基土动力响应时,行车速度仅作为一个次要因素考虑.
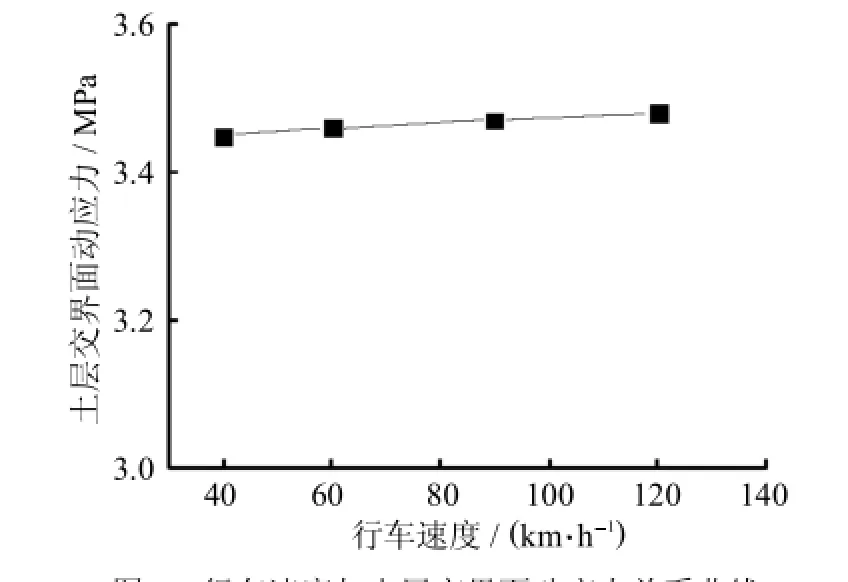
图9 行车速度与土层交界面动应力关系曲线Fig.9Relation curve between vehicle speed and dynamic stress in soil layer interface
4 结论
1)数值模拟方法是研究地基土动力学特性的主要手
段之一,以FLAC3D为例,在模型构建和求解过程中,应对荷载表达式、模型尺寸、阻尼形式、计算参数及边界条件等诸多方面进行科学设置,这是保障计算结果合理性的重要前提条件.
2)交通荷载作用下产生的动应力在地基土中的传递规律表现出以下特征:不同埋深处,应力时程曲线波动出现短暂的滞后现象;应力水平的高低以及有无硬壳层对于动应力衰减速率影响较大,动应力衰减速率呈现非线性变化特征;动应力沿深度方向的衰减速度较静应力明显迅速.
3)在静力范畴,上覆硬壳层对下卧软土层起到了应力扩散作用,具有很大的力学潜能可以挖掘.同样,在动力范畴,上覆硬壳层的存在增大了动应力的影响扩散半径,且对改善动应力在地基土中的扩散路径起到了积极作用.上覆硬壳层能有效扩散和弱化动应力,这对于保障地基稳定性是有利的.
4)在分析交通荷载作用下的地基土动力响应时,行车速度仅作为一个次要因素考虑,其数值大小对计算结果的影响不大.
[1]刘雪珠,陈国兴.轨道交通振动下南京片状细砂的有效应力路径及破坏模式[J].岩土力学,2010,31(3):719-726.
[2]AUERSCH L.The effect of critically moving loads on the vibrations of soft soils and isolated railway tracks[J].Journal of Sound and Vibration,2008,3l(3):587-607.
[3]彭月明,张铁壮,窦远明.硬壳层对软土地基沉降特性影响的研究[J].河北工业大学学报,2007,36(1):101-105.
[4]曹海莹,窦远明.上硬下软型双层路基应力扩散特征及工程应用[J].公路交通科技,2012,29(2):29-34.
[5]李义,袁富强.列车动荷载作用下土的动力特性分析[J].天津城市建设学院学报,2010,16(1):25-28.
[6]陈剑,苏跃宏.交通荷载作用下公路路基动力特性的数值模拟研究[J].公路交通科技,2011(5):44-48.
[7]徐明江,魏德敏.非饱和土地基的三维非轴对称动力响应[J].工程力学,2011,28(3):78-85.
[8]卢正,王长柏,付建军,等.交通荷载作用下公路路基工作区深度研究[J].岩土力学,2013(2):316-321.
[9]卢正,姚海林,吴万平,等.高速公路路基结构分析及动变形设计方法[J].岩土力学,2010(9):2907-2912.
[10]张艳美,梁波.几何不平顺条件下高速公路路基的动态响应[J].兰州铁道学院学报,2001(4):66-69.
[11]陈育民,徐鼎平.FLAC/FLAC3D基础与工程实例[M].第2版.北京:中国水利水电出版社,2013:210-212.
[责任编辑 杨屹]
Dynamic response characteristics of soft subgrade covering dry crust under traffic load
CAO Haiying1,LIU Yunfei1,REN Xiaojun2,3,LI Yunong1
(1.School of CivilEngineeringandMechanics,YanshanUniversity,HebeiQinhuangdao066004,China;2.School of CivilEngineering, Hebei University of Technology,Tianjin 300401,China;3.TianjinRailway Technical and Vocation College,Tianjin 300240,China)
soft subgrade;dry crust;traffic load;numberical simulation;dynamic response
By means of dynamic analysis function in numberical simulation software FLAC3D,the procedure was written for building and solving computational model,then the dynamic response of soft subgrade covering dry crust under traffic load was analyzed.The law of dynamic stress transfer shows the following features in foundation soil under traffic load: the waveofstress-time curves appears transient hysteresis indifferent buried depth;the speedofdynamicstressattenuation is mainly affected by stress level and dry crust existence,and it shows nonlinear characteristics;the attenuation rate of dynamic stress is obviously faster than that of static stress with depth;Because of dry crust existence,the influence radius of dynamic stress is expanded,and the diffusion path of dynamic stress is improved.
1007-2373(2015)03-0094-05
10.14081/j.cnki.hgdxb.2015.03.018
2014-10-11
国家自然科学基金(51308486);河北省博士后择优资助科研项目(D2014003010);河北省高等学校科学研究青年基金(Q2012156)
曹海莹(1979-),男(汉族),副教授,博士,chyysu79@126.com.
TU435
A
