部分延迟订购的易变质品联合定价与生产策略
2015-07-07霍佳震李贵萍段永瑞
霍佳震, 李贵萍, 段永瑞
(同济大学 经济与管理学院,上海 200092)
部分延迟订购的易变质品联合定价与生产策略
霍佳震, 李贵萍, 段永瑞
(同济大学 经济与管理学院,上海 200092)
构建了一个需求同时依赖于销售价格和库存水平,生产率和变质率均为常数,允许缺货且缺货量部分延迟订购的易变质品联合定价与生产控制模型。首先证明了在销售价格给定的情况下,系统的总利润函数是关于生产计划的严格凹函数,平均利润函数是严格的伪凹函数,即存在唯一的最优解,并给出其充分条件。接着给出问题的一个数值求解算法。最后通过算例,展示了模型及相关算法的应用,并对相关参数进行了灵敏度分析,结果显示:当产品的生产成本、缺货成本和机会成本增加时,系统的平均利润将下降;生产成本和延迟订购阻力系数对最优定价和生产策略以及平均利润的影响较大。
供应链管理;联合定价与生产策略;非线性规划;易变质品;部分延迟订购
0 引言
在库存控制模型中,需求模型的构建是重中之重。构建的需求模型能否有效地反映现实情况,是考查所构建的库存模型准确与否和所提出的最优控制策略是否有效的重要指标。如Lau和Lau[1]所述,在很多情况下,需求上的微小变化可能会导致最优库存决策上很大的不同。因此,不同的需求模型所对应的最优策略也会有很大差异。事实上,影响需求的因素多种多样,有服务水平、广告投入、产品质量、品牌、价格、时间、营销策略等等。经典的确定性库存模型多假设产品的需求率为常数或与时间变化相关。然而,我们注意到,现实生活中有一类商品的需求受库存水平的影响,如日常生活中常见的果蔬、面包等,以及节日的礼品(如端午的粽子、中秋的月饼等)和快销时尚品(如ZARA、优衣库等时装品牌)等生命周期较短的易变质品,较高的库存水平能够带来较大的需求。针对这一现象,Levin等[2]提出“需求受库存水平影响”的观点。此后,很多学者研究了此类物品的库存优化问题。Chung等[3]研究了当商品的需求受库存水平线性影响、变质率为常数,缺货量完全延迟订购和完全损失两种情况下的库存系统,分别给出系统存在唯一最优解的充分必要条件。Teng等[4]构建了需求率与库存水平相关,变质率为常数,不允许缺货且期末库存水平不为零的EOQ模型。Hou[5]在需求与库存水平线性相关,变质率为常数,允许缺货且短缺量完全延迟订购的假设基础上,建立了一个有限时域内考虑通货膨胀与资金时间成本的易变质品库存模型。Duan等[6]假设需求依赖于库存水平,变质率为常数,按照持有库存是否有利,在不同的条件下分别构建了不允许缺货和允许缺货且缺货量部分延迟订购情况下的易变质品库存模型。Urban[7]给出了一个需求依赖于库存水平的相关文献综述。
众所周知,产品的需求在很大程度上受到销售价格的影响,通常价格越高,需求会越小;反之,则越大。在日常生活中,我们常常观察发现,物品的大量摆放往往跟产品的促销和降价相关联。比如,面对各大超市或卖场的促销活动,以及农贸市场上整车的蔬菜和水果的贩卖,消费者的第一反应就是便宜,因此会招来大量顾客前来询问或购买。因此,同时考虑物品的库存水平和销售价格对需求的影响具有一定的现实意义。Urban和Baker[8]假设产品需求与价格、时间和库存水平同时相关,在不考虑系统缺货的情况下,构建了相关库存模型。Datta和Paul[9]分析了一个有限时域内需求同时受库存水平和销售价格影响且不允许缺货的库存系统。Hou和Lin[10]考虑通货膨胀和货币的时间价值,假设产品的变质服从指数分布,需求同时受库存水平和价格的影响,缺货量完全延迟订购,构建了一个有限时域内的库存模型。You和Hsieh[11]考虑企业在有限的计划时域内销售季节性产品的情况,假设需求与库存水平和产品价格同时相关,并且在有限的时域内允许多次价格变化,构建了一个不允许缺货的联合定价和库存控制模型。沿袭经典EOQ模型的假设,以上模型均采用缺货时短缺量要么完全损失要么完全延迟订购的假设。如此假设的优点是可以简化模型,着重分析关键因素对最优策略的影响;缺点是忽略了一些现实现象,没有很好地反应真实的库存系统。现实中,当缺货发生时通常有一些顾客愿意等待直到下一次补货到达,而另外一些顾客因为不愿意等待而去寻找别的商家购买,即“部分延迟订购”。然而,当考虑部分延迟订购的情况时,库存系统的成本构成中将增加由延迟订购的需求部分引起的缺货成本和因损失销售部分带来的机会成本,从而增加模型构建的复杂性以及在最优解的存在性及唯一性等数学证明上的困难性。
在产品价格保持不变的情况下,考虑到顾客大多不愿意等待的这种心理状态,Abad[12]提出缺货时的部分延迟订购率与顾客等待时间负相关的观点,同时给出了两种不同形式的部分延迟订购率:一种是等待时间的负指数函数K0e-K1τ;另一种是等待时间线性函数的倒数K0/(1+τK1),其中τ为等待时间,且满足τ>0,0
此外,可以发现上述相关研究均集中在关于产品订购的库存控制问题上,很少涉及到生产问题。Abad[17]构建了一个生产率与变质率均为常数的易变质品定价和生产联合决策模型,其中考虑了缺货量部分延迟订购的情况,但在其成本构成中并未考虑缺货成本和机会成本,同时需求仅与价格相关。Teng和Chang[18]也针对易变质品提出了一个生产率和变质率均为常数的联合定价和生产模型,虽然假设产品的需求与库存水平和价格同时相关,但系统不允许缺货。综上,鉴于理论研究的空缺和现实情况的需要,本文同时将需求受价格和库存水平影响以及缺货量部分延迟订购的情况考虑在内,构建了一个易变质品的联合定价与生产模型。模型假设产品以固定的生产率进行生产,变质服从指数分布,即变质率为常数,需求与库存水平和销售价格同时相关,系统允许缺货且部分延迟订购率是顾客等待时间的负指数函数。进一步,证明了模型解的存在性,并提出相应的数值求解算法,最后通过算例,展示了模型和算法的应用,并对主要参数进行了相关的灵敏度分析。
1 模型
这一部分包括三个小节,1.1小节主要介绍构建模型时用到的相关假设和符号表示;1.2小节是关于联合定价与生产模型的构建;1.3小节是关于所构建模型的最优解分析。
1.1 假设与符号表示
(1)计划时域无限且系统的订货提前期为零。
(2)I(t) 表示在t∈[0,T+λ]时刻的库存水平。T(T≥0)表示在生产周期内库存水平为非负的时间段长度;λ(λ≥0)表示库存水平为负,即缺货情况下的时间段长度;γ和ψ表示一个生产周期内中间过渡的时间段,如图1所示。其中,T和λ为决策变量。
(3)需求率是关于销售价格p和即时库存水平I(t)的函数,表示为:

其中,α(p)是关于销售价格p的任意非负减函数;β(0<β<1)是一个非负常数,表示受库存水平影响的产品需求率参数。
(4)产品的变质率为常数,表示为θ(0<θ<1)。
(5)产品的生产率K有限且为常数,满足K>D(p,I(t))+θI(t)。
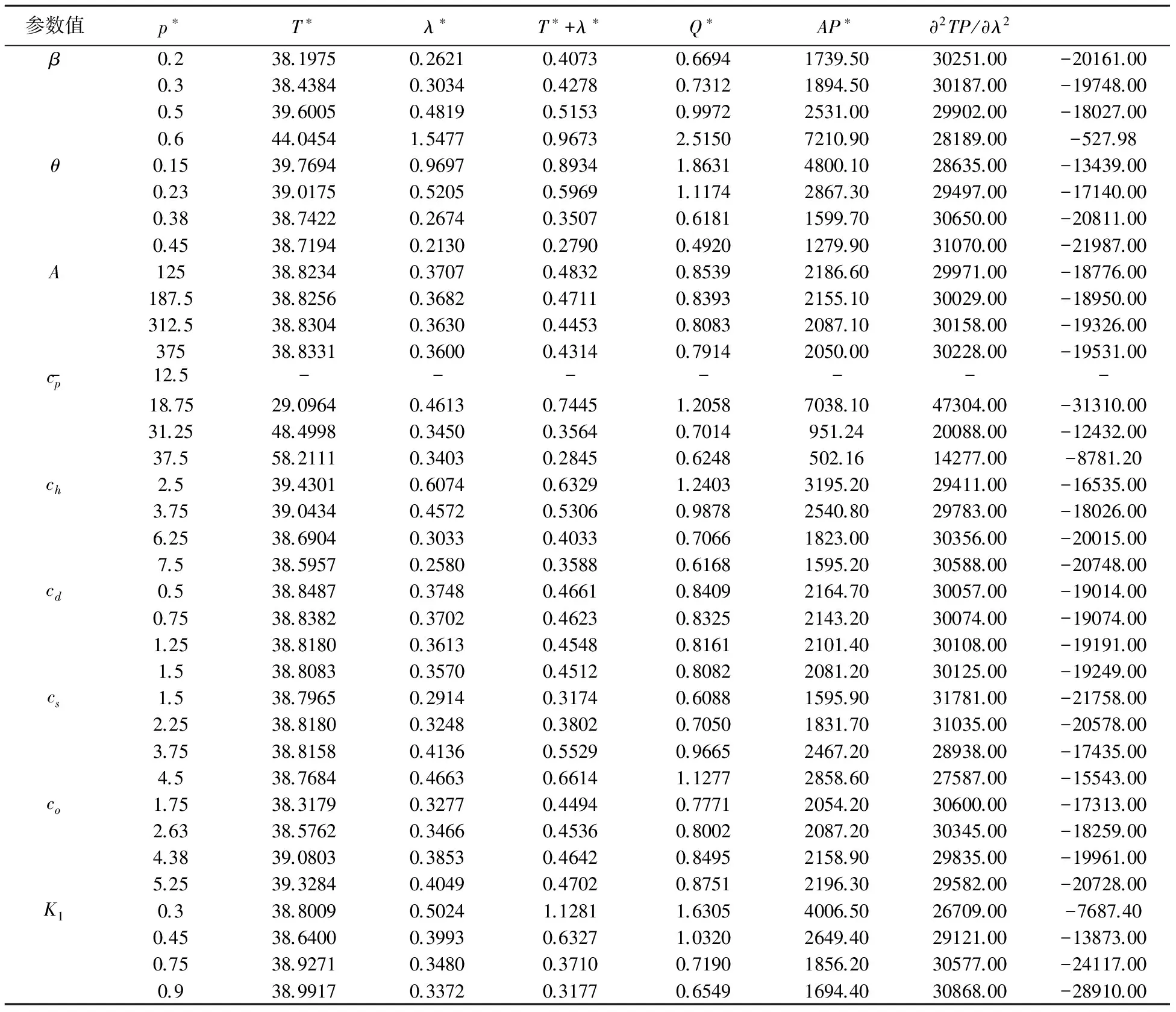
(6)系统允许缺货且缺货量部分延迟订购。部分延迟订购率与等待时间相关,满足B(τ)=K0e-K1τ,0 (7)Q表示一个周期内系统的总生产量;A表示每个生产周期的生产准备成本;cp表示单位产品的生产成本,ch表示单位产品单位时间的库存持有成本,cd表示单位变质产品的处理成本,cs表示单位产品单位时间的缺货成本;co表示损失单位销售导致的机会成本;TP表示一个生产周期内库存系统的总利润;AP表示单位时间的平均利润。 1.2 模型构建 图1所示为一个生产周期内系统的库存水平随时间的变化趋势。假设生产从t=0时刻开始,此时系统的库存水平为I(0)=0。随着生产的进行,库存在满足当时的需求和变质后开始累积,在t=γ时刻库存水平达到最高,停止生产。接着,由于需求和变质的共同作用,库存水平逐渐下降,在t=T时刻库存水平下降到0,即I(T)=0。此后,系统处于缺货状态,库存水平为负并继续下降,经过时间段ψ,在t=T+ψ时刻,库存缺货水平达到最大。这时生产重新开始,到t=T+λ时刻,累积的缺货量以及现有的需求全部被满足,库存水平再次达到0,即I(T+λ)=0。 通过以上描述,库存水平I(t)关于时间的变化可以用下列微分方程来描述,其中α和α(p)等价。 当t∈[0,γ],库存水平I(t)满足: (1) 已知边界条件I(0)=0,求解微分方程(1)得: (2) 图1 补货周期内库存水平随时间变化的趋势图 当t∈[γ,T],库存水平I(t)满足: (3) 已知边界条件I(T)=0,求解微分方程(3)得: (4) 由(2)和(4)有: 求解得: (5) 从T时刻开始系统发生缺货,假设对于未满足的需求,采用“先到先得”的原则,即先到的需求在有货时将先被满足。如图1所示,在时间段[T,T+ψ]内没有进行生产,只有延迟订购的需求,所以当t∈[T,T+ψ]时,等待时间为τ=(T+ψ)-t-I(t)/K。在t=T+ψ时刻生产重新开始,所以当t∈[T+ψ,T+λ]时,顾客的等待时间为τ=-I(t)/K。 因此,当t∈[T,T+ψ],库存水平I(t)满足: (6) 已知边界条件I(T)=0,求解微分方程(6)得: (7) 由(7)可得: (8) 当t∈[T+ψ,T+λ],库存水平I(t)满足: (9) 以(8)式为边界条件,得 (10) 将I(T+λ)=0代入(10),有: (11) 求解(11)得到: (12) 此外,由于系统只在时间段[0,γ]和[T+ψ,T+λ]内以常数生产率K进行生产,因此,一个生产周期内系统的总生产量为: Q=K[γ+(λ-ψ)] (13) 综上可知,系统利润的各构成要素分别为: (1)生产准备成本=A 因此,系统一个周期内的总利润为: (14) 那么,系统的平均利润为: (15) 1.3 最优解分析 系统的目的是确定最优的T、λ和p,使系统的平均利润AP(T,λ,p)达到最大。可知,系统的平均利润((15)式)存在最优解的必要条件是: (16) (17) (18) 首先讨论销售价格p预先给定的情况,该情况适用于生产者不能随意制定产品价格的情形,比如生产者处于竞争激烈的市场中时,产品的销售价格是由市场决定的。此时分别用TP(T,λ|p)和AP(T,λ|p)表示(14)和(15)式给出的系统总利润和平均利润。有如下结论: 定理1 对于任意给定的销售价格p,如果β(p-cp)-θ(cp+cd)-ch<0,那么TP(T,λ|p)((14)式)是关于T和λ的严格凹函数。 证明见附录。 定理1中的条件β(p-cp)-θ(cp+cd)-ch<0等价于β(p-cp)<θ(cp+cd)+ch,从管理角度来看,其中β(p-cp)可理解为从持有单位库存获取的收益,而θ(cp+cd)+ch可看作是持有单位库存需要付出的成本。因此,如果β(p-cp)-θ(cp+cd)-ch<0,说明持有单位库存带来的收益要小于需要付出的成本,那么此时允许缺货策略对系统将是有益的。因此,该条件是模型成立的前提。 定理2 如果TP(T,λ|p)((14)式)是关于T和λ的严格凹函数,那么AP(T,λ|p)((15)式)是关于T和λ的严格伪凹函数。 由定理1和定理2可知,对于任意给定的p,当满足β(p-cp)-θ(cp+cd)-ch<0时,平均利润AP(T,λ|p)((15)式)存在唯一的全局最大值,最大值点可以通过求解由(16)和(17)构成的方程组得到。 接下来讨论给定T和λ,销售价格p为决策变量的情况。此时用AP(T,λ|p)表示(15)式所示的平均利润。由于函数的复杂性,很难从解析角度证明AP(p|T,λ)是关于p的凹函数,但由p>cp和β(p-cp)-θ(cp+cd)-ch<0可得,cp 虽然招标投标活动程序完备,但因投标单位数量过多造成一定的混乱,严重影响投标秩序。对于一个投资不大、规模较小的建设项目来说,多家单位竞争致使中标率低,有的甚至只有2%,这就造成了很多单位和个人在估计自己不中标的情况下,抱着恶意竞标、浑水摸鱼、搅乱市场的心态参加投标,给招标投标市场制造了一定的混乱。 为了求解系统最优的联合定价和生产策略,即确定最优的T、λ和p,使系统的平均利润AP(T,λ,p)((15)式)最大化,根据以上分析与结论我们在下一节给出了一个求解模型最优解的数值算法。 第1步 令p=pi并从i=1开始,即令p=pi作为初始值,且cp 第2步 对于任意给定的p=pi,运用MATLAB中的FSOLVE函数或牛顿法,求解由(16)和(17)构成的方程组,将结果标记为(Ti,λi); 第3步 令(T,λ)=(Ti,λi),用二分法求解(18)式,将求解结果标记为pi+1; 第4步 分别计算AP(Ti,λi,pi)和AP(Ti,λi,pi+1),标记为AP1和APi+1并进行比较。如果满足AP(Ti,λi,pi)≥AP(Ti,λi,pi+1),那么最优解为(T*,λ*,p*)=(Ti,λi,pi);否则,令i=i+1,返回第2步。 第5步 将最优解(T*,λ*,p*)代入(13)式,可得到一个生产周期内系统的最优生产量。 这一部分主要展示所提出的模型和算法的具体数值应用,以及一些主要参数的灵敏度分析,算法通过MATLAB来实现。 考虑一个生产系统,相关参数取值分别为:α(p)=1.6×108p-3件,β=0.4,θ=0.3,K=50000件,A=250元,cp=25元/件,ch=5元/件/天,cd=1元/件,cs=3元/件/天,co=3.5元/件,K0=0.9,K1=0.6。 表1 算例的迭代过程和计算结果 接下来研究相关参数的灵敏度,保持其它参数的取值不变,每次仅改变指定参数的取值。计算结果如表2所示。 表2 相关参数的灵敏度分析 观察表2,容易得到以下结论: (1)随着β的增大,最优销售价格p*、最优库存持有时间T*、最优缺货时间λ*以及系统的最优生产周期T*+λ*、最优生产量Q*均逐渐增大,而平均利润AP*逐渐减小。这是因为当β增大时,单位库存带来的需求也将增加,所以需要生产更多的产品以提高库存水平,即最优生产量Q*将增大,因而最优库存持有时间T*也将增加,整个生产周期也随之增大,从而导致平均利润下降。结果表明当产品的需求受库存水平影响较大时,管理者采用增加生产量、提高销售价格的管理策略是有利的。 (2)随着变质率θ、库存持有成本ch和变质处理成本cd的增大,最优销售价格p*、最优库存持有时间T*、最优缺货时间λ*以及系统的最优生产周期T*+λ*、最优生产量Q*均逐渐减小,而平均利润AP*逐渐增大。当产品的变质率、变质处理成本或库存持有成本较大时,越多的库存将引起越大的变质成本或库存持有成本,因此需要减少产品的生产量,并通过降低销售价格来增加需求量,使产品尽可能快的销售出去,从而持有库存的时间将缩短,平均利润将增大。也就是说,当持有产品的成本(包括变质成本和持有成本)较大时,管理者应采用减少库存量同时降低销售价格的策略。 (3)随着生产准备成本A的增大,最优销售价格p*和平均利润AP*逐渐增大,但最优库存持有时间T*、最优缺货时间λ*以及系统的最优生产周期T*+λ*和最优生产量Q*均逐渐减小。当生产准备成本较大时,产品的销售价格相应也会增加,因此,需求将下降,从而需要减少生产量,缩短库存持有时间。但可以看出最优定价和生产策略以及平均利润对生产准备成本的变化的敏感度较差。 (4)随着生产成本cp的增大,最优销售价格p*逐渐增大,但最优库存持有时间T*、最优缺货时间λ*以及系统的最优生产周期T*+λ*、最优生产量Q*和平均利润AP*均逐渐减小。与实践经验相一致,产品的生产成本越高,其最优销售价格也越高,从而导致需求下降,最优生产量减少,最优生产周期缩短、系统的平均利润下降。需要特别注意的是,最优定价和生产策略以及最优平均利润对生产成本的变化非常敏感。 (5)随着缺货成本cs和机会成本co的增大,最优库存持有时间T*、最优缺货时间λ*、最优生产周期T*+λ*、最优生产量Q*均逐渐增大,但平均利润AP*逐渐减小。当缺货成本和机会成本较大时,系统需要通过生产较多的产品来将由缺货带来的损失降到最低。此外,最优定价和生产策略以及平均利润对缺货成本和机会成本的变化较敏感。 (6)随着延迟订购阻力系数K1的增大,最优库存持有时间T*、最优缺货时间λ*、最优生产周期T*++λ*、最优生产量Q*均逐渐减小,但平均利润AP*逐渐增大。此外,延迟订购阻力系数的变化对最优生产策略和平均利润的影响较大,而对最优定价的影响很小。因此,对于延迟订购系数不同的产品或销售群体,其对应的定价和生产策略也将有很大差异,需要引起生产管理者的注意。 对于生命周期较短的易变质品来说,如果蔬、面包、节日礼品和快销时尚品等,其需求不仅受价格的影响而且与库存水平相关。另外,对于此类商品,缺货发生时有些顾客愿意接受延迟交付,而有些不愿意,即适用于“部分延迟订购”的情况。然而,已有文献中却没有考虑过有关这一现象的生产系统。鉴于此,针对以上描述的系统,本文考虑了一个易变质品的联合定价与生产决策问题,在理论上填补了这一空白。具体假设产品以固定的生产率进行生产,以固定的变质率发生变质,需求同时受产品销售价格和库存水平的影响,系统允许缺货,当缺货发生时短缺量部分延迟订购。进一步在系统的成本结构中增加了缺货成本和因损失销售而引起的机会成本,构建相应模型使其成本构成更加完善,也由此进一步增加了模型构建的复杂性和数学证明上的困难性。针对这一难点,本文运用数学和算例相结合的方法给出了相关证明,得出当产品的销售价格给定时,当参数满足一定条件时,系统存在最优的生产策略使系统的平均利润达到最大。接着给出了一个求解系统最优生产和定价联合策略的数值算法,可为生产者提供决策上的支持和帮助。最后通过算例,展示了模型和算法的应用并对相关参数的灵敏度进行了分析,得到一些有用的关于定价与生产管理的结论,为生产者提供了一些相关的管理建议。此外,本文的研究还存在一定的不足,比如假设产品的生产率和变质率均为常数,而现实中,产品的生产率可能会根据产品的季节需求或库存水平进行调整,而产品的变质率也会随时间发生变化。这些都是需要在未来研究中改进的地方。另外,允许产品的价格在销售周期内动态变化的情况也是未来的研究方向之一。 [1] Lau A H, Lau H S. Effects of a demand-curve’s shape on the optimal solutions of a multi-echelon inventory/pricing model[J]. European Journal of Operational Research, 2003, 147: 530-548. [2] Levin R I, Mclaughlin C P, Lamone R P, Kottas J F. Productions/operations management: contemporary policy for managing operating systems[M]. New York: Mc Graw-Hill, 1972. [3] Chung K J, Chu P, Lan S P. A note on EOQ models for deteriorating items under stock dependent selling rate[J]. European Journal of Operational Research, 2000, 124: 550-559. [4] Teng J T, Ouyang L Y, Cheng M C. An EOQ model for deteriorating items with power-form stock-dependent demand[J]. Information and Management Sciences, 2005, 16 (1): 1-16. [5] Hou K L. An inventory model for deteriorating items with stock-dependent consumption rate and shortages under inflation and time discounting[J]. European Journal of Operational Research, 2006, 168: 463- 474. [6] Duan Y, Li G, Tiem J M, Huo J. Inventory models for perishable items with inventory level dependent demand rate[J]. Applied Mathematical Modelling, 2012, 36: 5015-5028. [7] Urban T L. Inventory models with inventory-level-dependent demand: a comprehensive review and unifying theory[J]. European Journal of Operational Research, 2005, 162: 729- 804. [8] Urban T L, Baker R C. Optimal ordering and pricing policies in a single-period environment with multivariate demand and markdowns[J]. European Journal of Operational Research, 1997, 103: 573- 83. [9] Datta T K, Paul K. An inventory system with stock-dependent, price-sensitive demand rate[J]. Production Planning & Control: The Management of Operations, 2001, 12: 13-20. [10] Hou K L, Lin L C. An EOQ model for deteriorating items with price- and stock-dependent selling rates under inflation and time value of money[J]. International Journal of Systems Science, 2006, 37: 1131-1139. [11] You P S, Hsieh Y C. An EOQ model with stock and price sensitive demand[J]. Mathematical and Computer Modelling, 2007, 45: 933-942. [12] Abad P L. Optimal pricing and lot-sizing under conditions of perishability and partial backlogging[J]. ManagementScience, 1996, 42(8): 1039-1104. [13] Abad P L. Optimal price and order size for a reseller under partial backordering[J]. Computers & Operations Research, 2001, 28: 53- 65. [14] Dye C-Y. Joint pricing and ordering policy for a deteriorating inventory with partial backlogging[J]. Omega, 2007, 35: 184-189. [15] Papachristos S, Skouri K. An inventory model with deteriorating items, quantity discount, pricing and time-dependent partial backlogging[J]. International Journal of Production Economics, 2003, 83: 247-256. [16] Hsieh T P, Dye C Y. Pricing and lot-sizing policies for deteriorating items with partial backlogging under inflation[J]. Expert Systems with Applications, 2010, 37: 7234-7242. [17] Abad P L. Optimal pricing and lot-sizing under conditions of perishability, finite production and partial backordering and lost sale[J]. European Journal of Operational Research, 2003, 144: 677- 685. [18] Teng J T, Chang C T. Economic production quantity models for deteriorating items with price- and stock-dependent demand[J]. Computers &Operations Research, 2005, 32: 297-308. Joint Pricing and Production Policy for Deterioration Items with Partial Backlogging HUO Jia-zhen, LI Gui-ping, DUAN Yong-rui (SchoolofEconomicsandManagement,TongjiUniversity,Shanghai200092,China) In this paper, we develop a joint pricing and production model for deterioration items in which we assume that the demand rate is dependent both on the selling price and the inventory level, the production rate and the deterioration rate are known and constant and the unmet demand is partial backlogged in the shortage period. We first prove that for any given selling price, the total profit function is strictly concave, and the average profit function is strictly pseudo-concave, that is, there exists the unique and optimal solution to the problem, and the sufficient condition is also presented. Then an algorithm is proposed to obtain the optimal solution of the problem. At last, we give a numerical example to illustrate the application of the model and algorithm proposed, and then we also conduct the sensitivity analysis on the parameters. The results show that when the production cost, the shortage cost and the opportunity cost of items increase, the average profit of system will decrease. The optimal pricing-production policy and the average profit are highly sensitive to the production cost and the backordering resistance. supply chain management; joint pricing and production policy; nonlinear programming; deterioration items; partial backlogging 2012-12-19 国家自然科学基金项目(71002020,71371139,71371140);上海浦江人才计划(12PJC069);中央高校基本科研业务费专项资金 霍佳震(1962-),男,上海,博士,教授,研究方向:供应链管理与服务运作管理等。 F253.4 A 1007-3221(2015)01- 0255- 08
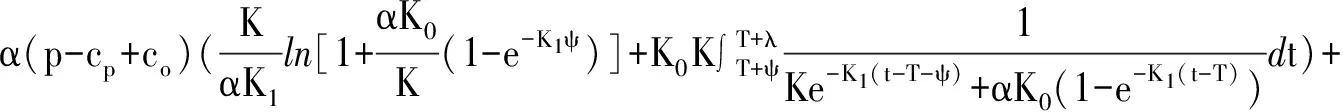
2 算法
3 算例分析

4 结论
