考虑协同效应的突发事件救援人员分组方法

叶 鑫, 王 雪， 仲秋雁

(大连理工大学 管理科学与工程学院，辽宁 大连 116024)



考虑协同效应的突发事件救援人员分组方法

叶 鑫, 王 雪， 仲秋雁

(大连理工大学 管理科学与工程学院，辽宁 大连 116024)

针对突发事件的应急救援人员分组问题，提出了一种考虑人员间协同效应的应急救援人员分组方法。首先，对突发事件应急救援人员分组问题进行了描述。然后，基于系统协同理论的思想，提出了救援小组的协同度模型，定量化的度量救援人员间的协同效应。进一步地，综合考虑救援人员的基础效能与协同效应，基于协同度模型给出了救援人员完成不同任务的实际效能的表达式。在此基础上，以最大化各救援小组的实际效能为目标，构建了突发事件应急救援人员分组的优化模型，并给出了将这一多目标0-1二次规划模型转换为单目标0-1线性规划模型的方法，进而可求解并确定救援人员的最优分组方案。最后，通过一个实例分析说明了本文所提出方法的可行性和有效性。

应急管理；救援人员分组；协同效应；优化模型

0 引言

近年来，突发事件频发，造成了大量的人员伤亡和财产损失，对社会造成了严重危害。如2008年南方雪灾、汶川地震、2010年大连油管爆炸、2013年雅安地震等。突发事件爆发后，相关部门会立即派出救援人员，对灾区实施紧急救援。人员分组是应急救援开始阶段的重要决策问题之一。救援人员在实施具体救援任务的过程中，除发挥其基础技能所带来的基础效能外，救援人员间的相互协作亦会产生协同效应，简单的说，就是“1+1>2”的效应。因此，如何依据救援人员的基础效能和人员间的协同效应，科学、合理地将救援人员进行分组，以实现救援任务的完成“效果”最佳，是一个具有实际价值的研究问题。

目前，有关应急救援人员分组问题的相关研究已取得一定进展，如樊治平等人提出的根据救援人员综合表现值进行人员分组的方法[1]，以及考虑应急救援时间满意度与人员胜任程度等的突发事件应急救援人员的派遣模型[2]，但均没有考虑人员间的协同效应。而很多国内外相关学者认为协同在突发事件应急管理中已变得越来越重要。其中，刘奕等人通过实验和案例分析指出，相比无协同，组织、部门和人员间的协同将使应急救援的效果更好[3]。陈兴等人在考虑部门协同的基础上，利用部门之间和部门内部打分建立了部门的应急协同决策模型[4]。Naim Kapucu等人在研究中强调了协同应急管理的重要性[5]。Rui Chen等人给出了应急响应管理中的协同框架[6]。Liaquat Hossain等人提出了一个在复杂动态环境下协同建模的设计框架和思想[7]。但这些相关研究主要从定性角度分析，定量角度研究较少，且没有给出协同度模型，不便于定量化度量协同效应。在协同度研究方面，现有协同度模型包括基于隶属函数、离差系数最小化、基尼系数和距离的协同度模型等[8～10]。需要指出的是，已有的协同度计算方法大都应用于经济系统分析和发展研究，具有计算相对复杂且所需数据量大等特点。而突发事件具有偶然性，且需在较短时间内快速确定应对方案并实施救援活动，现有协同度模型不适合直接应用于突发事件应急管理中。

由于基于距离的协同度模型可体现协同本质、具有较强的普适性[8]且计算简便、所需数据量较少，同时考虑到协同具有“放大”作用[11]，因此，本文提出了一种基于欧氏距离平方的协同度模型。进而，考虑到不同的救援人员分组方案可能导致救援人员的实际效能不同，因此利用该协同度模型构建救援人员实际效能表达式和人员分组模型，并对模型进行变换求解。

图1 突发事件应急救援人员协同分组问题示意图

1 问题描述

在应急救援中，救援队伍往往要完成若干项救援任务。因此需要根据不同任务的需求，将救援队伍划分成若干个救援小组，每个救援小组通过成员间的协同完成一项救援任务。在救援过程中，救援人员所具备的基础技能达到某项任务要求的程度为其基础效能，救援人员间的协同效应对于救援人员基础效能的发挥和救援任务的实际完成效果具有重要作用。即救援人员针对不同救援任务的基础效能可能不同，并且当某一救援人员被指派到某一具体的救援小组时，由于组内其他人员构成可能不尽相同，导致组内协同效应可能不同，从而导致该救援人员的实际效能可能不同。因此，本文所要解决的问题是：针对救援任务需求，根据救援人员的协同特征和技能特征，考虑救援人员的协同效应和基础效能，在救援人员实际效能分组前不确定的情况下，如何将救援人员合理地分配到各救援小组中完成相应任务，以充分发挥救援人员间的协同效应，最大限度地利用救援人员的实际效能，从而保证人员的合理分配，使全部救援任务的完成“效果”最佳，并要求每个救援人员最多只能被分配到一个救援小组中，且每个救援小组被分配的人员数量满足救援任务的人数需求，如图1所示。

下列符号用来表示突发事件应急救援人员分组的相关集和量：

P={Pi|i=1,2,…,n}：救援队伍中可供选择的救援人员集合，其中Pi表示第i个救援人员，如地震应急救援中的医生、护士、搜救人员等。

T={Tg|g=1,2,…,m}：救援过程中需要完成的救援任务集合，其中Tg表示第g项救援任务，如在地震应急救援中的现场抢救任务、卫生防疫任务等，每项救援任务都需要一个救援小组来完成。

G={Gg|g=1,2,…,m}：所有救援小组集合，其中Gg表示针对救援任务Tg的救援小组，是负责完成任务Tg的救援人员集合。若救援人员Pi被指派去完成任务Tg，则Pi∈Gg；否则，Pi∉Gg。

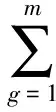
DM={Dg|g=1,2,…,m}：各救援小组中所有救援人员的下标集合，其中Dg表示针对救援任务Tg的救援小组Gg中的各救援人员的下标集合，如果Pi∈Gg，则i∈Dg，i=1,2,…,n，g=1,2,…,m，且满足每个救援人员只能被指派到一个救援小组中，每个救援小组至少包含一个人。

A={Aj|j=1,2,…,l}：完成救援任务所要求的救援人员协同特征评价指标集合，其中Aj表示第j项协同特征评价指标。救援人员的协同特征评价指标用于刻画和度量该救援人员的协作能力，一般可分为“效益型”指标和“成本型”指标两类。其中，效益型指标取值越大，表示救援人员的协作能力越强；其取值越小，表示救援人员的协作能力越弱，如沟通理解力、领导力等[5,6]。成本型指标取值越大，表示救援人员的协作能力越弱，其取值越小，表示救援人员的协作能力越强，如冲突次数[12]、创伤后应激障碍(PTSD)、焦虑症等[13]。

AP=[aij]n×l：救援人员协同特征评价矩阵，其中，aij表示救援人员Pi针对协同特征评价指标Aj的表现值，可以通过调查问卷、历史信息或专家评价获得，i=1,2,…,n，j=1,2,…,l。

B={Bk|k=1,2,…,q}：完成救援任务所要求的救援人员技能特征评价指标集合，其中Bk表示第k项技能特征评价指标。救援人员的技能特征评价指标用于刻画和度量该救援人员的专业技能水平，如医护人员的检伤分诊能力、护理能力和疾病预防能力[14]。B一般可分为“效益型”指标和“成本型”指标两类。其中，效益型指标取值越大，表示救援人员的专业技能越强；其取值越小，表示救援人员的专业技能越弱。成本型指标取值越大，表示救援人员的专业技能越弱；其取值越小，表示救援人员的专业技能越强。

BP=[bik]n×q：救援人员技能特征评价矩阵，其中，bik表示救援人员Pi针对技能特征评价指标Bk的表现值，可以通过调查问卷、历史信息或专家评价获得，i=1,2,…,n，k=1,2,…,q。

BM={Bg|g=1,2,…,m}：各项救援任务所需要的救援人员技能特征评价指标集的集合。由于各项救援任务的性质和内容不同，因此不同的救援任务所需要的救援人员技能也有所不同。其中，Bg表示针对救援任务Tg的评价指标集合，Bg⊂B，且B1∪B2∪…∪Bm=B。例如，在地震应急救援中的现场抢救任务需要救援人员具有良好的护理救援基本技能、检伤分诊能力等，而灾害防疫任务更强调救援人员的疾病预防能力等[14]。

HM={Hg|g=1,2,…,m}：各项救援任务所需要的救援人员技能特征评价指标集的下标集合，其中Hg表示指标集Bg中的各项评价指标的下标集合，如果Bk∈Bg，则k∈Hg，k=1,2,…,q，g=1,2,…,m，且满足H1∪H2∪…∪Hm={1,2,…,q}，Hg≠Ø。

2 救援小组协同度模型

Bardach认为人员间协同合作比个体独立工作能够创造更大的价值[5]。因此假设救援人员在应急救援过程中目标一致，相互间积极协作，相互配合，所产生的协同效应对救援任务的完成起到积极的正向作用。救援小组可被视为一个由救援人员组成的复合系统，而救援小组协同度用来度量小组内救援人员间的协同效应，亦可看作为组内救援人员的协同系数。一般而言，复合系统的不协同是绝对的，协同是相对的，任何一个复合系统总是处在理想协同状态与绝对不协同状态之间的某一状态[9]，协同度实际上是一个相对值，反映并取决于系统实际状态与理想协同状态之间的距离[8]，且协同具有“放大”效应[11]。因此，本文提出了基于欧氏距离平方的协同度模型。

2.1 协同特征评价矩阵的规范化处理

设Aa和Ab分别为效益型指标集合和成本型指标集合，则有Aa∪Ab=A，Aa∩Ab=Ø。若令Oa和Ob分别表示集合Aa和Ab中各指标的下标集合，则有Oa∪Ob={1,2,…,l}，Oa∩Ob=Ø。

依据救援人员协同特征评价矩阵AP=[aij]n×l，将各救援人员在同一指标下的协同评价信息进行规范化处理后得到规范化协同评价矩阵E=[eij]n×l。其中，eij的计算公式如下。

2.2 救援人员的有序度

救援人员的有序度综合评价了该救援人员在相关协同特征指标下的协作能力，用来描述该救援人员与小组内其他成员共同完成救援任务的协调程度。从总体上看，救援人员对救援小组井然有序、和谐一致(即协同效应)的“贡献”可通过救援人员有序度μi来体现。μi取值越大，说明该救援人员能够更好得与小组内其它成员协作，从而使“1+1>2”的协同效应越明显，救援任务完成的更快、效果更好，即促进救援小组的实际效能提高，因此也意味着救援人员对救援小组有序的“贡献”越大。

救援人员有序度μi是eij的函数。eij的取值越大，该救援人员有序度越高，eij的取值越小，该救援人员有序度越低[15]。本文采用线性加权和法定义救援人员有序度，如公式(2)所示。

(2)

由定义可知，μi∈[0,1]，式中ωj为各个协同特征评价指标的权重，可以由专家打分或者AHP法等方法求得。

根据基于距离协同度模型的计算思想[8]，结合本文应急管理背景，分别设定一个救援人员的正理想有序度和负理想有序度，便于后续计算使用。救援人员的正理想有序度表示在理想状态下，该救援人员的各项协同特征指标取值都为最佳，即其协作能力最强。救援人员的负理想有序度表示在理想状态下，该救援人员的各项协同指标取值都为最差，即其协作能力最弱。

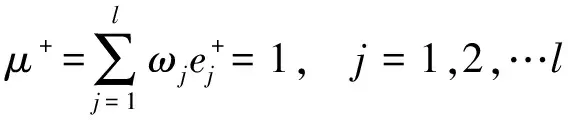
(3a)

(3b)

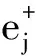
2.3 救援小组的协同状态

设定某一救援小组的正理想协同状态表示在理想状态下，该救援小组中每个成员的有序度都为正理想有序度。救援小组的负理想协同状态表示在理想状态下，该救援小组中每个成员的有序度都为负理想有序度。则救援小组的实际状态、正负理想协同状态可定义如下。

Vg:救援小组Gg的实际状态，Vg={μi|i∈Dg}，g=1,2,…,m。

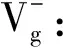
2.4 协同度模型

(4)

(5)

进一步地，根据公式(4)和(5)，救援小组Gg的协同度定义如公式(6)所示。

(6)

由其定义可知，cg∈[0,1]，其值越大，救援小组的有序程序越高，越协同，反之则有序度越低，越不协同。上述所提出的基于欧氏距离平方的协同度模型，具有意义直观、计算简便等特点，能较为有效、直接地反映出实际状态与理想协同状态的距离，体现出协同的本质意义和“放大”效应。

3 考虑协同效应的救援人员分组模型

首先，计算救援人员针对不同救援任务的基础效能。然后，基于上文所提出的协同度模型，构建救援人员实际效能表达式。进而，构建基于实际效能的救援人员分组模型。最后对模型进行变换求解。

3.1 救援人员基础效能的计算

首先，依据救援人员技能特征评价矩阵BP=[bik]n×q，将各救援人员在同一指标下的评价信息进行规范化处理后得到规范化评价矩阵F=[fik]n×q。考虑救援人员技能特征评价指标集B={Bk|k=1,2,…,q}亦可分为“效益型”和“成本型”两类指标，其规范化计算同公式(1)，由于篇幅有限，此处不再赘述。

3.2 基于协同度的救援人员分组模型与求解

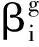
(7)

则基于救援人员实际效能的人员分组模型构建如式(8)所示。

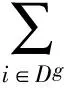
进一步地，采用线性加权和法将上述多目标优化模型转化为单目标优化模型，如式(9)所示。其中，λg表示模型(8)中第g个目标的权数。

(9)

可以看出，模型(9)是一个单目标0-1二次规划问题，这类优化问题已被证明了是NP-hard问题。对于实际的人员分组问题，若人员数量(即决策变量个数)不是很大时，可以依据文献[17,18]，将上述问题转化为0-1线性规划问题来进行求解，其转化过程阐述如下。

(10)

(11)

则模型(9)可转换为如下0-1线性规划问题，进而求其最优解。

(12)

综上所述，基于协同效应的救援人员分组问题的建模与求解步骤如下。

步骤1 根据公式(1)，计算救援人员的规范化协同特征评价矩阵E。

步骤2 根据公式(1)，计算救援人员的规范化技能特征评价矩阵F，并计算救援人员针对不同救援任务的规范化基础效能矩阵R。

步骤3 根据公式(2)和(3)，计算救援人员有序度μi、正理想有序度μ+和负理想有序度μ-。

步骤5 根据公式(12)，构建考虑协同效应的救援人员最优分组问题的数学模型并求解。

步骤6 依据求解结果，确定救援人员的最优分组方案。

4 算例与分析

4.1 算例

[1]，以地震突发事件的应急医护救援为背景，通过一个算例分析来说明本文所提出的分组方法。假设某一地区发生了地震灾害，某一时间段内需要完成三项应急医护救援任务，即：

(1)现场抢救任务(T1)。要求医护人员对从废墟中解救出来的伤员实施第一时间紧急医疗抢救。

(2)一线救援任务(T2)。要求医护人员在临时安置医疗点对伤员进行救援治疗任务。

(3)卫生防疫任务(T3)。要求医护人员在地震灾区进行环境消毒、卫生知识宣传和预防性给药等工作。

基于任务需求，制定应急救援医护人员的协同特征评价指标为：沟通协调能力(A1)、历史上相关经验(A2)、团队精神(A3)、可信任度(A4)和理解力(A5)[5,6]。

制定应急救援医护人员的技能特征评价指标为：检伤分诊能力(B1)、护理救援基本技能(B2)、注重疾病的预防能力(B3)、掌握灾害应急预案知识水平(B4)和独立思考能力(B5)[14]。

假设有13位应急救援医护人员(P1,P2,…,P13)可供选择，且各应急医护救援任务的人员需求量分别为：d1=5，d2=4，d3=2。采用1-5分对每个医护人员进行各指标表现的评价，分值越高则表示医护人员的表现越好，相关基础数据如表1、表2和表3所示。其中，表1和表2中的数据可通过历史信息、专家评价或者在分组前对救援人员进行简短问卷调查获得。文献[5]中整理了一些有关应急协同的影响因素，文献[19]给出了关于交流和信任因素的测度方法。

表1 应急救援医护人员的协同特征评价结果

表2 应急救援医护人员的技能特征评价结果

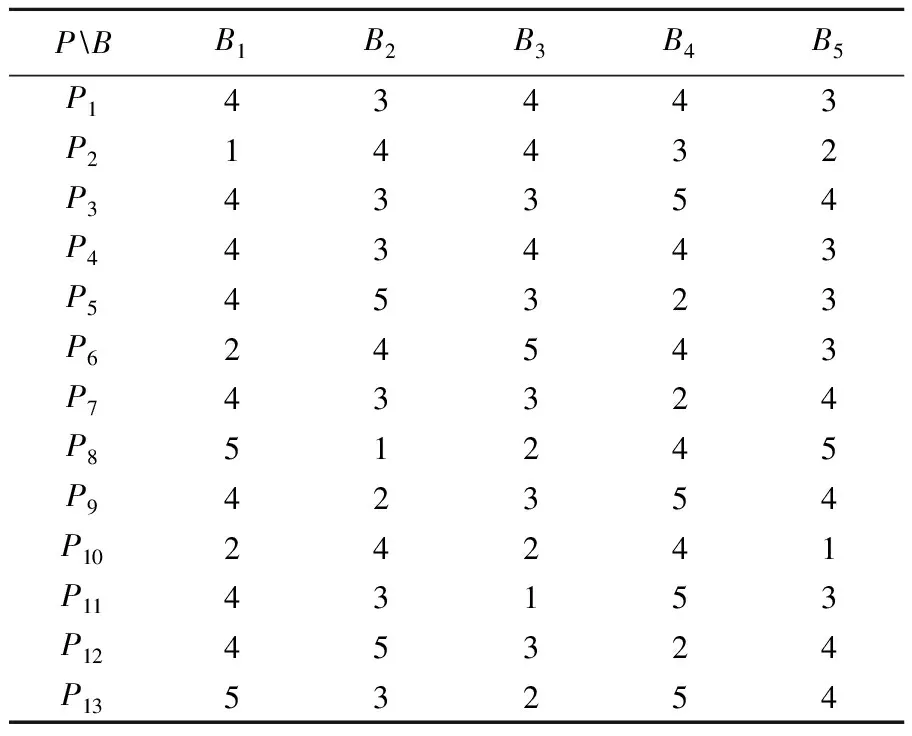
PBB1B2B3B4B5P143443P214432P343354P443443P545323P624543P743324P851245P942354P1024241P1143153P1245324P1353254

表3 各项医护救援任务所需考虑的基础效能评价指标以及指标权重

基于此情景的应急救援医护人员分组的部分计算过程和结果如下。

(1)根据步骤1，计算规范化协同特征评价矩阵E。

(2)根据步骤2，计算规范化技能特征评价矩阵F和救援人员针对不同救援任务的规范化基础效能矩阵R，结果如下。

(3)计算救援人员有序度，取ω1=ω2=…=ω5=0.2，结果如表4所示，且正理想有序度μ+=1，负理想有序度μ-=0。

表4 救援人员有序度

(4)将(μt-μ+)2，t=1,2,…,13，由小到大进行排序，结果为：0.04，0.0625，0.09，0.1225，0.1225，0.16，0.16，0.2025，0.2025，0.3025，0.36，0.36，0.49。经计算，Lg和Ug的取值为：L1=0.4375，U1=1.715，L2=0.315，U2=1.5125，L3=0.1025，U3=0.85。

(5)基于上述计算结果和模型(12)，不失一般性，令λ1=λ2=λ3=1/3，构建针对此算例的考虑协同效应的救援人员分组的数学模型，并通过LINGO软件包进行求解，得到该问题最优解为Y*。

(6)由Y*可知，本例的最优分组方案为：救援人员P5、P7、P8、P11和P12被分配到组完成任务T1；救援人员P1、P3、P9和P13被分配到G2组完成任务；救援人员P2和P6被分配到G3组完成任务；而P4，P10暂时没有被分配任务。

另外，做了两组对比实验。对比实验一：当不考虑协同效应，仅根据救援人员的基础效能分组时，求得最优解为Y′。对比实验二：当考虑协同效应，且救援人员有序度都相同时，采用本文所提出的分组方法求得最优解为Y″。

4.2 分析

通过实验结果Y′与Y″的对比分析可知，二者相同，其主要原因如下。当考虑协同效应，且所有救援人员有序度μi均相同时，即μ1=μ2=…μ13，由公式(6)可知，各救援小组协同度均相同，即c1=c2=c3，因为各救援人员的实际效能同比例变化，所以这两组实验的最优解Y′与Y″相同。进一步地，上述分析可推广到一般情况，即当考虑协同效应，且所有救援人员有序度均相同时，其最优分组方案与不考虑协同效应只考虑救援人员基础效能时的结果相同。

通过实验结果Y′与Y*的对比分析可知，当考虑协同效应时，Y′中G1组的救援人员P13被P11替换，G2组的救援人员P4被P13替换，G3组没有变化。按照Y*中的分组结果，各救援小组协同度分别为：c1=0.8065，c2=0.7844，c3=0.8375。按照Y′中的分组结果，如果考虑本事例中协同指标数据带来的协同效应，那么，各救援小组协同度分别为：c1=0.721，c2=0.8169，c3=0.8375。各救援小组实际效能如表5所示。

表5 救援小组实际效能对比表

(1)针对任务T1，当不考虑协同效应时，P5、P7、P8、P12和P13被分在G1组，当考虑协同效应时，P5、P7、P8、P12和P11被分在G1组。针对这6个人进行分析可得，基础效能r12>r5>r13>r7>r8>r11，有序度μ12>μ11>μ8>μ7>μ5>μ13。由于救援人员在不同的组中或与不同人员合作时，协同度可能会有所不同，救援人员的实际效能也因分组情况不同而不断变化。P5、P7、P8、P12与P13合作时，5人的实际效能之和为6.1956；与P11合作时，5人的实际效能之和为6.2324。对比于Y′，Y*中G1组的协同度提高了11.86%，实际效能提高了0.59%。虽然P13的基础效能优于P11，但P11的有序度优于P13。综合考虑基础效能和协同效应时，Y′中G1组的P13被P11替换。由此可知，协同效应在人员分组中具有重要作用，团队整体协同一致比团队中个人能力更重要，好的协同可以提高小组的整体效能。

(2)针对任务T2，当不考虑协同效应时，P1、P3、P9和P4被分在G2组，当考虑协同效应时，P1、P3、P9和P13被分在G2组。针对这5个人进行分析可得，基础效能r13>r3>r1=r4>r9，有序度μ1>μ9>μ3>μ4>μ13。P1、P3、P9与P4合作时，4人的实际效能之和为4.3605；与P13合作时，4人的实际效能之和为4.4163，小组协同度降低了3.98%，但实际效能提高了1.28%。虽然P4在有序度上优于P13，但在基础效能上P13优于P4，综合考虑基础效能和协同效应时，Y′中G2组P4被P13替换。此外，通过救援人员针对不同救援任务的规范化基础效能矩阵R可知，救援人员P1和P4的基础效能相同；当不考虑协同效应时，P1和P4被分到G2组，而当考虑协同效应时，P1不变，P4由于协同差，影响其基础效能的发挥和小组整体实际效能，没有被分配任务。由此可知，当救援人员基础效能相同时，救援人员有序度越高，协同效应越大，团队协作越好，任务完成“效果”越好。

(3)综上所述，救援人员的实际效能是随着分组情况的变化而变化的，在进行应急救援人员分组时，应综合考虑救援人员的实际效能和协同效应，从全局出发，使得救援小组整体的总实际效能最大，以达到所有救援任务总体完成“效果”最好的目的。

5 结束语

考虑人员间协同效应的救援人员分组是应急管理领域中的一个热点和难点问题。本文基于系统协同理论思想，引入了协同度概念，所提出的救援小组协同度模型可定量化度量协同效应。并以此为基础，在救援人员实际效能分组前不确定的情况下，建立人员分组优化模型，并将该多目标0-1二次规划问题转化为单目标0-1线性规划问题进行求解，从而完成人员分组，弥补了以往传统指派问题没有考虑协同效应的局限性，为进一步解决救援人员分组问题提供了新的思路和方法。该方法综合考虑了救援人员的基础效能和协同效应，且逻辑清晰、计算简单，具有较强的可操作性和实用性。在未来的研究工作中，将进一步深入探讨针对具有偏序关系的多个救援任务的救援人员动态分组模型及其求解方法。

参考文献：

[1] 樊治平,刘洋,袁媛,朱少华.突发事件应急救援人员的分组方法研究[J].运筹与管理,2012,21(2):1-7.

[2] 袁媛,樊治平,刘洋.突发事件应急救援人员的派遣模型研究[J].中国管理科学,2013,21(2):152-160.

[3] 刘奕,周琦,苏国锋,刘轩,刘乐民.基于Multi-Agent的突发事件多部门协同应对建模与分析[J].清华大学学报(自然科学版),2010,50(2):165-169.

[4] 陈兴,王勇,吴凌云,闫桂英,朱伟.多阶段多目标多部门应急决策模型[J].系统工程理论与实践,2010,30(11):1977-1985.

[5] Naim Kapucu, Tolga Arslan, Fatih Demiroz. Collaborative emergency management and national emergency management network[J]. Disaster Prevention and Management, 2010, 19(4): 452- 468.

[6] Chen Rui, Raj Sharman, Rao H Raghav, Shambu J Upadhyaya. Coordination in emergency response management[J]. Communications of ACM, 2008, 51(5): 66-73.

[7] Liaquat Hossain, Shahadat Uddin. Design patterns: coordination in complex and dynamic environments[J]. Disaster Prevention and Management, 2012, 21(3): 336-350.

[8] 汤铃,李建平,余乐安,覃东海.基于距离协调度模型的系统协调发展定量评价方法[J].系统工程理论与实践,2010,30(4):594- 602.

[9] 白华,韩文秀.复合系统及其协调的一般理论[J].运筹与管理,2000,9(3):1-7.

[10] 阮旻智,李庆民,于志良,王红军.基于多阶段多指标的编队干扰方案协同决策研究[J].系统工程与电子技术,2009,31(6):1404-1408.

[11] 卜先锦.指控单元战术协同效果分析、建模与应用[D].湖南:国防科学技术大学,2006.

[12] 谢心灵.团队协同的知识工作效率影响因素及效率评价研究[D].四川:重庆大学,2010.

[13] 任清涛.突发灾难事件中现场救援人员心理危机干预的前瞻性研究[D].山东:山东大学,2009.

[14] 黄叶莉,李书梅,王玚,蔡伟萍.文献回顾分析法总结灾害救援中的护理能力[J].解放军护理杂志,2012,29(10A):20-23.

[15] 孟庆松,韩文秀.复合系统协调度模型研究[J].天津大学学报,2000,33(4):444- 446.

[16] 王红军,迟忠先.编队干扰方案协同决策研究[J].系统工程理论与实践,2007,27(4):171-176.

[17] Glover F. Improved linear integer programming formulations of nonlinear problem[J]. Management Science, 1975, 22(4): 455- 460.

[18] 冯博,樊治平,付娜.一种基于协同信息的团队伙伴选择方法[J].运筹与管理,2007,16(5):58- 61.

[19] Saonee Sarker, Manju Ahuja, Suprateek Sarker, Sarah Kirkerby. The role of communication and trust in global virtual teams: a social network perspective[J]. Journal of Management Information Systems, 2011, 28(1): 273-309.

Grouping Method of Rescuers in Emergency Rescue Considering the Synergistic Effect

YE Xin, WANG Xue, ZHONG Qiu-yan

(SchoolofManagementScienceandEngineering,DalianUniversityofTechnology,Dalian116024,China)

A grouping method of rescuers considering synergistic effect is proposed to solve rescuers grouping problem in the emergency management. Firstly, a description of the grouping problem of emergency rescuers is presented. Then, in order to quantify synergistic effect among rescuers, a synergetic degree model of rescue group based on system synergy theory is proposed. Furthermore, the basic efficiency of rescuers and the synergistic effect among rescuers are considered comprehensively. Base on synergetic degree model, the actual efficiency expression of the rescuers to complete different tasks is proposed. On this basis, the rescuers grouping optimization model is constructed, in which the objectives are to maximize the actual efficiency of each rescue group. This model belongs to the multi-objective 0-1 quadratic integer programming model. Furthermore, the procedure of converting this multi-objective 0-1 quadratic integer programming model into single-objective 0-1 linear integer programming model is presented and then the optimal grouping plan of rescuers can be obtained. Finally, an illustrating example and analysis show the feasibility and effectiveness of the proposed method.

emergency management; rescuer grouping; synergistic effect; optimization model

2013- 08-28

国家自然科学基金重大研究计划重点支持项目(91024029)

叶鑫(1977-)，男，博士，辽宁本溪人，副教授，研究方向：复杂信息系统建模、决策技术、应急管理、电子政务；王雪(1987-)，女，黑龙江鹤岗人，硕士研究生，研究方向：应急管理；仲秋雁(1963-)，女，辽宁沈阳人，教授，研究方向：信息系统、应急管理。

C934,N945

A

1007-3221(2015)01- 0237- 09