突发事件下不对称信息供应链协调机制研究
2015-07-07吴忠和吴晓志解东川
吴忠和, 陈 宏, 吴晓志, 解东川
(1.广东科贸职业学院 管理系,广东 广州 510430; 2.电子科技大学 经济与管理学院,四川 成都 610054)
突发事件下不对称信息供应链协调机制研究
吴忠和1, 陈 宏2, 吴晓志2, 解东川2
(1.广东科贸职业学院 管理系,广东 广州 510430; 2.电子科技大学 经济与管理学院,四川 成都 610054)
针对一个由供应商和一个零售商构成的供应链,在零售商成本为私有信息条件下,假设产品的市场需求为零售价格的指数函数,研究如何协调供应链应对突发事件。首先,给出了对称信息下供应链协调模型;然后,研究了不对称信息下集权式与分权式供应链的协调机制;再次,在突发事件引起零售商成本分布函数扰动情况下,通过引入供应商由于可能需要调整生产计划而产生的偏差成本,研究了供应链的最优应对策略。 研究表明,供应链的最优生产计划、最优批发价格和最优零售价格均具有一定的鲁棒性,当突发事件造成零售商期望成本在一定范围内发生扰动时,三者可以保持不变,当零售商期望成本扰动超过一定范围内时,则需要对之加以调整,才能有效应对突发事件。最后,通过数值仿真验证了相关结论。
不对称信息;供应链;应急管理;协调机制
0 引言
当今突发事件频发的社会环境,充满了许多不确定的因素,供应链运作过程中经常会遇到各种各样的突发情况,如911恐怖袭击、战争、“非典”、“禽流感”等重大公共卫生事件、5.12汶川大地震、3.11日本大地震、4.20芦山大地震等重大自然灾害事件,使得供应链原先制定的计划出现了偏离或者扰动,原来协调的供应链不再协调,影响了供应链上各节点企业的合作,从而影响了整个供应链的竞争力,给企业和供应链管理造成了巨大的影响。企业界和学术界都意识到了突发事件下供应链协调机制的重要性。因此,研究供应链应对突发事件的协调应对策略具有重要的现实意义。
目前,对于突发事件下供应链协调问题的研究正处于起步阶段。Qi等[1]研究了在单供应商和单零售商构成的简单供应链系统中,在假设零售商面对的市场需求是关于价格的线性函数的情形下,当需求出现扰动时,如何利用全单位数量折扣契约应对突发事件,以实现供应链的协调;Xu等[2]运用数量折扣契约研究了在零售商面临指数需求下突发事件导致生产成本发生扰动的二级供应链;Huang等[3]针对指数需求函数情形进行需求扰动的供应链应急协调研究;于辉等[4]假定需求为线性函数,在考虑需求敏感系数变化下,给出了抗突发事件的数量折扣契约;吴忠和等[5,6]研究了二级供应链中突发事件造成市场需求和零售商购买成本同时发生扰动时,以及突发事件造成随机市场需求分布函数和制造商生产成本同时扰动时的供应链应急协调问题,分别采用数量折扣契约和期权契约实现了供应链的协调;此外,吴忠和等[7]在Xiao等[8]研究需求变化下一个供应商和两个基于Bertrand博弈竞争零售商组成的二级供应链对突发事件的协调应对的基础上,进一步研究了生产成本、市场需求和价格敏感系数同时扰动的协调机制,运用线性数量折扣契约实现了多因素扰动下的供应链协调;Chen等[9]运用数量折扣契约研究了需求扰动时一个供应商和一个零售商占主导地位及多个附加零售商组成的供应链;盛方正等[10]考虑了由一个供应商和n个零售商组成的供应链中,在存在突发事件的供应链中使用线形转移支付合同协调供应链的问题,给出了可以协调供应链的转移支付合同应满足的条件。
在非对称信息供应链协调机制研究方面,Yue等[11]利用Bertrand博弈理论研究了市场预测信息为不对称信息时的两个相互补充产品的供应链优化决策;索寒生等[12]研究了在私有信息下,供应商运用委托-代理模型实施了最优回购策略,但信息结构的非对称导致分布式系统的决策偏离集权式系统下的决策,因此在非对称信息情况下供应链无法达到协调;徐晓燕等[13]了生产成本信息不对称条件下,当零售商处于主导地位时,供应商的谎报行为以及谎报对供应链绩效的影响。对于信息不对称的供应链协调问题,与这些研究相比,本文的创新点在于构建的是需求与价格之间为负指数函数关系,考虑的是销售成本为零售商的私有信息,通过机制设计实现了分权式系统下的供应链协调。而索寒生等[12]以零售价格为非对称信息,供应商不知道零售价格,只知道其分布,该研究的分布式系统供应链无法实现协调;徐晓燕等[13]的研究以生产成本信息为不对称信息,也无法实现分散式供应链的协调。
目前,有关非对称信息下供应链应急管理方面的研究还很少涉及。覃艳华等[14]考虑了二级供应链在随机市场需求下突发事件导致市场需求发生变化且变化后的需求信息是不对称信息时的供应链协调问题;曹细玉等[15]考虑了机市场需求下的二级供应链,探讨了突发事件导致市场需求和零售商边际成本同时变化且变化后的零售商边际成本是不对称信息时回购契约对供应链的协调作用。
与一般的对称信息或不对称信息供应链协调问题相比,突发事件下的不对称信息供应链协调问题的技术难点在于,既要通过机制设计,设法消除信息不对称的障碍,使信息共享,以使供应链获得最大效率,又要设法克服突发事件对供应链参数扰动的影响,寻求应对突发事件引起供应链参数扰动的协调策略。
本文针对一个由供应商和一个零售商构成的二级供应链,假设产品的市场需求为零售价格的指数函数,在零售商成本为私有信息条件下,在面对突发事件引起的零售商生产成本变化的情况下,研究如何调整原来的生产计划来实现供应链的协调。
1 对称信息下供应链最优决策

首先考虑集权供应链的情况,在集权式供应链中,由集中决策者来寻求供应链整体的最大化。
供应链系统的利润为:

最优订货量:q*=ae-(1+k(cs+cr))
2 不对称信息下的供应链协调机制

(1)集权式控制情形
在集权式控制下,供应链系统由一个决策者统一作出决策,集权式控制下供应链期望利润模型为:
Πc(p)=E[q(p-cs-cr)]

结论1 集权式控制下供应链最优契约为:
(1)
最优订货量为:qc=ae-(1+k(cs+μ))
(2)
(3)
(2)分权式控制情形
在分权式控制下,供应链成员是以追求自身利润最大化为目标的独立决策者。根据委托一代理理论,供应商是委托人,零售商是代理人。这是一个逆向选择问题,在签订契约之前,供应商不知道零售商的成本信息,根据机制设计原理,供应商首先提出契约,零售商决定是否接受,如果接受契约,则选择订单数量和零售价来最大化其期望利润。除了零售商成本信息外,其他参数都是博弈参与人的共同知识。
对于供应商来说,其优化问题就是最大化其期望利润,目标函数可表示为:
供应商优化问题可表示为:
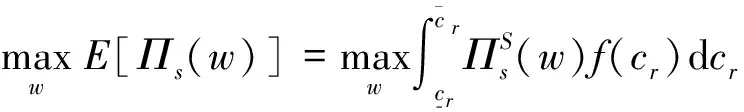
(4)
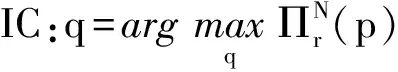
(5)
式(5)表示零售商的激励相容IC约束,零售商选择q最大化自己的利润。式(4)表明供应商的期望利润取决于零售商由式(5)激励相容约束条件得到的订货量q。
1)零售商的优化问题
零售商的期望利润函数可写成:
Πr(p)=q(p-w-cr)=ae-kp(p-w-cr)
(6)
相应的最优订货量为:
q(w)=ae-(1+k(w+cr))
(7)
2)供应商的优化问题
结论2 分权式控制下,无突发事件时在不对称信息下的供应链协调契约为:
最优批发价格为:
(8)
最优零售价格为:
(9)
最优订货量为:
qN=ae-(2+k(cs+μ))
(10)
相应地,零售商的期望利润为:
(11)
供应商的期望利润为:
(12)
供应链系统的期望利润为:
(13)
3 突发事件下不对称信息供应链协调机制
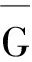
当零售商成本发生变化后,供应链系统对原来的生产计划的调整会引起额外的费用。因此,供应链应急管理的决策模型中应考虑这些偏差费用。设突发事件下供应商优化问题可表示为:
目标函数:
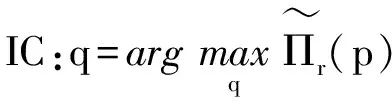
考虑改变生产计划引起的偏差费,用则供应商的利润函数为:
(14)
假设突发事件发生后,零售商的最优订货量为qD,当新的订货量qD>qN时,由于打破了原有生产计划,对于增加的产品qD-qN,需要增加新的生产成本λ1;而如果突发事件导致订货量比原有生产计划量qN少,对于剩余的产品qN-qD,将招致新的处理费用λ2,(x)+=max(0,x)。
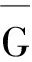
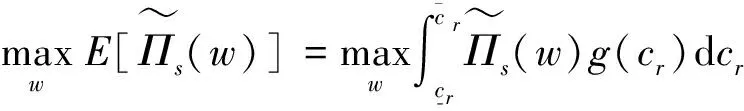
(15)
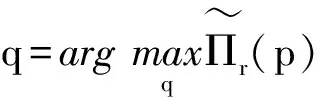
(16)
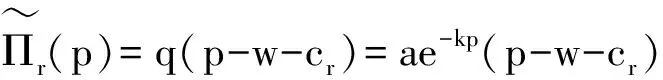
最优零售价格为:
(17)
相应最优订货量为:
q(w)=ae-(1+k(w+cr))
(18)
下面考虑两种情形时供应链的协调机制。
供应商的优化问题就可表示为:
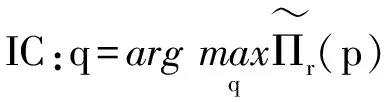
零售商的期望利润为:
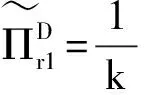
供应商的期望利润为:
供应链系统的期望利润为:
供应商的优化问题就可表示为:
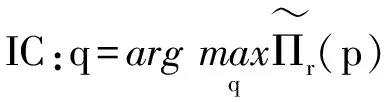
供应链系统的期望利润为:
总结上面的结果,可得到下面的定理1。
定理1 突发事件下不对称信息供应链协调机制为:
最优订货量为:
最优的零售价格为:
最优的批发价格为:
零售商的期望利润为:
供应商的期望利润为:
供应链系统的期望利润为:
由定理3,可以得出以下结论:突发事件下的原生产计划具有很强的鲁棒性。当突发事件造成零售商成本在[μ-λ1,μ+λ2]范围内扰动时,供应链的原有生产计划科保持不变,原有的协调机制可以实现供应链的协调;当突发事件造成零售商的成本扰动超出[μ-λ1,μ+λ2]范围时,需要对原协调策略加以调整,才能使供应链重新达到协调,实现最优利润。
4 算例分析
本部分通过具体的算例分析来验证文中建立的模型。
假设a=8000,k=0.5,cs=5,λ1=0.3,λ2=0.2,零售商的成本分布函数F(cr)是均匀分布且μ=2,突发事件可能引起零售商成本的增加或减少,假设突发事件造成零售商成本的期望值扰动范围为[1,3]。
4.1 不对称信息下突发事件时零售商的成本扰动对供应链的影响
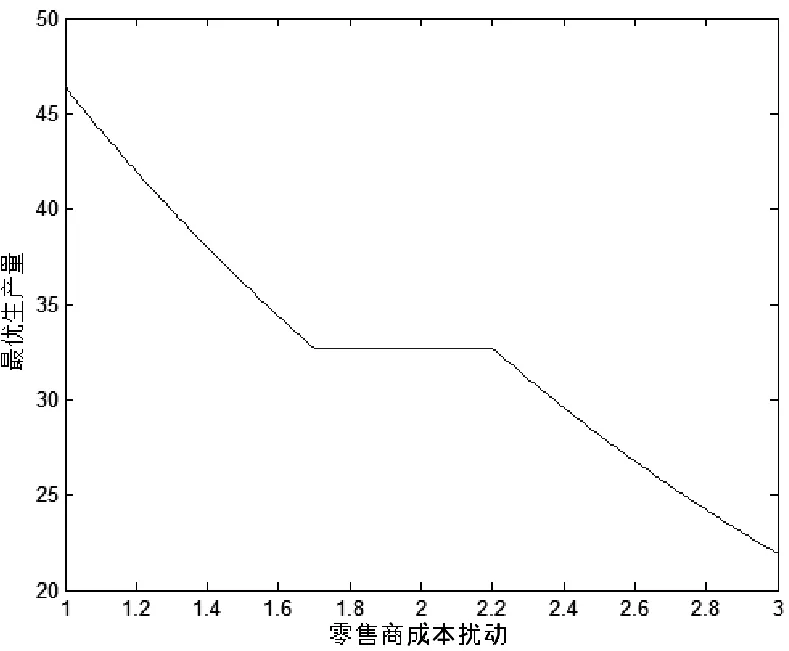
图1 μG与最优生产量的关系
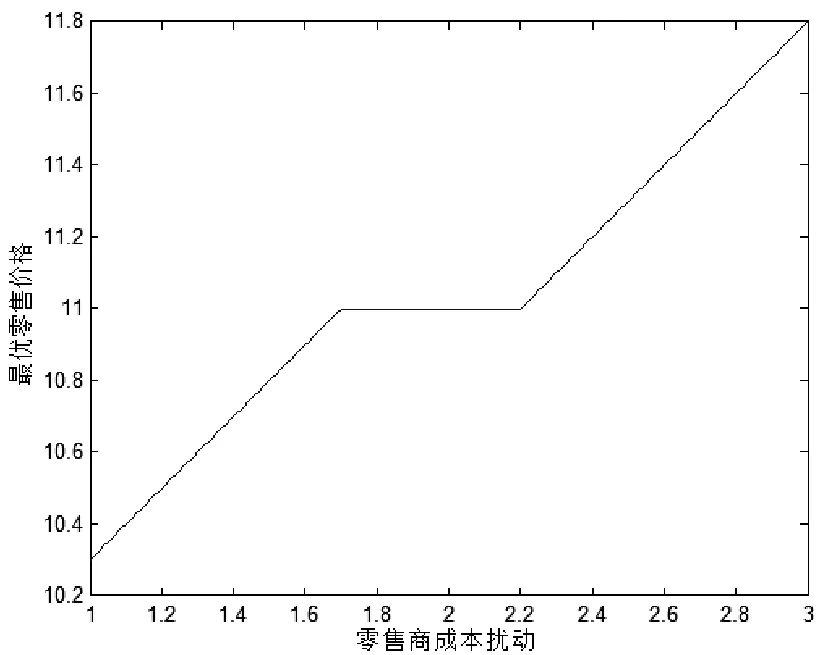
图2 μG与最优零售价格的关系

图3 μG与最优批发价格的关系
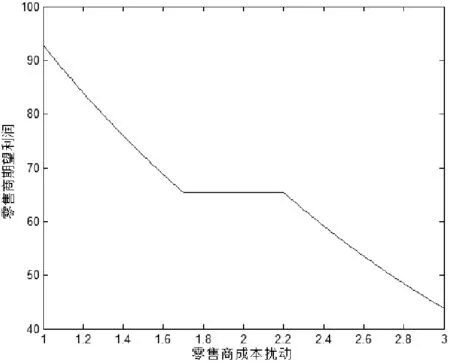
图4 μG与零售商期望利润的关系
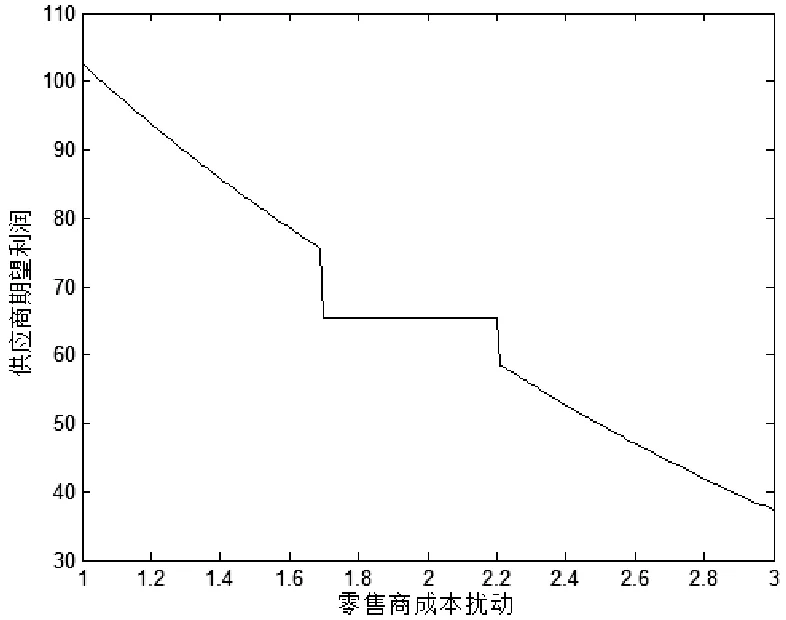
图5 μG与供应商期望利润的关系
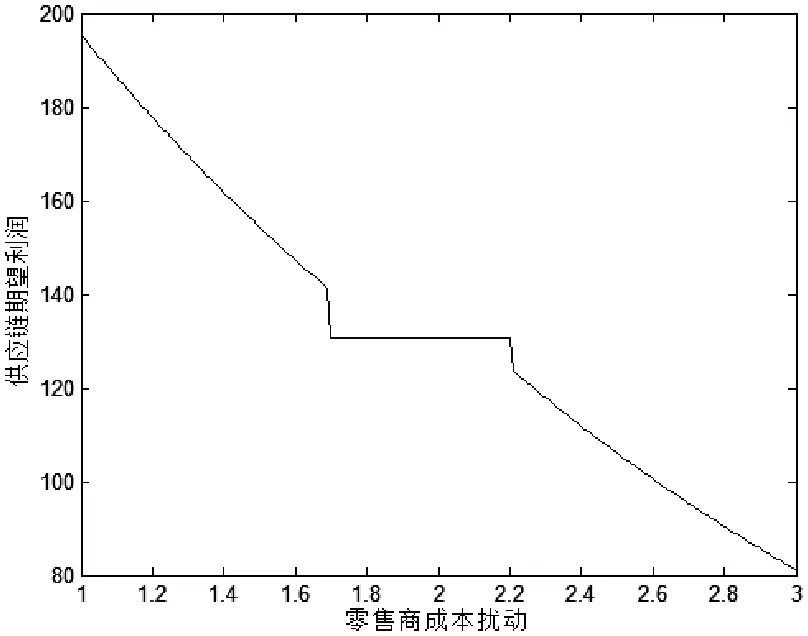
图6 μG与供应链期望利润的关系
从上图可以看出,突发事件发生后:
(1)零售商成本扰动对最优生产量的影响
当μG<μ-λ1时,最优生产量随着μG非线性递减,大于无突发事件发生时的生产量,即qD>qN;当μG>μ+λ2时,最优生产量随着μG非线性递减,小于无突发事件发生时的生产量,即qD (2)零售商成本扰动对最优零售价格的影响 当μG<μ-λ1时,最优零售价格随着μG线性递增,小于无突发事件发生时的零售价格,即qD (3)零售商成本扰动对最优批发价格的影响 最优批发价格在μG扰动的各区域不随μG扰动发生变化。当μG<μ-λ1时,最优批发价格大于无突发事件发生时的批发价格,即wD>wN;当μG>μ+λ2时,最优批发价格小于无突发事件发生时的批发价格,即wD (4)零售商成本扰动对最优期望利润的影响 4.2 不对称信息下突发事件时需求价格弹性对供应链的影响 表1 不对称信息下突发事件时需求价格弹性对供应链的影响 从表1可以看出,在不对称信息下,当突发事件引起零售商成本降低,进而导致市场需求增加时,随着需求价格弹性的增大,供应商批发价格、零售商零售价格、最优订货链及供应链成员期望利润均是逐步减少的,从而,供应链系统的最优期望利润也是逐步减少的。 突发事件下的供应链协调机制已成为非常重要的课题。本文研究了非对称信息下发生突发事件的供应链协调机制。根据以上分析,可以得出以下结论:(1)如果突发事件造成零售商成本扰动很小,没有超过阈值,那么供应链的最优应对策略就是保持原来的生产计划不变,可以保证系统的正常运行。(2)如果突发事件造成零售商成本扰动范围较大,超过了阈值,必须对原来的生产计划、批发价格和零售价格作出调整,才能实现供应链的协调。 本文的研究仅是考虑一个博弈双方均为风险中性的二级供应链对突发事件的协调应对,但是实践中,一对多的二级供应链或三级供应链更为常见,因此,考虑非对称信息下一对多或多级的更加复杂结构且博弈方具有风险偏好的供应链的应急协调,将是进一步的研究方向。 [1] Qi X T, Bard J, Yu G. Supply chain coordination with demand disruptions[J]. Omega, 2004, 32(4): 301-312. [2] Xu M H, Qi X T, Yu G, et al. Coordinating dyadic supply chains when production costs are disrupted[J]. IIE Transaction, 2006, 38(9): 765-775. [3] Huang C C, Yu G, Wang S, et al. Disruption management for supply chain coordination with exponential demand function[J]. Acta Mathematica Scientia, 2006, B26(4): 655- 669. [4] 于辉,陈剑,于刚.协调供应链如何应对突发事件[J].系统工程理论与实践,2005,25(7):9-16. [5] 吴忠和,陈宏,赵千,吴晓志.需求和零售商购买成本同时扰动的供应链应急协调[J].中国管理科学,2012,20(6):110-117. [6] 吴忠和,陈宏,赵千.需求和生产成本同时扰动下供应链期权契约应对突发事件[J].中国管理科学,2013,21(4):9-104. [7] 吴忠和,陈宏,赵千,吴晓志.两零售商竞争下多因素同时扰动的供应链协调研究[J].中国管理科学,2012,20(2):62- 67. [8] Xiao T J, Qi X T, Yu G. Coordination of supply chain after demand disruptions when retailers compete[J]. International Journal of Production Economics, 2007, 109: 162-179. [9] Chen K B, Xiao T J. Demand disruption and coordination of the supply chain with a dominant retailer[J]. European Journal of Operational Research, 2009, 197(1): 225-234. [10] 盛方正,季建华,周娜.多个零售商情况下使用转移支付协调发生突发事件的供应链[J].管理工程学报,2009,23(1): 76- 81. [11] Yue X H, Mukhopadhyay S K, Zhu X W. A bertrand model of pricing of complementary goods under information asymmetry[J]. Journal of Business Research, 2006, 59(10/11): 1182-1192. [12] 索寒生,金以慧.非对称信息下供需链中供应商的回购策略分析[J].控制与决策.2004,19(3): 335-338 [13] 徐晓燕,吴三平.生产成本信息不对称得两级供应链协调研究[J].系统工程学报,2009,24(1): 18-24 [14] 覃艳华,曹细玉,宋璐君.突发事件下需求信息不对称时的供应链协调应对[J].运筹与管理,2012,21(4):60- 64. [15] 曹细玉,覃艳华.突发事件且非对称信息下的供应链回购契约模型[J].工业工程,2012,15(5):99-104. Supply Chain Coordination Mechanism under Asymmetric Information and Disruptions WU Zhong-he1, CHEN Hong2, WU Xiao-zhi2, XIE Dong-chuan2 (1.SchoolofManagement,GuangdongVocationalofCollegeandTrade,Guangzhou510430,China; 2.SchoolofManagementandEconomics,UniversityofElectronicScienceandTechnologyofChina,Chengdu610054,China) Focusing on a supply chain consisting of a supplier and a retailer, this paper studies how to coordinate the supply chain to respond to the disruption by supposing that the market demand of the product is the exponent function of the price under asymmetric information. Firstly, the coordination model under symmetrical information is given. Secondly, the coordination mechanisms of centralized supply chain and decentralized supply chain are researched. Thirdly, the optimal strategies under the fluctuation of the retailer cost distribution function caused by disruption are studied. The studies show that the optimal product plan, the optimal wholesale price, and the optimal retail price of the supply chain all have some certain robustness. When the expectation retail cost caused by disruption in a scope fluctuates, the three aspects keep unchanging. When the fluctuation of the expectation retail cost exceeds the scope, only the three aspects are adjusted so that the disruptions can be responded efficiently. Finally, through a numerical example some relational conclusions are verified. asymmetric information; supply chain; disruptions management; coordination mechanism 2013- 05-15 国家自然科学基金项目(70773017);2011年度高等学校博士学科点专项科研基金资助课题(博导类)(20110185110022) 吴忠和(1969-),男,广东廉江人,博士,研究方向:供应链管理、博弈论;陈宏(1957-),男,广西苍梧人,教授、博士生导师,研究方向:供应链管理、营销管理。 F406.2 A 1007-3221(2015)01- 0048- 09

5 结论
