奇异协方差阵及不同借贷利率下均值—方差模型的解析解
2015-07-07蒋春福彭泓毅
蒋春福, 彭泓毅
(1.深圳大学 数学与计算科学学院,广东 深圳 518060; 2.华南农业大学 理学院,广东 广州 510642)
奇异协方差阵及不同借贷利率下均值—方差模型的解析解
蒋春福1, 彭泓毅2
(1.深圳大学 数学与计算科学学院,广东 深圳 518060; 2.华南农业大学 理学院,广东 广州 510642)
随着金融资产种类的增加,特别是考虑大规模投资组合问题时,很可能出现资产间的多重共线性或相关性,从而出现协方差阵奇异的情况。然而,目前关于投资组合的均值—方差分析大都是在协方差阵正定的条件下得到的,因此,不适用于奇异协方差阵的情形。针对这一问题,利用广义逆矩阵研究了协方差阵奇异时的均值—方差投资组合模型,在不同借贷利率条件下得到了前沿组合和组合前沿的解析解,突破了传统方法中要求协方差阵可逆的限制,推广了经典Markowitz模型。
金融工程;证券组合;Moore-Penrose广义逆;不同借贷利率
0 引言
对于Markowitz问题的研究,以往的文献大都假定协方差阵为正定,但是随着资产种类的增加和金融衍生产品的大量涌现,这时很可能出现多重共线性和相关性,从而出现协方差阵奇异的情况.此外,当考虑大规模投资组合时,也会出现这样的问题,比如最近Fan[1]的研究.Buser[2]最先研究奇异协方差阵下的投资组合问题,通过技术性地构造两个新的基金得到此时两基金定理仍然成立,Ryan和Lefoll[3]指出文献[2]中的两基金定理的证明过程存在错误,并做了纠.Szegö[4]曾猜想当协方差阵的秩小于n-1时证券市场要么存在套利,要么存在有效子集.此外,还有VöRöS[5]研究了一些具有特殊协方差结构的投资组合问题,Korki和Turtle[6]则是考虑了证券数量趋于无穷大时的极限问题.
我国学者史树中和杨杰[7]指出协方差阵奇异时有可能存在有效子集,还给出了判定证券子集是否为有效子集的充要条件.最近,姚海祥等[8]在无套利假设下分析了奇异协方差阵下证券组合有效前沿的特征,苏咪咪和叶中行[9]则是利用主成分分析方法研究了协方差阵秩为n-1的情形,蒋春福和戴永隆[10]利用矩阵广义逆方法给出了任意秩协方差阵下均值-方差模型的解析解,突破了传统均值-方差分析中要求协方差阵可逆的限制.对于存在不同借贷利率下的证券组合选择额问题,Zhang等[11]在协方差阵正定条件下得到了问题的解析解,本文试图利用矩阵广义逆方法将他们的结果推广到奇异协方差阵的情形。
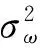
s.t.ω∈D
(1)
其中D={ω∈Rn|ω′μ+(1-ω′1)r(ω)=rp},这里ω为风险证券的投资比例向量,
为无风险证券的收益率函数,这里rb和rl分别为投资者借款和贷款的无风险利率,并且假定rb≥rl.模型(1)不是一个简单的二次规划问题,为求解模型(1)我们先引入如下记号
Dl={ω∈Rn|ω′μ+(1-ω′1)rl=rp,ω′1≤1}
Db={ω∈Rn|ω′μ+(1-ω′1)rb=rp,ω′1>1}
显然,Dl和Db均为凸集,并且我们注意到D=Dl∪Db,Dl∩Db=Ø。根据文献[11]的分析,模型(1)可以分解为如下两个二次规划问题,即存在无风险贷款的均值—方差模型
(2)
和存在无风险借款的均值—方差模型
(3)
一般地,矩阵A的Moore-Penrose广义逆记为A+,由Dunne和Ston[12]不难得到如下的引理.
引理1 设V为n阶非负定矩阵,ρ∈R为任一实数,η=μ-ρ1,T=V+ηη′ ,若η∈M(V),则有
1 模型求解
1.1 存在无风险贷款的情形
为对模型(2)进行求解,可构造Lagrange函数
不难得到Kuhn-Tucker条件如下
(4)
(5)
1-ω′1≥0
(6)
λ1≥0
(7)
λ1(ω′1-1)=0
(8)
根据(7)可对λ1分两种情况讨论
(i)当λ1=0时,令ηl=μ-rl1,则可得矩阵方程
(9)
由文献[10]引理3知,当μ≠rl1时,上述矩阵方程有解。求解该方程可得
(10)
其中T=V+ηlηl′,NT=I-TT+,ξ为任意n维向量.注意到ηl∈M(V),因此由引理1得组合前沿为
(11)
由(10)及引理1可得风险资产投资比例为
(12)
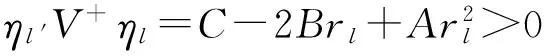
rp(B-rlA)≤C-rlB
(13)
类似于Zhang[11]的分析,下面对B-rlA分三种情况讨论
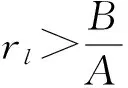
(14)
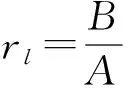
(15)
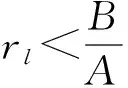
(16)
(ii)当λ1>0时,有等式ω′1=1,因此可得矩阵方程.
(17)
注意到μ∈M(V),1∈M(V)类似文献[11]定理3.3的证明,求解矩阵方程(17)可得到
(18)
注意到D=AC-B2,因此λ1>0等价于
(B-Arl)rp>C-Brl
(19)
同理,根据不等式(19),对B-rlA分如下三种情况讨论
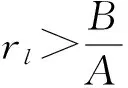
(2)若B-rlA=0,即rl=B/A,则不等式(19)不成立。
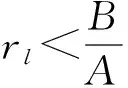
综合上述分析,对于存在无风险贷款的投资组合模型(2),其组合前沿和前沿组合有如下结论:
(1)若B-rlA<0,即rl>B/A,则前沿组合为
组合前沿为
(20)
(2)若B-rlA=0,即rl=B/A,则前沿组合为(15), 组合前沿为
(21)
(3)若B-rlA>0,即rl
组合前沿为
(22)
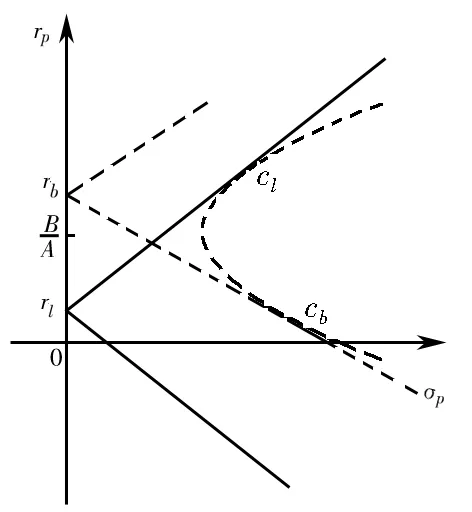
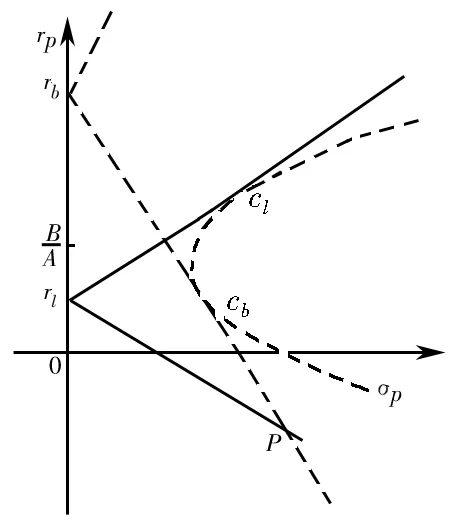
上述三种情形下的组合前沿在(σp,rp)平面上分别如图1、图2和图3所示。

图1 rl>BA的情形
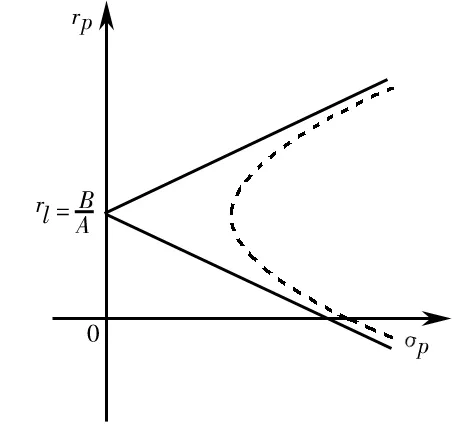
图2 rl=BA的情形
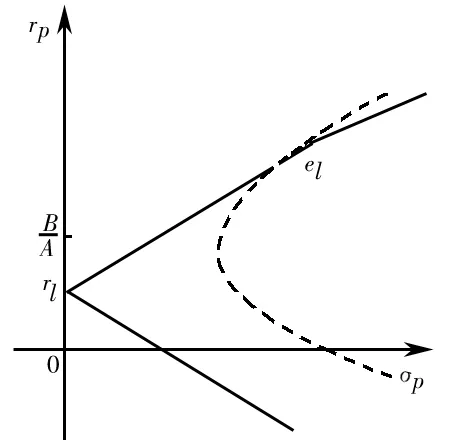
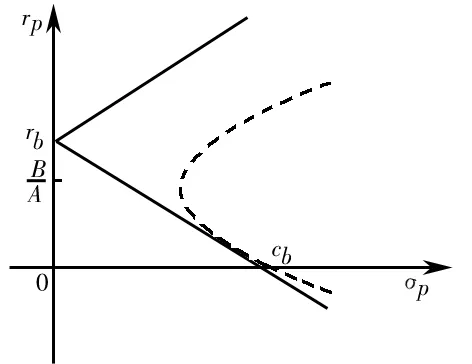
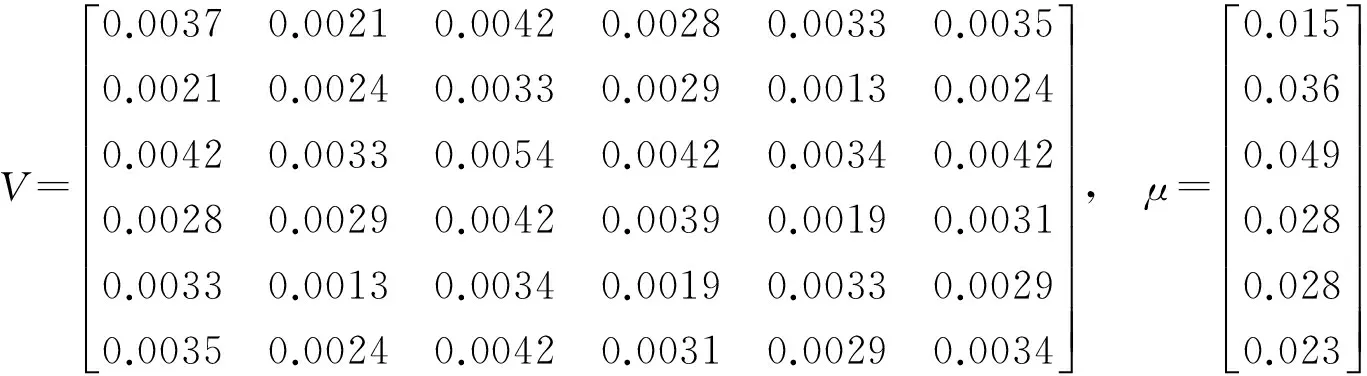
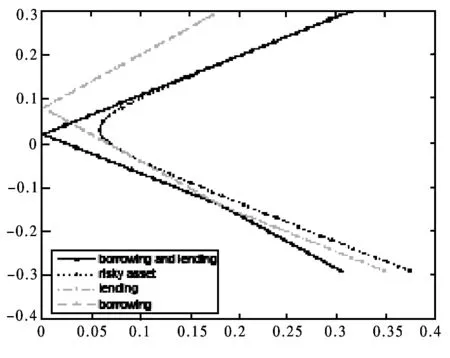
图3 rl 1.2 存在无风险借款的情形 对模型(3)的求解,可构造Lagrange函数 类似地,Kuhn-Tucker条件为 (23) (24) 1-ω′1<0 (25) λ1≤0 (26) λ1(ω′1-1)=0 (27) 由(25)和(27)知λ1=0。由(23)和(24)可得矩阵方程 其中ηb=μ-rb1。类似地,上述矩阵方程的解为 (28) (29) 类似地,对B-rbA分三种情况讨论,便可得到如下的结论: (2)若B-rbA=0,即rb=B/A,此时不等式(29)不成立。 组合前沿在(σp,rp)平面上如图4和图5所示,图中的实线部分为组合前沿,为切点组合。 图4 rb>BA的情形 图5 rb 1.3 存在无风险借贷的情形 根据上述分析,需对模型(2)和模型(3)的组合风险进行比较。类似于文献[11],可分如下几种情况: (1)若B/A 组合前沿为 组合前沿在(σp,rp)平面上分别如图6所示。 (2)若B/A=rl 组合前沿为 组合前沿在(σp,rp)平面上分别如图7所示. (3a)当rb-B/A 组合前沿为 组合前沿为 上述两种情形下的组合前沿在(σp,rp)平面上分别见图8和图9中的实线部分。 (4)若rl 组合前沿为 组合前沿在(σp,rp)平面上如图10中的实线部分。 图8 rb-BA 图9 rb-BA>BA-rl的情形 图10 rl 本节给出一个算例.设rb=0.08,rl=0.02,另有6种风险证券,其协方差阵和期望收益率向量为 利用Matlab可以发现rank(V)=3,因此为奇异阵.计算可得 A=300.03,B=9.29,C=1.04,D=225.22,B/A=0.031 不难验证rb-B/A>B/A-rl,假设目标收益率rp=0.05,那么由2.3节的计算方法,可得如下结果 表1 前沿组合计算结果 这里ei为单位矩阵的第i列,组合前沿及其在(σp,rp)平面上的图形如下所示,图中点实线为组合前沿。 图11 不同借贷利率下证券组合的组合前沿 在投资组合选择模型中,传统的均值-方差分析都是在协方差阵为正定条件下进行的,这在资产种类较少时一般是成立的,但是考虑大规模投资组合或考虑包含衍生产品的投资组合问题时,或者当样本数据的观测区间较短时,那么就可能会出现奇异协方差阵的情形。本文在允许卖空并存在不同借贷利率的条件下得到了前沿组合和组合前沿的解析表示,推广了文献[11]的结果.特别地,当V可逆时本文的结果与文献[11]是一致的。与他们的结果不同的是,当协方差阵奇异时,前沿组合的解不唯一,这是因为在前沿组合的通解中含有可取为任意实数向量的项。尽管如此,组合前沿的解析表示仍然是唯一的,并且其性质与前沿组合解的唯一性无关,这说明该任意项对组合前沿未做任何贡献.不过需要指出的是,根据蒋春福和戴永隆[13],该任意项对证券组合有效子集的研究是有启发意义的,也就是说,可以通过该任意项的不同取值来调整证券的投资比例,使得某些证券的投资比例为零,那么这些证券自然就成了冗余证券。 [1] Fan J, Zhang J, Yu K. Vast portfolio selection with gross-exposure constraints[J]. Journal of the American Statistical Association, 2012, 107(498): 592- 606. [2] Buser S A. Mean-variance portfolio selection with either a singular or nonsingular variance-covariance matrix[J]. Journal of Financial and Quantitative Analysis, 1977, 12(3): 347-361. [3] Ryan P J, Lefoll J. A comment on mean-variance portfolio selection with either a singular or nonsingular variance-covariance matrix[J]. Journal of Financial and Quantitative Analysis, 1981, 16(3): 389-395. [4] Szegö G P. Portfolio theory: with application to bank asset management[M]. New York: Academic Press, 1980. [5] VöRöS J. The explicit derivation of the efficient portfolio frontier in the case of degeneracy and general singularity[J]. European Journal of Operational Research, 1987, 32(2): 302-310. [6] Korki B, Turtle H J. A note on the analytics and geometry of limiting mean-variance investment opportunity sets[J]. Review of Quantitative Finance and Accounting, 1997, 9(3): 289-300. [7] 史树中,杨杰.证券组合选择的有效子集[J].应用数学学报,2002,25(1):176-186. [8] 姚海祥,易建新,李仲飞.奇异方差-协方差矩阵的n种风险资产有效边界的特征[J].数量经济技术经济研究,2005,22(1):107-113. [9] 苏咪咪,叶中行.协方差矩阵奇异情况下的最优投资组合[J].应用概率统计,2005,21(3):244-248. [10] 蒋春福,戴永隆.奇异协方差阵下有效前沿及有效组合的解析解[J].系统科学与数学,2008,28(9):1134-1147. [11] Zhang S M, Wang S Y, Deng X T. Portfolio selection theory with different interest rates for borrowing and lending[J]. Journal of Global Optimization, 2004, 28(1): 67-95. [12] Dunne T T, Stone M. Downdating the moore-penrose generalized inverse for cross-validation of centred least squares prediction[J]. Journal of the Royal Statistical Society: SeriesB, 1993, 55(2): 369-375. [13] 蒋春福,戴永隆.奇异协方差阵下证券组合的有效子集[J].应用概率统计,2008,24(5):484- 492. Analytic Solutions of Mean-Variance Model with Singular Covariance Matrix and Different Interest Rates for Borrowing and Lending JIANG Chun-fu1, PENG Hong-yi2 (1.CollegeofMathematicsandComputationalScience,ShenzhenUniversity,Shenzhen518060,China; 2.CollegeofScience,SouthChinaAgriculturalUniversity,Guangzhou510642,China) In the mean-variance portfolio model, the covariance matrix is likely to be singular since the multi-collinearity and correlation can arise from the increase of financial assets, especially when considering a large-scale portfolio. In view of this situation, we reconsider the mean-variance portfolio problem under singular covariance matrix. A new approach based on generalized inverse matrix is proposed as a remedy for the deficiency of conventional methods in which covariance matrix is constrained to be invertible. The analytic solutions of frontier portfolio and portfolio frontier are derived with different interest rates for borrowing and lending, which extending successfully the classic Markowitz portfolio model. financial engineering; portfolio; moore-penrose generalized inverse; different interest rates for borrowing and lending 2011- 05-21 国家自然科学基金资助项目(71101095);广东省自然科学基金资助项目(2008276) 蒋春福(1977-),男,湖南永州人,博士,副教授,研究方向:投资组合,金融风险管理。 F224;O212 A 1007-3221(2015)02- 0192- 09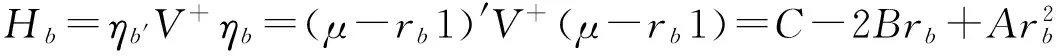
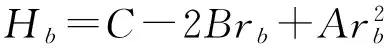
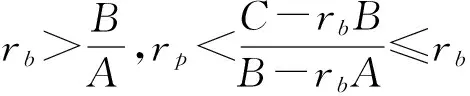
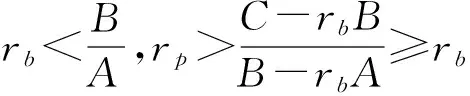
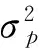

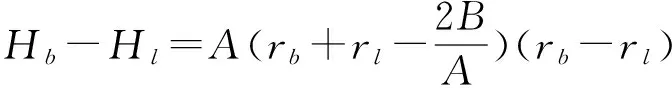
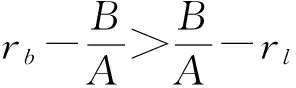

2 数值算例


3 结语
