数学诊所
2015-07-06张绿波
新课程·小学 2015年5期
张绿波
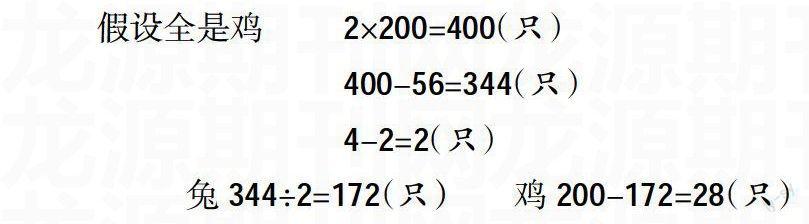

在解答鸡、兔同笼问题时,不少学生没有掌握鸡、兔同笼问题的基本格式,盲目生搬硬套,导致出错。
病例:鸡、兔共200只,兔脚比鸡脚多56只,求鸡、兔各有多少只?
假设全是鸡 2×200=400(只)
400-56=344(只)
4-2=2(只)
兔344÷2=172(只) 鸡200-172=28(只)
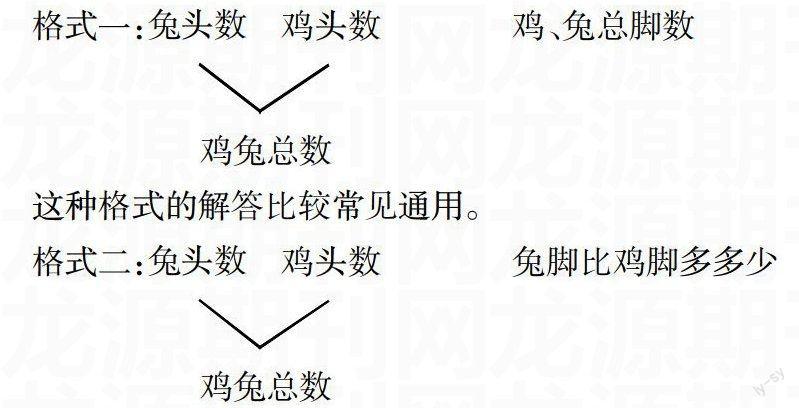
诊断:本案例没有分清鸡、兔同笼问题的基本格式,盲目生搬硬套,导致出错。鸡、兔同笼问题有两种基本格式,解答方法也略有差异。
这种格式的解答比较常见通用。
这种格式的解答可以例表假设发现规律:
由此发现,当假设全是兔、鸡,鸡脚就比兔脚多出800只,然后,多将一只兔调换成鸡以后,兔脚比鸡脚多的只数就会少6只,这样离题目中所说的兔脚比鸡脚多56只说接近了6只,这样也容易算出需要将12只兔子调换成鸡。
处方:假设全是兔
4×200=800(只)
800-56=744(只)
4+2=6(只)
鸡头数 744÷6=124(只)
兔头数 200-124=76(只)
注意事项:解答鸡、兔同笼问题一定分清要的格式是哪一种,然后假设例举,找到规律,切不可盲目生搬,要分清鸡脚和兔脚是该相加还是相减,从而使问题得到解决。
编辑 孙玲娟
