基于P-T模型估算雨养大豆田蒸散量

吴文心 贾志军 董一平

1)(江西省上饶市气象台，上饶 334000)2)(成都信息工程学院大气科学学院/高原大气与环境四川省重点实验室，成都 610225)



基于P-T模型估算雨养大豆田蒸散量

吴文心1)贾志军2)*董一平2)

1)(江西省上饶市气象台，上饶 334000)2)(成都信息工程学院大气科学学院/高原大气与环境四川省重点实验室，成都 610225)

基于2005—2007年涡度相关系统实测值和小气候观测资料，利用Priestley-Taylor(简称P-T)模型对三江平原雨养大豆田5—10月的蒸散量进行模拟和分析。结果表明：P-T模型参数α采用常规值1.26时，大豆出苗前和生长期模拟值明显大于实测值，大豆收割后模拟值明显小于实测值，模型不能用于模拟大豆田蒸散量。大豆生长期内参数α与叶面积指数呈对数正相关关系；当饱和水汽压差较小时，参数α与其呈幂函数正相关关系，当饱和水汽压差较大时，参数α与其呈幂函数负相关关系。大豆出苗前参数α与太阳辐射呈正相关关系，与饱和水汽压差呈负相关关系；大豆收割后参数α与风速呈显著正相关关系。依据回归方程修正参数α后，多个用于检验模型模拟效果的统计量均表明：P-T模型对不同时期大豆田蒸散量的模拟精度明显提高，能够较好地估算大豆田蒸散量。总而言之，P-T模型必须修正参数α方可用于估算三江平原雨养大豆田蒸散量。

P-T模型； 参数α； 蒸散量； 雨养大豆田

引 言

农田生态系统在全球生态环境、能量平衡和区域气候研究中具有重要地位, 对农田地表蒸散量的研究一直是国际上关注的热点问题[1]，特别是提高农田蒸散量估算精度不仅对于研究全球气候变化和水资源评价具有重要作用，而且对于农作物需水生产管理、旱情监测预测、水资源有效开发利用等方面亦有十分重要的应用价值[2-6]。Priestley-Taylor(简称P-T)模型在诸多蒸散模型中具有较强的机理性，其忽略了湍流输送条件对水分蒸散的影响，所需气象变量较少，在区域水分蒸散模拟研究中得到了广泛应用。Nurit等[7]在双源地表能量平衡模型中基于P-T模型估算了农作物冠层蒸散量，刘绍民[8]在农田蒸散试验资料的基础上用P-T模型计算了新疆棉田实际蒸散量，吕厚荃等[9]基于P-T模型估算了华北地区玉米田实际蒸散量，米娜等[10]比较分析了Hargreaves，FAO Penman-Monteith模型和P-T模型对玉米农田蒸散量的模拟精度，研究表明，作物系数采用分段单值法时P-T模型模拟结果最优。基于P-T模型修正式，Sumner等[11]对美国佛罗里达州非灌溉牧草地、Pereira[12]对巴西湿热气候和美国半干旱气候条件下的野生植被以及Stannard[13]对美国圣路易斯山谷半干旱牧草地野生植被的蒸散量均获得了较好的模拟效果。然而P-T模型参数α的取值对蒸散量的估算精度具有决定性作用。在下垫面湿润条件下参数α取常数1.26能够取得较好的模拟效果[14]，但一些学者分析实际观测资料发现，参数α不是常数，具有日变化和季节变化特征[15-16]，同时许多研究也表明：受研究区地理条件、海陆间平流输送和年降水量变化等影响，参数α变异性显著[3，12-13，17-19]，与土壤湿度[5，8-9，17]、饱和水汽压差[7，20]、太阳辐射[11]、叶面积指数[5，8-9，11]、耦合系数[12]等因子密切相关。因此，应用P-T模型估算蒸散量时，要依据研究区下垫面和气候特征等因素确定参数α合适的数值。

三江平原是我国重要的商品粮生产基地，大豆田为典型雨养旱作农田。近年来，在全球气候异常背景下，该区域生长季内和年际间降水量差异比较显著，降水量直接控制着土壤含水量和大豆田蒸散量，进而影响大豆生长发育和产量。研究表明：土壤水分含量充足时，蒸散量主要受大气蒸发需求的影响，P-T模型参数α随大气蒸发需求的增加而增加[14]，一旦土壤含水量下降，参数α会因水分蒸散表层阻力的明显增加而减小[17]。就三江平原气候特征而言，P-T模型对大豆田蒸散量的模拟效果如何、参数α是否需要修正以及修正后模拟效果如何，这些问题目前尚不明确，有待深入探究与评价。本研究以涡度相关系统测量值为标准，通过分析P-T模型对三江平原大豆田蒸散量的模拟效果，明确估算P-T模式对于大豆田蒸散量的适用性，为评价该地区大豆田水分状况、提高水资源利用率以及预测大豆产量提供依据。

1 资料和方法

1.1 资料来源

1.1.1 研究区概况

中国科学院三江平原沼泽湿地生态试验站(47°35′ N，133°31′E)位于东北三江平原腹地黑龙江省同江市辖区，属温带湿润大陆性季风气候，夏季温暖湿润，冬季严寒漫长，冻结期长达7～8月。年平均气温为1.9℃，1月平均气温为-21℃，7月平均气温为22℃，年平均降水量约为600 mm，60%以上降水集中于6—8月。本研究试验点位于旱地试验场内的大豆田，地表水分主要来源于大气降水，在大豆生长期间没有任何灌溉措施，属典型雨养农田。大豆田土壤类型为潜育白浆土，地下水埋深6～7 m。由于白浆土具有难以透水的紧实黏土层，因此，降水量较大时地表有短期积水。观测期间大豆种植品种为绥化14-3，行距为0.65 m，南北陇向。5月初开始观测，5月中、下旬播种，播种前一次性施入肥料(N,P2O5和K2O施肥量分别为40 kg·hm-1,90 kg·hm-1和15 kg·hm-1)，5月下旬6月上旬出苗，9月中、下旬至10月初成熟收割，10月下旬结束观测。观测期间大豆发育期状况如表1所示。

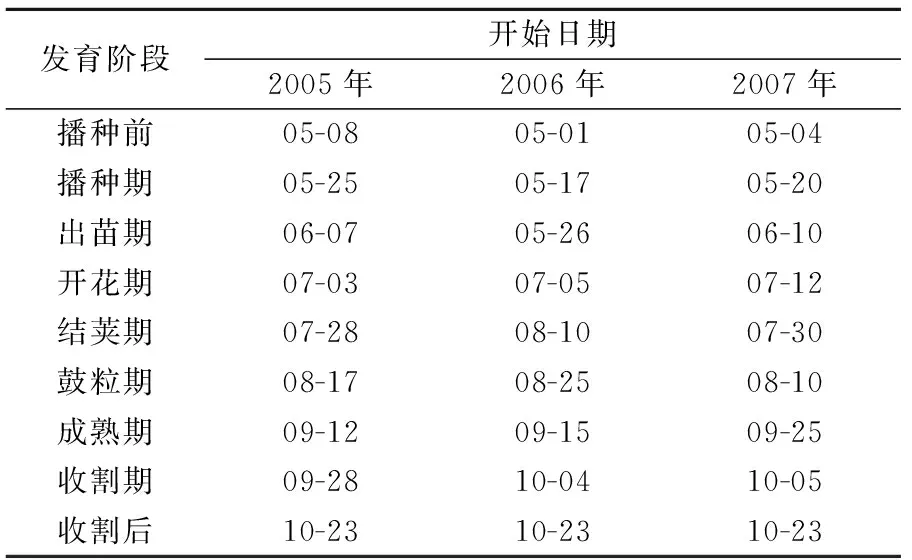
表1 大豆发育期状况Table 1 Developmental stages of soybean

注：播种前日期为涡度相关系统观测开始日期，收割后日期为涡度 相关系统观测结束日期。

1.1.2 数据来源和质量控制

2005—2007年5—10月利用布置在本研究试验点内的涡度相关系统对大豆田蒸散量进行连续观测。涡度相关系统主要由LI-7500开路式红外气体分析仪和CSAT3三维超声风速仪组成，分别用于测定CO2/H2O密度和三维风速，采样频率为10 Hz,实时数据和在线计算的30 min平均通量均存储于PC卡内。同时还利用小气候观测系统对主要环境因子进行观测，观测仪器主要包括CNR1净辐射传感器、HMP45C空气温湿度传感器和52203降水量传感器。此外，每隔10 d采用CI-203型叶面积仪测定大豆叶面积指数，用以反映植被发育的季节变化。

涡度相关技术作为测定地气间水热通量的标准方法在全球得到广泛应用，目前存在的主要问题是在涡度相关系统通量观测中能量不闭合现象较为普遍，国际通量网(FLUXNET)平均能量不闭合度约为20%[21]，能量平衡闭合程度已被作为评价涡度相关数据可靠性的方法，FLUXNET许多站点将能量平衡闭合状况分析作为一种标准程序用于通量数据的质量评价。该研究中由于缺乏必要的辅助观测数据，无法进行能量平衡闭合状况分析，但现有研究表明：作物生长季能量闭合状况好于非生长季[21-23]，且植株低矮的农作物能量闭合程度明显较好[23-24]。该研究主要观测了大豆发育期间地表蒸散量，且大豆发育期间最大高度约为75 cm，赵晓松[25]对该研究中的涡度相关数据进行了大气湍流统计特征分析、谱分析、通量贡献区评价、倾斜校正和超声湿度校正，结果表明：总体而言，该观测所获得的通量数据可信度较高，能够代表观测区域通量大小。该研究中，大豆田观测点下垫面平坦均质，有足够的通量贡献区，因此，主要考虑夜间通量低估带来的系统误差。目前多数研究者利用夜间湍流通量与表征湍流强度大小的摩擦风速(u*)的关系剔除夜间弱湍流交换下的通量值[26]，该研究中剔除标准为u*< 0.1 m·s-1，被剔除的数据按缺测数据处理。此外，在涡度相关系统实际观测中，由于传感器故障、降水、感应器维护和断电等原因，不可避免地会出现缺测。2005—2007年观测期间数据缺测率(包括被剔除的异常数据)分别为16.7%，31.9%和21.4%，明显低于FLUXNET 35%的平均值[27]。缺测通量数据依据下述方法进行插值：小于2 h的数据空缺，采用线性外推法插补；不小于2 h的数据空缺，采用查表法插补，查表法是生态系统能量通量标准插补方案的首选方案[28]。

1.2 模型与方法

1.2.1 P-T模型

Priestley和Taylor以平衡蒸发为基础，通过引进参数α, 导出最小平流条件下蒸发力的估算公式[4]，即

(1)

式(1)中，E0为参考作物蒸散量(单位：mm·d-1)，Δ为饱和水汽压曲线斜率(单位：kPa·℃-1)，γ为干湿球湿度方程常数(取值0.066 kPa·℃-1)，Rn为日总净辐射，G为土壤热通量，Rn和G单位需换算为mm·d-1,α为量纲为1的经验系数，当取值为1.26时，该公式估算值为湿润条件下的参考作物蒸散量。依据参考作物蒸散量估算实际蒸散量需考虑植被发育和地表水分供给条件的影响。为了简化计算过程，本研究利用P-T修正式估算实际蒸散量Ea，其表达形式为

(2)

式(2)主要考虑了非理想条件下的蒸散量，参数α是一个关于环境因子x1，x2，…,xi的经验函数，要依据研究区域的实际环境条件确定[11]。日尺度上计算蒸散量时土壤热通量G与净辐射Rn相比很小，通常可以忽略[29]。

1.2.2 方 法

本研究以涡度相关系统测量值为标准，通过分析修正参数α前后P-T模型对大豆田蒸散量的模拟效果，明确该模型在三江平原大豆田的适用性。首先评估参数α取常规值1.26时P-T模型对2006年大豆田的模拟效果，然后依据2005年和2007年实测值反推出参数 ，利用SPSS19.0软件分析其与环境因子的关系，以2006年实测值对P-T修正式进行验证。本研究中评价模型模拟效果的方法除了对实测值与模拟值进行线性回归分析外，还引入平均偏差、均方根误差和模拟效率，多角度统计分析模拟值的准确性[30]。

2 结果与分析

2.1 P-T模型参数α常规值模拟结果

图1为P-T模型参数α取常规值1.26时，依据小气候观测资料和式(1)估算大豆田蒸散量，并与涡度相关系统实测值进行比较得出的不同时期模拟结果。由图1a可见，大豆出苗前模拟值明显大于实测值，且散点分布相当分散，平均偏差为1.65 mm·d-1，均方根误差为2.10 mm·d-1。由图1b可见，大豆生长期内(从出苗至成熟期)散点绝大多数位于1:1线上侧，偏差明显减小，平均偏差和均方根误差分别为1.22 mm·d-1和1.49 mm·d-1。由图1c可见，大豆收割后模拟值明显小于实测值，散点分布也较分散，平均偏差和均方根误差分别为-0.74 mm·d-1和0.86 mm·d-1。图1给出了蒸散量实测值与模拟值之间的线性回归方程，显然在大豆生长期和收割后回归方程可靠性较高，其决定系数R2较大，且达到0.01显著性水平(p<0.01)，说明模拟值变化特征与实测值一致，但不同时期的模拟效率均为负值(大豆出苗前、生长期和收割后模拟效率分别为-3.00，-0.90，-1.43)，表明模拟值与实测值差距较大，P-T模型不能用于估算大豆田蒸散量。

由图1可见，P-T模型估算值有大有小，在大豆出苗前明显高于实测值，在大豆收割后又明显低于实测值，在大豆生长期间系统偏大。偏差的这种变化可能与参数α取常数有关。依据2006年实测资料反推出参数α的季节变化趋势如图2所示。大豆出苗前和生长期参数α平均值分别为0.76(±0.42)和0.86(±0.27)，而在大豆收割后参数α明显增大，平均值为2.20(±0.74)。Priestley等[14]推荐的参数α(平均值为1.26)适用于湿润下垫面，而三江平原大豆田水分主要来源于大气降水，降水量的季节和年际变化使地表水分条件变化很大，从而使参数α变异性较大，具有很强的经验性，因此，P-T模型参数α采用常规值1.26必然会产生较大误差，有必要依据三江平原大豆田实际条件修正参数α。

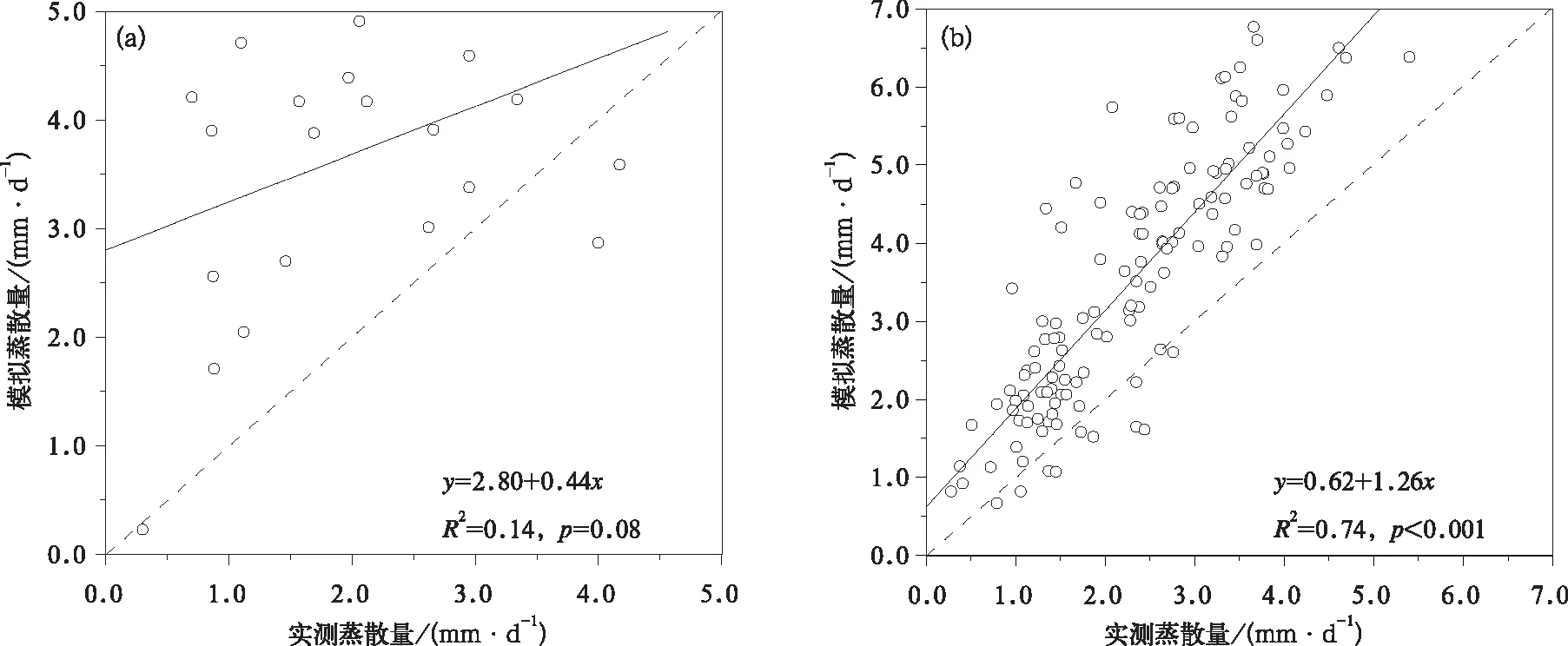
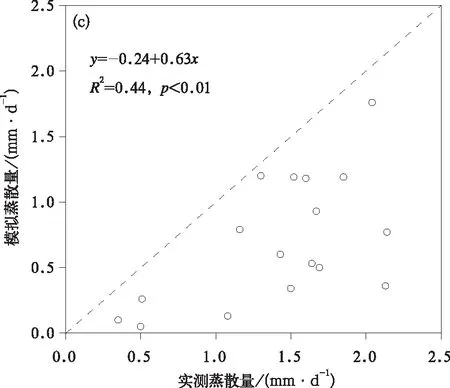
图1 基于P-T模型参数α常规值的大豆田不同阶段蒸散量模拟值与实测值比较 (a)出苗前，(b)生长期，(c)收割后 Fig.1 Comparison of observed evapotranspirations and those simulated by P-T model based on conventional values of α during different period (a)before emergence，(b)growing season，(c)after harvest

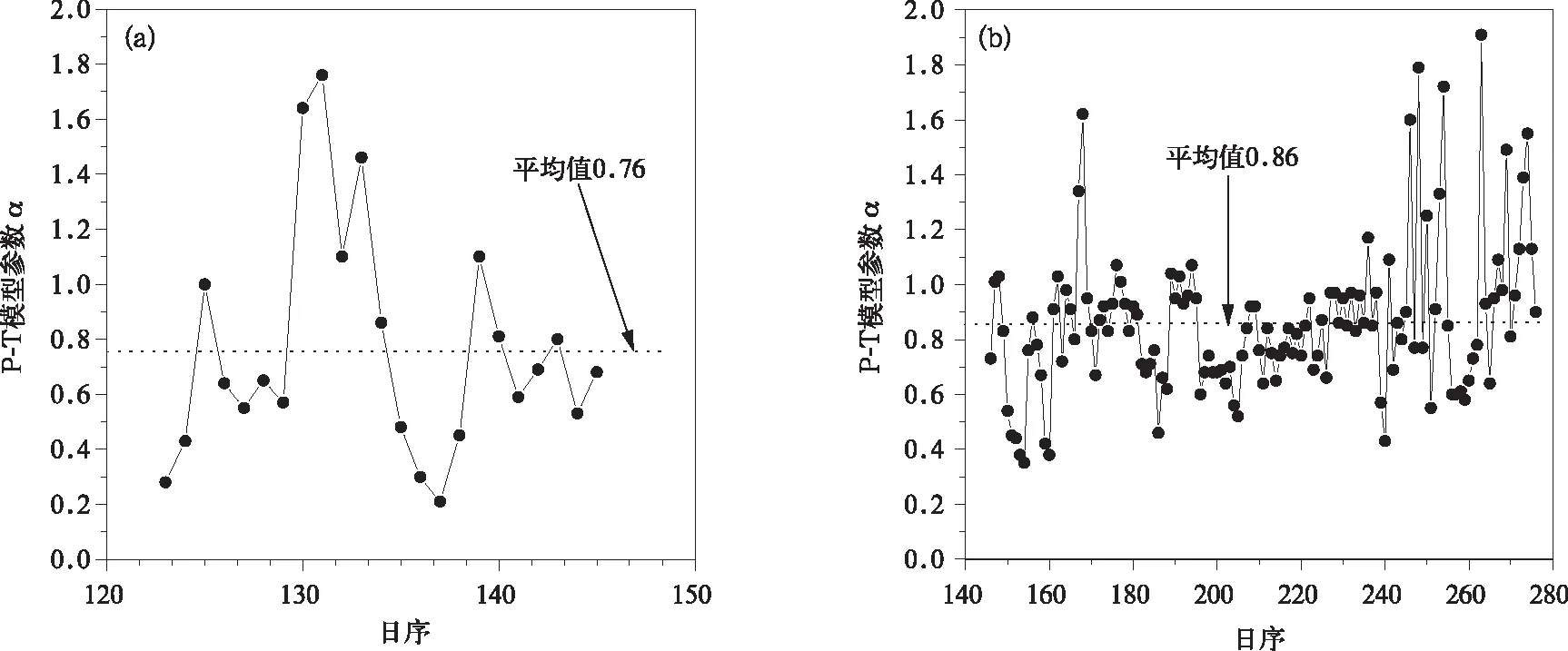
图2 不同时期大豆田P-T模型参数α变化特征(a)出苗前，(b)生长期，(c)收割后Fig.2 Variation characteristics parameter α of P-T model over soybean field during different period(a)before emergence，(b)growing season，(c)after harvest

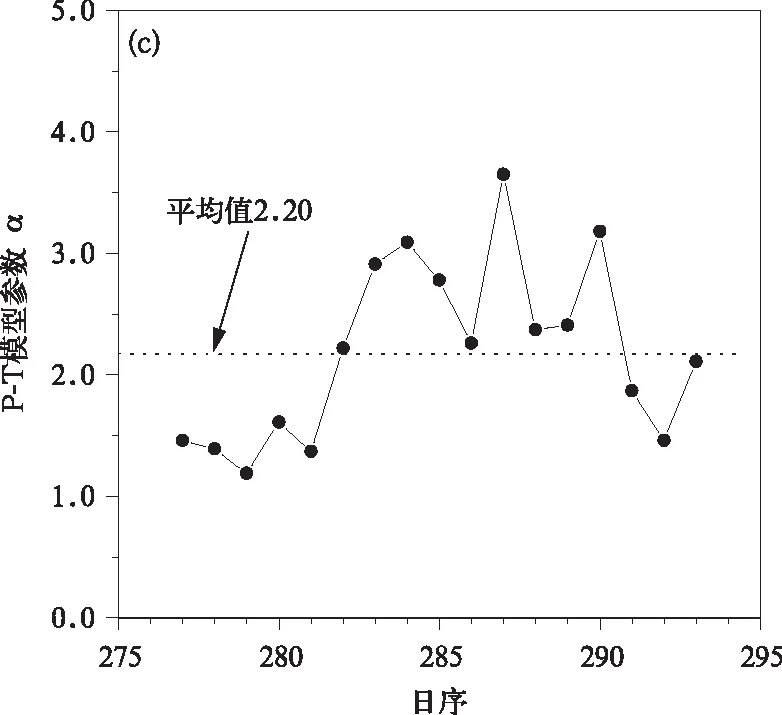
续图2

2.2 P-T模型参数α修正

利用2005年和2007年5—10月涡度相关系统蒸散量实测值和同期观测的小气候资料，依据式(2)反推计算得到各日参数α，分析其与生物和气候因子的相关性。作物生长期内蒸腾作用是水分蒸散的重要组成部分，在植被生长旺盛期尤为明显[31]，因此大豆叶面积指数是农田蒸散量的一个重要影响因子。如图3所示，参数α随叶面积指数的增加呈增加趋势，二者呈对数显著正相关关系，表明叶面积指数是影响参数α的一个重要因子。这与Burba等[5]对美国俄克拉荷马州冬小麦、刘绍明[8]对中国新疆棉田P-

T模型α参数的研究结论一致。饱和水汽压差是水汽从蒸发面输送到周围大气的直接驱动力，但饱和水汽压差对参数α的影响方式与饱和水汽压差变化范围有关。如图3b所示，参数α随饱和水汽压差的增加表现出先增加、后降低的变化趋势。利用二者建立的一元二次回归方程得出转折点为饱和水汽压差D=5.05 hPa，当D< 5.05 hPa时，参数α与D呈正相关关系；当D> 5.05 hPa时，参数α与D呈负相关关系。

进一步分析饱和水汽压差D不同变化范围内二者的关系，结果如图4所示。当D<5.05 hPa时，参数α与D呈幂函数正相关关系(幂函数的指数为正值)；当D>5.05 hPa时，参数α与D呈幂函数负相关关系(幂函数指数为负值)。通常情况下，饱和水汽压差D增加能够促进水分输送，使蒸散量增加，因此，在其他条件相同的情况下，特别是地表水分供给充足的条件下，参数α与D呈正相关关系[7]。但地表水分条件是控制蒸散的首要因子，三江平原大豆田属于雨养农田，农田土壤水分仅来源于自然降水，久旱少雨使土壤含水量下降，地表蒸发和作物蒸腾作用逐渐减弱，导致近地层水汽含量下降而气温升高，干旱条件下蒸散量与近地表温度呈负相关关系[32]，进而表现为参数α与D呈负相关关系[20]。由此可见，久旱少雨时饱和水汽压差D的大小在一定程度上反映了地表的干旱程度。

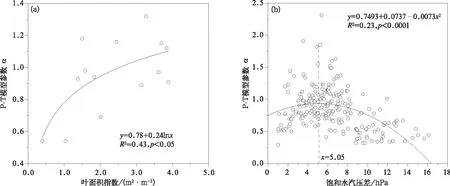
图3 大豆生长期内叶面积指数(a)和饱和水汽压差(b)对P-T模型参数α的影响Fig.3 Effects of LAI(a) and D(b) on parameter α of P-T model during growing season of soybean

为确定P-T模型修正式的表达式，以参数α为因变量，以叶面积指数L与饱和水汽压差D为自变量，依据图3和图4所揭示的函数关系，确定函数α的非线性回归方程表达式为α=alnL+bDc。a,b和c为方程参数，大小反映了叶面积指数L与饱和水汽压差D对参数α影响程度，其值越大，表明影响程度越大，且参数c的正负决定了参数α与D是正相关还是负相关。利用SPSS19.0统计软件进行迭代计算，以确定各参数值大小。结果如表2所示，非线性回归方程中参数α与叶面积指数L与饱和水汽压差D的关系，与图3和图4所揭示的规律完全一致，但回归方程参数a和b的标准差均较大，说明此估算值的显著性水平不显著。相比之下，参数c的标准差均较小，说明此估算值的显著性水平较显著。非线性回归方程的决定系数R2较高，叶面积指数L与饱和水汽压差D能够解释参数α变化的78.6%和67.9%，表明方程的拟合度较高。

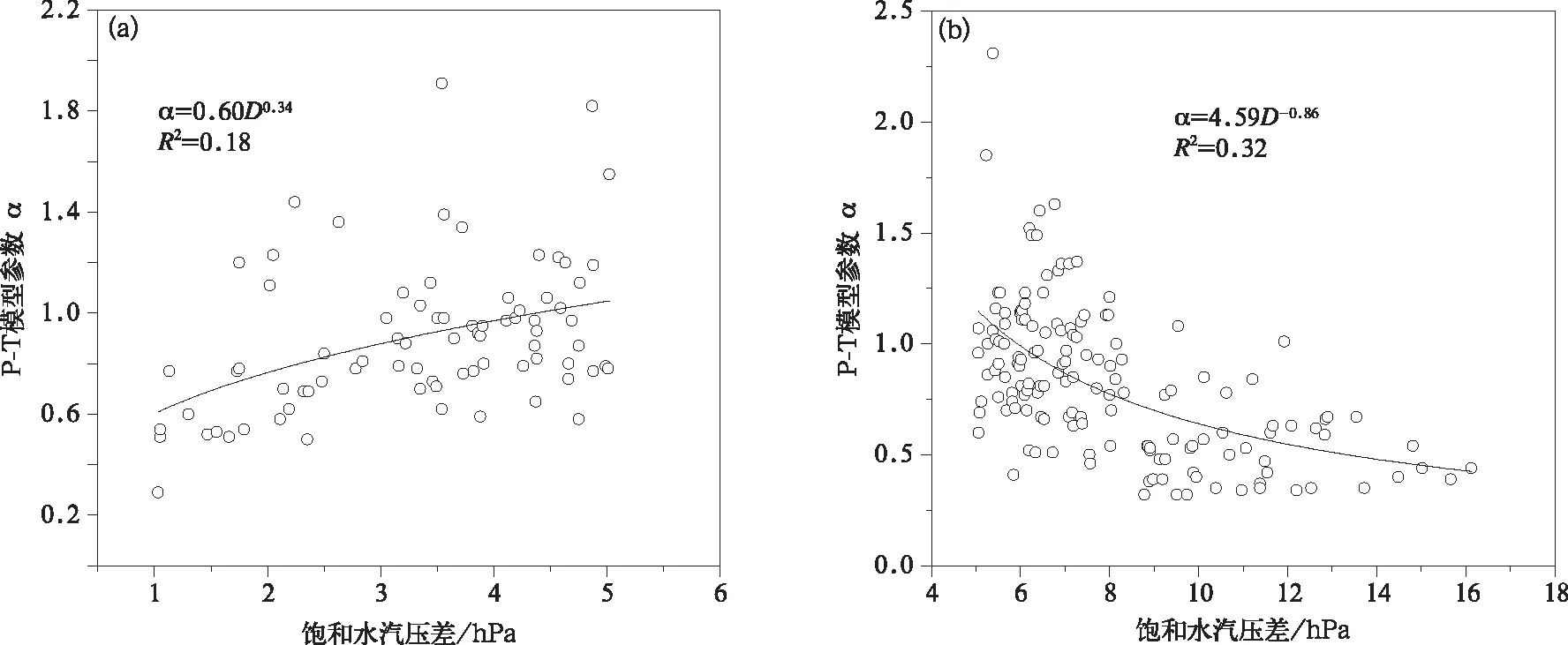
图4 不同饱和水汽压差(D)对P-T模型参数α的影响 (a)D<5.05 hPa，(b)D>5.05 hPaFig.4 Effects of D on parameter α of P-T model under different conditions(a)D<5.05 hPa，(b)D>5.05 hPa

条件参数a(±标准差)参数b(±标准差)参数c(±标准差)R2样本量D<5.05hPa0.083(±0.087)0.195(±0.105)1.294(±0.376)0.78680D>5.05hPa0.108(±0.128)5.246(±6.102)-0.953(±0.596)0.679150

大豆出苗前和收割后，气象因子是控制水分蒸散的主要因子，为进一步定量描述参数α与环境因子的关系，在剔除模型中已包含的变量后，以参数α和环境因子分别为因变量和自变量，利用SPSS19.0软件采用多元逐步回归方法建立多元一次统计模型，入选模型的影响因子、回归系数和显著性检验结果如表3所示。大豆出苗前，参数α主要受太阳辐射Ra与饱和水汽压差D控制，参数α与Ra呈正相关关系，而与D呈负相关关系。饱和水汽压差D标准回归系数的绝对值明显大于太阳辐射Ra的标准回归系数，说明D对参数α的影响作用要强于Ra的影响。参数α与Ra和D建立的回归方程能够解释参数α变化的39.1%。

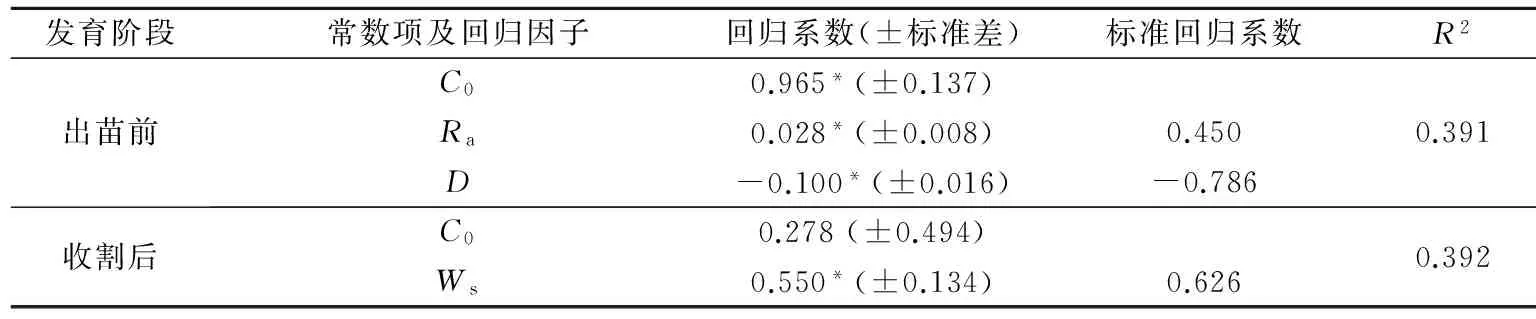
表3 大豆出苗前和收割后P-T模型参数α的统计模型Table 3 Statistical models of parameter α of P-T model before soybean emergence and after soybean harvest

注：*表示达到0.001显著性水平。

大豆收割后参数α主要受风速Ws控制，Ws能够解释参数α变化的39.2%。D和Ws是维持地表水分蒸散的必要条件，二者增加均能够促进水分蒸散，因此与P-T模式参数α呈正相关关系。三江平原地区属春旱多发区，大豆出苗前D因子回归系数为负值，反映了干旱对水分蒸散的抑制作用。太阳辐射是地表能量的直接来源，因此,参数α与Ra呈正相关关系，Sumner等[11]针对牧草地蒸散量建立的参数α经验函数也证明了这个结论。

2.3 P-T模型修正式验证

依据修正后的α函数代入式(2)对P-T模型修正式进行验证，结果如图5所示。由图5a可见，大豆出苗前P-T修正式模拟精度明显提高，散点较均匀地分布于1:1线两侧，平均偏差和均方根误差分别为0.06 mm· d-1和0.60 mm· d-1，较参数修正前分别下降了96.4%和71.4%，明显接近于理想值(0 mm·d-1)；模拟效率由负值转变为正值(0.57)，接近于理想值1，表明模型模拟精度较高。由图5b可见，大豆生长期内P-T修正式模拟精度也明显提高，散点较均匀地分布于1:1线两侧，尽管散点离散程度相对偏大，但平均偏差和均方根误差较参数修正前分别下降87.7%和38.3%，达到0.15 mm·d-1和0.92 mm·d-1，模拟效率由负值转变为正值(0.28)，表明模型能够用于估算大豆田生长期蒸散量。由图5c可见，大豆收割后P-T修正式模拟精度也明显提高，尽管大部分散点分布于1:1线下侧，但散点离散程度明显减小，平均偏差和均方根误差分别为-0.21 mm·d-1和0.41 mm·d-1，较参数修正前分别下降了71.6%和52.3%；模拟效率由负值转变为正值(0.42)，表明模型能够用于估算大豆收割后的地表蒸散量。蒸散量实测值与模拟值之间线性回归方程的截距、斜率和决定系数R2如图5中公式所示，其数值大小较参数α修正前明显接近于其理想值(分别为0，1和1)，这也表明，P-T修正式估算精度明显提高。P-T模型参数α是关于环境因子的经验函数，因此，依据研究区域环境条件确定参数α亦能提高模型估算精度[33]，其他学者修正P-T模型参数α后也得到了相同的结论。Sumner[11]拟合建立了关于太阳辐射和叶面积指数的参数α函数后，很好地估算了牧草地半小时蒸散量；Pereira[12]研究了湿热气候和半干旱气候条件下P-T模型的模拟精度，结果表明:P-T模型参数α与耦合系数呈倒数关系，据此修正参数α后P-T模型的模拟值与蒸渗仪测量值具有很好的一致性。Stannard[13]利用叶面积指数和土壤蒸发量修正参数α后，P-T模型很好地模拟了半干旱牧草地野生植被的蒸散量。刘绍民[8]和吕厚荃等[9]分别基于P-T模型，结合作物叶面积指数和土壤湿度,建立了适用于干旱地区棉田和华北地区玉米田的实际蒸散量计算模式。

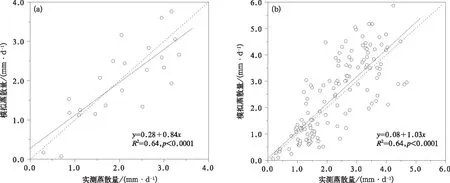
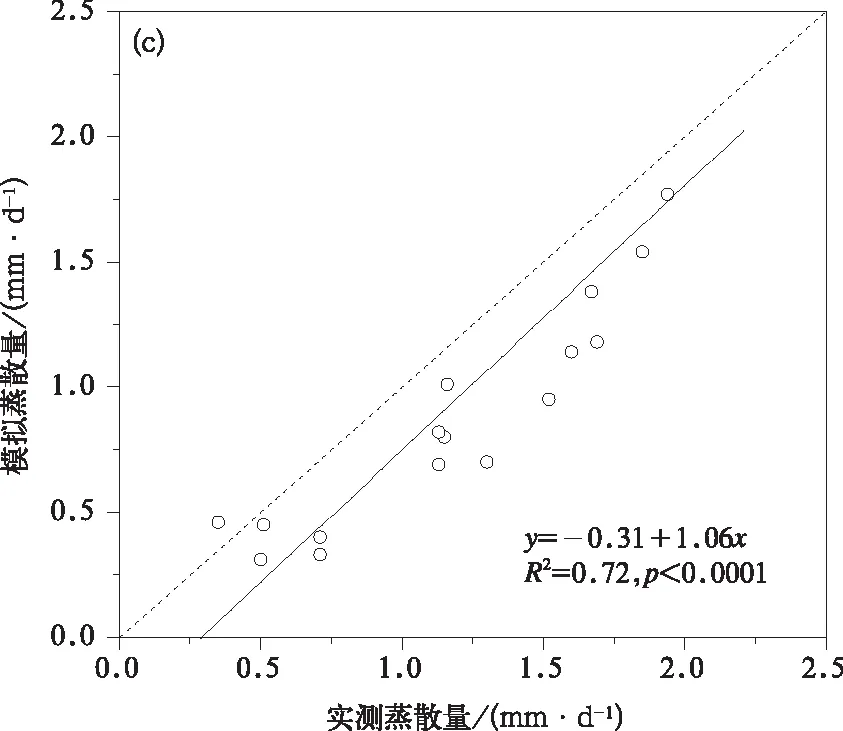
图5 基于P-T模型参数α修正值的大豆田不同阶段蒸散量模拟值与实测值比较 (a)出苗前，(b)生长期，(c)收割后 Fig.5 Comparison of observed evapotranspirations and those simulated by P-T model based on modified α value during different periods (a)before emergence，(b)growing season，(c)after harvest

整体而言，参数α修正后，P-T模型对模拟精度均明显提高，能够用于估算雨养大豆田不同阶段的蒸散量。但在大豆收割后模拟值明显小于实测值，这可能与大豆收割后农田翻耕、气温显著下降有关。另外，本研究在分析P-T修正式对大豆田蒸散量模拟效果时，仅用1年数据进行验证，其结果缺乏普遍性，今后将利用三江平原其他区域、其他年份的大豆田蒸散量实测资料进一步评估其模拟效果。

3 结 论

本文以2005—2007年实测蒸散量和气象因子资料，分析了P-T模型对雨养大豆田蒸散量的模拟效果，主要结论如下：

1) P-T模型参数α采用常规值1.26模拟效果较差，在大豆出苗前和生长期模拟值明显大于实测值，而在大豆收割后模拟值明显小于实测值，不能用于估算大豆田蒸散量。

2) P-T模型参数α与环境因子密切相关。大豆生长期内参数α与叶面积指数呈对数正相关关系；当饱和水汽压差D较大时参数α与D呈幂函数负相关关系，而当饱和水汽压差D较小时参数α与D呈幂函数正相关关系；大豆出苗前参数α与太阳辐射呈正相关关系，与D呈负相关关系；大豆收割后α与风速呈显著正相关关系。

3) 依据回归分析结果修正参数α后，P-T模型模拟精度明显提高，对不同时期大豆田蒸散量均取得了较好的模拟效果，表明参数α修正后P-T模型才可用于估算三江平原雨养大豆田蒸散量。

[1] Lee T S，Najim M M，Aminul M H.Estimating evapotranspiration of irrigated rice at the west coast of the Peninsular of Malaysia.JournalofAppliedIrrigationScience，2004，39(1):103-117.

[2] 张顺谦,马振峰,张玉芳.四川省潜在蒸散量估算模型.应用气象学报,2009,20(6):729-736.

[3] Zhang Y Q，Liu C M，Yu Q，et al.Energy fluxes and the Priestley-Taylor parameter over winter wheat and maize in the North China Plain.HydrologicalProcesses，2004,18(12):2235-2246.

[4] 龚员石,李子忠,李春友.利用时域反射仪测定的土壤水分估算农田蒸散量.应用气象学报,1998，9(1):72-78.

[5] Burba G G，Verma S B.Seasonal and interannual variability in evapotranspiration of native tallgrass prairie and cultivated wheat ecosystems.AgriculturalandForestMeteorology，2005，135(1-4):190-201.

[6] 毛飞,张光智,徐祥德.参考作物蒸散量的多种计算方法及其结果的比较.应用气象学报,2000,11(增刊Ⅰ):128-136.

[7] Nurit A，William P K，Martha C.Application of the Priestley-Taylor approach in a two-source surface energy balance model.JournalofHydrometeorology，2010,11(1):185-198.

[8] 刘绍民.用Priestley-Taylor模式计算棉田实际蒸散量的研究.应用气象学报，1998,9(1):88-93.

[9] 吕厚荃,钱拴,杨霏云,等.华北地区玉米田实际蒸散量的计算.应用气象学报，2003,14(6):722-728.

[10] 米娜,陈鹏狮,张玉书,等.几种蒸散模型在玉米农田蒸散量计算中的应用比较.资源科学，2009，31(9):1599-1606.

[11] Sumner D M，Jacobs J M.Utility of Penman-Monteith，Priestley-Taylor，reference evapotranspiration and pan evaporation methods to estimate pasture evapotranspiration.JHydrol，2005，308(1-4):81-104.

[12] Pereira A R.The Priestley-Taylor parameter and the decoupling factor for estimating reference evapotranspiration.AgriculturalandForestMeteorology，2004,125(3-4):305-313.

[13] Stannard D I.Comparison of Penman-Monteith，Shuttleworth-Wallace and modified Priestley-Taylor evapotranspiration models for wildland vegetation in semiarid rangeland.WaterResourcesResearch，1993，29(5):1379-1392.

[14] Priestley C H B，Taylor R J.On the assessment of surface heat flux and evaporation using large-scale parameters.MonWeaRev，1972，100:81-92.

[15] Debrin H A R，Keijman J Q.The Priestley-Taylor evaporation model applied to a large shallow lake in the Netherlands.JAppliedMeteor，1979，18(7):898-903.

[16] Mukammal E I ,Neumann H H.Application of the Priestley-Taylor evaporation model to assess the influence of soil moisture on the evaporation from a large weighing lysimeter and class A Pan.Boundary-layerMeteorology，1977，12:243-256.

[17] Flint A L，Childs S W.Use of the Priestley-Taylor evaporation equation for soil water limited conditions in a small forest clear-cut .AgriculturalandForestMeteorology，1991，56(3-4):247-260.

[18] 马耀明.非均匀陆面上区域蒸发(散)研究概况.高原气象,1997,16(4):446-452.

[19] Xu C Y，Singh V P.Evaluation of three complementary relationship evapotranspiration models by water balance approach to estimate actual regional evapotranspiration in different climate regions.JHydrol，2005，308(1/4):105-121.

[20] Shi T T，Guan D X，Wang A Z，et al.Comparison of three models to estimate evapotranspiration for a temperate mixed forest.HydrologicalProcesses，2008，22:3431-3443.

[21] Wilson K B，Goldstein A H，Falge E，et a1.Energy balance closure at FLUXNET sites.AgriculturalandForestMeteorology，2002，113(1-4):223-243.

[22] 李正泉,于贵瑞,温学发,等.中国能量观测网络(ChinaFLUX)能量平衡闭合状况的评价.中国科学D辑:地球科学,2004,34(增刊Ⅱ):46-56.

[23] 刘渡,李俊,于强,等.涡度相关观测的能量闭合状况及其对农田蒸散测定的影响.生态学报,2012,32(17):5309-5317.

[24] 田红,伍琼,童应祥.安徽省寿县农田能量平衡评价.应用气象学报,2011,22(3):356-361.

[25] 赵晓松.三江平原沼泽湿地垦殖对CO2、水汽及能量通量的影响研究.北京:中国科学院研究生院,2008.

[26] Lafleur P M，Roulet N T，Admiral S W.Annual cycle of CO2exchange at a bog peatland.JournalofGeophysicalResearch:Atmospheres,2001,106(D3):3071-3081.

[27] Falge E，Baldocchi D D，Olson R J.Gap filling strategies for defensible annual sums of net ecosystem exchange.AgriculturalandForestMeteorology，2001,107(1):43-69.

[28] Falge E，Baldocchi D D，Olson R J.Gap filling strategies for long term energy flux data sets.AgriculturalandForestMeteorology，2001,107(1):71-77.

[29] 曾丽红,宋开山,张柏,等.应用Landsat数据和SEBAL模型反演区域蒸散发及其参数估算.遥感技术与应用,2008,23(3):255-263.

[30] Perez P J，Castellvi F，Martnez-Cob A.A simple model for estimating the Bowen ratio from climatic factors for determining latent and sensible heat flux.AgriculturalandForestMeteorology,2008,148:25-37.

[31] Kang S Z，Gu B J，Du T S，et al.Crop coefficient and ratio of transpiration to evapotranspiration of winter wheat and maize in a semi-humid region.AgriculturalWaterManagement,2003,59:239-254.

[32] 潘竟虎．黄土丘陵沟壑区蒸散的遥感反演:以静宁县水土保持世行贷款项目区为例．生态与农村环境学报,2008,24(4):6-9;41.

[33] Bormann H.Sensitivity analysis of 18 different potential evapotranspiration models to observed climatic change at German climate stations.ClimaticChange，2011,104(3-4):729-753.

Simulating Evapotranspiration of Rain-fed Soybean Field Based on P-T Model

Wu Wenxin1)Jia Zhijun2)Dong Yiping2)

1)(ShangraoMeteorologicalObservatoryofJiangxiProvince,Shangrao334000)2)(CollegeofAtmosphericSciences,ChengduUniversityofInformationTechnology,PlateauAtmosphereandEnvironmentKeyLaboratoryofSichuanProvince,Chengdu610225)

Based on eddy covariance measurements and microclimate observations available from 2005 to 2007, the simulating accuracy of evapotranspiration with P-T model of rain-fed soybean field from May to October in Sanjiang Plain is analyzed. Results indicate that simulated values of evapotranspiration by P-T model with conventional parameter (1.26) are significantly higher than observations before emergence and during the growing season of soybean, and the mean bias error (MBE) are 1.65 mm·d-1and 1.22 mm·d-1. However, simulated values are significantly lower than measurements after harvest, with the MBE of -0.74 mm·d-1. Modeling efficiency (ME) of P-T model are all negative values, which indicates that the model cannot be used in predicting evapotranspiration of soybean field during different periods. The cause may have much to do with the parameter, which is assumed as constant value of 1.26. According to measurements of evapotranspiration, the parameter is derived and shows obviously increasing trend during the whole observation periods. Average values of parameter before emergence, during the growing season, and after harvest are 0.76, 0.86 and 2.20, respectively. It is obvious that the parameter varies according to the growing phase, and it is necessary to modify the parameter based on the measured evapotranspiration of rain-fed soybean field in Sanjiang Plain.

Statistical analysis shows that leaf area index (LAI) is an important factor affecting evapotranspiration of soybean field. During the growing season, the parameter is creased with increasing LAI, following a logarithmic equation and a positive correlation. Vapor pressure deficit (VPD) is the direct driving force of transporting vapor from the surface to the surrounding atmosphere. The relationship between and VPD can be described empirically by a piecewise function: When the VPD is greater than 5.05 hPa, it’s a positive power function, but when the VPD is lower than 5.05, it’s a negative power function. The parameter is positively related to solar radiation and negatively related to VPD before soybean emergency and is positively related to wind speed after soybean harvest.

With parameter modified by using linear or non-linear regression equation, the estimation accuracy of P-T model under different periods are improved markedly. Before soybean emergency, MBE and root mean square error (RMSE) are 0.06 mm·d-1and 0.60 mm·d-1, reduced by 96.4% and 71.4%, respectively. ME is improved from a negative to a positive value (0.57) , close to the ideal value of 1. During the growing season, MBE and RMSE are 0.15 mm·d-1and 0.92 mm·d-1, reduced by 87.7% and 38.3%, respectively, and ME from a negative to a positive value (0.28). After soybean harvest, MBE and RMSE are -0.21 mm·d-1and 0.41 mm·d-1, reduced by 71.6% and 52.3%, respectively, ME turns from a negative into a positive value (0.42). It indicates that the modified P-T model can simulate the evapotranspiration of soybean field. In conclusion, P-T model is suitable to simulate the evapotranspiration only when the parameter is modified.

P-T model; parameterα; evapotranspiration; rain-fed soybean field

10.11898/1001-7313.20150210

高原大气与环境四川省重点实验室开放基金项目(PAEKL-2010-K3)，四川省教育厅应用基础研究项目(2009JY0117)

吴文心,贾志军,董一平. 基于P-T模型估算雨养大豆田蒸散量. 应用气象学报，2015，26(2)：221-230.

2014-08-13收到， 2015-01-09收到再改稿。

* 通信作者，email: jzj@cuit.edu.cn