一种Bayes降水概率预报的最优子集算法
2015-07-05胡邦辉刘善亮王学忠游大鸣张惠君
胡邦辉 刘善亮 席 岩 王学忠 游大鸣 张惠君
1)(解放军理工大学气象海洋学院,南京 211101)2)(中国人民解放军61741部队,北京 100081) 3)(南京军区气象水文中心,南京 210016)
一种Bayes降水概率预报的最优子集算法
胡邦辉1)*刘善亮2)席 岩3)王学忠1)游大鸣1)张惠君3)
1)(解放军理工大学气象海洋学院,南京 211101)2)(中国人民解放军61741部队,北京 100081)3)(南京军区气象水文中心,南京 210016)
MOS预报最优子集模型,通过消除数值模式系统性误差,可最大程度地提高其预报技巧。为了建立Naïve Bayes降水最优模型,利用2008—2011年T511数值预报产品和单站观测资料,对介休、运城、丰宁3个站Naïve Bayes降水概率分级预报模型进行研究。通过设计恰当的适应度函数,提出了一种用遗传算法搜寻Naïve Bayes模型最优子集的计算方案,得到了3个站的最优子集模型。结果表明:最优子集的拟合效果明显高于普通初始子集,能够显著提升数值模式在单站的预报技巧。最优子集模型主要通过降低数值模式空报率提高单站晴雨、小雨预报效果,通过小幅提高正确次数和降低空报次数改善对中雨预报效果。
遗传算法; 朴素贝叶斯分类器; 单站降水预报; 预报技巧
引 言
MOS原理下的不同预报模型,通过消除数值模式系统性误差,可以一定程度提高其预报技巧[1-5]。Naïve Bayes 分类器是一种近30年兴起的分类技术,其主要特点是概率化分类,与事件概率(全概率)不易考虑预报因子的影响不同,通过预报因子与条件概率之间的关系,可方便地计算出天气事件的后验概率,因而在欧美等气象技术先进国家得到广泛应用[6-7]。我国的气象工作者也相继开展Naïve Bayes 分类器的应用研究,2001年Liu等[8]利用1984—1992年香港地区的气象资料,采用Naïve Bayes分类、决策树分类和遗传算法相结合的方法,对降雨进行预报,取得了较好的效果。2007年王开宇等[9]利用北京地区4个站和南方地区3个站的30年的历史地面观测资料,分别建立两种Bayes分类器预报模型,并根据模型试报结果,分析了两种分类器不同地区准确性和稳定性差异。利用卫星资料和数值预报产品,郭雅芬等[10]将贝叶斯分类法有效地运用于预测青藏高原上中尺度对流系统的移动路径。苏君毅等[11]在朴素贝叶斯分类的基础上建立了一种增强型分类器系统,在中尺度对流系统预测的同时,对其移动方向与周边环境物理量场的分布特征进行分类研究,取得了较好效果。
最优子集回归(Optimal Subset Regression,OSR)[12]可以从预报因子所有可能的子集回归中以某种准则确定出一个最优回归方程,在天气预报和气候预测中应用广泛。谷德军等[13]利用多尺度最优子集回归方法预测南海夏季风爆发的日期,最大误差为8.5 d,取得了较好效果。柯宗建等[12]利用OSR方法对中国区域的季节降水进行降尺度预报,比较其与多模式集合预报的技巧,表明对中国区域冬夏降水预报均有改进。李玲萍等[14]利用欧洲中心格点资料,用最优子集回归建立0~72 h高温预报方程,2008年投入业务应用,预报效果较好。
Navïe Bayes分类器技术虽然先进,但其预报模型效果还与模型的预报因子有关,要求使用相关性高、物理意义明确的预报因子,但这类因子有多种,以降水预报为例,有模式输出降水量,各层的垂直速度、水汽、水汽通量、涡度平流等几十个,而预报模型因子数目以4~7个为宜,否则不能够充分反映降水信息或累积误差过大。如何从这几十个因子中选出4~7个因子,并使模型预报效果最好,成为建立Naïve Bayes预报模型面临的主要问题。但Naïve Bayes分类器显然不具备最优子集回归的算法体系,如果要逐一建模和比对,工作量过大。遗传算法(Genetic Algorithm, GA)的出现,使上述问题的解决成为可能。遗传算法借鉴生物界自然选择和基因遗传学原理,通过生物繁衍时基因的选择、交叉和变异与适应度的关系,刻画出生物群体、个体的进化过程,并形成了完整的理论和全局搜索算法体系[15]。本文尝试用遗传算法,搜寻Naïve Bayes模型的最优子集,以提高单站降水分级预报的效果。
1 资料及处理
1.1 资 料
数值预报产品:2008—2011年6—9月T511L60模式下发产品。产品包括温度、降水量等40个物理量,1000,925,850,700,500,400,300,250,200 hPa共9个层次。选用范围为15°~60°N,70°~140°E,水平分辨率为1°× 1°。起报时次为20:00(北京时,下同),预报间隔为6 h,预报时效为10 d。
单站降水量资料:介休、运城、丰宁3个站12 h降水量,时间同数值预报产品。
单站降水预报包括晴雨和降水量等级。其中,降水量等级根据12 h降水级别标准[16]划分,具体为小雨(0.1~4.9 mm)、中雨(5.0~14.9 mm)、大雨(15.0~29.9 mm)、暴雨(不低于30 mm)。
1.2 预报因子
利用T511数值预报产品,分别计算单层或多层格点上的沙氏指数、对流有效位能等诊断量[17-18],再根据物理意义及与预报对象的相关性,从相对湿度、比湿、地面温度、2 m温度、温度、温度露点差、水汽通量、水汽通量散度、地面气压、海平面气压、风向、垂直速度、涡度、散度、Q矢量涡度、Q矢量散度、螺旋度、位温、假相当位温、降水量、土壤湿度、总云量、24 h变温、条件性稳定度指数、湿理查森数、底层风速、对流有效位能、对流抑制能量和沙氏指数30个物理量中,选取22个预报因子。
1.3 消空处理
暴雨是小概率天气事件,在大部分样本中不会发生。为了提高预报效率,有必要在建模和预报前,依据暴雨发生条件,对样本集进行消空操作。消空条件为垂直速度小于0 m·s-1、比湿小于5 g·kg-1,消空处理的样本分两种情况:第1种针对建模样本,若不满足上述条件,则剔除该个例,否则保留;第2种针对试报样本,若不满足条件,则直接预报无暴雨发生,否则代入预报模型运算。
2 原理和算法
2.1 Naïve Bayes原理简介
降水分为4类,依次用类别变量(C1,C2,C3,C4)代表小雨、中雨、大雨、暴雨。这里以小雨为例,假定选出T511数值预报产品的相对湿度、比湿、地面温度、2 m温度、温度和降水量6个预报因子(x1,x2,…,x6)和水汽通量、水汽通量散度、地面气压、海平面气压、风向、垂直速度6个预报因子(y1,y2,…,y6)作为代入Naïve Bayes分类器的2个预报因子组合,进行小雨预报。贝叶斯最大后验准则通过比较两组后验概率(P(C1|x1,x2,…,x6),P(C1|y1,y2,…,y6))大小,决定哪组预报因子组合用来进行小雨预报,并将此组预报因子作为小雨预报的标签[19]。以第1组为例,根据贝叶斯定理,后验概率表示为
P(C1|x1,x2,…,x6)=P(x1,x2,…,x6|C1)·
P(C1)/P(x1,x2,…,x6)。
(1)
式(1)中,P(x1,x2,…,x6|C1)为预报因子组合(x1,x2,…,x6)在小雨中出现的条件概率,P(C1)为小雨的先验概率,P(x1,x2,…,x6)为(x1,x2,…,x6)都出现的概率。
Naïve Bayes假定预报因子之间相对于类别变量是条件独立的,每个预报因子只与类别变量相关联,所以条件概率又可表示为
(2)
则后验概率又可表示为
P(C1|x1,x2,…,x6)=
P(x1,x2,…,x6|C1)·P(C1)/
P(x1,x2,…,x6)=
(3)
其中,α=1/P(x1,x2,…,x6),是与小雨无关的参数。
2.2 遗传算法
遗传算法[20]模拟生物进化过程中的自然选择和遗传机制,形成一个具有生成和检验特征的搜索算法。它以种群为进化基础,以适应度函数为评价依据,通过种群中个体的遗传操作实现选择和遗传机制,建立起一个迭代过程。使新一代的基因(位串)集合优于老一代的基因集合,实现种群中个体的不断进化。遗传算法的基本流程如下:①根据问题确定基因位串,生成初始种群;②定义适应度函数,并计算所有个体的适应度;③确定遗传策略,运用选择、交叉和变异算子作用于群体,形成下一代新群体;④判断新群体性能是否满足要求,若不满足则返回步骤③,否则算法结束。
3 用遗传算法搜寻单站降水的Naïve Bayes预报模型的最优子集
3.1 遗传算法的初始化
3.1.1 确定基因位串和种群
为了从22个因子中搜寻4~6个因子组成Naïve Bayes模型的最优子集,采用二进制编码构建基因位串,入选模型的因子用“1”代表,否则用“0”代表,形成一个22位的二进制基因位串。每个基因位串代表1个个体,考虑到气象问题的特殊性,确定1个个体构成1个种群。同理,可以构造其他种群。遗传算法中,种群规模越大,个体越具有多样性,陷入局部收敛的危险就越小[21-22],但计算量会显著增加,而群体规模太小,搜索空间会受限制,故种群确定为30个。
3.1.2 定义适应度函数
降水预报模型的拟合结果,需要适应度函数进行评估。具体采用两种适应度函数:F1=N1/(N1+N3),其中,N1为对象发生时预报正确的次数,N3为对象发生时漏报的次数;F2=ST,即与TS评分一致。两种适应度函数评估后得到的模型分别称为GA-NB1和GA-NB2。
3.2 晴雨预报Naïve Bayes概率分类过程及遗传算法搜寻最优子集
将2008—2010年的6—9月的资料定为建模样本集,采用Naïve Bayes方法,构建单站13—24 h晴雨预报模型,并采用遗传算法搜寻预报模型的最优子集。
①计算先验概率。将单站相应时间的降水样本分为无(g=1,1代表无降水)和有(g=2,2代表有降水)两类,它们的先验概率f1和f2分别为
(4)
式(4)中,n1,n2分别是无雨和有雨的样本量。
②计算条件概率。分别将样本集中22个预报因子(X=[x1,x2,x3,…,x21,x22]),采用下式进行标准化。
g=1,2。
(5)
式(5)中,μk,g,σk,g分别是第k个预报因子在g类样本中平均值和均方差。
假定各预报因子服从正态分布,计算22个预报因子在降水有、无中的条件概率rk,1和rk,2。
(6)
③样本分类。在建模样本集中,随机构建30个个体基因位串,每个个体中为“1”的基因保持在4~6个,将这些个体基因位串,作为Naïve Bayes分类器的预报因子,依据式(3)建立判别方程组:
(7)
将前面得到的f1,f2,rk,g分别代入到式(7)中,得到判别值q1和q2(即降水有无的后验概率)。比较两者的大小,进而判别此次样本是否有降水发生。样本集中全部样本分类完毕,记为迭代1次。
④计算适应度函数及用遗传操作搜寻最优子集。第1次分类结束后,根据分类结果,分别计算适应度函数F1和F2。然后将随机得到的30个个体根据遗传算法进行择优运算,最终找到最优个体,即晴雨预报最优个体子集。遗传操作中,首先,采用算法轮盘赌策略选择父辈个体;然后,这些父辈个体两两配对,实现基因的交叉互换,得到子辈个体,交叉率为0.8;再将少部分子辈个体赋予全新的随机基因,实现变异操作,变异率为0.01;最后,重新计算子辈个体适应度,进入下一代遗传操作,循环往复,一直到适应度函数收敛或最大迭代步数(取50)为止。
每一代的遗传操作完成后,基因位串中会出现入选因子小于4或大于6的个体,这不符合入选因子为4~6个的要求。以基因位串中有7个因子的个体为例,需要剔除1个因子,采用以下步骤实施:依次剔除(将位串的1改为0)每一个因子,形成7个具有6个因子的基因位串个体;分别计算这7个个体的适应度,选择适应度最大的个体取代原个体;对基因位串中会入选因子小于4的个体,也要进行类似替换。
⑤测试分类。根据得到最优个体,选入构建Naïve Bayes分类器的预报因子,对测试集进行样本分类,获取晴雨预报结果,并记录测试集中降水发生的样本序号。
降水等级预报的Naïve Bayes概率分类过程除⑤测试分类外,其他部分与晴雨预报分类过程类似。在测试分类中,小雨预报模型对降水发生的样本进行预报,其他雨型预报模型中,排除已预报出的样本,对剩下晴雨预报有雨的样本进行预报。
3.3 试报和评分
当GA-NB1和GA-NB2的最优子集确定后,用于Naïve Bayes分类器的预报因子,然后用2011年6月27日—9月30日的90个样本(7月7日与7月13日样本缺失)作为测试集进行样本分类。类似地还可建立小雨、中雨、大雨和暴雨的预报模型。
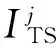
(8)
(9)
其中,N1为对象发生时预报正确的次数,N2为对象不发生时预报正确的次数,N3为对象发生时漏报的次数,N4为对象不发生时空报次数,j为降水分类级别。
4 最优子集分析和试报效果检验
4.1 最优子集分析
任何个体最优子集的适应度都具有前低后高的共性,以介休站晴雨预报为例,分析其最优子集的适应度值在遗传过程中的演变特点。图1给出了介休站GA-NB1和GA-NB2晴雨预报模型拟合适应度曲线。GA-NB1的适应度函数为F1,用实线表示,其含义类似于准确率,但未考虑天晴并报对的情况。
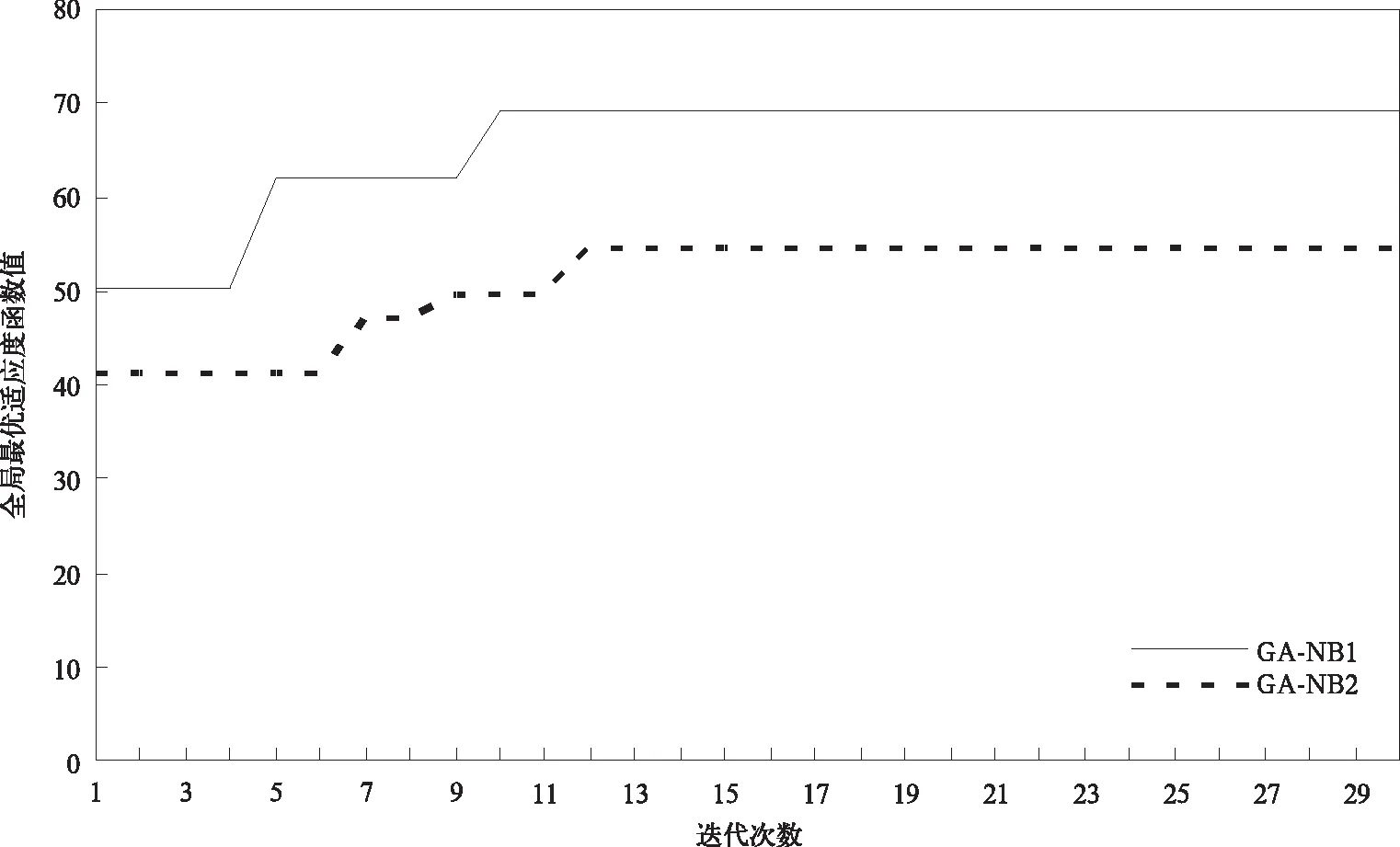
图1 介休站晴雨预报GA-NB1与GA-NB2拟合适应度曲线Fig.1 The simulated precipitation occurrence prediction fitness functions of GA-NB1 and GA-NB2 at Jiexiu Station
GA-NB2的适应度函数为F2,与TS评分的含义一致,用虚线表示。由图1可以看出,第12步迭代后,两种适应度函数进入收敛状态,分别是0.692和0.544。GA-NB1的适应度函数值在第10步后进入收敛状态,由初始的0.50,提升到0.69,升幅约0.19。GA-NB2的适应度函数值在第12步后进入收敛状态,由初始的0.42提升到0.54,升幅约0.12。可见最优子集的Naïve Bayes模型拟合效果,比普通子集有较大提高。
表1给出了介休站GA-NB1和GA-NB2晴雨预报模型的最优子集中因子的构成情况。由表1可见,两个子集的主因子为模式输出的降水量,属于强制入选,这样在MOS原理下,可消除模式的系统性误差,其余共同的因子为地面温度、温度露点差和假相当位温。两子集因子数均为6个,反映了对于该站该时次,用2~4个因子纠正模式输出的降水量,尚不能形成最优子集。

表1 介休站根据两种适应度函数GA选出的晴雨预报因子最优组合Table 1 The best optimal subsets of precipitation occurrence predictors selectedby two kinds of fitness functions at Jiexiu Station
4.2 试报效果检验
图2给出了GA-NB1模型对介休站2011年7—9月13~24 h(即次日08:00—20:00)的预报结果,并与模式输出及实况进行对比,图2中对于实际无雨且两种预报方法均预报无雨的样本,给予剔除。由图2可以看出,GA-NB1显著减少了T511模式小雨的空报次数,共减少24次,对中雨的空报次数也有一定减少,GA-NB1预报8次正确5次,T511预报11次,正确3次,对大雨和暴雨的预报,由于样本太少,具有偶然性,不能说明问题。
从上面的结果还可知,T511模式的预报效果要明显低于GA-NB1模型,其主要原因在于评分方式不一样。数值预报降水TS评分方法为若预报某区域某时次有雨时,以该区域的格点为中心,以适当的半径进行扫描,若扫描半径内有1个测站观测有雨,则预报正确,否则预报错误。显然,数值预报侧重于区域降水预报结果,允许有一定的扫描半径。而本试验基于单站展开,为了比较预报效果提高情况,需要对T511模式降水预报采用单站评分方式。因此,T511模式降水预报单站评分可能不高,不代表其区域降水评分不好。

图2 2011年7—9月介休站GA-NB1模型13~24 h的降水分级预报结果Fig.2 The observed, GA-NB1 and T511 predicted 13-24-hour classificatory precipitation at Jiexiu Station from Jul to Sep in 2011
表2给出了介休、运城、丰宁3个站2011年7—9月13~24 h的预报结果。由表2可见,两种GA-NB模型预报结果均好于T511模式。其中,晴雨预报:GA-NB1模型3个站预报准确率平均为87.40%,最高为介休站和丰宁站(90.0%),最低为运城站(82.2%);GA-NB2模型3个站预报准确率平均为86.30%,最高为介休站(90.0%),最低为运城站(81.1%),GA-NB1模型预报准确率平均值略高于GA-NB2模型;T511模式3个站预报准确率平均为67.03%,最高为丰宁站(78.9%),最低为运城站(57.8%),T511模式平均预报准确率明显低于GA-NB1和GA-NB2模型。小雨预报:GA-NB1模型3个站TS评分平均为0.410,GA-NB2模型TS评分为0.367,T511模式预报TS评分为0.207,可见两种GA-NB模型比T511模式提高了0.16以上。中雨预报:GA-NB1模型3个站TS评分平均为0.443,GA-NB2模型为0.267,T511模式预报为0.143, GA-NB1模型效果好于GA-NB2模型和 T511模式。大雨和暴雨的预报因样本过少,不做评述。

表2 介休站、运城站、丰宁站2011年7—9月13~24 h降水分级预报结果Table 2 The prediction evaluation of 13-24-hour classificatory precipitation at Jiexiu, Yuncheng and Fengning stations from Jul to Sep in 2011
从上面的试验结果可知:GA-NB模型可显著提升晴雨预报的准确率和小雨、中雨的TS评分,且GA-NB1模型好于GA-NB2模型。以下从漏报和空报的角度,分析GA-NB模型效果提升的原因。晴雨预报GA-NB1模型、GA-NB2模型和T511模式3个站平均正确次数分别为17.0,16.7,19.3,漏报次数分别为4.3,4.7,2.0,空报次数分别为8.0,8.0,27.7。其中,T511模式预报正确次数最多,漏报最少,空报最多,GA-NB模型与T511模式相比,正确次数略降(GA-NB1模型,GA-NB2模型平均降2.3)和漏报次数略升(平均升2.7),而空报次数有显著下降(平均降19.7)。因此,GA-NB模型提升晴雨预报准确率的原因在于能有效降低模式的空报率。小雨预报GA-NB1模型、GA-NB2模型和T511模式3站平均正确次数分别为9.0,8.7,8.0,漏报次数分别为6.0,6.3,7.0,空报次数分别为7.0,9.0,24.7。也能得到与晴雨预报类似的结论。中雨预报则不同,GA-NB1模型、GA-NB2模型和T511模式3站平均正确次数分别为3.7,2.7,2.0,漏报次数分别为1.3,2.7,3.0,空报次数分别为3.7,8.7,2.3。可见,GA-NB模型比模式正确率略微提升,漏报略降,空报率反而升高。
5 结论与讨论
为了搜寻Naïve Bayes降水概率预报模型的最优子集,利用2008—2010年T511数值预报产品和单站观测资料,采用遗传算法,对介休、运城、丰宁3个站Naïve Bayes降水概率13~24 h分级预报模型进行研究,提出了遗传算法搜寻Naïve Bayes模型最优子集的方案,得到GA-NB1和GA-NB2两种不同适应度函数的最优子集模型,并利用2011年7—9月的资料,对模型效果进行检验。结论如下:
1) 最优子集的拟合效果明显高于普通初始子集。以介休站为例,在所有子集中规定数值模式输出降水量因子必须入选的情况下,GA-NB1模型的适应度函数初始值为0.50,收敛值为0.692,升幅约0.19;GA-NB2模型的适应度函数初始值为0.42,收敛值为0.54,升幅约0.12。
2) 最优子集模型能够显著提高数值模式在单站的预报效果。GA-NB1模型、GA-NB2模型和T511模式3个站平均晴雨预报准确率分别为87.40%,86.30%,67.03%,小雨预报TS评分分别为0.410,0.367,0.207,中雨预报TS评分分别为0.443,0.267,0.143。两种模型晴雨预报准确率比T511模式提高了19%以上,小雨、中雨预报TS评分分别提高了0.16和0.13以上。GA-NB1模型效果好于GA-NB2模型。
3) 最优子集模型对晴雨、小雨预报效果提高原因是有效降低了数值模式的空报率,3个站空报次数,GA-NB1模型和GA-NB2模型比T511模式均降低了19次以上。而最优子集模型对中雨预报效果提高原因,是能够小幅提高正确次数和降低空报次数。
采用遗传算法求Naïve Bayes模型的最优子集要花费较长时间建模,利用主频2.4 GHz以上微机1次计算时间约为15 s,远低于建1次穷尽所有组合的最优子集所需的时间。从理论上讲,遗传算法还可应用于多数其他方法(不具备最优子集算法体系的方法),具有一定的推广性。本文利用华北雨季(6—9月)资料研究大雨和暴雨预报效果,个例数偏少,有待于积累更长的试报样本进行检验。
[1] 闵晶晶,孙景荣,刘还珠,等.一种改进的BP算法及在降水预报中的应用.应用气象学报,2010,21(1):55-62.
[2] 刘还珠,赵声蓉,陆志善,等.国家气象中心气象要素的客观预报——MOS系统.应用气象学报,2004,15(2):181-191.
[3] 刘爱鸣,潘宁,邹燕,等.福建前汛期区域暴雨客观预报模型研究.应用气象学报,2003,14(4):420-429.
[4] 赵声蓉,裴海瑛.客观定量预报中降水的预处理.应用气象学报,2007,18(1):21-28.
[5] 燕东渭,孙田文,杨艳,等.支持向量机数据描述在西北暴雨预报中的应用试验.应用气象学报,2007,18(5):676-681.
[6] Raftery A E,Gneiting T,Balandaoui F,et al.Using Bayesian model averaging to calibrate forecast ensembles.MonWeaRev,2005,133:1155-1174.
[7] Sloughter J M,Raftery A E,Gneiting T,et al.Probabilistic quantitative precipitation forecasting using Bayesian model averaging.MonWeaRev,2007,135:3209-3220.
[8] Liu J N K,Li B N L,Dillon T S.An improved Naive Bayesian classifier technique coupled with a novel input solution method.IEEETransactiononSystem,Man,andCybernetics-PartC:ApplicationandReviews,2001,31(2):249-256.
[9] 王开宇,赵瑞星,翟宇梅.朴素贝叶斯分类器在降水预报中的应用.军事气象水文,2007,31(3):41-44.
[10] 郭雅芬,过仲阳,苏君毅,等.贝叶斯分类法在MCS移动路径预测中的应用.地球信息科学,2007,9(2):20-23.
[11] 苏君毅,邱洁,过仲阳,等.基于贝叶斯方法的中尺度对流系统移动方向研究.华东师范大学学报:自然科学版,2006,6:41-46.
[12] 柯宗建,张培群,董文杰,等.最优子集回归方法在季节气候预测中的应用.大气科学,2009,33(5):994-1002.
[13] 谷德军,纪忠萍,李春晖.南海夏季风爆发日期与海温的多尺度关系及最优子集回归预测.海洋学报,2011,33(6):55-63.
[14] 李玲萍,尚可政,钱莉,等.最优子集回归在夏季高温极值预报中的应用,兰州大学学报:自然科学版,2010,46(6):54-58.
[15] Nawaz M,Enscore E,Ham I.A Heuristic algorithm for the machine,n job flowshop.TheInternationalJournalofManagementSciences,1983,11(1):91-95.
[16] 赵凯,孙燕,张备,等.T213数值预报产品在本地降水预报中的释用.气象科学,2008,28(2):217-220.
[17] 刘建文,郭虎,李耀东,等.天气分析预报物理量计算基础.北京:气象出版社,2005:1-253.
[18] 王学忠,胡邦辉,吕梅,等.沙瓦特指数的一种迭代算法.应用气象学报,2009,20(4):486-491.
[19] Zhou Lina,Feng Jinjuan,Sears A,et al.Applying the Naïve Bayes Classifier to Assist Users in Detecting Speech Recognition Errors.Big land,Hawaii:System Sciences,Proceedings of the 38th Annual Hawaii International Conference,2005:183.
[20] 韩瑞峰.遗传算法原理与应用实例.北京:兵器工业出版社,2010:1-443.
[21] 夏祥华,孙汉文.基于遗传算法的曲线拟合方法用于重叠荧光光谱的定量解析.光谱学与光谱分析,2012,32(8):2157-2161.
[22] 王双成.贝叶斯网络学习、推理与应用.上海:立信会计出版社,2010:1-291.
An Algorithm of Optimal Subset for Bayes Precipitation Probability Prediction Model
Hu Banghui1)Liu Shanliang2)Xi Yan3)Wang Xuezhong1)You Daming1)Zhang Huijun3)
1)(InstituteofMeteorologyandOceanography,PLAUST,Nanjing211101)2)(UnitNo. 61741ofPLA,Beijing100081)3)(MeteorologicalandHydrologicalCenterofMilitaryAreaCommandofNanjing,Nanjing210016)
Based on numerical prediction products, a model output statistic (MOS) for precipitation forecast of an observatory is set up which contains the model output rainfall as one of predictors. The model can remove the systemic error of numerical prediction on precipitation, so it improves the precipitation prediction skill to certain degree. But for a given amount of predictors, a problem to solve is how to select the optimal subset to improve the prediction skill especially in operational weather forecast. In order to construct a Naïve Bayes precipitation probability prediction model on the precondition of the best performance from optimal subsets, using T511 model products and their 13-hour to 24-hour forecast corresponding observation of precipitation from 2008 to 2010 at three observatories, namely Jiexiu, Yuncheng and Fengning, the classificatory Naïve Bayes models on precipitation probability are developed and valuated. Different from the treatment of classic optimal subsets regression which enumerates the optimal subset one by one under the rule of couple score criterion (CSC), a Naïve Bayes model using genetic algorithm to search the optimal subset from a great many of subsets is presented. Model follows artificial intelligence searching characteristics. The genetic algorithm is established through the construction of gene bit-series from binary encoding method, and the introduction of a fitness function with cause. Considering the elimination of non-existing affair samples for the weather of low probability, two models are built based on genetic algorithm and Naïve Bayes model. The essential difference between two kinds of models is the fitness functions they use: One uses the accuracy of precipitation as fitness function, and it is called genetic algorithm-Naïve Bayes forecasting model type 1, GA-NB1 in brief; the other one uses threat score as fitness function, and is called GA-NB2 accordingly. The models are evaluated by prediction tests with dataset ranging from July to September in 2011. Results indicate that simulated results of optimal subset are much superior to those of ordinary initial subsets. Both GA-NB1 and GA-NB2 can improve T511 model precipitation accuracy by 19% on precipitation occurrence, threat scores are improved by 0.16 and 0.13 on drizzle and moderate precipitation, respectively. The prediction for precipitation occurrence and drizzle is enhanced by the optimal subset model because they effectively reduce the false alarm rate of numerical model, by more than 19 times during the period. The cause for improving moderate rain prediction includes two aspects: A slight increase in the amount of correct forecast and decrease of false alarms.
genetic algorithm; Naïve Bayes classifier; station precipitation forecast; prediction skill
国家自然科学基金项目(41330420,41275099)
2014-08-31收到, 2015-01-04收到再改稿。
* email: hubanghui@126.com
